考虑设备可靠性的自动生产线性能分析

张蓝天，张雨琦

（西南科技大学 制造科学与工程学院，四川 绵阳 621010）

0 引言

现代制造环境中，制造企业面临着越来越多的挑战，要以更灵活的自动化生产线、更短的交付周期和更低的成本向客户提供各式各样的产品，而制造过程中会受到设备故障等因素的影响。企业应结合设备可靠性来分析生产线的性能，这对于调整生产计划、提升自动化制造过程生产效率具有重要意义。

随着制造业大力发展，相关学者对制造企业及自动化生产线相关问题进行了大量研究。宋科，等采用可编程逻辑控制器，设计了大型通讯柜自动化包装生产线。李娜，等建立了两环闭型排队网络模型，并采用分解迭代算法分析芯片制造封装生产线的生产率。邓兰兵通过EM-Plant仿真建模工具对变速箱齿轮加工自动生产线进行了性能分析，并研究了缓存区设置对自动化生产线生产率的影响规律。为了提高制造系统的性能，自动化生产过程中的各种参数需要进行合理的配置。Smith，等研究了有限缓冲区和指数加工时间的排队网络稳态性能分析。Meng Gang，等建立了开放排队网络模型，研究批量大小对无限缓冲区的影响。在制造系统排队网络模型中，Tancrez，等采用分解迭代方法研究了有限缓冲对装配生产线性能的影响。针对制造系统如数控机床和生产线的随机干扰问题，杨林，等考虑设备故障桥梁支座生产线的缓冲库存进行设计；高俏俏基于部件故障提出串联系统预防性维修策略。现有研究同时考虑实际自动生产过程中设备可靠性和不同产品生产设备刀具切换对制造系统性能影响的较少。

本文重点提出了考虑设备故障的多产品自动生产线排队模型，并运用Tecnomatix Plant Simulation 仿真软件分析系统的各项性能指标。讨论了设备可靠性等干扰因素在生产线关键参数变动下对性能指标的影响，为寻找性能的改进方向提供参考。

1 问题描述和模型假设

1.1 系统问题描述

通常设定生产系统为由一组工作站和缓存区组成的多阶段生产线，如图1所示。根据文献和实际的调研，D厂自动装配生产线可同时生产三类产品（P1-P3），每类产品根据各自的工艺路线进行加工和检测，如图2所示。

图1 串联式的生产系统

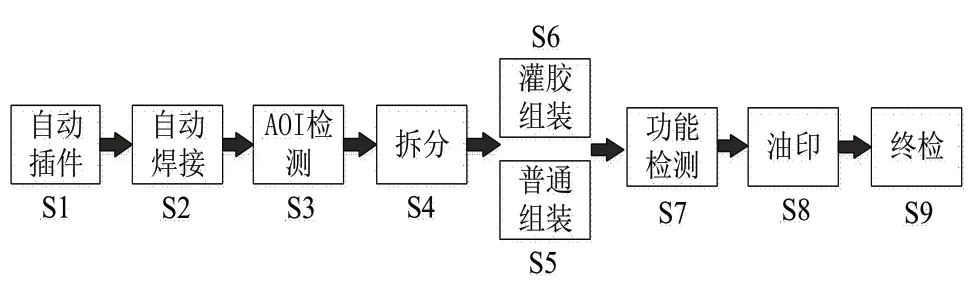
图2 自动装配生产线工艺流程

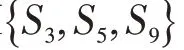
1.2 问题假设

根据马尔科夫理论，串联式生产系统可以分解为多个独立的连续时间马尔科夫链（CTMC），求解排队网络稳态概率问题，多产品单个工作站模型如图3所示。其中自动化生产线中各工位加工能力不同，缓存区容量有限且含多个并行设备。

图3 多产品单工作站模型

（3）每个工作站的机器均能生产m种产品，任意时刻机器只生产一个产品。

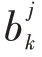
图4 存在返工的流动结构

1.3 各工位排队模型描述

某自动装配生产线的排队模型描述如下：

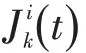
（2）三种产品进入检测工位中不需要刀具切换，直接进行检测。根据实际数据显示该工位常出现故障，且远大于加工工位的故障率，因此考虑了检测工位h中设备平均故障率ξ和平均修复率η对检测工作站的性能影响。

2 各工位模型构建及求解

2.1 各工位状态空间分解模型

结合自动装配生产线的描述，各工位的输入速率、流出速率等参数可被用作推导其他工位马尔科夫过程状态转移平衡方程。求解出各工位的状态概率，进而求得整个生产线的评价指标。

图5 加工工位的状态转移

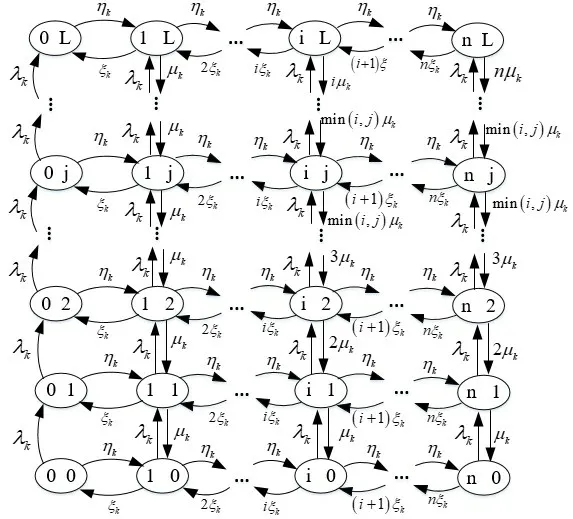
图6 检测工位的状态转移

根据状态转移图可列出插件工位和检测工位的状态转移平衡方程组，由方程系数组成稀疏矩阵，应用文献[13]和[14]中提出的迭代方法可求出加工工位和检测工位各状态的稳态概率。其中迭代过程的收敛性证明可参考文献[14]。

2.2 排队模型参数的修正

求解上述状态稳定概率时，各工位的服务率和产品到达率与实际生产过程存在区别，所以需要对各转移方程中相关参数进行修正。

（1）加工变动性。实际加工工位的设备同样存在可靠性δ，会对加工速率带来干扰，加工工作站k在生产i 产品时实际有效加工速率可重新等效，见式（1）。

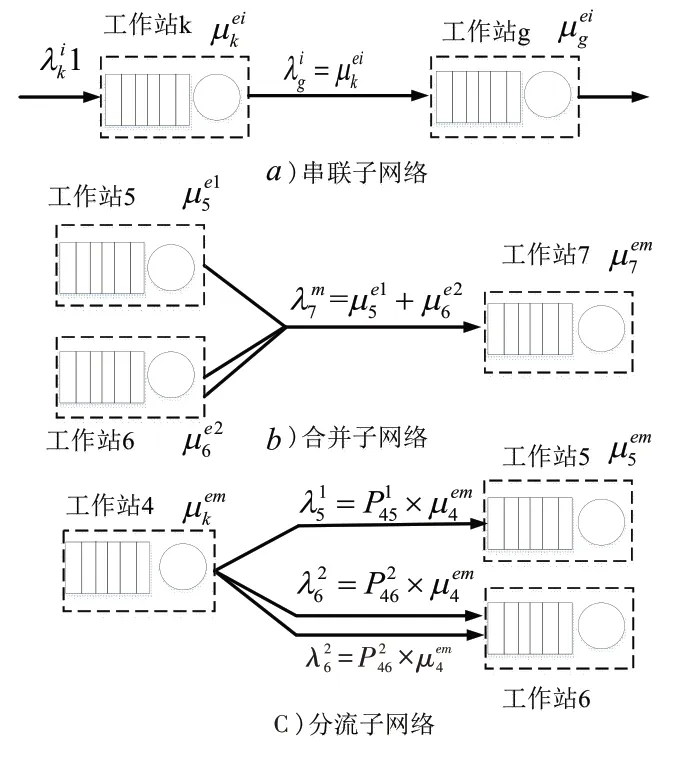
图7 工位流动结构

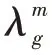
2.3 模型评价指标

两类工作站5个评价指标如下，并作为仿真统计分析的指标：

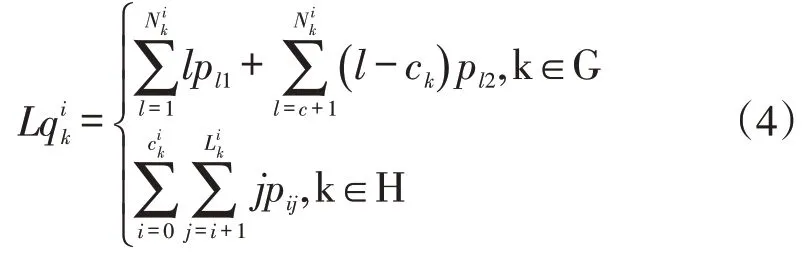
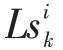
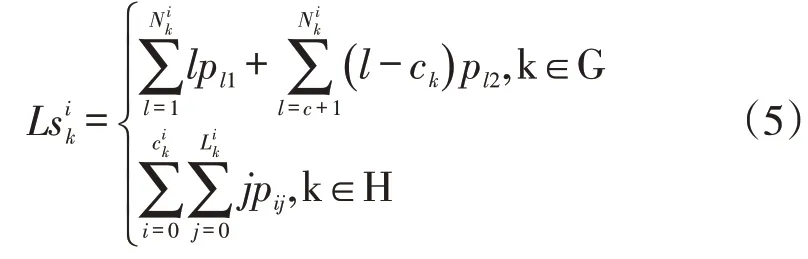
（4）工作站k在单位时间内生产产品i的平均生产件数，即生产率，记为Tp，有：

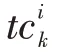
生产系统的评价指标如下：

（1）产品i总的生产周期记为TC。实际工作站生产完该工序后，产品以一定批量离开该工作站，工件生产周期中应考虑成批时间：

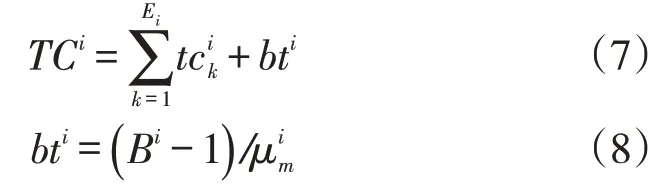
其中，bt表示产品i等待成批时间，B是产品i的加工批量大小。

（2）单位时间内产品i在生产系统中的吞吐量记为WIP：

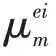
3 实例验证与分析

3.1 模型参数设置

以生产3种电源适配器的某企业生产线为例进行数值分析和仿真模型对比，验证模型的有效性和数值的准确性。数值分析采用MATLAB2014a，计算机性能为i5-5200的中央处理器，2.20GHz、8.00GB内存，64位Win10操作系统。

本文收集并整理了实际生产线的历史加工时间，各设备历史故障修复数据和各产品在检测站中的合格率等数据。表1为考虑实际变动的每类产品在各工作站的参数，包含服务率（服从负指数分布）和缓存区容量b，各产品在自动插件工位S1 的初始投放率，即到达率均为2，服从泊松分布。然后对构建好的对应的Tecnomatix Plant Simulation 仿真模型设置仿真逻辑并进行参数输入，进行仿真模拟运行。

表1 各工位的初始参数

为确保仿真试验结果的有效性，经测验采取120min 仿真预热时间，重复运行20 次仿真模拟并设置95%的置信区间，每个性能指标标准偏差在平均值的05%以内。

3.2 实验结果对比与分析

基于Plant Simulation 仿真平台建立生产线仿真模型，让实体通过静态过程来收集所需的数据，最后，构造统计估计器计算样本的结果，获得每个工作站和检测站仿真模拟的性能指标结果，部分实验结果见表2和表3。

表2 加工工位的实验结果对比

表3 检测工位的性能指标实验结果对比

其中仿真分析具体的性能指标包括工作站的机器负载率、排队队长、平均队长、生产率以及工作站平均生产周期。

除此之外，计算了该方法的仿真模拟结果和近似方法结果之间的相对误差△。

根据表2，采用近似方法求解3 类产品在工站中的5个性能指标计算值和仿真模拟值的最大相对误差分别是3.15%、3.88%、4.59%、3.48%和2.17%。拆分工位S4生产率最大，组装工位S6的生产周期长。检测站中的5个性能指标计算值和仿真模拟的相对误差见表4，其中功能检测工位生产周期和排队队长均为最长，可以作为观测重点。

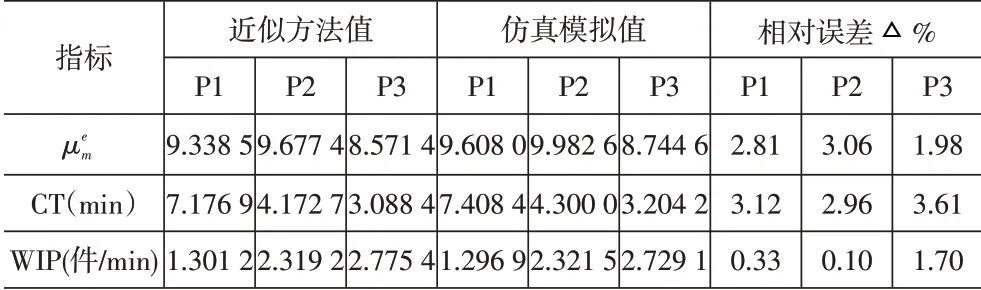
表4 生产线性能指标对比

对于生产系统性能指标的验证，与仿真模型相比，CT最大的相对误差为3.61%，见表3。各个工作站和检测站平均生产率估计值的相对误差均未超过2.6%，所提出的近似模型对平均生产率具有较好的估计。其中产品1的生产周期最大，产品3单位时间的生产量最大。

除在初始参数上分析性能指标，还分析了服务率变动对自动化生产线生产周期的影响。如图8所示，三类产品总的生产周期CT 随服务率变动系数-变化的曲线图，并和仿真模拟进行对比。式（11）中，σ表示变化后的服务率与原始服务率ˉ间的标准差。

如图8 所示，当-07，三类产品的生产周期对-的增加越敏感，产品1 的生产周期对-的波动更敏感。产品1的机器服务率与其他类型产品比较，较小的生产周期受到-的影响会更加明显。干扰因素对轻微的变化，生产周期未有明显的波动。所以可认为设备故障率和修复率在一定范围值下，对生产周期的影响属于正常的波动，另外改善各工位的服务率也不是总能使生产线性能改善。

图8 生产周期CT随CV-μ 的变化

3.3 灵敏度分析

本部分主要分析系统参数变动会对各工位的评价指标带来怎样影响。首先分析了缓存区容量b变化对工位性能影响，以自动焊接工位为例，初始b为2，各类产品到达率和服务率见表1。如图9所示，当b增加，工位中排队队长和平均生产周期呈线性的增长。当工位增加一倍时，各类产品同比减小。当缓存区容量b在2-10范围增大，生产率上升，阻塞率P迅速下降，即焊接工位b为10时性能指标趋于稳定。因此，合理配置缓存容量能有效改善生产速率，缓解生产线的阻塞。

图9 缓存区容量b对工作站性能的影响

以拆分工位为例，三类产品在两种不同的加工服务率下到达率变动-对工位性能的影响，如图10所示。平均队长和阻塞率P随到达率的变动系数增加而增长。-为0.3 时是平均队长曲线的拐点。三类产品平均生产周期tc影响较小，而对比减小的情形下，tc受到-的变动影响越明显；当-为0.4，tc趋于稳定。平均生产率随着-的增加，其增长趋势较小，同时变化对增长的敏感度没有变化。因此，调整服务率能有效改善到达率的变动对拆分工位生产周期的影响。

图10 到达率变动CV-λ 对工作站性能的影响

以AOI 检测工位为例，服务率的变动系数-对工位性能的敏感度，如图11所示。-为0.6时是平均队长、机器负荷率、生产率和空闲率P4条曲线的拐点，当-06 时，和逐渐下降，和P逐渐增加，且在0.6 以后，变化对AOI检测工位评价指标的影响不断增大。可以得出缓存区容量、到达率和服务率的变动中，服务率是影响生产系统性能波动最敏感的参数。因此，生产过程中要时刻关注机器的可靠性以及干扰因素对各工位机器服务率的影响。

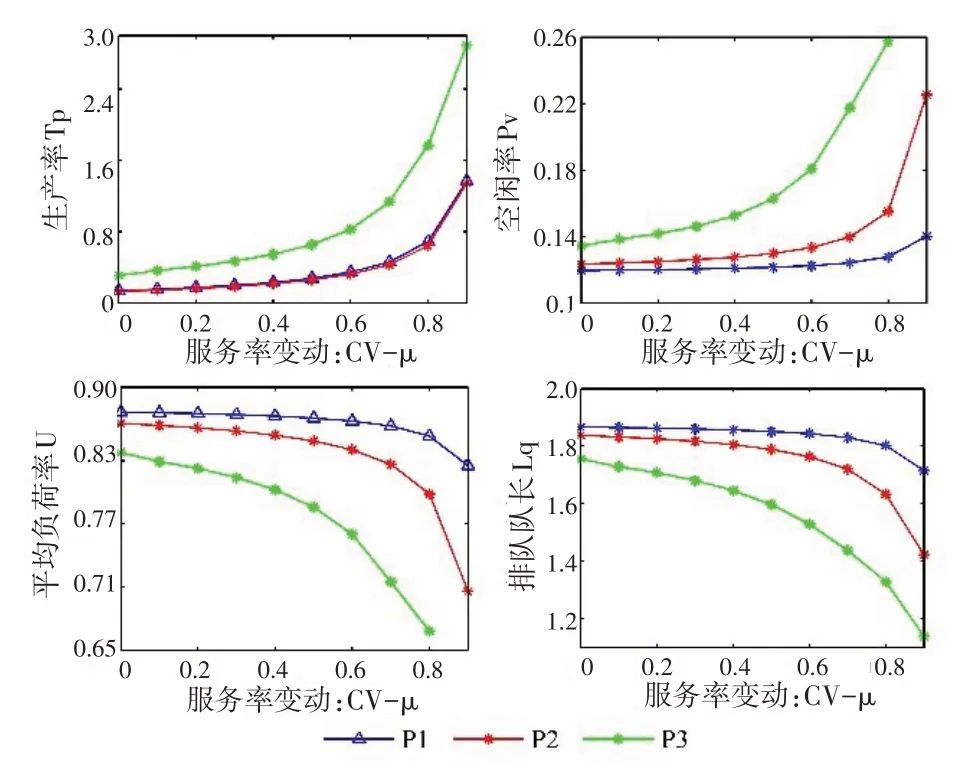
图11 服务率变动CV-μ 对工作站性能影响

4 结论

本文针对具有有限缓存区和设备故障率的自动化生产线，运用排队模型对不同情况的工位建立生产系统的性能分析模型，并对各工位和生产线进行多个评价指标分析，借助仿真软件模拟仿真。以某车间实际生产数据为例，验证所提近似模型对性能分析的有效性。最后考虑对机器服务强度和到达率的约束，分析工位和生产线性能受关键参数变动的敏感度。

本文对D厂自动化生产系统的参数进行讨论为决策者优化生产线、提高生产效率提供了理论依据。为了让该模型更加符合真实车间的情况，未来还可以研究紧急插单、运输问题以及更复杂的工艺路径的系统。