基于应变的柔性飞机刚弹耦合建模方法研究

杨建忠，卢 勇，杨士斌

（中国民航大学适航学院，天津 300300）

飞机舒适性、机动性等性能的提高及生产和使用成本的降低使得飞机结构的相对重量更轻，表现出越来越高的柔性，从而降低了弹性模态的频率[1-3]。 因此，飞机刚体运动与气动弹性响应之间会出现耦合，导致柔性飞机受气动力的影响与刚体飞机不同，如果按照传统刚体假设去设计飞行控制，可能会与真实飞行有较大差异，甚至产生不利影响危及飞机的正常飞行，因此必须考虑刚体和弹性体耦合的飞行动力学模型。

在建立飞机刚弹耦合模型时，大多基于机翼进行小变形假设：Waszak 等[4]采用平均轴系法将刚体飞行动力学与线性结构动力学耦合，将弹性和刚性自由度解耦，使两者之间的耦合仅通过广义力产生；Meirovitch 等[5-6]采用模态分支法将飞机视为由多个弹性体构成，刚体运动由飞机重心所在体轴系描述，弹性运动则由各弹性体建立与其固连的各参考系之间的运动关系表示。平均轴系法与模态分支法的结构动力学都是线性的，因此，当机翼等弹性结构存在较为明显的变形时，用这些方法分析飞机的运动是不适用的。

当机翼作大变形运动时，可以将机翼视为非线性梁，用非线性结构动力学来描述运动。绝大多数非线性梁模型分为3 种：本征梁模型[7-9]、基于位移的非线性梁模型[10]、基于应变的非线性梁模型[11-13]。 由于这3种模型选用的自变量不同导致各有不同的优缺点。 本征梁模型自变量个数过多，基于位移的非线性梁模型建模过程较为繁琐且收敛较慢，而基于应变的非线性梁模型虽然未知数求解量较多，但具有较低的阶数。

目前，非线性梁模型主要运用于高空长航时无人机建模，而用该模型建立民用运输类飞机刚弹耦合模型的研究较少。本研究采用基于应变的非线性梁模型建立民用运输类飞机的刚弹耦合模型；通过研究从刚体到刚弹耦合模型的转换获得与飞行动力学有关的等效参数；基于大变形的刚弹耦合模型与刚体模型响应的差异采用非线性动态过程的时域仿真进行分析。该方法可应用于大柔性飞机的飞行控制设计。

1 大变形机翼飞机运动方程

1.1 基于应变的非线性梁模型

基于应变的非线性梁模型考虑了惯性坐标系（G）、机体坐标系（B）、局部坐标系（w）和辅助坐标系（b），如图1 所示。 惯性坐标系用于定义飞机相对于地球的位置；机体坐标系用于定义飞机刚体的自由度；局部坐标系用于定义梁每个节点的位置和方向；辅助坐标系用于定义连接到梁上的刚性单元的位置和方向，如连接到机翼上的发动机。 需要注意各坐标系轴的定义与研究传统刚体飞机的不同，如机体坐标系中Bx垂直于机身对称轴线指向右，By沿机身对称轴线指向前，Bz根据右手螺旋定则定义。

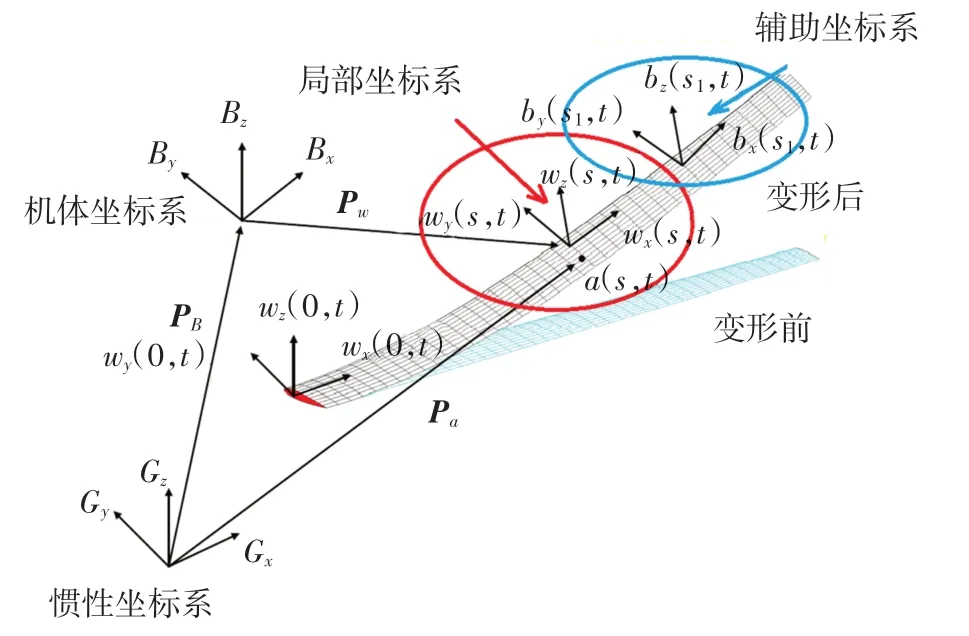
图1 坐标系统Fig.1 Coordinate system

根据该坐标系统，飞机的运动可以表示为

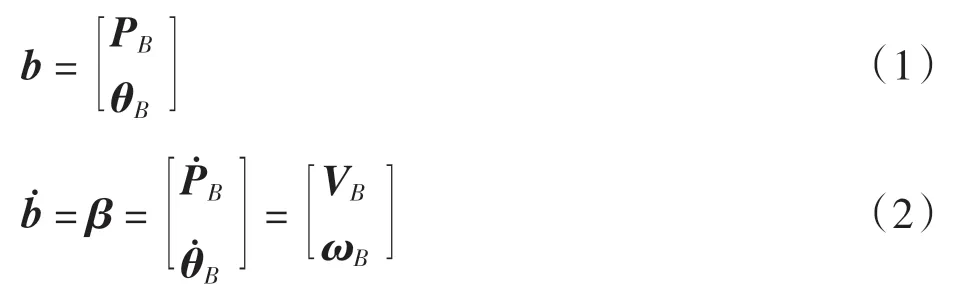
式中：b 表示惯性坐标系下的广义位移；PB、θB表示机体坐标系相对于惯性坐标系的位置和方向；表示b对时间求导，可得机体坐标系的速度β，再对时间求导，可得加速度；VB=[U V W]T表示Bx、By、Bz轴方向上的速度；ωB= [P Q R]T表示绕Bx、By、Bz轴转动的角速度。

基于应变的非线性梁理论中结构变形用应变表示为

式中：εx是梁单元中沿着梁展向的变形；κx、κy、κz分别表示梁单元相对于局部坐标系中wx、wy、wz轴的扭转。

在图1 坐标系统中Pw表示局部坐标系相对于机体坐标系的位置，局部坐标系相对于惯性坐标系的位移Pa表示为

由式（5）可以得到梁单元中s 节点t 时刻位置和的方向矢量表示

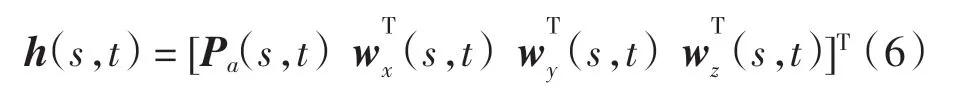
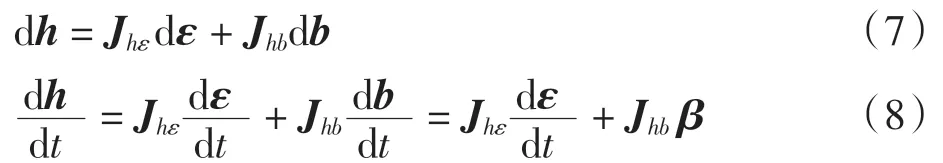
1.2 刚弹耦合模型的运动方程

根据虚功原理，飞机内力产生的虚功和外力产生的虚功之和为0。 通过计算内、外虚功，可以推导出刚弹耦合模型的运动方程表示为

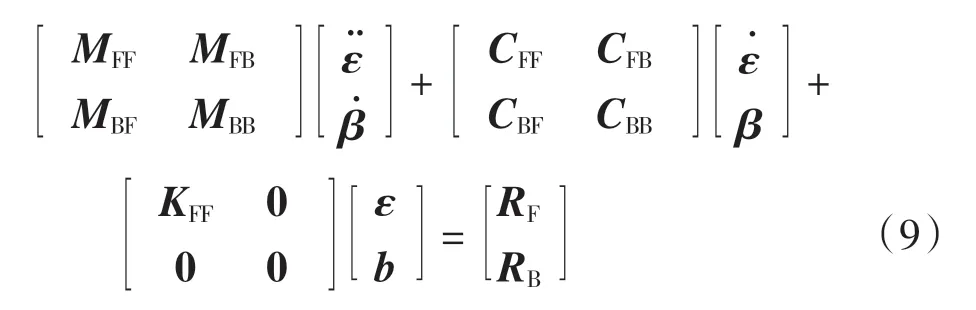
式中：MFF、MFB、MBF、MBB表示广义质量矩阵的子矩阵；CFF、CFB、CBF、CBB表示广义阻尼矩阵的子矩阵；KFF表示结构刚度矩阵；RF和RB表示广义力，通过计算施加到每个结构节点的气动力，可以获得重力和发动机推力。由于广义质量矩阵不是对角阵，可以看到飞机刚体运动β 与结构弹性运动ε 存在惯性耦合。

方程（9）中等号左边的子矩阵为

式中：M 表示弹性结构质量矩阵，其仅取决于弹性结构的惯性和质量而不取决于应变；MRB表示广义刚体机身质量矩阵，其取决于刚体机身惯性和质量；C 表示结构阻尼矩阵，此处，C=ζKFF，ζ 为阻尼比；CRB是广义刚体机身阻尼矩阵，取决于刚体机身质量和角速度；Hhb是以ωB的叉乘矩阵为子矩阵的对角矩阵与Jhb相乘的矩阵。

方程（9）中的广义力表示为

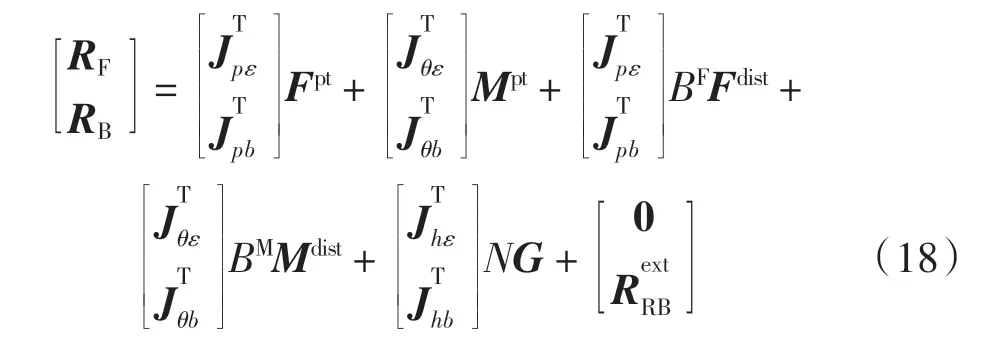
式中：Fpt、Mpt表示点力和点力矩；BF、BM、N 表示影响系数，由数值积分得到；Fdist、Mdist表示分布力和分布力矩；G 表示重力；表示广义外力， 由作用于刚体机身的外力和外力矩组成。

描述柔性飞机的运动学方程为

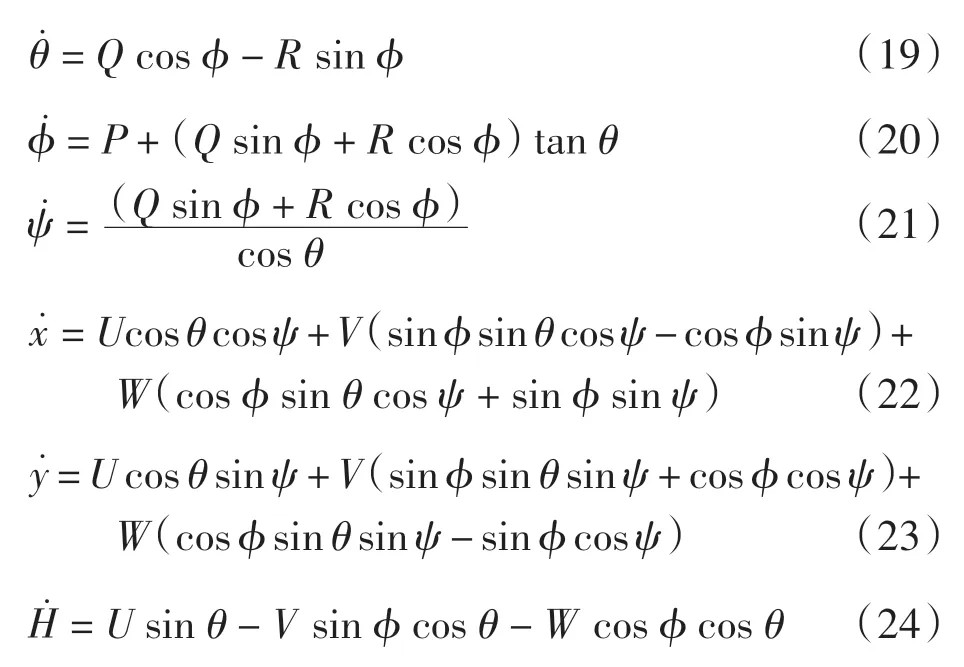
式中：θ、φ、ψ 分别表示飞机的俯仰角、滚转角、偏航角；x、y、H 表示惯性坐标系中飞机3 个方向的位移。

2 飞机模型参数

2.1 飞机几何参数

原始飞机几何数据来源于Silva[14]的研究。Silva 提出的柔性飞行器模型有3 种，飞机几何数据选择的是第1 种模型Conf1。由于在刚弹耦合模型和刚体模型之间的比较侧重于飞机的刚体运动，Conf1 模型可以方便地对具有适度结构柔性的飞机进行建模和分析。如果使用具有更高结构柔性的另外两种飞机模型，其柔性可能会显著影响飞机的操纵性和稳定性，导致飞机刚体运动受到严重影响。Conf1 模型中飞机长33 m，机身截面半径1.5 m，弹性部件几何参数如表1 所示。飞机视图如图2 所示。

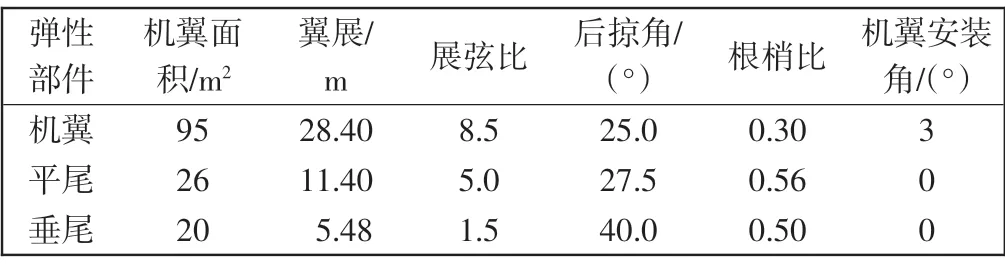
表1 弹性部件几何参数Tab.1 Geometric parameters of elastic components

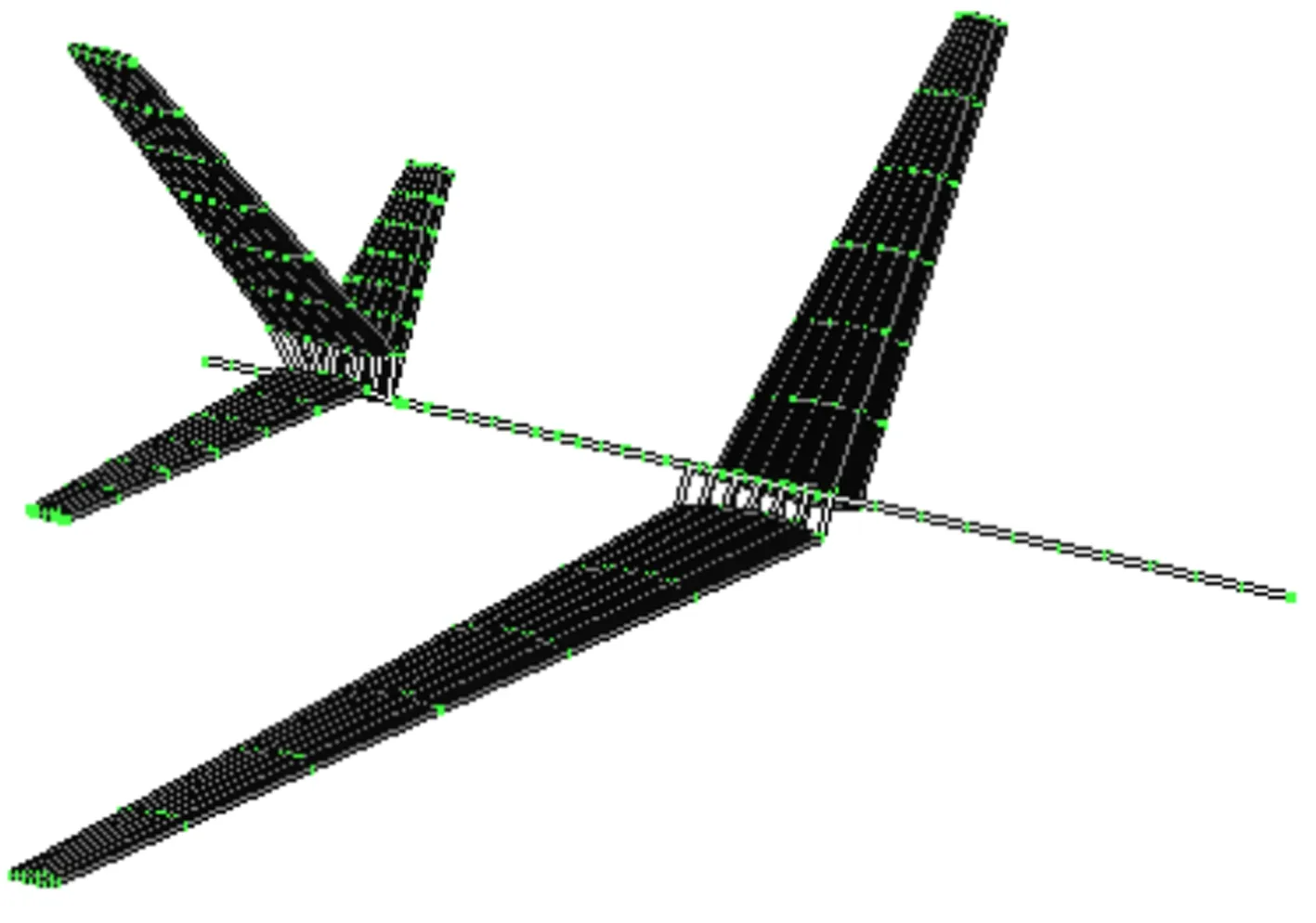
图2 飞机视图Fig.2 View of aircraft

2.2 飞机气动参数分布

为了便于计算，选择准定常气动力模型计算飞机受到的气动力载荷。 机翼剖面如图3 所示，图中b 为机翼半弦长，d 为机翼的气动轴系统到翼弦中点的距离。为速度V 的分量，L 表示升力，D 表示阻力，M表示力矩，aOz表示零升力气动坐标系的z 轴，aIz表示气流坐标系的z 轴。

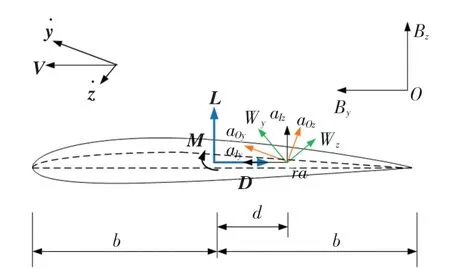
图3 机翼剖面图Fig.3 Profile of airfoil

根据亚音速不可压二维流的准定常空气动力学理论[15]，可得到机翼单元上气动系数的气动力和力矩，表示如下

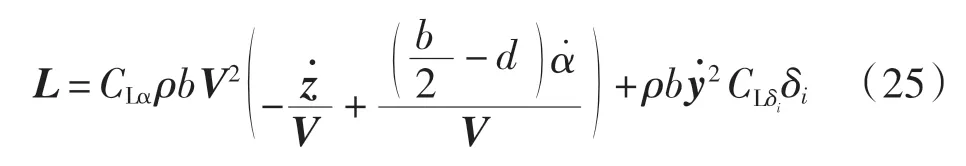
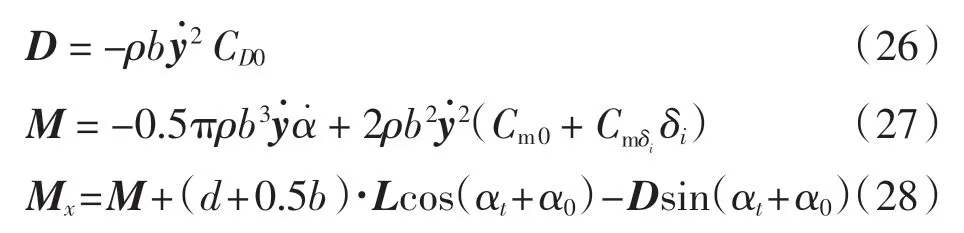
式中：M、Mx分别表示1/4 弦长处计算的力矩、1/2 弦长处计算的力矩，由于机翼弹性轴位于机翼1/2 弦长处， 而气动力和力矩是在1/4 弦长处的气动中心计算的，所以1/4 弦长处的力和力矩必须移到1/2 弦长处；ρ 是大气密度；α 是局部迎角；t 时刻的局部迎角αt=arctan是零升力迎角；CLα、CD0、Cm0是稳定性导数，分别表示升力线斜率、零升力矩系数和阻力系数；δi是飞机上舵面的偏转量（i=a、e、r 分别表示副翼、升降舵、方向舵）；CLδi、Cmδi是控制导数。 需要注意的是，稳定性导数和控制导数表示的含义与飞行动力学中表示的含义不同。 例如，在飞行动力学中，稳定性导数CLα表示迎角变化对飞机升力的影响，控制导数Cmδe表示升降舵偏转对飞机重心位置附近俯仰力矩的影响；在此处，稳定性导数CLα表示迎角变化对翼型截面所在当地机翼单元升力的影响，控制导数Cmδe表示升降舵偏转对翼型截面1/4 弦长处翼型截面当地所在机翼单元俯仰力矩的影响。

气动力系数通过Tornado 代码计算，该代码是Tomas Melin 采用涡格法开发的亚声速机翼气动特性分析程序。在Silva 的模型中，气动力系数是飞机上产生的力和力矩的总系数。在采用基于应变的非线性梁模型建立的刚弹耦合模型中，气动力系数是沿机翼展长分布的。 要调整沿机翼展长方向上气动力系数的分布，气动力系数的分布结果必须与用刚体方法建模产生的力和力矩效果相同。以飞机升力系数CLα为例，计算公式为

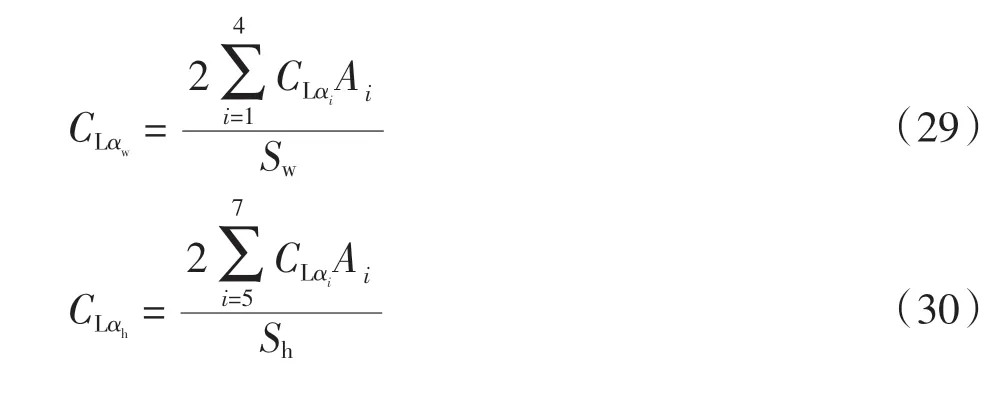
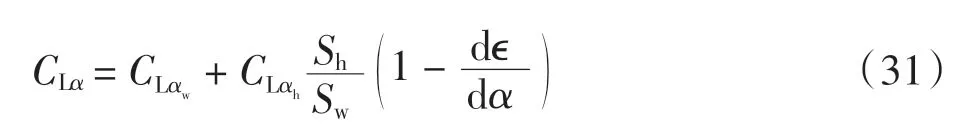
式中：CLαw、CLαh分别表示机翼升力线斜率和平尾升力线斜率，Sw、Sh分别表示机翼面积和平尾面积；CLαi表示机翼第i 个单元的升力线斜率；Ai表示第i 个单元的面积；∊表示下洗。表2～表5 给出了飞机在速度为224.6 m/s、高度为10 000 m 平飞条件下等效的稳定性导数和控制导数分布值（其中CLαv表示垂尾升力线斜率）。

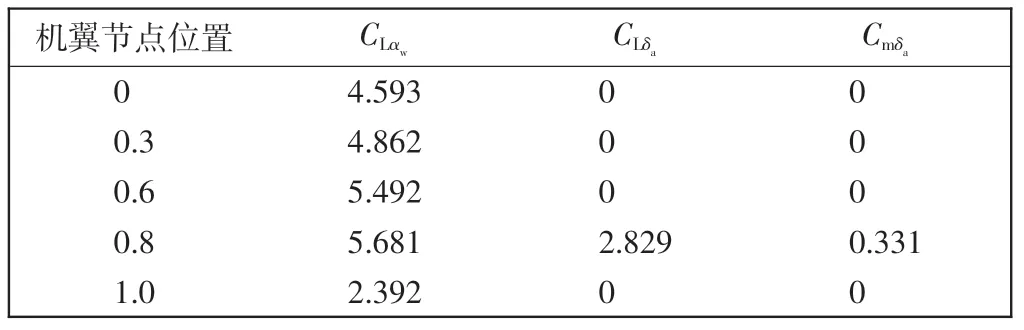
表2 机翼等效导数分布Tab.2 Equivalent derivative distribution of wing

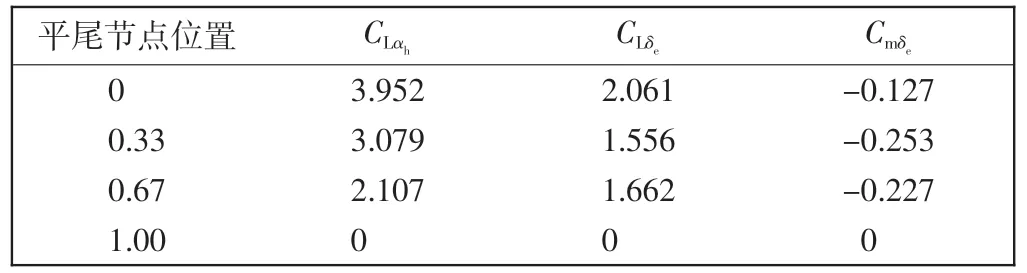
表3 平尾等效导数分布Tab.3 Equivalent derivatives distribution of horizontal tail

表4 垂尾等效导数分布Tab.4 Equivalent derivative distribution of vertical tail

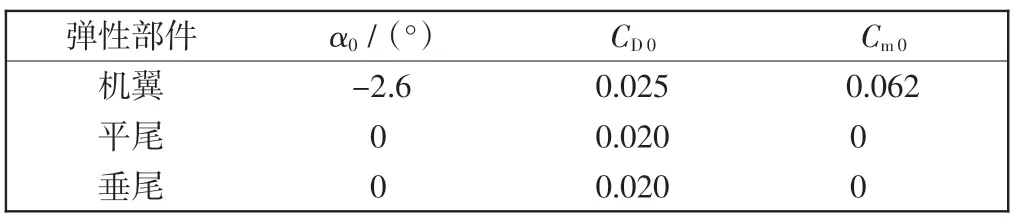
表5 弹性部件其他气动参数Tab.5 Aerodynamic parameters of other elastic components

3 仿真结果分析

3.1 滚转机动

在1 s 时给定-5°～5°周期为2 s 的副翼偏转输入，如图4（a）所示，滚转角速度随时间变化的曲线如图4（b）所示。 由图4 可看出，副翼偏转为正时，滚转角速度为负值。这是因为此时右侧机翼产生升力增加，左侧机翼产生升力减小，飞机向左侧滚转。通过刚弹耦合和刚体两种模型下滚转角速度的峰值差，计算出副翼偏转时刚弹耦合模型副翼效率比刚体模型低18.77%。

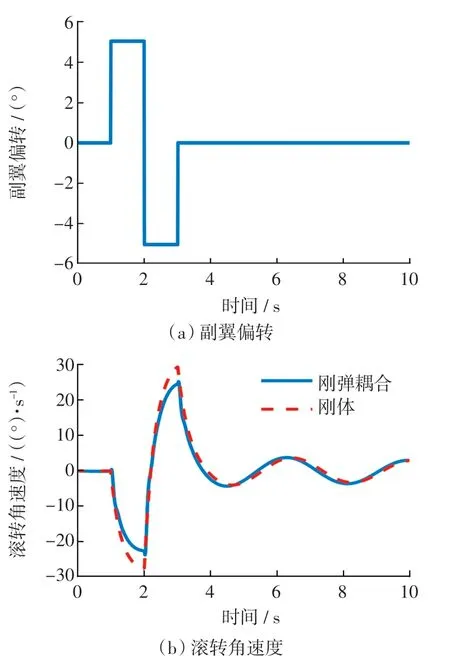
图4 副翼偏转响应Fig.4 Eeflection response of aileron

图5 给出了两侧机翼的翼根弯矩、 翼根扭矩、机翼挠度随时间的变化。 由图5 可看出，翼根弯矩比翼根扭矩大1 个数量级，对飞机滚转操纵影响最大的是机翼的弯曲。 副翼偏转时，由于刚弹耦合模型中机翼具有柔性，副翼偏转诱导两侧机翼扭转减小了当地等效迎角，另一方面两侧不对称的弯曲改变了气动载荷分布，从而造成飞机的滚转力矩减小，降低了副翼舵效率。

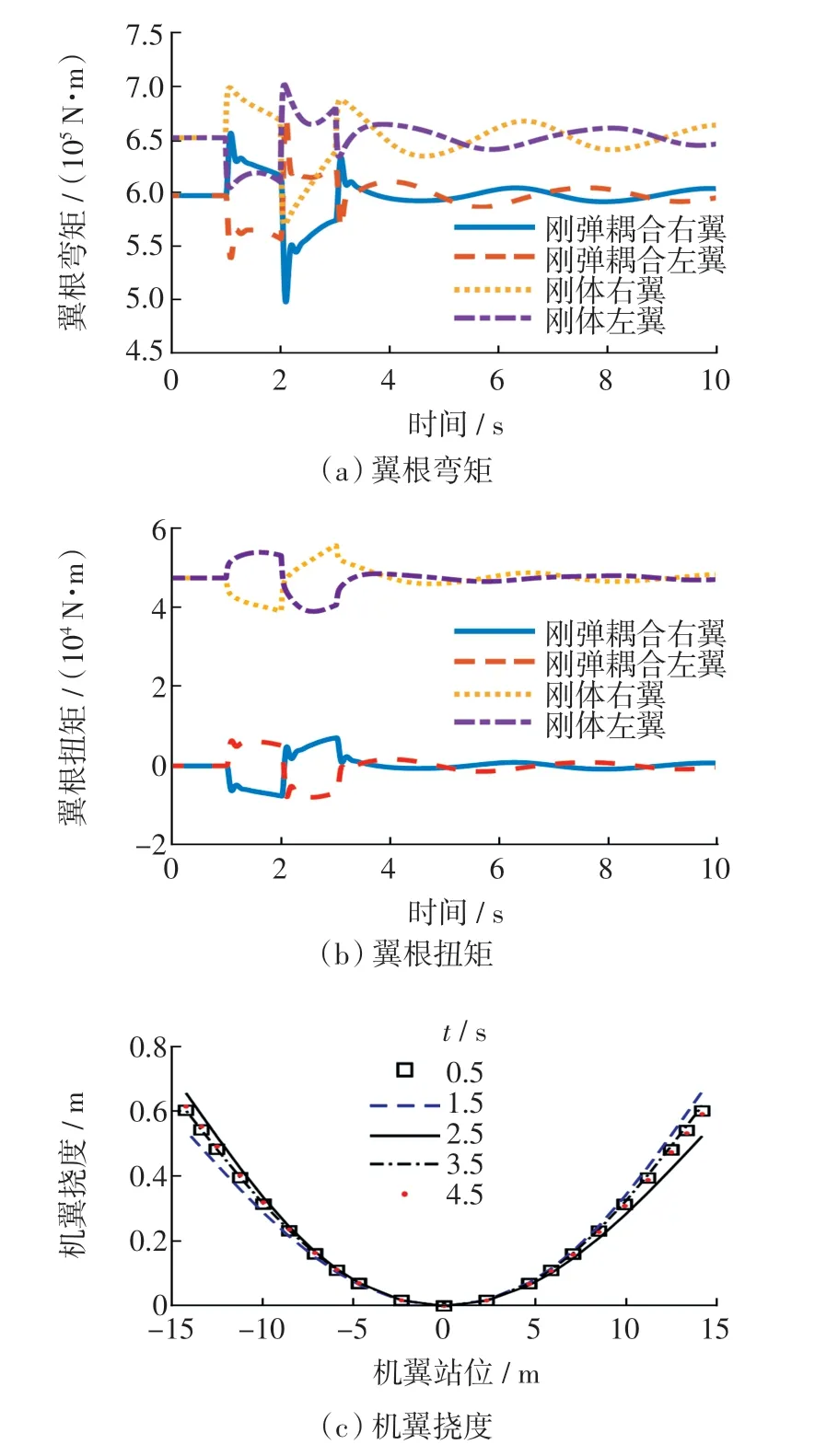
图5 机翼弹性响应（飞机滚转）Fig.5 Elastic response of wing（Aircraft roll）

3.2 垂直阵风响应

根据CCAR 25.341 条款中规定的离散突风设计准则得到

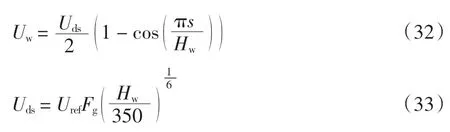
式中：Uw为阵风形状；Uds为设计阵风速度；s 为飞机进入阵风区的距离；Hw为阵风梯度，即达到其峰值速度时与飞机飞行航迹的平行距离，范围为9.1～106.7 m；Uref为参考阵风速度；Fg为飞行剖面缓和系数。 由于所选的飞机是在10 000 m 高度上建模，而10 000 m 高度被认为是飞机的运行高度。基于这一事实，参数Fg估计为1.0，计算得到Uds=10.61 m/s 的“1-cos”垂直离散阵风。图6 给出了俯仰角、俯仰角速度随时间变化的曲线。

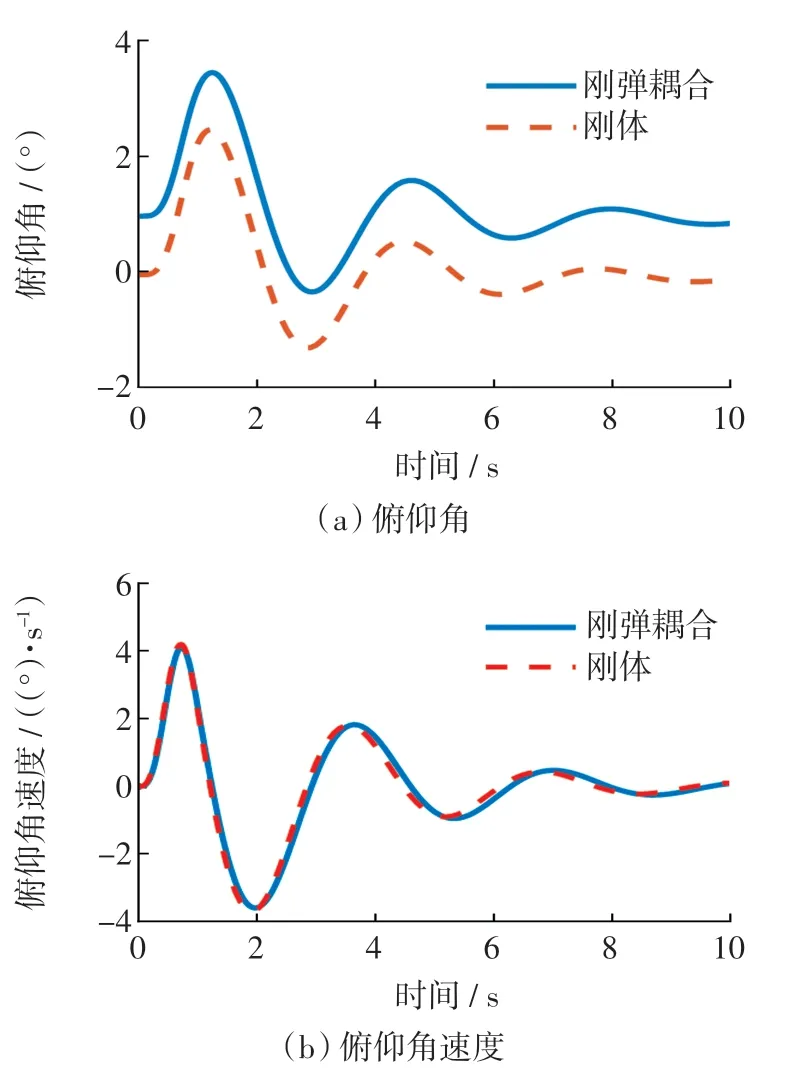
图6 垂直离散阵风响应Fig.6 Vertical discrete gust response

由图6 可看出，在受到垂直阵风扰动时刚弹耦合模型和刚体模型纵向响应基本一致，表明机翼的刚度对飞机纵向影响很小。

图7 给出了右翼根弯矩、右翼根扭矩、左右两侧机翼的挠度随时间的变化。

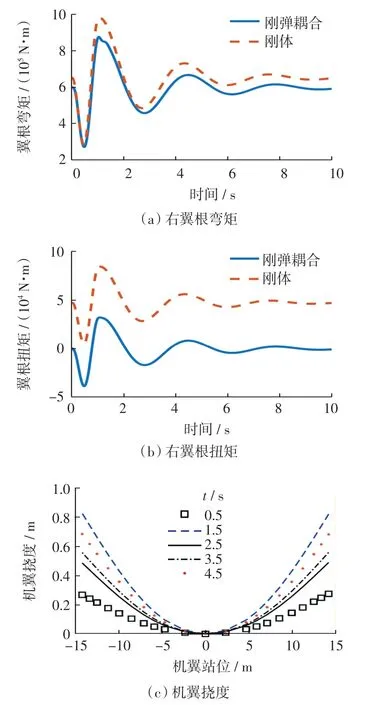
图7 机翼弹性响应（垂直阵风）Fig.7 Elastic response of wing(Vertical gust)

由图7 可看出，翼根弯矩比翼根扭矩大1 个数量级，垂直阵风对飞机影响最大的是机翼的弯曲。遭遇垂直阵风时，刚弹耦合模型预测的翼根弯矩峰值比刚体模型低8.35%。从能量角度考虑，阵风扰动的能量除了转化为刚体俯仰沉浮的动能外，还转化为机翼和尾翼的弹性能。因而，按照传统刚体假设预测的阵风载荷会过于保守，不利于飞机的减重。

4 结语

采用基于应变的非线性梁模型对柔性飞机建立了刚弹耦合的飞行动力学模型，通过时域仿真分析刚弹耦合模型和刚体模型的响应，得到了如下结论：①基于应变的刚弹耦合建模方法能够同时表达飞机弹性元件的变形和飞机的刚体运动，并模拟弹性变形与飞行动力学参数的相互影响；②在滚转机动仿真中，刚弹耦合模型的飞机能够模拟副翼舵效率的降低；③在垂直阵风响应仿真中，刚弹耦合模型与传统刚体建模相比具有更低的翼根弯矩。 基于应变的柔性飞机刚弹耦合建模方法可用于大柔性飞机的飞行控制律和阵风载荷减缓设计。