基于混合分布模型的海底管道腐蚀特性分析
2022-05-28李志黄小艳熊春宝聂东清
李志,黄小艳,熊春宝,聂东清
基于混合分布模型的海底管道腐蚀特性分析
李志1,2,黄小艳1,3,熊春宝4,聂东清5
(1.国家大坝安全工程技术研究中心,武汉 430010;2.长江科学院,武汉 430010;3.长江勘测规划设计研究有限责任公司,武汉 430010;4.天津大学 建筑工程学院,天津 300350;5.上海市政工程设计研究总院(集团)有限公司,上海 200092)
针对海底管道长期腐蚀损伤的随机性、多态性等问题,研究不同服役年限的海底管道腐蚀损伤分布特性及演化规律。提出了一种基于混合分布模型的海底管道腐蚀特性分析方法,该方法以老龄海底管道腐蚀损伤实测数据为基础,通过对不同服役年限下的海底管道腐蚀损伤特征进行统计分析,确定出海底管道腐蚀损伤的最佳分布模型,建立基于混合分布模型海底管道腐蚀损伤随机过程模型。进一步使用ARIMA方法对模型参数进行持续修正,并对管道腐蚀损伤进行预测。不同服役时间下的腐蚀损伤最佳分布不同,Weibull、Gumbel及Gamma分布模型均具有较好的拟合优度,且各分布模型随服役时间的增长呈现出不同的变化趋势,相应分布模型参数呈现出动态变化。结合ARIMA模型修正方法,充分利用实测数据能够不断降低模型的不确定性。海底管道的腐蚀损伤具有明显的多态性和随机性特征,很难采用单一分布模型对管道腐蚀损伤数据进行普遍性描述,既有的腐蚀损伤模型存在一定的不确定性及局限性,而基于混合分布模型的分析方法更能准确地反映海底管道长期腐蚀损伤的实际分布规律。
海底管道;腐蚀损伤特性;混合分布模型;Anderson-Darling检验;参数修正
海洋服役环境对海底管道具有强烈的腐蚀作用,是影响海底管道长期安全的主要问题之一[1-3]。据中国海洋石油总公司统计,1995—2012年该公司发生的海底管道故障中,腐蚀原因引起的占28.9%,且呈日益增长的趋势。2015年,胜利油田海底管道立管共发生5次管道腐蚀穿孔事故,其中主要以管道外保护层脱落导致的外壁严重腐蚀。
腐蚀安全评估是进行科学、合理的管道检测维护决策的重要依据[4-5],腐蚀模型作为管道腐蚀安全评估的重要前提,已成为管道安全评估研究的关键问题之一。为此,研究人员通过室内试验及现场调查对海工结构的腐蚀机理和发展过程进行了大量研究,并建立了多种腐蚀模型[6]。典型的确定型腐蚀模型主要有线性模型[7]、幂函数模型[8]、指数函数模型[9]。其中,线性模型将腐蚀速率假设为常量,主要适用于结构服役一定时间后的腐蚀稳定发展阶段;幂函数模型主要用于金属结构短期内局部腐蚀发展的描述;指数函数模型具有一定的灵活性,能较好地描述腐蚀多阶段的发展过程,但腐蚀模型参数取值难以确定。总体来看,该类模型对腐蚀过程进行了简化分析,因此模型形式简单、便于计算且能在一定程度上对结构的腐蚀过程进行描述,目前得到了广泛应用。为进一步考虑腐蚀过程的不确定性,提出了一些典型概率型腐蚀模型,如拓展线性模型[9]、拓展非线性模型[10]、广义极值模型[11]及基于贝叶斯更新的退化过程模型[12],该类模型通常假设腐蚀速率是服从正态分布或某一特定分布,严重忽略了腐蚀过程的复杂性与多态性。进一步地,许多学者提出一些典型的随机过程模型,如Markov模型[13]、布朗桥模型[14]、Gamma过程模型[15]、泊松过程模型[16]等。其中,Markov模型基于腐蚀数据得到概率转移矩阵,能够较好地描述埋地管道的点蚀情况;布朗桥模型主要适用于金属结构的蠕变损伤,其单调退化过程并不适合描述管道的腐蚀过程。尽管该类模型能够在一定程度上较好地描述出腐蚀过程的复杂性,但该类模型应用的基本假设前提是数据具有统计学同质性,随着服役时间的增加,管道工作条件、服役环境一旦发生变化,该类模型的适用性就不能得到很好地保证。基于贝叶斯网络模型[17-18]的腐蚀模型的建立需要对腐蚀机理进行详细调查分析。Shabarchin等[19]通过对管道内壁腐蚀因素进行综合分析,建立了贝叶斯网络模型对管内腐蚀速率进行预测分析。Kale等[20]考虑了多种腐蚀因素的影响,建立了多种管内腐蚀速率经验模型,该类模型形式较为复杂且模型参数较多,主要用于腐蚀管道的安全评估分析软件中,没有得到广泛推广。腐蚀损伤数据统计方面,极值统计法在最大腐蚀深度分布统计中得到了广泛的应用[21]。然而,有研究表明采用Gumbel分布进行腐蚀损伤的统计分析,其结果较为保守[22]。Melchers[23]在腐蚀损伤物理模型基础上,根据实测数据提出了全浸下低碳钢最大点蚀坑概率分布模型,并认为对较大坑深的点蚀,其最大蚀坑深度应服从正态分布,采用双概率密度模型来描述点蚀最大坑深分布更准确。Melchers[24]进一步研究了海水对低碳钢的腐蚀影响时发现,长期点蚀的最大腐蚀深度更符合Frechet分布。此外,Helio等[25]、Guo等[26]采用Weibull分布对管道结构的最大腐蚀深度进行统计分析。不论哪种模型,由于结构自身及服役环境条件的差异,这些模型及其参数往往存在较大的不确定性,且各模型的适用性具有较大的局限性,造成这种矛盾的主要原因在于人们对腐蚀损伤发展认识的局限性。因此,针对海底管道长期腐蚀问题,如何确定合适的腐蚀数据分布模型来降低模型选择的不确定性,以及如何降低模型参数估计的不确定性,是提高海底管道腐蚀失效预测及可靠度分析准确性的关键所在。此外,在管道安全管理过程中,有学者将这些腐蚀模型和可靠度评估结合,进行了管道的腐蚀失效预测、时变可靠度分析以及剩余寿命预测。过低的腐蚀损伤估计可能会导致管道发生泄漏或破裂事故,而过高的估计则可能导致不必要的维护。因此,选择合适的腐蚀模型对降低管道维护成本及提高海底管道安全性十分重要。
综上可知,许多金属结构腐蚀模型已应用于各类工程场景,但是如何选择合适的模型进行工程结构的腐蚀分析,仍存在较大的不确定性。例如海洋工程结构方面的腐蚀研究多集中于船舶结构,且结构腐蚀损伤评估过程中存在大量的不确定性。为此,本文提出了一种基于混合分布模型的海底管道腐蚀特性分析方法,该方法流程适用于多个管道服役场景。本文主要以胜利油田海底管道腐蚀损伤数据为实例,建立针对海底管道结构的腐蚀损伤模型,并对该方法进行了分析和验证。但在各场景中,基于实测数据建立完成的混合分布模型仅限于该场景下的应用,同时随着实测数据的不断累积,可实时加入分析模型进行模型的持续更新与修正,以降低模型参数估计的不确定性和提高模型的精度和鲁棒性。
1 方法流程
基于混合分布模型的海底管道腐蚀特性分析方法流程如图1所示,具体如下:
1)海底管道腐蚀损伤特征统计分析。收集整理海底管道腐蚀损伤实测数据,对海底管道腐蚀数据进行统计分析,筛选出海底管道腐蚀损伤的最佳分布模型。
2)混合分布模型建立。依据筛选出的腐蚀损伤分布模型,建立海底管道混合分布腐蚀损伤随机过程模型,降低腐蚀模型选择的不确定性;进一步结合ARIMA时序模型,对该腐蚀模型参数进行持续修正,降低模型参数的不确定性。
3)模型应用。利用该模型对海底管道腐蚀状态进行识别及预测。
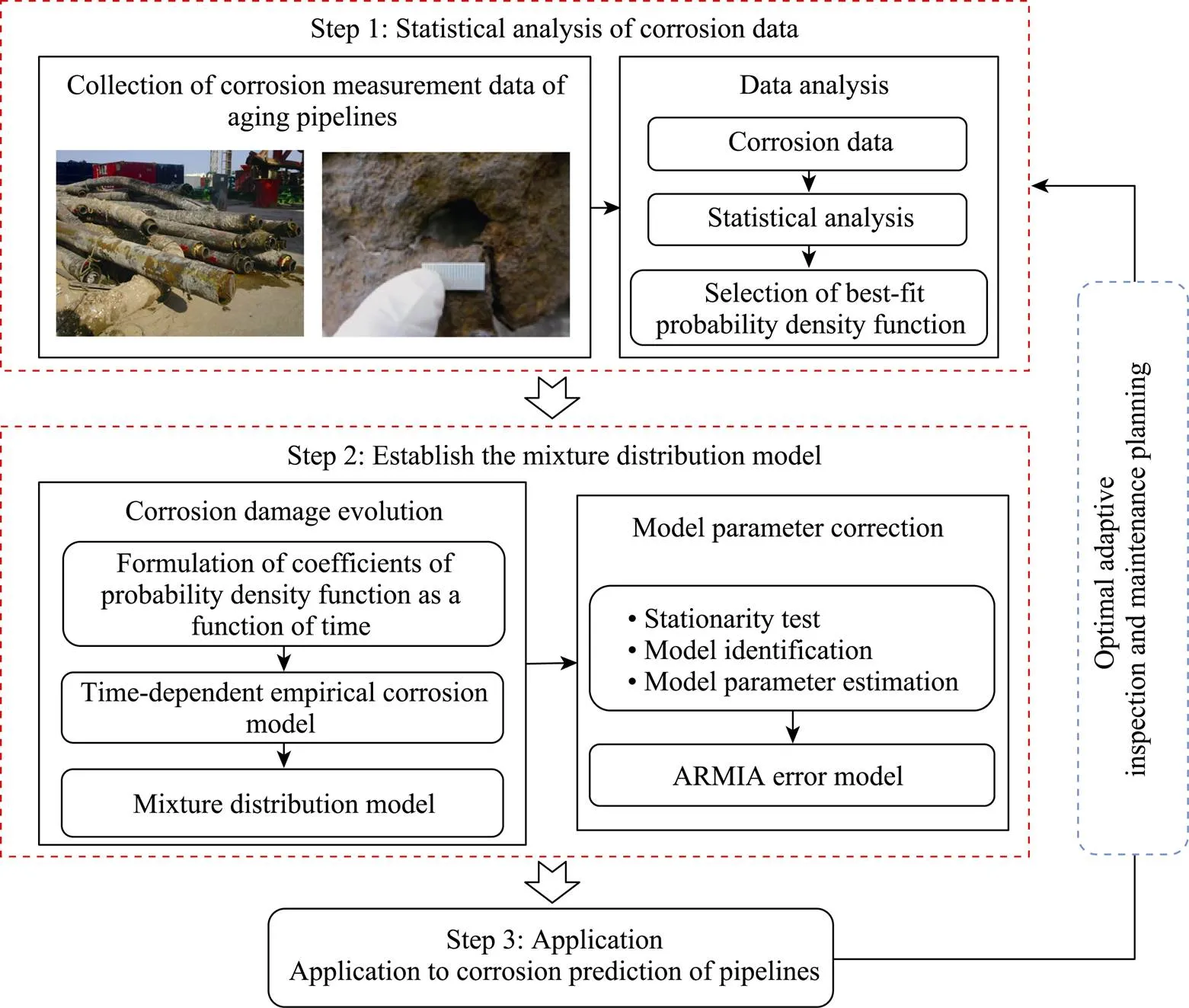
图1 混合分布腐蚀损伤模型及动态预测
2 海底管道腐蚀损伤特征统计分析
2.1 腐蚀损伤测量及统计
本次试验打捞回收胜利油田23条老龄管道的腐蚀失效段,包括16条输油管道、6条注水管道、1条试压管道,管道服役情况见图2。本文所选取的回收管道主要为同一海域内的老龄管道,其外部服役环境相同,通过对现场打捞管段内、外壁腐蚀情况进行观察可知:管道外壁存在大量的海生物附着,局部防腐层存在破损;管道内壁均存在垢层,去除垢层后观察到内表面以均匀腐蚀为主。对清除内壁和外壁腐蚀产物后管段的管壁进行壁厚测试,结果显示,管道减薄率为2%~16%,减薄严重部位主要分布于防腐涂层剥落的区域。在各管段外壁和内壁腐蚀严重的区域取样,使用扫描电镜对内壁取样位置处的腐蚀产物进行EDS观察,使用X射线衍射仪对内壁和外壁的腐蚀产物进行检测和分析,测试分析结果显示:输油管道和注水管道外壁腐蚀产物均以Fe的氧化物为主;注水管道内壁腐蚀产物以Fe的氧化物为主,输油管道内壁的腐蚀产物主要为FeCO3,这说明管道内外壁的腐蚀来源主要为潮湿环境导致的氧腐蚀。
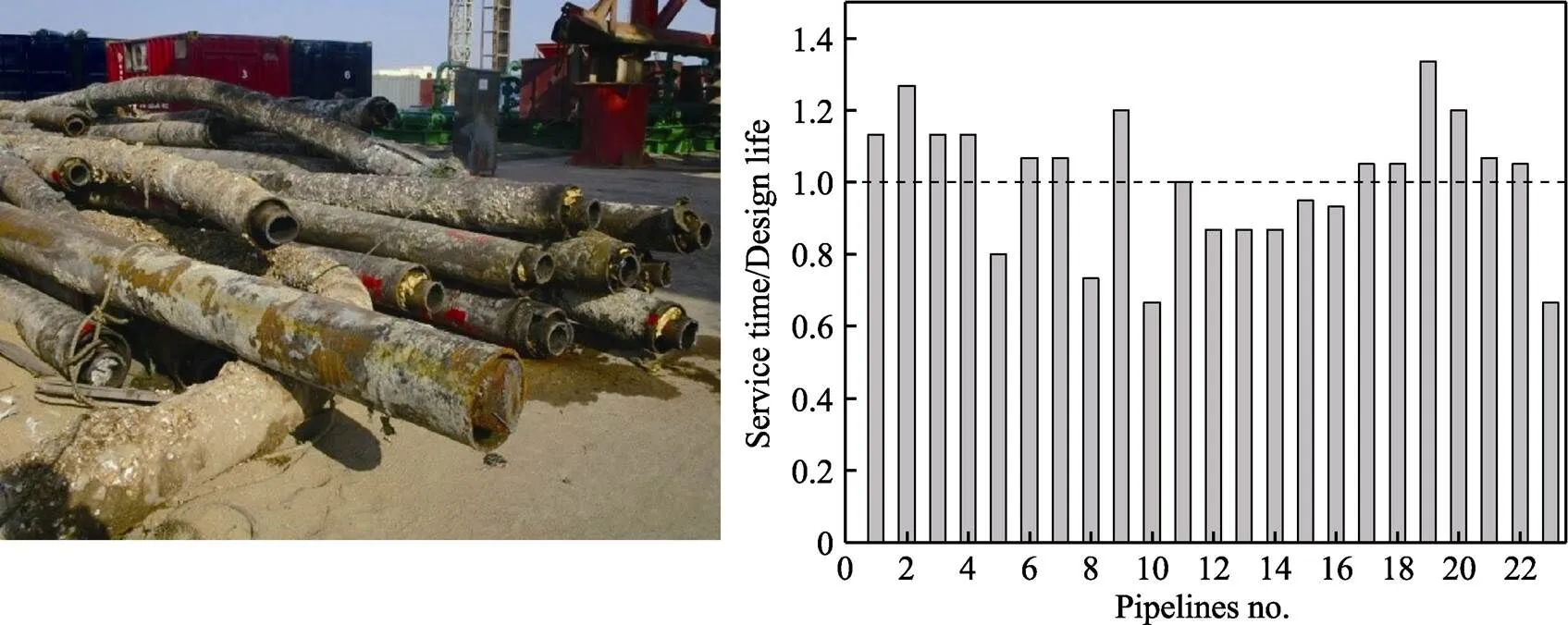
图2 被检测管道的服役情况
选取外壁腐蚀较为明显的管道截面并对其进行管壁厚度的取样检测,沿管体轴向每10 cm取一个测量截面,每个截面沿环向每90°(0°、90°、180°、270°)取测点进行壁厚测试(图3所示),采用超声波检测技术对剩余壁厚进行测量,获取管道外壁腐蚀损伤样本,共获取761个测点数据,管壁减薄测量结果见表
1。通过对腐蚀数据进行统计分析,得到不同年限对应的腐蚀损伤量的统计描述见图4、图5。统计结果显示:(1)尽管被检测管道试验取自同一地区,服役环境类似,但不同管道结构自身的差异及被测管道所采用的防腐措施不同,可能会引起管道的腐蚀程度不同,导致检测数据之间出现较大差异;(2)在获取服役10、11、19 a的管道腐蚀损伤数据过程中,被取样的管道中存在个别腐蚀较为严重的管道,其中有服役10 a的管道局部出现腐蚀穿孔破坏,这可能是该组数据离散程度较大的主要原因;(3)腐蚀损伤的标准差离散性较大,由峰度值和偏度值可知,其分布主要为非对称分布的偏态分布;(4)随着服役时间的延长,腐蚀损伤概率分布整体向坐标轴右侧移动,即管道腐蚀损伤量随着时间的延长而增加。

图3 管道壁腐蚀形貌及壁厚测点位置
表1 不同服役时间下海底管道腐蚀损伤量的统计结果

Tab.1 Statistics of corrosion damage of submarine pipeline wall at different service time
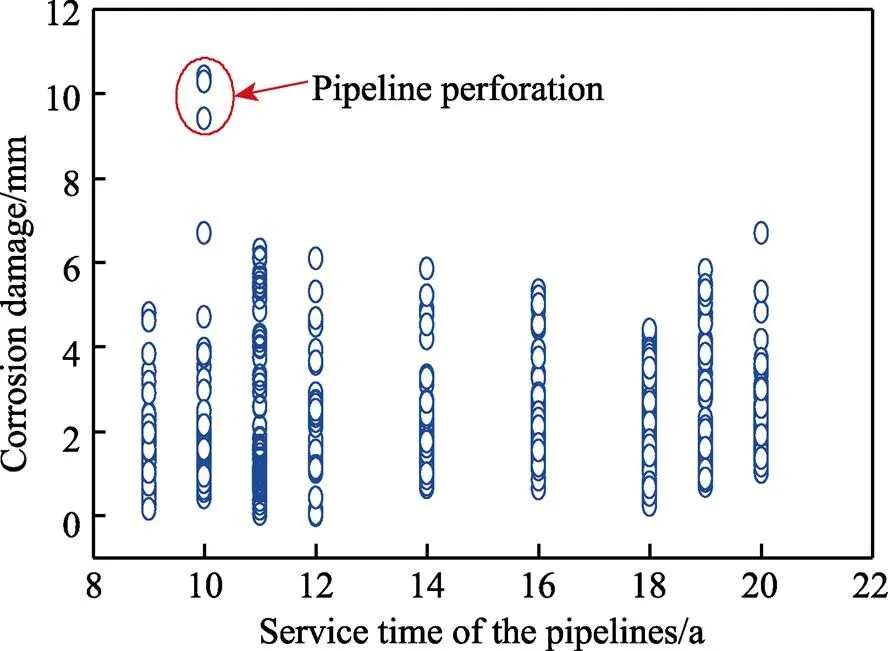
图4 腐蚀损伤散点分布
2.2 拟合优度检验
Anderson-Darling检验作为一种拟合优度检验量化解析算法,可用于样本数目较小(≥5)的情况,该检验通过计算样本分布函数(CDF)和经验分布函数(EDF)之间的二次Anderson-Darling距离来检定被检验数据符合某特定总体的程度,AD统计量值代表概率图中的点到拟合线的距离大小的加权平方和,统计量值越小,表示分布与数据拟合得越好。设腐蚀损伤数据样本(1,2, …,x)的CDF和EDF分别为(,)、F(),建立腐蚀样本顺序统计量(1)<(2)<…<(n),则样本数据的经验分布函数计算公式为:
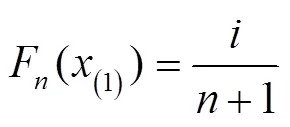
式中:为腐蚀数据样本个数;为个腐蚀数据从小到大排序的序号。二次Anderson-Darling距离统计量的表达式见式(2),其离散形式的表达式见式(3)。其中,为分布模型参数向量,Z为概率积分变换函数,Z=((i))。
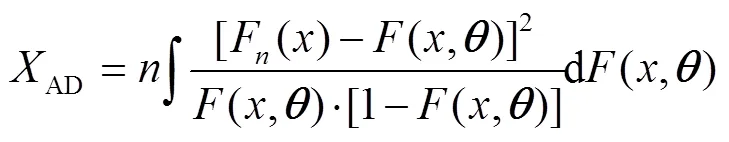
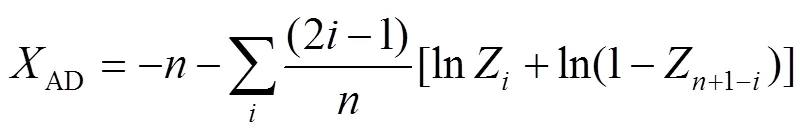
2.3 分布模型拟合效果分析
选择合适的统计模型是进行腐蚀损伤统计推断的关键。由于海底管道结构腐蚀损伤数据具有较大的离散性,导致能够描述该数据的分布有多个,通常人们根据试验数据来确定经验分布模型。然而,针对具体的海底管道结构,究竟该选哪一种分布模型,还需要对数据的不确定性进行分析。本文选用的备选模型有正态分布、对数正太分布、Weibull分布、3参数Weibull分布、Gamma分布、Gumbel分布、指数分布、2参数指数分布[4,13,27]。采用极大似然估计法对分布模型进行参数估计,AD检验结果见表2,分析结果可知:(1)不同服役时期的腐蚀损伤的最佳统计分布也不同,即随着服役时间的延长,腐蚀损伤并不服从同一分布,模型随着服役时间的增加也存在较大的不确定性,这也充分说明了海底管道腐蚀损伤发展具有较强的时变性及随机性,很难用统一的经验模型进行准确的描述;(2)由平均AD统计量结果可知,腐蚀损伤的最佳分布模型依次为3-Weibull分布>Weibull分布> Gumbel分布>Gamma分布>正态分布>对数正态分布>指数分布,其中Weibull分布和Gumbel分布的拟合结果较为接近,正态分布、对数正太分布以及指数分布拟合结果较差。
从整个服役期管道腐蚀损伤的角度看,对服役时间为9~20 a的腐蚀损伤数据的分布模型进行拟合优度检验,结果见表3,可知管道腐蚀损伤最佳分布模型依次为Gumbel分布>Weibull分布>3-Weibull分布> Gamma分布>正态分布>对数正态分布>指数分布。其中,正态分布、对数正态分布以及指数分布的拟合效果依然较差。考虑到:(1)在检测过程中发现,由于腐蚀涂层的保护作用,管道存在无腐蚀情况,即最小腐蚀损伤为0;(2)管道腐蚀存在多态性特征,仅仅采用某一分布模型对管道腐蚀损伤数据进行描述缺乏一定的普遍性。结合拟合优度检测结果,选取腐蚀损伤的Weibull分布、Gumbel分布及Gamma分布模型做进一步讨论,模型参数估计见表4和表5。
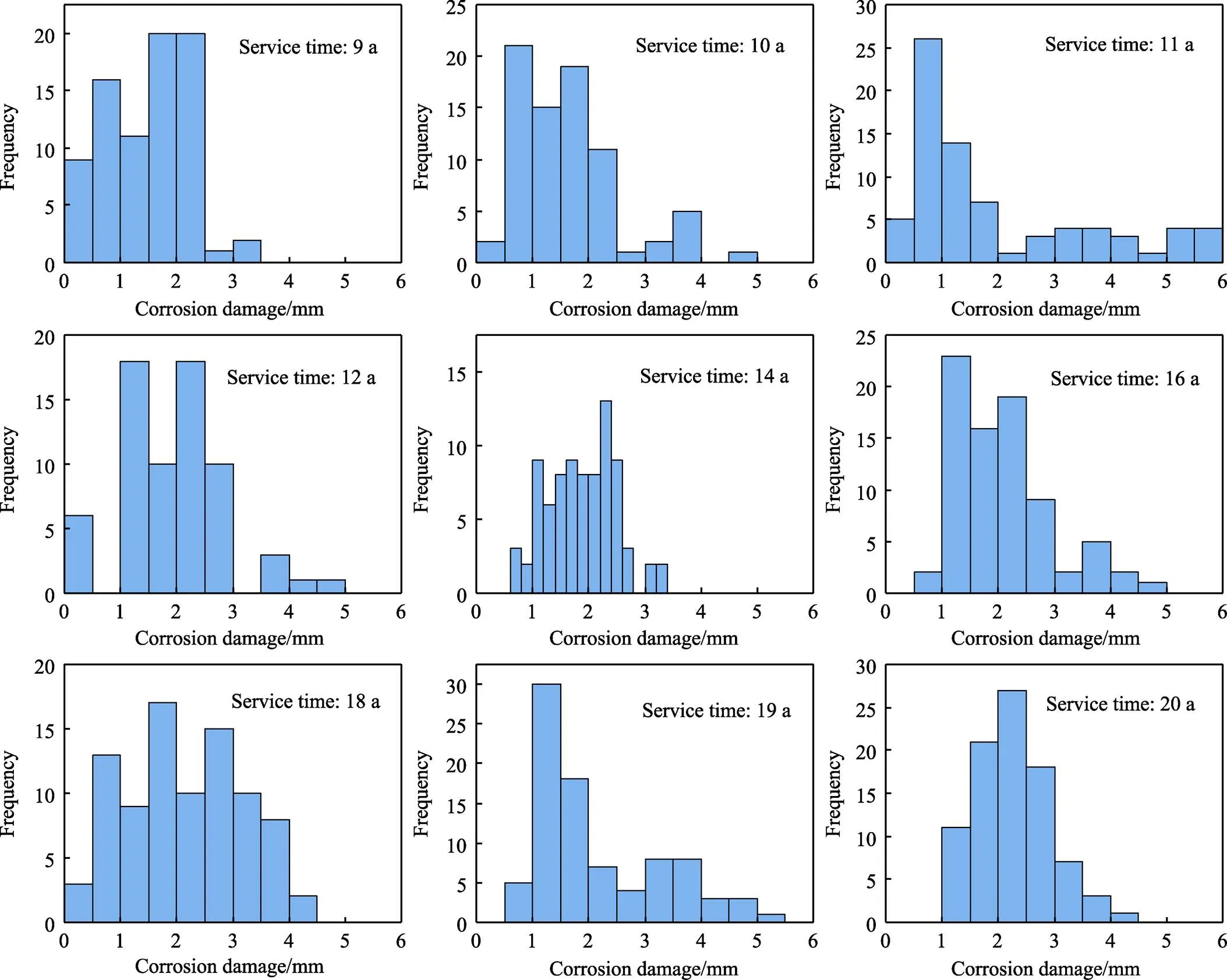
图5 不同服役时间下海底管道管壁腐蚀损伤量的统计结果
表2 腐蚀损伤数据的AD拟合优度检验结果
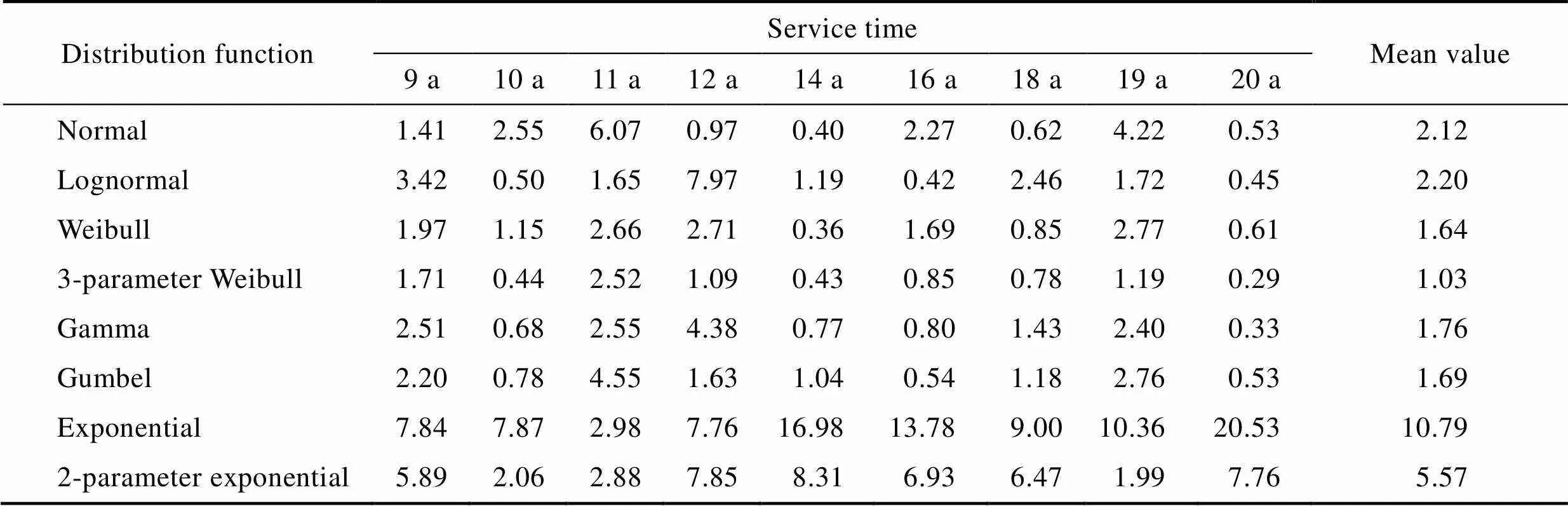
Tab.2 The Anderson-Darling test results of measuring goodness of corrosion damage data
表3 总体腐蚀损伤数据的AD拟合优度检验结果

Tab.3 The Anderson-Darling test results of measuring goodness of total corrosion damage data
表4 腐蚀损伤分布模型的参数估计值

Tab.4 Parameter estimation of distribution model of corrosion damage
表5 总体数据分布模型的参数估计值

Tab.5 Parameter estimation of distribution model of total corrosion damage data
3 混合分布模型建立
上述腐蚀损伤实测数据的分布拟合分析表明,Weibull分布、Gumbel分布以及Gamma分布均能较好地描述管道的腐蚀损伤发展情况。然而,这并不利于选择合适的腐蚀损伤模型,增加了模型建立过程的不确定性。此外,由于腐蚀损伤数据的随机性,使参数回归模型与实测数据之间存在一定误差,分析引起这种不确定性的来源主要有:(1)管道腐蚀机理的不确定性;(2)管道腐蚀环境的不确定性;(3)管道腐蚀多态性发展的不确定性;(4)管道服役状态的不确定性;(5)获取海底管道腐蚀损伤数据较难,导致样本数据不足。
这些不确定性导致的结果主要体现在:(1)腐蚀损伤模型的选择问题,由于海底管道腐蚀损伤较强的随机特性,若采用单一的数学模型很难对管道腐蚀损伤的发展进行准确描述,若强行拟合又将使得模型函数形式过于繁杂,且模型精度也不能得到保证;(2)这些不确定性还体现在各模型参数中,而模型参数的确定对管道安全可靠性评估以及检测维护决策都有重要影响。为合理解决模型选择问题及参数估计问题,本文通过加权融合法综合考虑3种分布模型同时存在的情况,建立混合分布腐蚀损伤模型,其表达为:
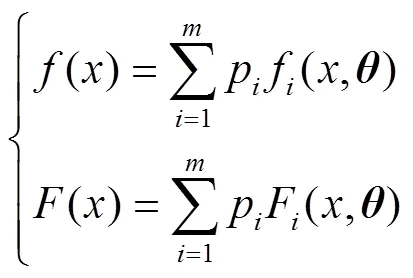
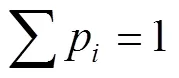
4 模型验证及应用
4.1 模型精度验证
由实测结果分析可知,在假定腐蚀损伤同分布的情况下,其分布情况随服役时间的延长依然呈现出不同的变化趋势,相应的分布模型参数随腐蚀时间的增加呈现出动态变化,因此腐蚀损伤发展可看作是服从一定分布的非平稳随机过程。本文根据模型参数估计结果,建立参数变量的回归模型,通过参数变量的动态变化对腐蚀损伤的随机动态演化过程进行分析,模型表达式见式(5),式中,a为回归系数,为多项式阶数,为观测时间。
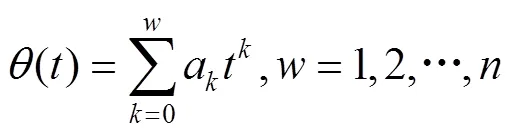
Weibull分布、Gumbel分布以及Gamma分布模型参数拟合结果见表6和图6。根据AD统计量结果,模型权重见表7和图7。由图7可知,各分布模型权重没有明显的规律性,不确定性较大,变化区间为0.15~0.55。图8为基于实测数据拟合的混合分布模型与基于参数回归的混合分布模型对比。
表6 Weibull、Gumbel、Gamma分布模型参数的拟合结果

Tab.6 Approximation of Weibull, Gumbel, Gamma distribution parameters

图6 各分布模型参数的拟合结果
表7 各分布模型的权重

Tab.7 The weight of each distributed model
均方根误差(RMSE)是统计学中常用的定量分析不同方法对同一样本拟合精度的检验指标,其表达式为:

式中:n为观测数据个数;yobs,i为实际观测数据序列;ypre,i为模型估计值序列。基于实测数据的分布模型和基于参数回归的分布模型分别与实测数据进行误差比较分析,分析结果见表8。由表8可知,混合分布模型结合了不同模型的优点,显著提高了拟合精度,这说明混合分布模型对海底管道腐蚀损伤发展描述的有效性。
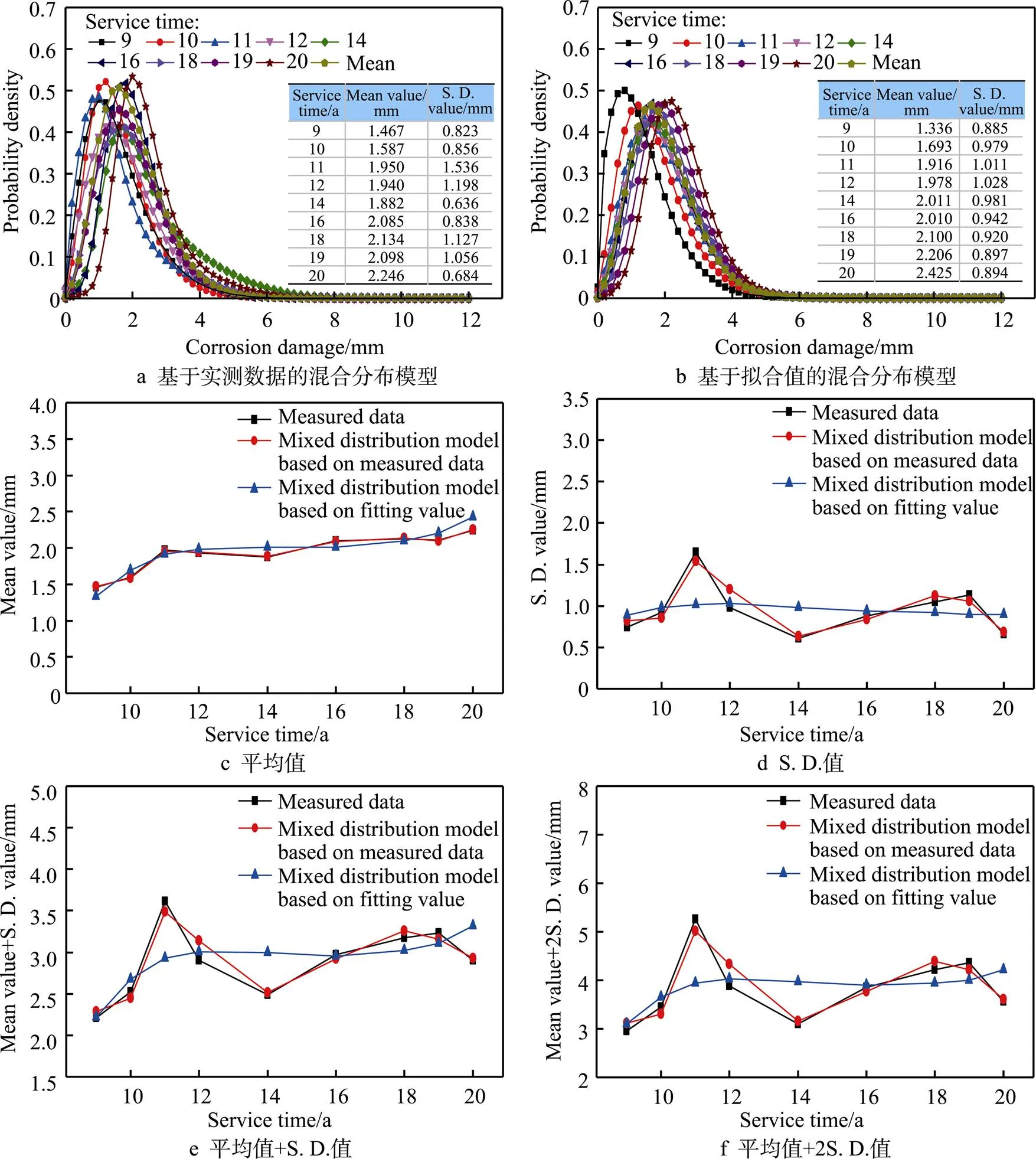
图8 混合分布腐蚀损伤模型对比分析
表8 实测数据拟合模型与参数回归模型的均方根误差

Tab.8 The ERMSE of mixed distribution model based on measured data and fitting values
4.2 误差修正
海底管道结构腐蚀损伤发展的非平稳随机过程特性是构建ARIMA模型的物理基础,基于ARIMA模型的海底腐蚀损伤预测基本思路是:在参数回归模型基础上,对模型参数误差建立ARIMA模型,继而对腐蚀损伤分布模型进行动态校正并预测,预测结果如图9所示。
由图9可以看出,前期数据预测误差相对较大,而后期数据的预测精度相对较高,因此在实际工程中,随着腐蚀损伤实测数据的持续及累积,模型预测精度会不断提高。模型参数修正结果如表9所示。经参数修正后,基于实测数据的分布模型和基于参数回归的分布模型分别与实测数据进行误差比较分析,分析结果见表10。结果显示,经过参数误差修正的各个分布模型的精度均得到了一定提高。
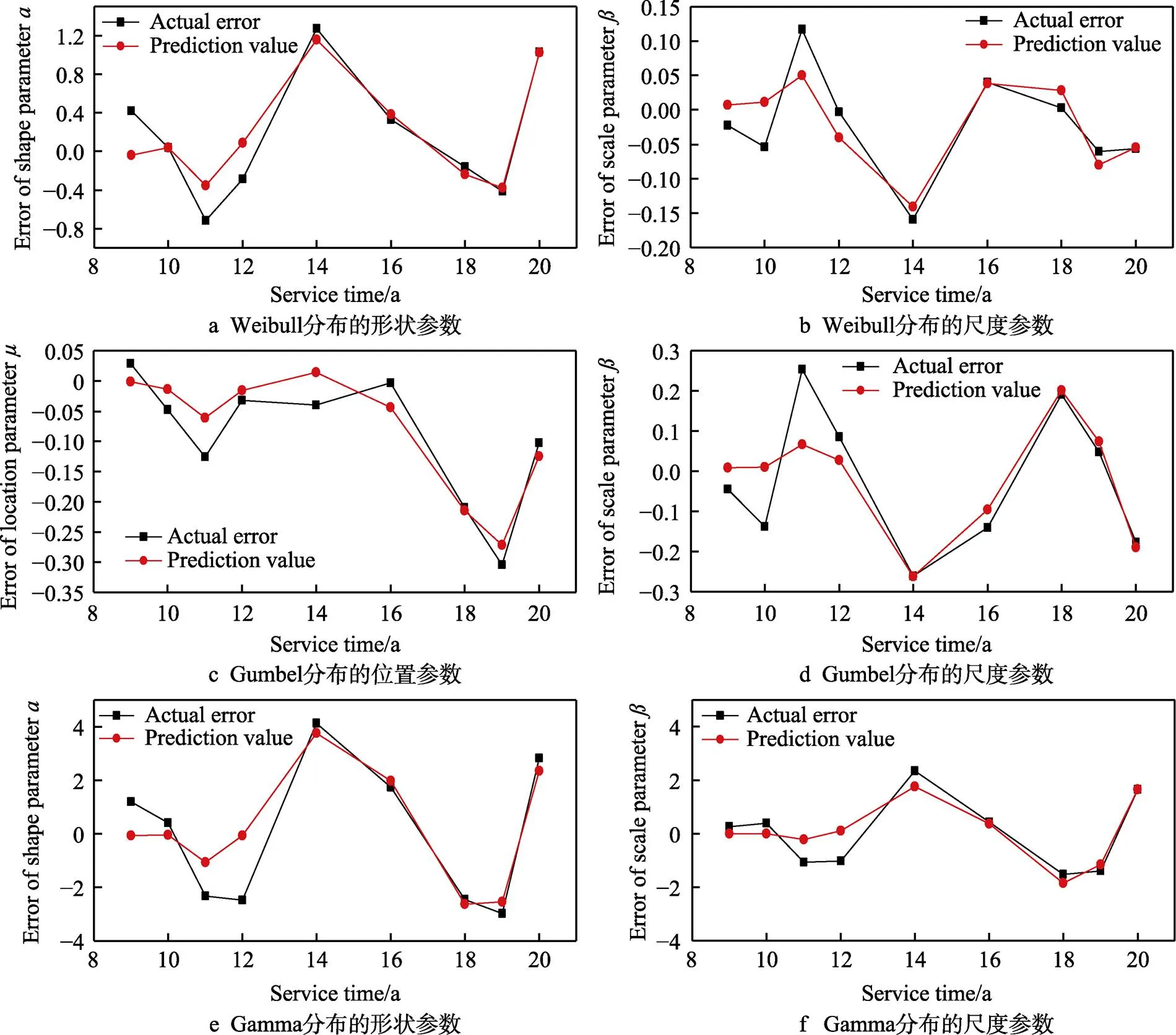
图9 各分布模型参数的误差预测
表9 各模型参数修正
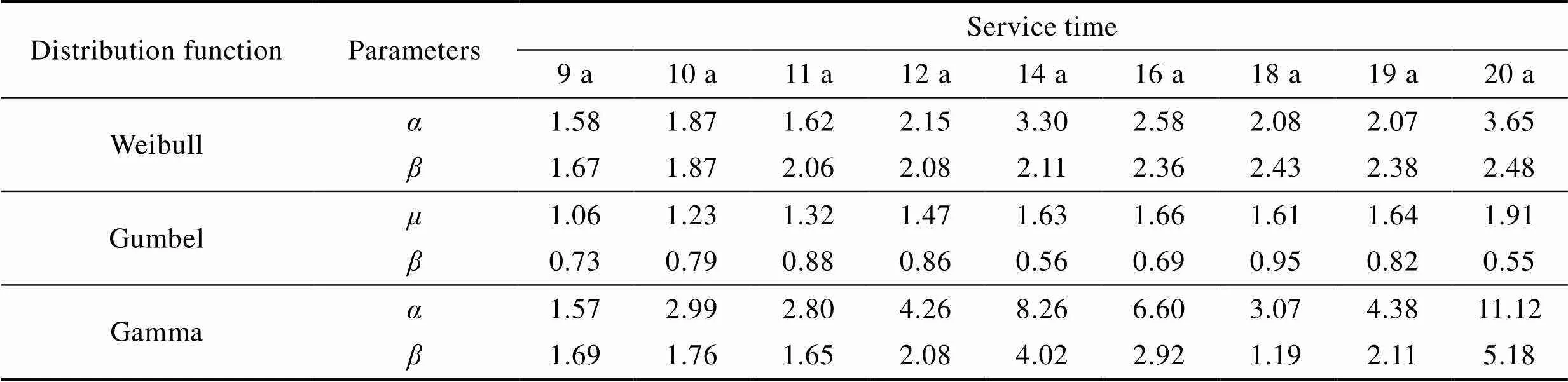
Tab.9 The modification of each model parameters
表10 各模型参数修正前后的均方根误差
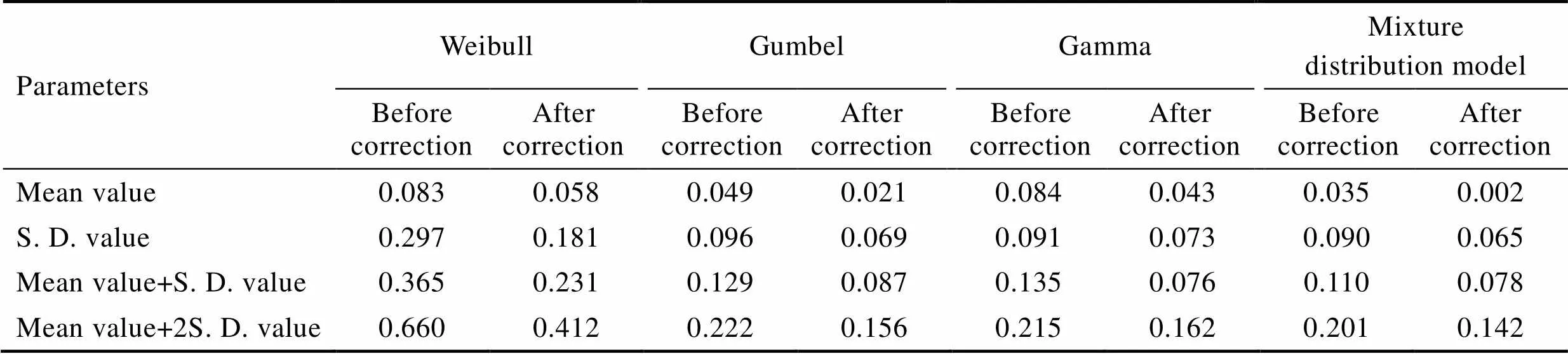
Tab.10 The ERMSE of each distribution model parameter after error correction
4.3 管道腐蚀动态预测
利用该模型预测未来一段时间管道的腐蚀损伤分布,分布模型参数预测结果见表11。结合混合分布腐蚀损伤模型,模型参数修正前后的腐蚀损伤预测结果见图10。由图10可知,腐蚀损伤随服役时间的延长呈明显的增长趋势;模型参数修正前,腐蚀损伤的增长呈现出较强的规律性,其分布呈现出较明显的渐变性,而经过模型参数修正,管道腐蚀损伤的增加和腐蚀损伤分布的渐变过程均呈现出一定的不确定性,这更符合实际腐蚀损伤的情况。
表11 各模型参数的预测值
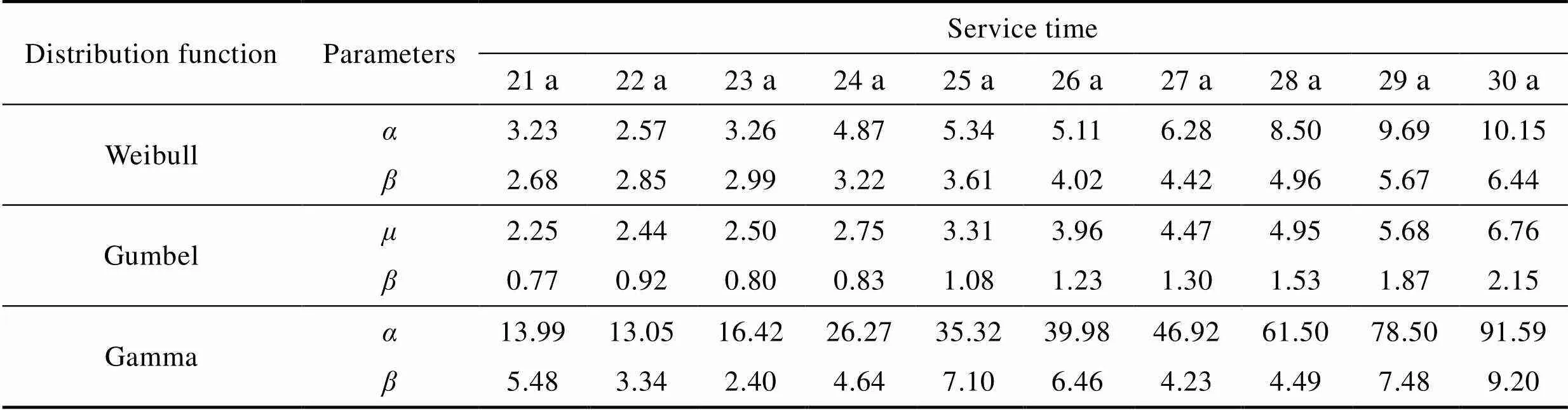
Tab.11 The predicted values of each model parameters
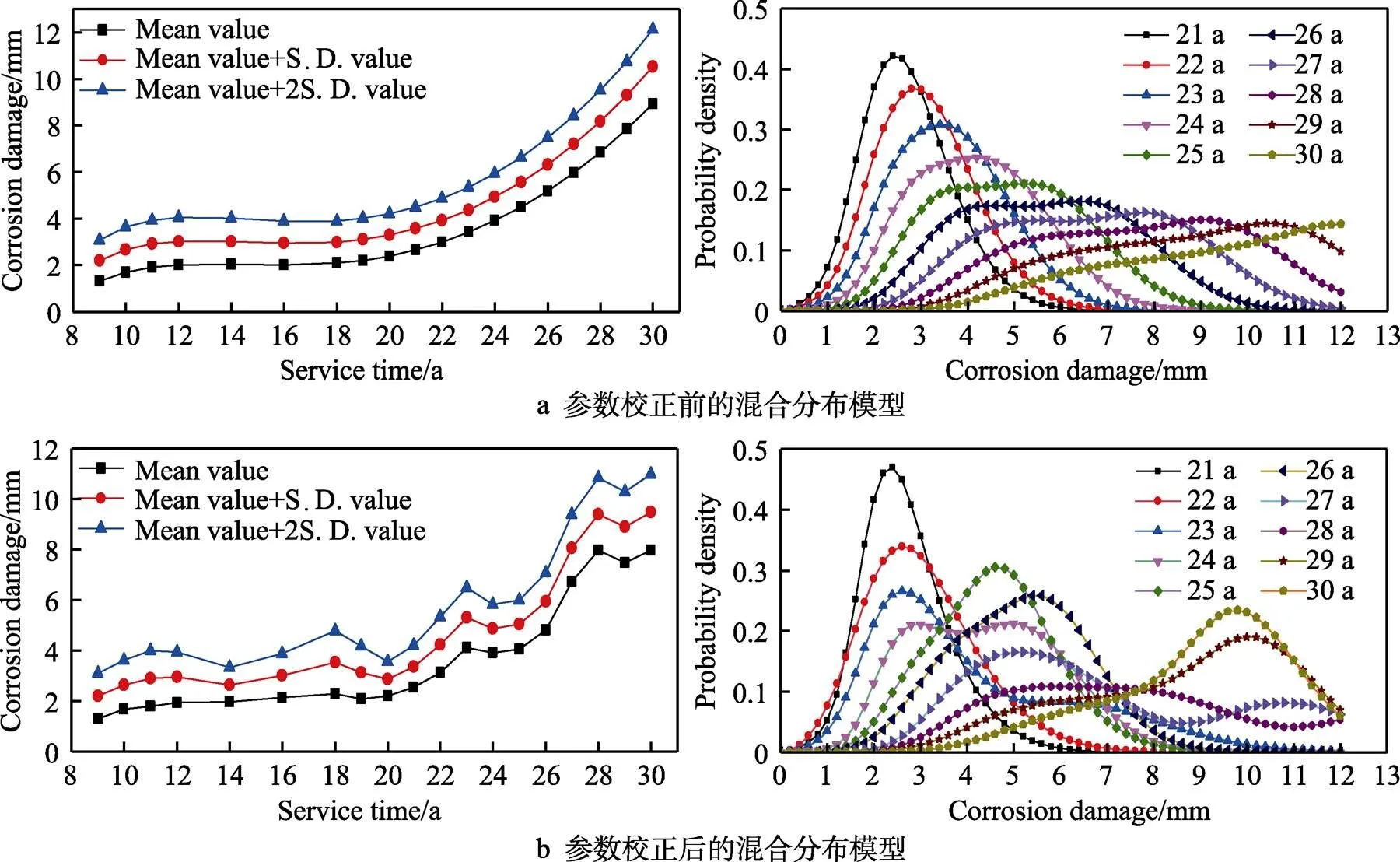
图10 混合分布腐蚀损伤预测
5 结论
1)不同服役时间下的腐蚀损伤最佳分布不同,Weibull、Gumbel及Gamma分布模型均具有较好的拟合优度,表明海底管道的腐蚀损伤具有明显的多态性特征,很难采用单一分布模型对管道腐蚀损伤数据进行普遍性描述,导致既有腐蚀损伤模型的应用存在一定的不确定性及局限性。
2)各分布模型随服役时间的延长呈现出不同的变化趋势,相应分布模型参数呈现出动态变化,表明海底管道的腐蚀损伤发展具有明显的随机时变特性。
3)通过模型参数回归拟合建立混合分布腐蚀损伤随机过程模型,并结合误差分析和ARIMA时序模型对模型进行持续修正,充分利用实测数据不断降低模型的不确定性,分析结果显示,随着腐蚀损伤实测数据的持续及累积,模型预测精度会不断提高。
[1] NETTO T A, FERRAZ U S, ESTEFEN S F. The Effect of Corrosion Defects on the Burst Pressure of Pipelines[J]. Journal of Constructional Steel Research, 2005, 61(8): 1185-1204.
[2] 秦鹏程, 熊春宝, 李志, 等. 考虑多腐蚀缺陷作用效应的海底管道失效压力分析[J]. 表面技术, 2020, 49(1): 237-244.
QIN Peng-cheng, XIONG Chun-bao, LI Zhi, et al. Failure Pressure Assessment of Submarine Pipelines Considering the Effects of Multiple Corrosion Defects Interaction[J]. Surface Technology, 2020, 49(1): 237-244.
[3] 骆正山, 秦越, 张新生, 等. 基于LASSO-WOA-LSSVM的海洋管线外腐蚀速率预测[J]. 表面技术, 2021, 50(5): 245-252.
LUO Zheng-shan, QIN Yue, ZHANG Xin-sheng, et al. Prediction of External Corrosion Rate of Marine Pipelines Based on LASSO-WOA-LSSVM[J]. Surface Technology, 2021, 50(5): 245-252.
[4] KHAN F, HOWARD R. Statistical Approach to Inspection Planning and Integrity Assessment[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2007, 49(1): 26-36.
[5] 张新生, 张平. 不完全维修下海底腐蚀管道剩余寿命预测[J]. 系统工程理论与实践, 2019, 39(11): 2984- 2994.
ZHANG Xin-sheng, ZHANG Ping. Remaining Useful Life Prediction of Corroded Submarine Pipelines under Imperfect Maintenance[J]. Systems Engineering-Theory & Practice, 2019, 39(11): 2984-2994.
[6] VANAEI H R, ESLAMI A, EGBEWANDE A. A Review on Pipeline Corrosion, In-Line Inspection (ILI), and Corrosion Growth Rate Models[J]. International Journal of Pressure Vessels and Piping, 2017, 149: 43-54.
[7] JI Jian, ROBERT D J, ZHANG Chun-shun, et al. Probabilistic Physical Modelling of Corroded Cast Iron Pipes for Lifetime Prediction[J]. Structural Safety, 2017, 64: 62-75.
[8] PAIK J K, THAYAMBALLI A K, PARK Y I, et al. A Time-Dependent Corrosion Wastage Model for Seawater Ballast Tank Structures of Ships[J]. Corrosion Science, 2004, 46(2): 471-486.
[9] QIN Sheng-ping, CUI Wei-cheng. Effect of Corrosion Models on the Time-Dependent Reliability of Steel Plated Elements[J]. Marine Structures, 2003, 16(1): 15-34.
[10] SOARES C G, GARBATOV Y, ZAYED A, et al. Influence of Environmental Factors on Corrosion of Ship Structures in Marine Atmosphere[J]. Corrosion Science, 2009, 51(9): 2014-2026.
[11] MELCHERS R E. Extreme Value Statistics and Long- Term Marine Pitting Corrosion of Steel[J]. Probabilistic Engineering Mechanics, 2008, 23(4): 482-488.
[12] ZHANG Shen-wei, ZHOU Wen-xing. Bayesian Dynamic Linear Model for Growth of Corrosion Defects on Energy Pipelines[J]. Reliability Engineering & System Safety, 2014, 128: 24-31.
[13] OSSAI C I, BOSWELL B, DAVIES I J. Reliability Analysis and Performance Predictions of Aged Pipelines Subjected to Internal Corrosion: A Markov Modelling Technique[C]//Proceedings of ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, Massachusetts, USA. 2016
[14] WANG Hui, YAJIMA A, LIANG R Y, et al. Reliability- Based Temporal and Spatial Maintenance Strategy for Integrity Management of Corroded Underground Pipelines[J]. Structure and Infrastructure Engineering, 2016, 12(10): 1281-1294.
[15] MAHMOODIAN M, ALANI M A. A Gamma Distributed Degradation Rate Model for Reliability Analysis of Concrete Pipes Subject to Sulphide Corrosion[J]. International Journal of Reliability and Safety, 2014, 8(1): 19.
[16] PESINIS K, TEE K F. Statistical Model and Structural Reliability Analysis for Onshore Gas Transmission Pipelines[J]. Engineering Failure Analysis, 2017, 82: 1-15.
[17] BHANDARI J, KHAN F, ABBASSI R, et al. Pitting Degradation Modeling of Ocean Steel Structures Using Bayesian Network[J]. Journal of Offshore Mechanics and Arctic Engineering, 2017, 139(5): 051402.
[18] 骆正山, 赵乐新, 王小完. 基于动态贝叶斯网络的海底管道点蚀疲劳损伤失效模型研究[J].表面技术, 2020, 49(1): 269-275.
LUO Zheng-shan, ZHAO Le-xin, WANG Xiao-wan. Failure Model for Pitting Fatigue Damaged Pipeline of Subsea Based on Dynamic Bayesian Network[J]. Surface technology, 2020, 49(1): 269-275.
[19] SHABARCHIN O, TESFAMARIAM S. Internal Corrosion Hazard Assessment of Oil & Gas Pipelines Using Bayesian Belief Network Model[J]. Journal of Loss Prevention in the Process Industries, 2016, 40: 479-495.
[20] KALE A, THACKER B H, SRIDHAR N, et al. A Probabilistic Model for Internal Corrosion of Gas Pipelines[C]// Proceedings of 2004 International Pipeline Conference. Calgary: [s. n.], 2008: 2437-2445.
[21] CHAVES I A, MELCHERS R E. Extreme Value Analysis for Assessing Structural Reliability of Welded Offshore Steel Structures[J]. Structural Safety, 2014, 50: 9-15.
[22] 骆正山, 王瑞, 毕傲睿. Frechet分布的海底油气管道腐蚀预测[J]. 腐蚀与防护, 2017, 38(3): 214-218.
LUO Zheng-shan, WANG Rui, BI Ao-rui. Corrosion Forecast of Offshore Oil and Gas Pipelines Based on Frechet Distribution[J]. Corrosion & Protection, 2017, 38(3): 214-218.
[23] MELCHERS R E. Statistical Characterization of Pitting Corrosion-Part 1: Data Analysis[J]. Corrosion, 2005, 61(7): 655-664.
[24] MELCHERS R E. Estimating Uncertainty in Maximum Pit Depth from Limited Observational Data[J]. Corrosion Engineering, Science and Technology, 2010, 45(3): 240-248.
[25] DA CUNHA BISAGGIO H, NETTO T A. Predictive Analyses of the Integrity of Corroded Pipelines Based on Concepts of Structural Reliability and Bayesian Inference[J]. Marine Structures, 2015, 41: 180-199.
[26] GUO Jin-ting, WANG Ge, IVANOV L, et al. Time-Varying Ultimate Strength of Aging Tanker Deck Plate Considering Corrosion Effect[J]. Marine Structures, 2008, 21(4): 402-419.
[27] MOHD M H, KIM D K, KIM D W, et al. A Time-Variant Corrosion Wastage Model for Subsea Gas Pipelines[J]. Ships and Offshore Structures, 2014, 9(2): 161-176.
An Investigation into the Corrosion Behavior of Subsea Pipelines with the Mixture Distribution Model
1,2,1,3,4,5
(1. National Center for Dam Safety Engineering Technology Research, Wuhan 430010, China; 2. Changjiang River Scientific Research Institute, Wuhan 430010, China; 3. Changjiang Institute of Survey, Planning, Design and Research Co., Ltd., Wuhan 430010, China; 4. School of Civil Engineering, Tianjin University, Tianjin 300350, China; 5. Shanghai Municipal Engineering Design Institute (Group) Co., Ltd., Shanghai 200092, China)
Aiming at the randomness and polymorphism of long-term corrosion damage of submarine pipeline, the distribution characteristics and evolution law of corrosion damage of submarine pipeline with different service years are studied. An analysis method of corrosion characteristics of submarine pipeline based on mixture distribution model is proposed. Based on the measured data of corrosion damage of aging submarine pipeline, through the statistical analysis of corrosion damage characteristics of submarine pipeline under different service years, the optimal distribution model of corrosion damage of submarine pipeline is determined, and the random process model of corrosion damage of submarine pipeline based on mixture distribution model is established. Further, Arima method is established to continuously modify the model parameters and predict the pipeline corrosion damage. The results show that the optimal distribution of corrosion damage is different under different service time. Weibull, Gumbel and Gamma distribution models have good goodness of fit, and each distribution model shows different change trends with the increase of service time, and the corresponding distribution model parameters show dynamic changes; Combined with ARIMA model correction method, making full use of the measured data can continuously reduce the uncertainty of the model. The corrosion damage of submarine pipeline has obvious characteristics of polymorphism and randomness. It is difficult to use a single distribution model to generally describe the pipeline corrosion damage data. The application of the existing corrosion damage model has certain uncertainty and limitations. The analysis method based on the mixture distribution model can more accurately reflect the actual distribution law of long-term corrosion damage of submarine pipeline.
submarine pipeline; corrosion damage behavior; mixture distribution model; Anderson-Darling test; parameter correction
Tg172
A
1001-3660(2022)05-0186-12
10.16490/j.cnki.issn.1001-3660.2022.05.020
2021–08–08;
2021–11–23
2021-08-08;
2021-11-23
中央级公益性科研院所基本科研业务费资助项目(长江科学院CKSF2019562/GC)
Fundamental Research Funds for Central Public Welfare Research Institutes (Changjiang River Scientific Research Institute CKSF2019562/GC)
李志(1989—),男,博士,工程师,主要研究方向为结构健康监测与安全评估、海底管道检测与完整性管理等。
LI Zhi (1989-), Male, Doctor, Engineer, Research focus: structural health monitoring and safety assessment, submarine pipeline inspection and integrity management.
李志, 黄小艳, 熊春宝, 等. 基于混合分布模型的海底管道腐蚀特性分析[J]. 表面技术, 2022, 51(5): 186-197.
LI Zhi, HUANG Xiao-yan, XIONG Chun-bao, et al. An Investigation into the Corrosion Behavior of Subsea Pipelines with the Mixture Distribution Model[J]. Surface Technology, 2022, 51(5): 186-197.
责任编辑:万长清
