基于Stackelberg 模型的大国国际货币主导权博弈分析
2022-05-27张应华陈建付
张应华,洪 勇,陈建付
(九江学院,江西 九江 332005)
一、引言
在国际社会体系中,谁掌握了国际货币发行与流通的主导权,谁就成为国际金融治理体系的执牛耳者,谁就占据了国际金融的制高点。自现代世界经济发展以来,国际货币主导权一直由西方霸权国家所掌握。纵观历史,只要国际上出现霸权国家,它的国家货币就是国际主导货币,无论是以前大英帝国治下的英镑还是当今超级大国美国治下的美元概莫例外(蒙代尔,2003)[1]。国际货币主导权历来是大国之间竞争与博弈的焦点,尤其是在大国兴衰与更替之际尤为激烈,国际货币主导权的转移也成为国际秩序变迁的重要标志。
当今世界面临百年变局,大国博弈十分激烈,国际格局显著变化。中国日益走进世界舞台中央,成为与超级霸主美国之间博弈的主角,也是首个经济总量达到美国70%以上的国家。中美博弈事关中华民族伟大复兴和美国霸权地位的维护,还涉及世界力量体系的重构(倪峰,2020)[2],中美关系已经进入到国际秩序变革的主导权之争(朱峰,2020)[3]。自美国将中国视为首要战略竞争对手以来,中美博弈的烈度与深度正在加剧。
美元体系作为美国金融霸权的核心支柱,是货币金融时代讨论中美关系或大国博弈的重要背景(李晓,2022)[4]。以人民币与美元的国际竞争为核心的中美国际货币主导权博弈,将是中美两国全面博弈在经济领域的集中体现(张应华,2017)[5]。未来国际货币博弈主要集中在美元、欧元和人民币之间;主要国际货币国家在基于货币国际化的博弈中存在着囚徒困境(王婷婷,2014)[6],后发的国际货币与在位的国际货币之间也存在着博弈困境问题(代高琪,2021)[7]。
那么,中美争夺国际货币主导权博弈是否会陷入囚徒困境?中国如何破解中美国际货币主导权博弈的囚徒困境变被动为主动?基于这些思考,文章在借鉴以往学者们研究成果的基础上,通过构建大国国际货币主导权博弈的Stackelberg 博弈模型,集中研究守成大国与崛起大国之间基于国际货币主导权的博弈困境问题。
二、大国国际货币主导权博弈的Stackelberg 博弈模型及单次博弈均衡
1. 博弈问题描述与基本假设
守成大国与崛起大国之间基于国际货币主导权的博弈问题,本质上是大国间以争夺国际货币市场份额构建以本币为核心的国际货币体系等一系列博弈过程。文章在Fourcans&Warin(2001)的博弈分析框架基础之上,结合王婷婷(2014)和代高琪(2021)等从博弈参与方福利函数最大化考察博弈行为的思路,构建守成大国和崛起大国基于国际货币主导权竞争的Stackelberg博弈模型,其博弈关系如图1 所示。

图1 守成大国与崛起大国间的博弈关系
假设该博弈模型满足以下条件:
假设H1:博弈主体为守成大国A 和崛起大国B,只有这两个国家供给国际货币,并且他们的国际货币供给量分别为qA和qB,同期的国际货币总量为M,且M=qA+qB。
假设H2:博弈双方都有两种基本策略:竞争或打压策略(Hark)和合作策略(Dove)。竞争或打压策略。
假设H3:博弈双方都是理性经济行为体,以追求本国国际货币主导权福利最大化为决策目标,各国的国际货币供给量qi为关键决策变量。
假设H4:这是一个完全信息动态博弈,博弈分为两个阶段进行。守成大国A 首先决定其国际货币供给量qA;崛起大国B观测到qA后决定自己的国际货币供给量qB。
2. 国际货币主导权的福利函数
国际货币主导权的国家福利大小取决于其在全球国际货币供给总量的份额,福利来源于国际货币发行直接收益、国际货币主导权地位提升带来的附加收益和通过打压与竞争策略所获得的超额收益三方面。
第一,国际货币发行直接收益,包括两部分:一是直接的国际铸币税收入,即国际货币主导权国发行流通在国外的货币数量。假定一国流通在国外的货币数量占国际货币总量的比率为bi,那么该国的这部分铸币税收入Si=bi·M,其中0<bi<1,bi=qi/M。二是国际货币主导权国运用国外储备资产投资的收益与支付给国外储备资产所有者的回报之差,即进行金融运作获得净收益Fi=bi·M(rL-rS)。其中rS为国外储备资产回流购买该国国债或存款而支付的回报率,rL为该国运用这些回流资金进行投资获得的报酬率,且满足rL>rS。
第二,国际货币主导权地位附加收益,主要是国际货币主导权国凭借其在国际经济、贸易和金融方面绝对的优势地位所获得的间接收益。包括国际经济与贸易交易成本和汇率风险降低、融投资收益的提升等。同时也承担着本币升值、本国商品出口竞争力下降、资产价格泡沫增大、金融稳定和国际责任等成本。为此,文章综合考虑国际金融主导权地位的净收益,假定其为两国国际货币总量的二次凹函数Ai=c1(qi2+qi qj)+c2qi+c3,其中i,j分别表示国家i和国家j;c1,c2,c3为常数,满足c1<0,c2>0。
第三,一国通过打压或竞争手段,向国际市场投放更多的国际货币,以提高自身的国际货币市场份额而获得超额收益Ti=tiqi-tjqj,其中ti和tj为国家i和国家j对竞争对手的打压或竞争程度,满足ti≥0,tj≥0。
因此,一国国际货币主导权的总福利函数Wi表示为:

其中,λ 为国际货币主导权地位附加收益在总福利中的权重,λ>0;β 为打压与竞争策略获得的超额收益在总福利中的权重,β>0。
于是有,守成大国A 的国际货币主导权福利函数为:

公式(2)可简化为:

崛起大国B 的国际货币主导权福利函数为:
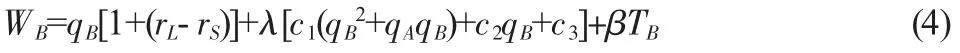
公式(4)可简化为:

3.大国国际货币主导权竞争的单次Stackelberg 博弈策略组合
在完全信息下进行一次博弈分析,博弈双方都能充分了解对手的策略及相应的收益,则守成大国与崛起大国基于国际货币主导权竞争的单次Stackelberg 博弈有四种策略组合。
(1) 第一种策略组合:守成大国和崛起大国都采取合作策略(D,D)
博弈双方都以保持自身福利最大化条件下的国际货币市场份额,无意采取措施挤压对方的国际货币市场空间。博弈双方都不会因为竞争与打压获得超额收益,即βTi=0。
此种情形下,守成大国的国际货币主导权福利函数为:

相应地,崛起大国的国际货币主导权福利函数为:

采用逆向归纳法求解这个博弈的子博弈精炼纳什均衡。首先求解第二阶段,给定qA的情况下崛起大国的最优选择,即崛起大国要实现:
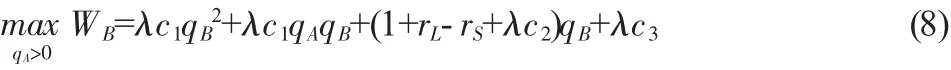

将式(9)代入式(6),求解在博弈第一阶段,守成大国的最优选择,即要实现守成大国:


将式(11)代入式(9)可得崛起大国的最优国际货币供给量为:

将式(11)和式(12)分别代入式(6)和式(7)可得在(合作,合作)策略组合情形下两个国家的福利分别为:
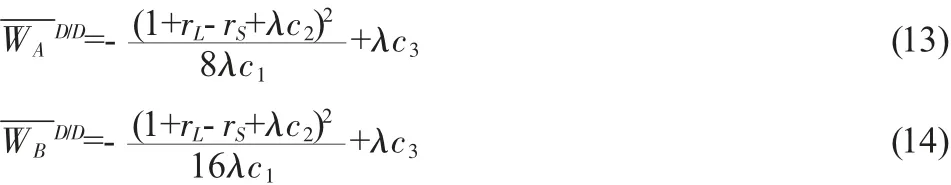
(2)第二种策略组合:守成大国采取合作策略,崛起大国采取竞争策略(D,H)
崛起大国为争取更多的国际货币市场份额而积极竞争,而守成大国默认崛起大国的竞争策略,那么崛起大国因为竞争而获得超额收益TB=tBqB,而守成大国则损失相应的福利。
此种情形下,守成大国的国际货币主导权福利函数为:

相应地,崛起大国的国际货币主导权福利函数为:

通过求解第二阶段崛起大国最优选择的一阶条件,即式(16)一阶导数等于零,可得崛起大国最优国际货币供给量qB对守成大国国际货币供给量qA的反应函数:

将式(17)代入式(15)求解第一阶段守成大国最优选择的一阶条件,即式(15)一阶导数等于零,可得此种策略组合下守成大国的最优国际货币供给量:

将式(18)代入式(17),可得均衡状态下崛起大国的国际货币供给量为:

把式(18)和(19)分别代入式(15)和(17)可得在此策略组合下两个国家的福利分别为:

(3) 第三种策略组合:守成大国采取打压策略,崛起大国采取合作策略(H,D)
守成大国先发制人打压崛起大国的国际货币市场地位,而崛起大国默认守成大国的打压策略。那么守成大国因为打压策略而获得超额收益TA=tAqA,而崛起大国则损失相应的福利。
此种情形下,守成大国的国际货币主导权福利函数为:

相应地,崛起大国的国际货币主导权福利函数为:

通过求解式(23)最大化的一阶条件等于零,可得此种策略组合下崛起大国最优国际货币供给量qB对守成大国国际货币供给量qA的反应函数:
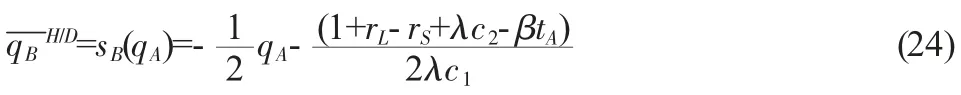
将式(24)代入式(22)可得此种策略组合下第二阶段守成大国的最优国际货币供给量为:

将此式代入式(24)可得均衡状态下崛起大国的国际货币供给量为:

由于崛起大国在世界经济增长、国际贸易等方面快速增长的影响,守成大国无法通过打压完全消除其不断提升的国际货币地位,即,1+rL-rS+λc2-2βtA>0。把式(25)和(26)代入式(22)和(23)可得在策略组合下两个国家的均衡福利为:
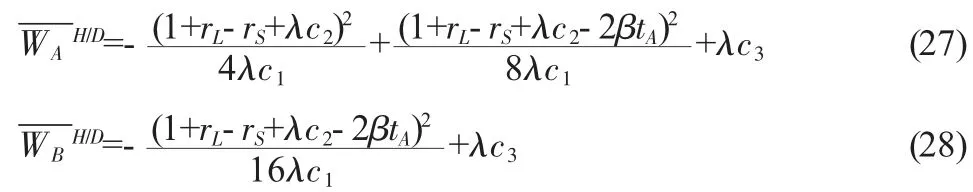
(4) 第四种策略组合:守成大国采取打压策略,崛起大国采取竞争策略(H,H)
守成大国打压崛起大国的国际货币市场地位,而崛起大国也积极竞争提升自身的国际货币市场地位,那么守成大国因为打压策略而获得收益TA,同时承受崛起大国竞争而带来的损失TB,最终获得超额收益为TA-TB;相应地,崛起大国获得的超额收益为TB-TA。
此种情形下,守成大国的国际货币主导权福利函数为:

相应地,崛起大国的国际货币主导权福利函数为:

通过求解满足式(30)最大化的一阶条件,可得崛起大国最优国际货币供给量qB对守成大国国际货币供给量qA的反应函数:

将式(31)代入式(29)可得在此策略组合下第二阶段守成大国的国际货供给量均衡为:

将式(32)代入式(31)可得均衡状态下崛起大国的国际货币供给量为:

将式(32)和(33)分别代入式(29)和(30)可得均衡状态下两个国家的福利为:
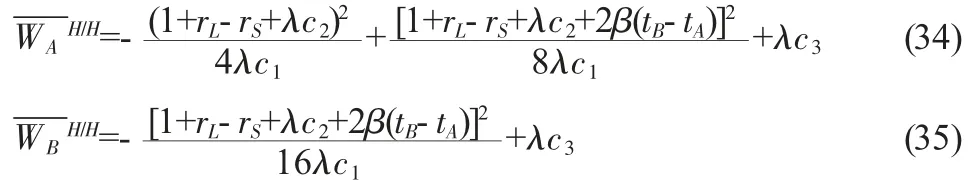
总结上述四种策略组合,可得大国国际货币主导权竞争Stackelberg 博弈的支付矩阵(见表1)。

表1 大国国际货币主导权竞争的Stackelberg 博弈支付矩阵
4. 大国国际货币主导权博弈的单次博弈均衡策略
为了更加直观地反映守成大国与崛起大国之间不同博弈策略组合下的收益情况,文章通过笛卡尔坐标系(图2) 来审视两国决策的推理过程。纵轴和横轴分别代表守成大国A 和崛起大国B 打压(竞争) 与合作的选择,四个象限分别代表该选择获得的收益。

图2 守成大国与崛起大国的博弈策略与福利横向与纵向比较
对于守成大国A:如果崛起大国B 采用合作策略,那么纵向比较第②、③象限的收益,比较过程如下:

因为C1<0,β<0,tA<0,则有,βtA>0;并且,
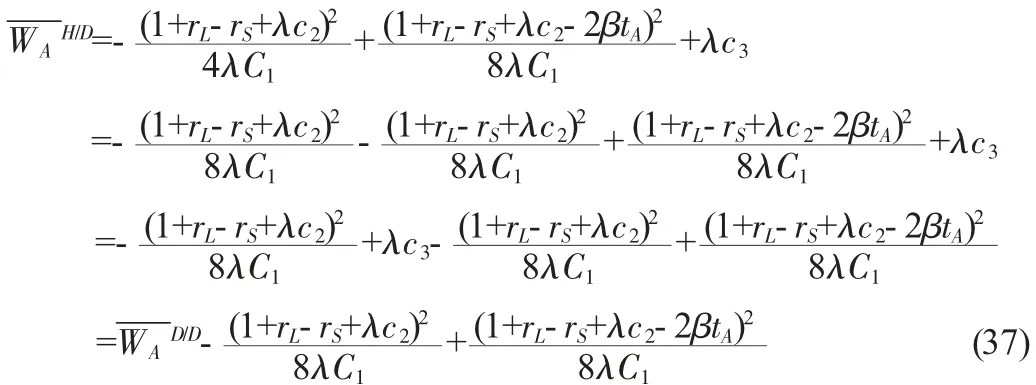
又因为βtA>0,那么(1+rL-rS+λc2)2>(1+rL-rS+λc2-2βtA)2,于是有≥0。
由此可知,如果崛起大国B 采用合作策略,守成大国A 应该选择打压策略;如果崛起大国B 选择竞争策略,通过纵向比较①、④象限的收益可知,守成大国也应该选择打压策略。可以看出,无论崛起大国B 选择合作策略还是竞争策略,对于守成大国A 而言,其选择打压策略的收益都高于合作策略的收益,打压策略是其占优策略。
同理,对于崛起大国B:如果守成大国A 选择合作策略,那么通过横向比较①、②象限的收益可知,应该选择竞争策略;如果守成大国A 选择打压策略,通过横向比较③、④象限的收益可知,也应该选择竞争策略。无论守成大国A 选择打压策略还是合作策略,竞争策略都是崛起大国B 的占优策略。
在单次Stackelberg 博弈中,无论对于守成大国A 还是崛起大国B 来说,打压或竞争策略要优于合作策略,博弈的唯一均衡解就是(打压,竞争) 策略组合,这是典型的“囚徒困境”博弈结果。这一博弈的子博弈精炼纳什均衡是在每一个过程中博弈双方都不合作,但博弈双方如果都选择合作战略,根据图3,斜向比较②、④象限的收益可知,(合作,合作) 的福利水平高于(打压,竞争) 的福利水平。

图3 守成大国与崛起大国的博弈策略与福利斜向比较
但是,当参与博弈的其中一方选择合作策略时,另一方有动机选择打压或竞争策略。因为这样其可以获得高于双方都选择合作策略的水平,而且选择合作策略的一方也十分清楚对方存在的这种动机,最终结果是双方都选择打压或竞争策略,即博弈双方个体的理性行为选择实现资源次优配置的策略,而不是实现福利最大化的帕累托最优策略。这属于典型的个体理性与集体理性悖论的囚徒困境博弈。
三、大国国际货币主导权竞争的重复博弈及其均衡策略
Kreps 等(1982)论证得出,如果赋予博弈双方采取“以牙还牙”策略一定的预期概率,在足够长的有限时期里,双方一定存在合作的情形[9]。Robert Axelrod(2006)实验证明,单次博弈下不合作的囚徒困境将会被重复博弈下有条件合作的占优策略所破解[10]。大国国际货币主导权单次博弈的囚徒困境也可以通过重复博弈促使双方实现合作。
1.大国国际货币主导权博弈的有限次重复博弈及其纳什均衡
假定守成大国A 与崛起大国B 将单次博弈重复n次(n≥2),博弈双方在每次重复博弈中所掌握的信息、博弈规则和行动次序与单次博弈的完全一样。那么博弈双方有限次重复博弈的均衡解仍可采用逆向归纳法进行求解。博弈双方都知道第n次是最后一次博弈,博弈双方的选择跟单次博弈一样,选择打压或竞争策略是他们的占优策略,其策略组合为(打压,竞争),双方的收益为。在第n-1 次博弈中,因为已知第n次博弈彼此的策略选择,此次博弈不会对第n次博弈产生任何影响,双方同样都会选择打压或竞争策略,即策略组合仍为(打压,竞争)。直到第一次博弈,博弈双方都这样选择。因此,大国国际金融主导权竞争的有限制重复博弈的纳什均衡策略组合仍是(打压,竞争),没有破解囚徒困境。
2.大国国际货币主导权博弈的无限次重复博弈及其纳什均衡
实际上,守成大国A 与崛起大国B 之间是一个长期动态的博弈过程,根本就没有所谓的最后一次。所以可以将有限重复博弈次数改为无限次(n→∞),这样守成大国A 与崛起大国B 之间的重复博弈就是一个无法已知博弈结束点的无限次重复博弈。因此,不能继续用逆向归纳法进行求解。
在守成大国A 与崛起大国B 之间的单次博弈和有限次重复博弈中,博弈双方仍然陷入囚徒困境的主要原因是,缺乏在自己选择合作策略时促使对方也采用合作策略的保障机制。在无限次重复博弈中,由于博弈双方知道彼此将长期博弈,并且不知道或者根本就没有结束点,那么从心理上都倾向于争取长期利益。如果博弈双方要实现互利互惠的均衡,双方都应试图选择合作并且要惩罚对方的不合作(即打压或竞争)。如果自己选择合作策略,而对方选择不合作策略,那么自己在下一轮博弈中也会选择不合作策略,并且之后会一直选择不合作策略,通过这种方式来惩罚不合作者,这叫作冷酷策略。在守成大国A 与崛起大国B 的无限次重复博弈中,冷酷策略是对其的最优反应。
3. 破解大国国际货币主导权博弈囚徒困境的奖惩机制
在大国国际货币主导权的无限次重复博弈中,博弈双方的冷酷策略促使双方进行合作,本质上就是建立一种奖惩机制。惩罚选择不合作的博弈大国,且惩罚带来的损失大于不合作所产生的超额利益;奖励选择合作的博弈大国,使该奖励带来的收益大于遭受背叛的损失;博弈双方,参与者的理性会使其追求利益最大化,进而彼此都选择合作策略。这种奖惩机制可以是博弈双方签订的一个合约,也可以是博弈参与方单方面设计的机制,提前明确告知对方,并且确保这种奖惩的可信度。
美国与英国在20 世纪30—40 年代的博弈,能够由囚徒困境转化为合作博弈,其中非常重要的原因是,美国建立了奖励合作和惩罚不合作的博弈机制。美国构建的奖惩机制,简言之就是以利诱之,以威慑之,逼其就范;这在国际上被形象地称为“胡萝卜”加“大棒”策略组合。这也是美国作为当今国际货币主导权的守成大国频频挥舞金融制裁大棒的一个重要原因,对于任何不遵守由其主导的国际货币金融规则的国家或个体就会立即对其进行严重的金融制裁予以惩罚。不难发现,不论是崛起大国日本、欧盟还是现在的中国,总体上在与美国的国际货币主导权博弈中虽然斗争不断,但合作仍为主线。
四、大国国际货币主导权博弈的数值仿真
为了更好理解守成大国A 与崛起大国B 之间基于国际货币主导权的博弈行为,分析双方如何选择博弈策略,以及决策如何影响自身利益与对方收益及行为,在此基于大国国际货币主导权博弈的Stackelberg 博弈模型的四种策略组合进行数值仿真。有关参数赋值如下:rL=0.1,rs=0.05,λ=0.6,c1=-2.0,c2=0.7,c3=2,β=0.5,tA=0.5,tB=0.3,得到四种策略组合的均衡解如表2 所示:

表2 基于Stackelberg 模型的大国国际货币主导权博弈数值仿真的均衡解
1. 大国国际货币主导权博弈囚徒困境结果的证实
2. 不同策略下博弈大国双方的国际货币市场份额与福利水平
不同策略下守成大国A 的国际货币市场份额与福利水平如图4 所示。无论哪种策略组合,守成大国A 的国际货币市场份额qA=0.6125 保持不变,这也意味着单次博弈,无论博弈双方采取合作还是竞争策略,都不能改变守成大国国际货币市场份额,却能改变其福利水平。当崛起大国采取合作策略,守成大国采用打压策略时的福利水平最高;当崛起大国采用竞争策略而守成大国采用合作策略时的福利水平最低,所以对守成大国而言采取打压策略是最有利可图的,这也正是守成大国不惜一切代价打压崛起大国争夺国际货币主导权的根本利益动因。
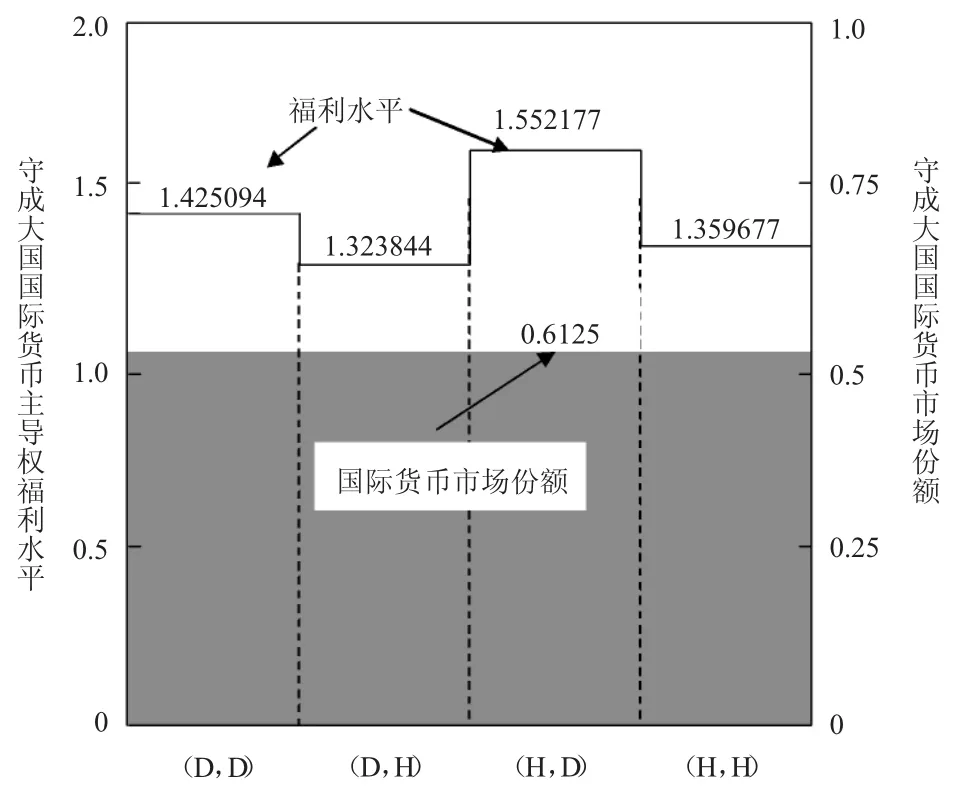
图4 不同策略下守成大国A 的国际货币市场份额与福利水平
不同策略下崛起大国B 的国际货币市场份额与福利水平如图5 所示。当守成大国采用合作策略,崛起大国采用竞争策略时其国际货币市场份额最高,并且其福利水平也最高;当守成大国采用打压策略,而崛起大国采用合作策略时,其国际货币市场份额和福利水平最低。可见,对于崛起大国而言,同样采用竞争策略是最有利可图的;另外,崛起大国的国际货币市场份额与策略组合相关,并直接决定其福利水平的高低,这与守成大国其国际市场份额不变有所不同。这表明,对于崛起大国而言要争夺国际货币主导权最首要的就是争夺国际货币市场份额,这也是崛起大国积极推动本国货币国际化的重要原因。

图5 不同策略下崛起大国B 的国际货币市场份额与福利水平
五、主要结论及对中美博弈的对策建议
文章的主要结论是:在大国国际货币主导权的单次博弈和有限次重复博弈中,打压或竞争是博弈双方的占优策略,博弈双方陷入囚徒困境;在无限次重复博弈中,都会采取“以牙还牙”的冷酷策略,让合作成为彼此的最优选择,进而破解囚徒困境;要促使双方的博弈关系由竞争转向合作,必须设计合理的奖惩机制。数值仿真结果论证了大国主要通过争夺国际货币市场份额进而争夺国际货币主导权的大国博弈逻辑关系,并且守成大国与崛起大国之间打压与竞争的攻防博弈是常态。
对于中美基于国际货币主导权的大博弈,如何避免陷入囚徒困境,提出以下建议。首先,必须清晰地认识到中美大博弈尚处于早期蓄势阶段。中国作为新兴崛起大国与守成大国美国还有很大的差距,最重要的是需要不断增强自身综合实力和发展能,提升国际主导地位。其次,积极争取与国力相应的国际货币主导权,深入推进货币金融体制改革,打造具有国际竞争力的航母级金融机构,建立开放型金融市场体系,完善金融治理体系。最后,尊重美国国际货币主导权地位,同时坚决反对其货币霸权行为,坚持共商共建共享的全球治理观,积极推动国际货币金融治理体制变革,构建全球金融利益共同体,扩大合作领域,增强合作动力。
