SZEGÖ KERNEL FOR HARDY SPACE OF MATRIX FUNCTIONS∗
2016-04-18FuliHE贺福利SchoolofMathematicsandStatisticsCentralSouthUniversityChangsha410083ChinaEmailhefuli999163comMinKU库敏UweHLERCIDMADepartmentofMathematicsUniversityofAveiroPortugalEmailkumin0844163comukaehleruapt
Fuli HE(贺福利)School of Mathematics and Statistics,Central South University,Changsha 410083,ChinaE-mail:hefuli999@163.comMin KU(库敏)Uwe KÄHLERCIDMA,Department of Mathematics,University of Aveiro,PortugalE-mail:kumin0844@163.com;ukaehler@ua.pt
SZEGÖ KERNEL FOR HARDY SPACE OF MATRIX FUNCTIONS∗
Fuli HE(贺福利)
School of Mathematics and Statistics,Central South University,Changsha 410083,China
E-mail:hefuli999@163.com
Min KU(库敏)†Uwe KÄHLER
CIDMA,Department of Mathematics,University of Aveiro,Portugal
E-mail:kumin0844@163.com;ukaehler@ua.pt
AbstractBy the characterization of the matrix Hilbert transform in the Hermitian Clifford analysis,we introduce the matrix Szegö projection operator for the Hardy space of Hermitean monogenic functions de fined on a bounded sub-domain of even dimensional Euclidean space,establish the Kerzman-Stein formula which closely connects the matrix Szegö projection operator with the Hardy projection operator onto the Hardy space,and get the matrix Szegö projection operator in terms of the Hardy projection operator and its adjoint.Furthermore,we construct the explicit matrix Szegö kernel function for the Hardy space on the sphere as an example,and get the solution to a boundary value problem for matrix functions.
Key wordsHardy space;Hermitean Clifford analysis;Szegö projection;matrix function
2010 MR Subject Classi fication30G35;15A66;30C40;31A25;31B10
∗Received October 6,2014;revised March 12,2015.The project is supported by Portuguese funds through the CIDMA Center for Research and Development in Mathematics and Applications,and the Portuguese Foundation for Science and Technology(FCT-Funda¸cão para a Ciênciae a Tecnologia)within project UID/MAT/04106/2013 and by NNSF of China(11371375,11301547).The corresponding author is the recipient of a Postdoctoral Foundation from FCT under Grant No.SFRH/BPD/74581/2010.
†Corresponding author:Min KU.
1 Introduction
The Szegö kernel function(for short Szegö kernel)and the Szegö projection,which were fi rst introduced by the Hungarian mathematician Gábor Szegö in 1921(see ref.[1]),played an important role in the development of the complex analysis.The Szegö kernel is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions de fined on a domain(see refs.e.g.[2,3]),which is of importance to reveal the properties of the holomorphic map between two domains and to solve the boundary value problems.For instance,the conformal mappings onto the canonical domains,the classical functions,and other important objects of potential theory can be simply expressed in virtue of the Szegö kernels(seen in refs.e.g.[3-5]).The Szegö projection operator associates with smooth boundary of a domain is of fundamental interest in the complex analysis.Its action can often be expressed as an integration againsta distribution,known as the Szegö kernel,and the study of its is naturally introduced for the space of square integrable function onto Hardy space de fined on the boundaries of a domain(see refs.e.g.[1,3]).This allows us to deeper understand the geometric and functional analytic properties in the complex analysis and the harmonic analysis(see refs.e.g.[2,3]).
However,it is not feasible to obtain the closed formulas of the Szegö kernels for the general domains of the complex plane.One of the difficulties lies in that one could not obtain an estimation for these kernels in terms of the geometrical properties of the considered domains.Only for the special cases,including the unit circle,the Szegö kernels can be computed explicitly.Moreover,it is showed by Kerzman and Stein in ref.[2]that the unit circle is the only planar region,for which the Szegö kernel and the Cauchy kernel coincide.On the contrary,for the general domains on the complex plane,they established the well-known Kerzman-Stein formula(see refs.e.g.[2,3]),which connects the Szegö projection with the Hardy projection.Later on,in refs.[6-8],Bernstein,Calderbank,Delanghe and their collaborators generalized the Kerzman-Stein formula to the higher dimensions,making full use of the methods of the orthogonal Clifford analysis,seen in Refs.e.g.[12-19].More related results on the Szegö kernel and the Szegö projection in the orthogonal Clifford analysis can be also found in refs.e.g.[9-11].
O ff ering a re fi nement of the orthogonal case,the Hermitean Clifford analysis,seen in refs.e.g.[20-24],emerged as a new and successful branch of Clifford analysis.It focuses on the simultaneous null-solutions of the two complex Hermitean Dirac operators,which recently invokes new tools for the study of circulant(2×2)matrix functions.A Cauchy integral formula in the Hermitean Clifford was constructed in terms of circulant(2×2)matrix functions(see refs.e.g.[25-28]),and the relationship with holomorphic function theory of several complex variables was observed,seen in refs.e.g.[24-26].The Hermitean Cauchy transform,which gave rise to the Hardy projection to be skew,and the related decomposition problems of continuous functions were discussed in refs.[27,28].The new Hilbert-like matrix operator was revealed by the non-tangential boundary limits of the Hermitean Cauchy transform in refs.e.g.[25,26].Much recent progress can be also seen in refs.[29,30]or elsewhere.Under this setting it is natural for us to want to know what is the matricial Szegö projection.But,to our knowledge,little attention is devoted to up to now.This leads us to further consider the Hardy space for circulant(2×2)matrix functions.In the underlying paper,based on refs.[2,6,26,30],we will first de fine a proper inner product on the space of square integral circulant(2×2)matrix functions de fined on the boundary of a bounded sub-domain in even dimensional Euclidean space,and introduce the matrix Szegö projection operator to be orthogonal for the Hardy space of Hermitean monogenic functions de fined on a bounded sub-domain of even dimensional Euclidean space.Then we will establish the Kerzman-Stein formula,which is closely related to the matrix Szegö projection operator and the Hardy projection operator onto the Hardy space of Hermitean monogenic functions de fined on a bounded sub-domain,and present the matrix Szegö projection operator in terms of the Hardy projection operator and its adjoint,explicitly.Lastly,we will give the explicit matrix Szegö kernel function for the Hardy space on the sphere.As an application,we get the solution to a boundary value problem for matrix functions.
The paper is organized as follows.In Section 2,we recall some basic facts about Hermitean Clifford analysis which will be needed in the sequel.In Section 3,we will introduce the matrixSzegö projection operator for the Hardy space of Hermitean monogenic functions de fined on a bounded sub-domain,establish the Kerzman-Stein formula which closely connects the matrix Szegö projection operator,and present the matrix Szegö projection operator in terms of the Hardy projection operator and its adjoint in the Hermitean Clifford setting.At last we will construct the explicit matrix Szegö kernel function for the Hardy space,and get the solution to Hermitean Dirichlet problem.
2 Preliminaries
In this section we recall some basic facts about Clifford algebra and Hermitean Clifford analysis which will be needed in the sequel.More details can be also seen in refs.e.g.[20-24].
Let(e1,···,em)be an orthogonal basis of Euclid space Rm,the complex Clifford algebra Cm,which is constructed over Rm,its geometric multiplication is governed by the rules ejek+ ekej=−2δjk,j,k=1,···,m.The Cmthus is generated additively by elements of the form eA=ej1···ejk,where A={j1,···,jk}⊂{1,···,m},j1<···<jk,while for A=∅,one puts e∅=1,the identity element.Any Clifford number a in Cmmay thus be written asand its Hermitean conjugate a†is de fined bywhere the bar denotes the usual real Clifford algebra conjugation anddenotes the standard complex conjugation.The Euclidean space Rmis embedded in Cmby identifying(x1,x2,···,xm)with the Clifford vectorNote that the square of a vectoris scalar valued and equals the norm squared up to a minus signThe Fischer dual of the vectoris the vector valued first order differential operatoris called Dirac operator.It is precisely this Dirac operator which underlies the notion of monogenicity of a function,a notion which is the higher dimensional counterpart or holomorphy in the complex plane.As the Dirac operator factorizes the Laplacian,monogenicity can be regarded as a re fi nement of harmonicity.
Hereby,introducing Hermitean Clifford analysis is based on the so-called almost complex structure on it,i.e.,an SO(m)-element J,satisfying J2=−1m.This forces the dimension m to be even,whence from now on,we will put m=2n.In terms of our basis,a particular realization of the almost complex structure is given by J(e2j−1)=−e2jand J(e2j)=e2j−1,j=1,···,n.
The real Clifford vector and the Dirac operator are denoted by

as well as their counterparts
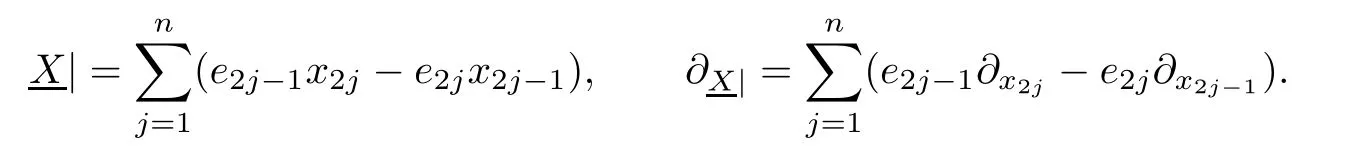
The Hermitean Clifford variables Z and Z†then given by

which satisfy
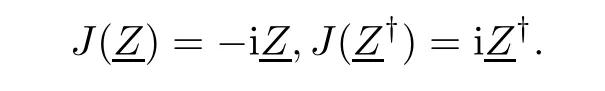
Hermitean Clifford analysis then focuses on simultaneous null solutions of two Hermitean Dirac operatorsintroduced by
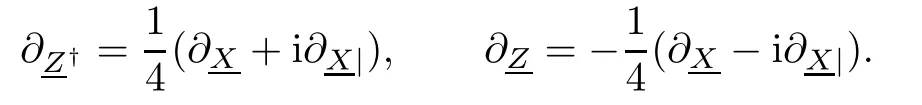
The fundamental solutions of the Dirac operators∂X,∂X|are

where ω2ndenotes the surface area of the unit sphere in R2n.We introduce

For further use,we introduce the oriented surface elements dσZand dσZ†by


We denote the outward pointing unit normal vector atfor the element on∂Ω,leading to
In this context the functions under consideration are de fined on an open subset Ω of R2nand take values in the Clifford algebra C2n.They are of the form f=∑AfAeA,where the functions fAare complex-valued.Whenever a property such as continuity,differentiability,Lpintegrable and so forth is ascribed to f,it is meant that all the components fApossess the cited property.Let g1,g2be C2n-valued functions de fined in Ω⊂R2n,we consider the corresponding circulant(2×2)matrix function in the following
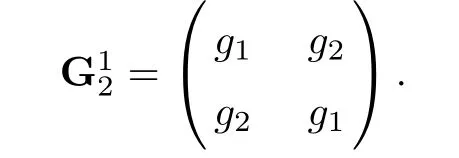
In what follows,the operations of matrices such as addition and multiplication,and the operations between the complex numbers and the matrices,respectively,keep to the operation rules of the usual numerical matrices and of multiplication between the complex numbers and the usual numerical matrices.Let Ω⊂R2nbe a bounded sub-domain with smooth boundary∂Ω.Functions taking values in C2nde fined on Ω∪∂Ω will be considered.Notions of continuity,differentiability and integrability of G12are introduced entry-wise.For instance,the circulant(2×2)matrix function G12∈Ck(Ω,C2n),Hµ(Ω,C2n),Lp(Ω,C2n)and so on which mean each entry of G12belongs to Ck(Ω,C2n),Hµ(Ω,C2n),Lp(Ω,C2n)and so on.We introduce the particular circulant(2×2)matrices

where δ is the Dirac delta distribution in R2n,theni.e.,ε is the fundamental solution of D(Z,Z†)(see refs.e.g.[20-24,26]).
For gi∈Lp(∂Ω,C2n),1<p<+∞,i=1,2,we de fi ne the orthogonal Cauchy type integrals as
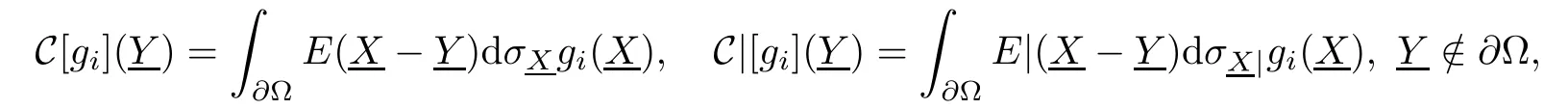
which are well-de fined(see refs.e.g.[12,13]),where E(X),E|(X)and dσX,dσX|as above.Then for


where

3 Szegö Projection Operator
In this section we will introduce the matrix Szegö projection operator for the Hardy space of Hermitean monogenic functions de fined on a bounded sub-domain,establish the Kerzman-Stein formula,and present the matrix Szegö projection operator in terms of the Hardy projection operator and its adjoint,explicitly.
Inspired by the inner product〈·,·〉L2on L2(∂Ω,C2n),given by

where[·]0denotes the scale part of any·in C2n.We introduce the following bi-linear form on the vector space L2(∂Ω,C2n)

Then,by directly calculating,for arbitraryand λ∈C,we can check that
Thus,〈·,·〉L2is a inner product,which derives the norm on L2(∂Ω,C2n)by

Hence,(L2(∂Ω),‖·‖)is the Hilbert space,which is different from the space of L2(∂Ω)in refs.e.g.[26,30].Under this setting,we have the following lemma without proof,which was also stated in[24,26,30]in the sense of different topology.For convenience without confusion and ambiguity,(L2(∂Ω),‖·‖)still denotes by L2(∂Ω).
Lemma 3.1Let Ω be a non-empty,open and bounded subset of R2nwith smooth boundary∂Ω.is de fined similarly to(1<p<+∞),then,for arbitrary T∈∂Ω,
where the limits of(ii)mean the non-tangential limits,which is the same in the following context,

and
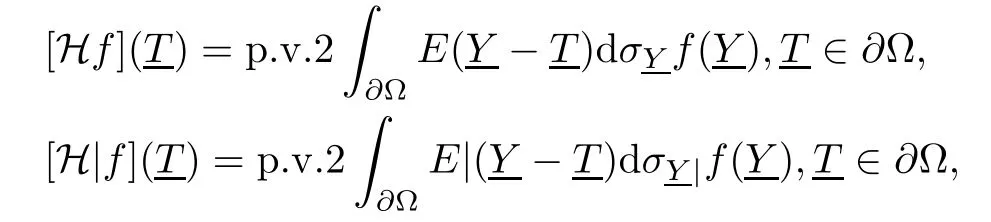
which are both Cauchy principle value integrals in the sense of Lp(1<p<+∞).When the variables are omitted without confusion and ambiguity,for convenience[Hf](T),[H|f](T)are for short of Hf,H|f,respectively,and it is also similar in the following context.
we will consider the Hardy space
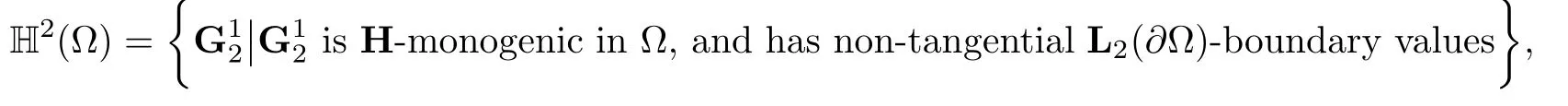
and H2(∂Ω)denotes the L2(∂Ω)-closure of the set of boundary values of elements of H2(Ω).
Remark 3.2Associating the Hardy space with(ii)of Lemma 3.1,the Hermitean Cauchy transform C maps L2(∂Ω,C2n)onto H2(∂Ω)for arbitrarywhich is skew and so-called the Hardy projection.
Associating the de finition of the above C-valued inner product on L2(∂Ω),we have the following lemma which is only stated without proof.
Lemma 3.3Suppose that H,L2(∂Ω)and H2(∂Ω)as Lemma 3.1 and Remark 3.2.Then
(i)H2=I,
where I denotes(2×2)identity matrix operator,H∗means the adjoint operators of H on L2(∂Ω)and
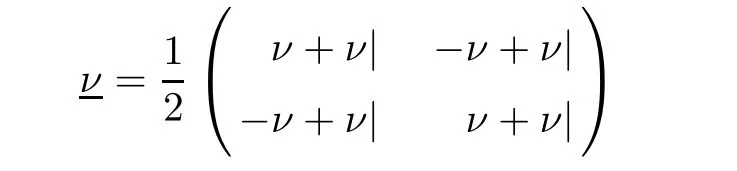
with ν being the outward pointing unit normal vector at X∈∂Ω and J(ν)=ν|.
Remark 3.4The results similar to Lemma 3.3 were also mentioned in refs.[24,26]with respect to(C2n)2×2-valued inner product,which does not derive a norm and is different from our C-valued inner product on L2(∂Ω).
Starting with(ii)of Lemma 3.3,the matrix orthogonal projection operator S from L2(∂Ω)onto H2(∂Ω),which is so-called the matrix Szegö projection operator,may be Hermitean monogenically extended to H2(Ω)by
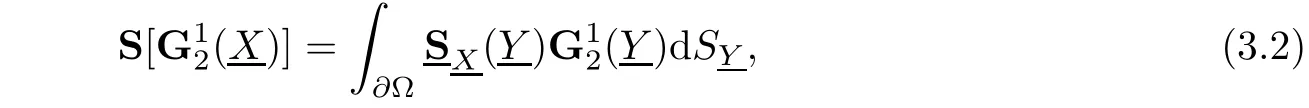

Remark 3.5Particularly,when Ω=B(1)the unit ball centered at 0 of R2n,∂Ω=S2nthe unit sphere of R2nand
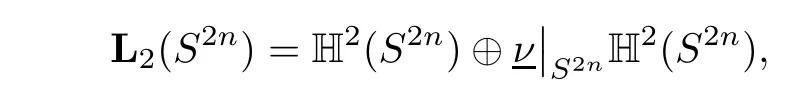
where

We consider the Dirichlet problem as follows,given the boundary datafind the functionsuch that

where

It is easy to verify that(3.3)is equivalent to the system

In virtue of(iv)in Lemma 3.3,we have

Then the above Dirichlet problem(3.3)exists the unique solution.Moreover the solution is formulated in the following form
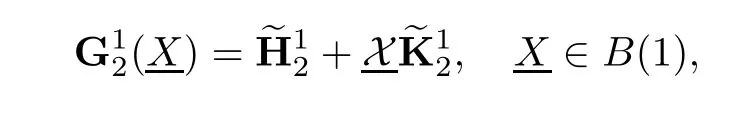

In what follows,we introduce the matrix Kerzman-Stein operator on y2(∂Ω)by
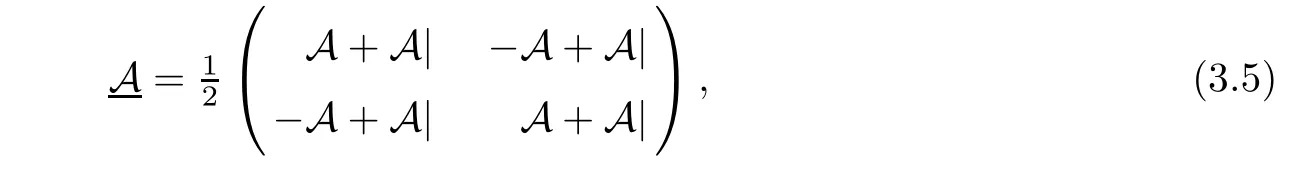
where
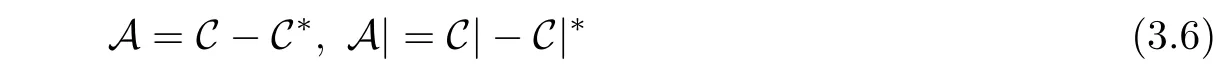
are both well-de fined,C∗and C|∗denote the adjoint operators of C and C|on the Hilbert space of L2(∂Ω,C2n),respectively,given by
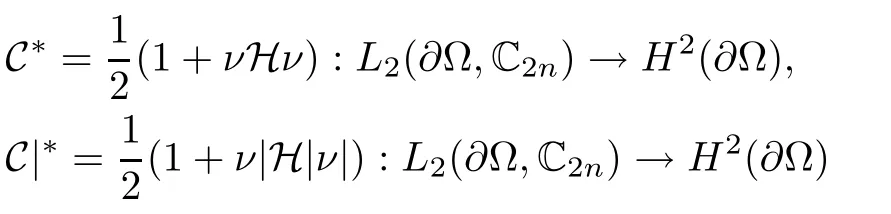
with H2(∂Ω)being L2(∂Ω,C2n)-closure of the set of boundary values of elements of

ν,ν|,H,H|as Section 2,and 1 being the identity operator.More detail can be seen in refs.[10-12].
Applying Lemma 3.3,we directly get the following lemma.
Lemma 3.6Let A and A|be as term(3.6),and C be as Remark 3.2.Then

where H∗,seen in Lemma 3.3,andmean the adjoint operators of H and C on L2(∂Ω).
Theorem 3.7Let S be as term(3.2),and C be as Remark 3.2.Then

where I denotes(2×2)identity matrix operator.
ProofSince the matrix operator S is orthogonal projection operator on the Hilbert space L2(∂Ω),S=S∗.Noticing that the operators S and C are orthogonal and skew projection operators from L2(∂Ω)to H2(∂Ω),respectively,then SC and CS are both operators from L2(∂Ω)to H2(∂Ω).In particular,operators S and C are both the identical operators on H2(∂Ω),respectively.Therefore,we have

Applying the property of the adjoint operator on the Hilbert space of L2(∂Ω)(see refs.e.g.[3,10,12]or monographs of functional analysis),(SC)∗is well-de fined and(SC)∗=C∗S∗,where C∗means the adjoint operator of C acting on L2(∂Ω).Taking the adjoint operators with respect to〈·,·〉L2,we have

Hence,associating terms(3.9)with(3.10),we get

Therefore,one has

Thus,the proof of the result is complete.
Remark 3.8Theorem 3.7 characterizes the relationship between Hermitean Hardy projection operator and matrix Szegö projection operator,which is the generalization of the wellknown Kerzman-Stein formula into the setting of Hermitean Clifford analysis.
We de fi ne the matrix operator as follows
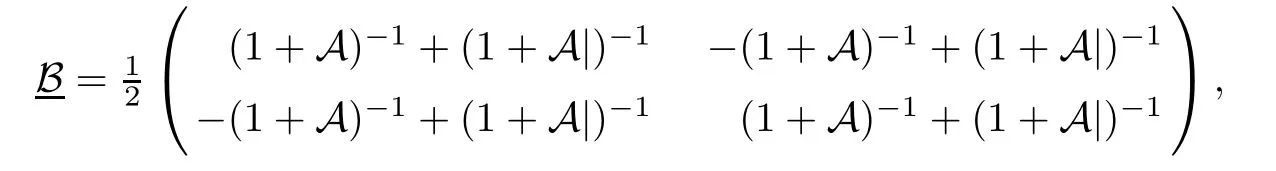
where 1 denotes the identity operator on L2(∂Ω,C2n).
Observing from term(3.6),the operators 1+A and 1+A|are invertible on L2(∂Ω,C2n),which could be also seen in Lemma 4.5 in[6]or[3],the matrix operator B is well de fined on L2(∂Ω).
Theorem 3.9Let S and C be as Theorem 3.7.Then the matrix Szegö projection operator is explicitly formulated by

where I denotes(2×2)identity matrix operator.
ProofApplying term(3.7),we know that operatoris anti-self conjugate.This implies that the spectra of operator A are pure imaginary numbers.Hence,operatoris invertible.Moreover,by calculating directly,we get(I+A)−1=B.It follows the result.
Remark 3.10Equation(3.11)is our basic desired formula,which gives a characterization of the matrix Szegö projection operator.Notice that,for smooth boundary of a bounded domain,the principal value parts in C−C∗have disappeared,which leads to the inverse of operator A.For smooth boundary of general unbounded domains,it is more complicated,which we do not focus on.
4 Szegö Kernel
In this section we construct the explicit matrix Szegö kernel for the Hardy space H2(S2n).As an application of it,we get the solution to a boundary value problem for matrix functions in terms of integral formula.
We introduce the functions


where K=−(K+iK|),K†=K−iK|.
ProofNoticing,for arbitrary Y,Y|∈S2n,

we have

Then we get
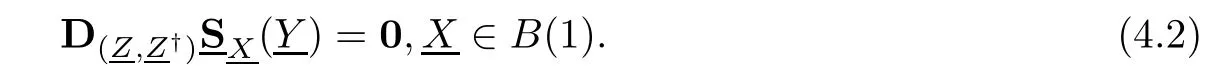
Applying the Cauchy formula in[20,26],for arbitrarywe have
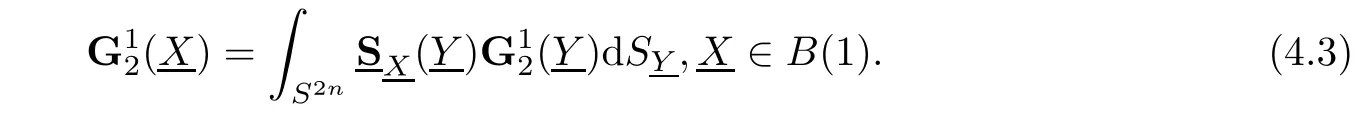
Remark 4.2Let S=CnI denote the spinor space,where I=I1···Inis the primitive identity element withand the Grassmann algebra1,2,···,n generated by the Witt basisref.e.g.[26]).Whenwith g taking values in the homogeneous n-space of spinor space Sn,i.e.,g(z1,···,zn)=gn(z1,···,zn)with gn(z1,···,zn)being complex valued function de fined in R2n~=Cn,then by direct calculation,term(4.3)induces to the term as follows
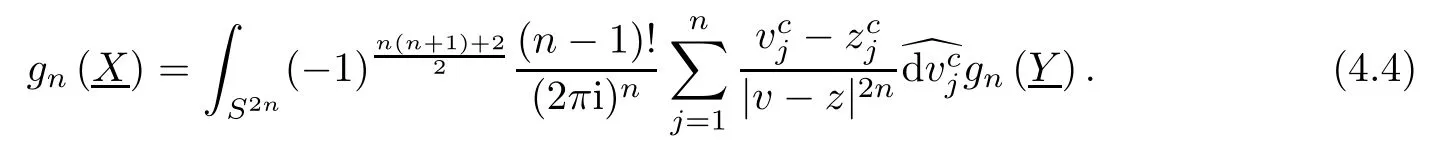
This implies that the matrix Szegö kernelreduces to the Martinelli-Bochner kernel
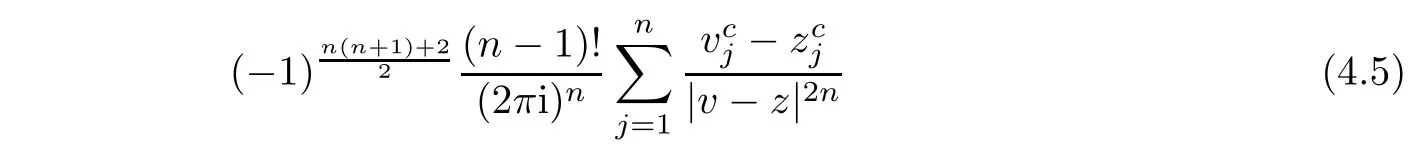
of holomorphic functions of several complex variables on the unit ball,where

Furthermore,if n=1,term(4.5)is equal to the case
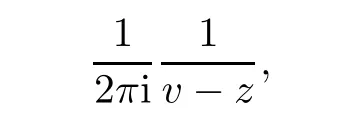
As an application of the matrix Szegö kernel,we get the theorem as follows.

ProofApplying Lemma 3.3,associating with Theorem 3.11,it follows the result.
Remark 4.4Hereby,we only present the explicit solution of the classical Dirichlet problem on the ball of higher-dimensional space,by means of the matrix Szegö kernel.In fact,this leads the decomposition of the classical matrix Poisson kernel by

where

Following the same argument,we could consider the Dirichlet problem for matrix functions on the general sub-domains of higher-dimensional space,which will be discussed in the forthcoming paper.
References
[1]Szego G.Über orthogonale polynome,die zu einer gegebenen Kurve der komplexen Ebene Gehören.Math Z,1921,9:218-270
[2]Bell S.The Cauchy Transform,Potential Theory and Conformal Mapping.Boca Roton:CRC Press,1992
[3]Kerzman N,Stein E M.The Cauchy kernel,the Szegö kernel and the Riemann mapping function.Math Ann,1971,236:85-93
[4]Bell S.Solving the Dirichlet problem in the plane by means of the Cauchy integral.Indiana Univ Math J,1990,39(4):1355-1371
[5]Bell S.The Szegö projection and the classical objects of potential theory in the plane.Duke Math J,1991,64(1):1-26
[6]Bernstein S,Lanzani L.Szegö projections for Hardy spaces of monogenic functions and applications.Int J Math Math Sci,2002,29:613-624
[7]Calderbank D.Clifford Analysis for Dirac Operators on Manifolds with Boundary.Bonn:Max-Planck-Institute Für Mathematik,1996
[8]Delanghe R.On some properties of the Hilbert transform in Euclidean space.Bull Belg Math Soc Simon Stevin,2004,11:163-180
[9]Constales D,Krausshar R S.Szegö and polymonogenic Bergman kernels for half-space and strip domains,and single-periodic functions in Clifford analysis.Complex Var Elliptic Equ,2002,47(4):349-360
[10]Delanghe R,Brackx F.Hypercomplex function theory and Hilbert modules with reproducing kernel.Proc London Math Soc,1978,37(3):545-576
[11]Ryan J.Complexi fied Cliff ord analysis.Complex Var Theory Appl,1982,1(1):119-149
[12]Brackx F,Delanghe R,Sommen F.Clifford Analysis.London:Pitman,1982
[14]Gürlebeck K,Sprössig W.Quaternionic and Cliff ord Calculus for Physicists and Engineers.Chichester,New York:Wiley,1997
[15]Gilbert J E,Murry M A M.Cliff ord Algebra and Dirac Operators in Harmonic Analysis.Cambridge Studies in Advances Mathematics 26.Cambridge:Cambridge University Press,1991
[16]McIntosh A.Clifford algebras,Fourier transforms,and singular convolution operators on Lipschitz surfaces.Rev Mat Iberoamericana,1994,10(3):665-721
[17]Ku M,Du J Y.On integral representation of spherical k-regular functions in Cli fford analysis.Adv Appl Clifford Alg,2009,19(1):83-100
[18]Ku M.Integral formula of isotonic functions over unbounded domain in Clifford analysis.Adv Appl Clifford Alg,2010,20(1):57-70
[19]Ku M,Du J Y,Wang D S.On generalization of Martinelli-Bochner integral formula using Clifford analysis.Adv Appl Clifford Alg,2010,20(2):351-366
[20]Brackx F,et al.Fundaments of Hermitean Clifford analysis.I.Complex structure.Complex Anal Oper Theory,2007,1:341-365
[21]Brackx F,et al.Fundaments of Hermitean Clifford analysis.II.Splitting of h-monogenic equations.Complex Var Elliptic Equ,2007,52(10/11):1063-1079
[22]Rocha-Chavez R,Shapiro M,Sommen S.Integral theorems for functions and differential forms in Cm//Research Notes in Mathematics 428.New York:Chapman Hall/CRC,2002
[23]Brackx F,De Schepper H,Sommen F.The Hermitian Clifford analysis toolbox.Adv Appl Clifford Alg,2008,18:451-487
[24]Brackx F,De Knock B,De Schepper H,Sommen F.On Cauchy and Martinelli-Bochner integral formulae in Hermitean Clifford analysis.Bull Braz Math Soc,2009,40(3):395-416
[25]Brackx F,De Knock B,De Schepper H.A matrix Hilbert transform in Hermitean Clifford analysis.J Math Anal Appl,2008,344:1068-1078
[26]Ku M,Wang D S.Half Dirichlet problem for matrix functions on the unit ball in Hermitean Clifford analysis.J Math Anal Appl,2011,374:442-457
[27]Abreu Blaya R,Bory Reyes J,Moreno Garc´ıa T.Hermitian decomposition of continuous functions on a fractal surface.Bull Braz Math Soc,2009,40(1):107-115
[28]Abreu Blaya R,Bory Reyes J,Brackx F,De Knock B,De Schepper H,Peña Peña D,Sommen F.Hermitean Cauchy integral decomposition of continuous functions on hypersurfaces.Boundary Value Problems,2008,2008:Article ID 425256
[29]Eelbode D,He F L.Taylor series in Hermitean Clifford analysis.Complex Anal Oper Theory,2011,5(1):97-111
[30]Ku M,Kähler U,Wang D S.Half Dirichlet problem for the Hölder continuous matrix functions in Hermitian Clifford analysis.Complex Var Elliptic Equ,2013,58(7):1037-1056
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
