基于判别分析的食品塑料包装差分拉曼光谱鉴别研究
2022-05-27王欣李春雷姜红刘峰段斌
王欣,李春雷,姜红,刘峰,段斌
(1.中国人民公安大学 侦查学院,北京 100038;2.南京简智仪器设备有限公司,北京 100020)
塑料作为一种常见的包装材料,在我国食品包装材料中的应用量已超过食品包装材料总量的50%,居各种包装材料的首位[1]。在法庭科学领域,对现场残留的食品塑料袋进行鉴别,有利于追踪嫌疑人的行为轨迹和生活习惯等。差分拉曼光谱是近年兴起的一种物证分析手段[2-6]。其采用物理和数学相结合的荧光处理方法将基线对齐相减,所得曲线仅包含差分信息[7-8],有效去除了荧光干扰,提供更为直观的化学指纹图谱。计量分析方法可将差分拉曼谱线的抽象数据转换为可分析的信息,判别分析可起到重要作用。本实验试将判别分析应用于食品塑料包装袋差分拉曼光谱的分析应用中,以期达到特征识别和种类区分的目的。
1 实验部分
1.1 材料与仪器
苏小糖牛轧糖等46个不同种类的食品塑料包装袋,样品信息见表1。
SEDRS Portable-Base便携式差分拉曼光谱仪;785 nm激光光源,光源采用双频输出,单频输出功率≤500 mW,线宽≤0.06 nm,测试波数范围250~2 800 cm-1,积分时间设置为10 s。
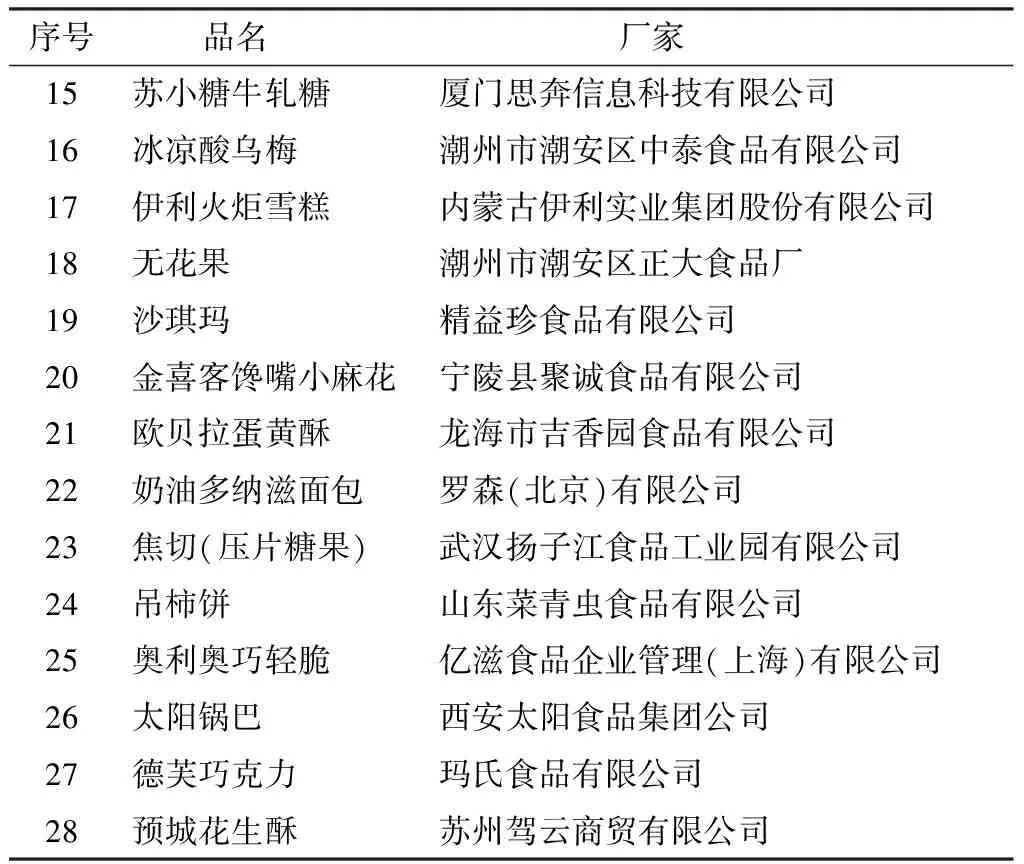
表1 46种食品塑料包装袋样品信息Table 1 Sample information of 46 kinds of food plastic packaging bags
1.2 实验方法
利用BP神经网络技术(BP)对样品的差分拉曼光谱图的基线自动进行校正,对峰面积进行归一化处理,结合差分拉曼实现解调和去背景干扰。借助因子分析对数据降维,提取特征变量以建立判别分析分类模型[9]。
2 结果与讨论
2.1 主成分分析
对46个样品的差分拉曼数据进行因子分析,所得总方差解释和成分碎石图见表2和图1。一般来说,选择所揭示的方差大于1的成分作为主成分。
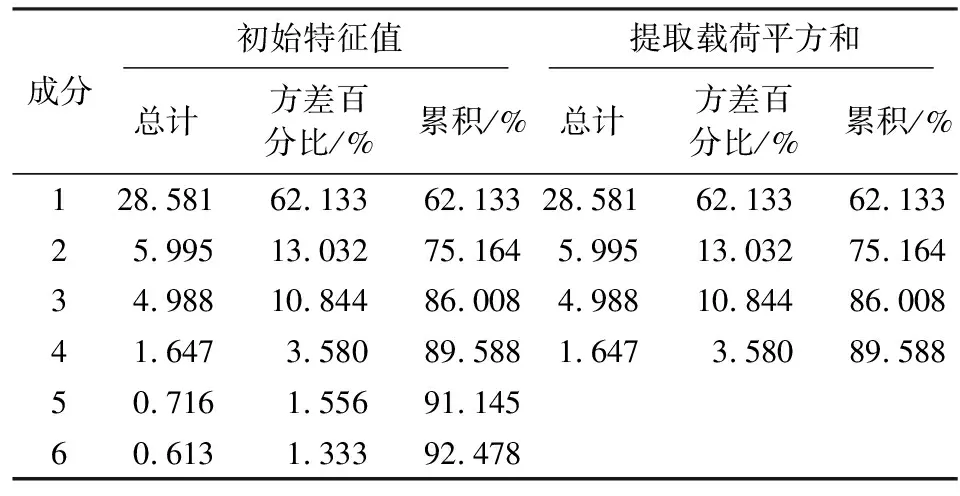
表2 总方差解释表Table 2 Explanation table of total variance

图1 成分碎石图Fig.1 Composition of gravel
由碎石图可以直观地看出,成分1、2、3、4包含了大部分信息,成分5开始就趋于平台。根据总方差解释表,前4个成分合计能够解释89.588%的方差,足以解释原始差分拉曼光谱数据信息。将前4个成分作为主成分,依此构建判别分析模型。
2.2 判别分析
针对实验收集的46个不同来源、不同厂家的样品,前期已通过系统聚类分析和Pearson相关性分析相互印证的方法将样品分为17类[10]。以各类别先验概率与各类样品量应当呈正比作为计算目的,将组内相关性矩阵进行合并,各样本的判别函数摘要见表3。

表3 判别函数摘要Table 3 Summary of discriminant function
模型构建了4个判别函数。其中,各个函数与其分组的相关性在典型相关性和特征值中体现:典型相关性和特征值的值越大,代表组内相关性越强,组间的差异就越大。Wilk’s Lambda表示组内平方和与总平方和的比值。当所有观测的组均值相等时,Wilk’s Lambda值为1;当组内变异与总变异相比小时,Wilk’s Lambda值接近于0。因此,Wilk’s Lambda值越小,贡献越大。Sig值是显著性,其值越小,说明差异越显著。由表3可知,函数1和函数2的典型相关性分别为1.000和0.991,累积方差贡献率为92.2%和96.9%,表示函数1和函数2的相关性极强,能够很好地解释样品基本特征信息。在函数检验中,函数1和函数2的Wilk’s Lambda和Sig值这一维度上均为0,表示其对模型影响的显著性极高,能够充分解释各样品的分类信息。
综上所述,以函数1和函数2为判别函数建立得到分类模型,样品的判别分析联合分布见图2,判别结果见表4。

图2 联合分布图Fig.2 Joint distribution map
由图2可知,17类样品在函数1和函数2上可以实现区分。结合表3判别分类结果,17类样品均实现了准确分类,且判别正确率达100%,依据判别分析建立的分类模型可实现对样品的有效鉴别。
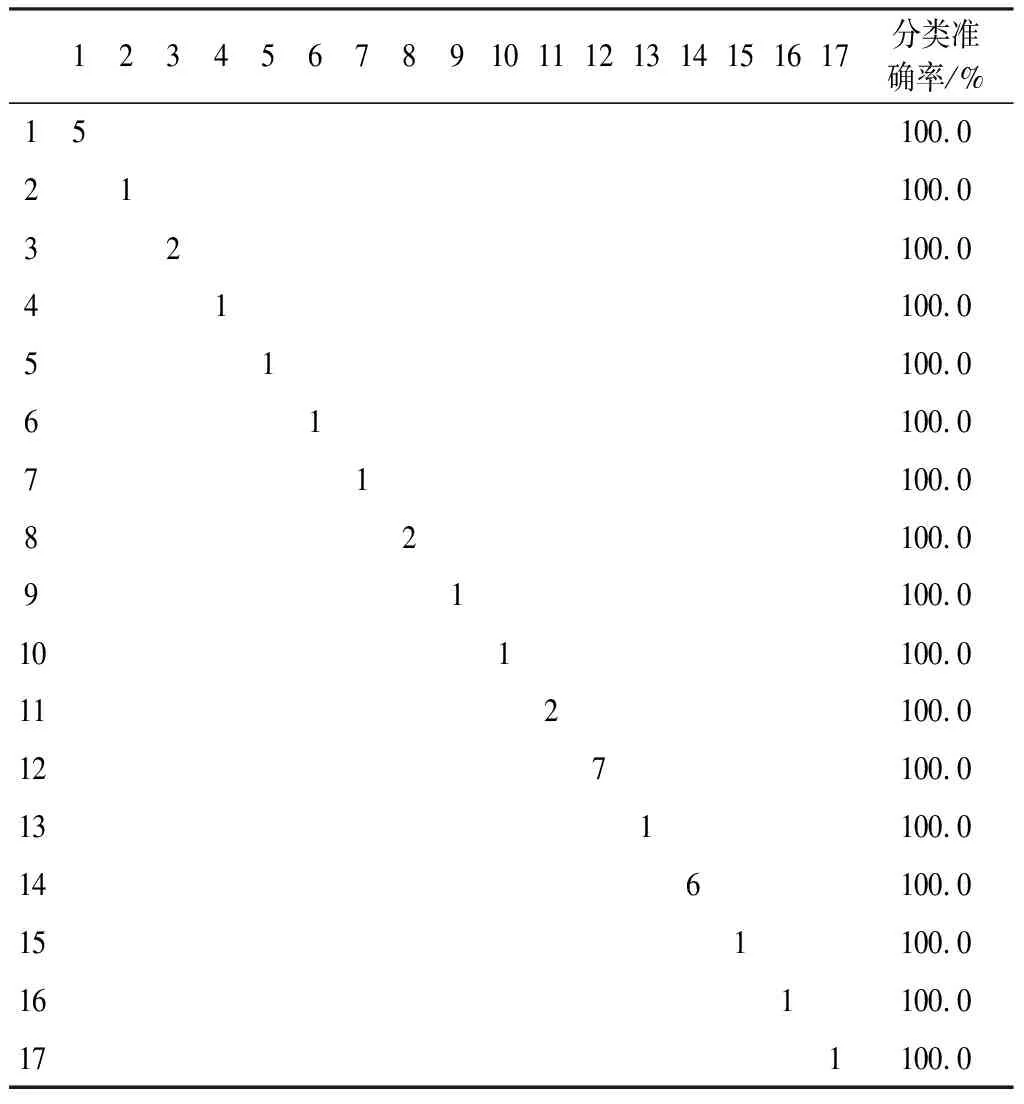
表4 17类样品的判别分类结果Table 4 Discriminant classification results of 17 types of samples
3 结论
常见的食品塑料包装袋借助判别模型对样品的差分拉曼光谱数据进行数理分析,实现了准确率达100%的鉴别分类。解决了普通拉曼光谱受基质噪声影响大和复杂成分分析繁琐的问题,该方法的建立为其他微量物证检验分析提供了新的思路,为公安机关实际办案提供了一种新的分析途径。
