基于泰勒展开的柔性加减速控制算法研究
2022-05-27王佳炜宫子阳黄泽耀范启富
王佳炜 崔 平 宫子阳 黄泽耀 范启富
(上海交通大学电子信息与电气工程学院自动化系 系统控制与信息处理教育部重点实验室)
数控技术是现代设备制造业的支柱性技术,推进数控技术的研发,对高端制造业的发展具有重要的作用,决定了制造装备的高阶性能。 高速和高精度是当前数控机床追求的两大衡量数控产品性能的重要技术指标,目前进给率最大的数控机床可以在240 m/min的条件下对复杂型面进行精确加工; 加工最高精度已经达到纳米级别。机床运动时的加减速控制是影响这两项指标的关键技术之一,直接决定了机床的生产效率和加工面质量[1]。
加减速控制算法的种类可以根据其加速度曲线的形状进行划分,直线型加减速控制算法的特性是算法计算量最小、加减速最猛烈、效率最高,因此,最先被广泛采用,但是算法在加减速阶段存在加速度突变现象, 容易导致数控机床振动,因此,仅适用于精度要求不高的加工场合[2]。为缓解加速度突变带来的振动,数控行业内陆续提出了三角型、梯型及S型等加减速控制算法,算法的加工柔性和计算复杂度与其加速度曲线的连续性正相关,较直线型加减速控制算法,能限制机床产生的部分冲击,但因未考虑加加速度曲线的连续性,在高速高精度的加工场景下,加工工件的表面光洁度不高,不适用于对加工面质量要求高的场合[3,4]。
为解决加减速控制算法其加加速度不连续导致的问题,张相胜等构造了加加速度曲线呈三角形变化的模型[5],由于模型的加加速度曲线仅C1连续, 因此不能为机床的柔性带来很大的提升。 高伟强等采用3次多项式函数确保加加速度曲线连续[6],但加加速度曲线不对称,在加减速过程的起末位置存在冲击。 李金良等对构造的连续速度曲线逐次积分[7],仅得到线性变化的加加速度曲线,系统柔性不高。
为解决上述问题, 笔者基于S型加减速控制算法,提出了一种加加速度连续的加减速控制策略,构造了连续的加加速度曲线;根据相邻加工路径间的夹角,动态调整加工路径的最大加加速度值,同时满足拐角处的降速要求;根据当前加工段长度在加工总长度的占比,对微小线段上的加减速过程进行平滑处理。 通过仿真验证整套基于S型加速减控制策略的控制性能, 证实该策略能有效减轻加工中数控机床的振动,提高加工柔性和加工效率。
1 加加速度连续方程的推导
为得到连续的加加速度曲线,直接取正弦曲线作为加加速度曲线, 正弦函数加加速度方程为:

其中,T为单个变加速阶段时间,函数在T/2处取得最大加加速度Jmax。 但正弦函数计算复杂,在算力有限的场合无法满足系统实时计算的要求。为兼顾正弦加减速的柔性和算力要求,选取低次多项式对正弦函数进行逼近,构造更适用的加加速度曲线。
考虑到计算复杂度,取sin x的二阶泰勒多项式为逼近多项式。 对正弦函数在x=π/2处进行二阶泰勒展开,为满足单个变加速阶段的起终点加加速度为零, 即在x≥0的区间内至少有两个零点,对展开后的多项式进行移位并归一化,得到的函数曲线如图1所示。

图1 正弦函数及其二阶泰勒展开多项式函数曲线
如图1所示, 处理后的多项式与sin x有较高的近似度,取其作为加加速度曲线,即:

为确保单个变加速阶段的起终点加加速度为零,即x=T和x=0时,f(x)=0,对系数进行取整,得到二阶的逼近多项式:

其中,b为待定系数,满足在区间[0,T]内f(x)≤Jmax,且在x=T/2处取得最大值Jmax,解得|b|=4Jmax。
最终得到加加速度方程如下:

该加加速度方程具有C2连续且相比正弦函数计算更简单,相比传统方法由四次多项式构造速度曲线反推加加速度曲线的方法系数更少,计算速度更快[8,9]。
2 柔性加减速控制算法构建策略
首先由加加速度方程推导得到整个加减速控制算法,其次为满足相邻加工路径夹角处的降速要求,根据夹角的大小,动态调整每段加工路径的最大加加速度值,最后为减少不必要的加减速过程引起的机床受力变化,根据当前加工段长度在加工总长度的占比,平滑微小线段上的加减速过程。
2.1 加加速度连续的加减速算法
五段式加减速控制算法其速度曲线一般由加加速、减加速、匀速、减减速和加减速5个阶段构成,根据加工路径的长度和机床运动学参数限制,可能由于无法加速至最大速度而丢失匀速阶段,只存在4个变加速阶段。
由加加速度、加速度、速度和位移之间的关系,有:

其中,a为加速度,v为速度,s为位移,ti为起始时间,μ为运动学参数方程的自变量。
与五段S型加减速控制类似, 本研究中加加速度方程j(t)如下:
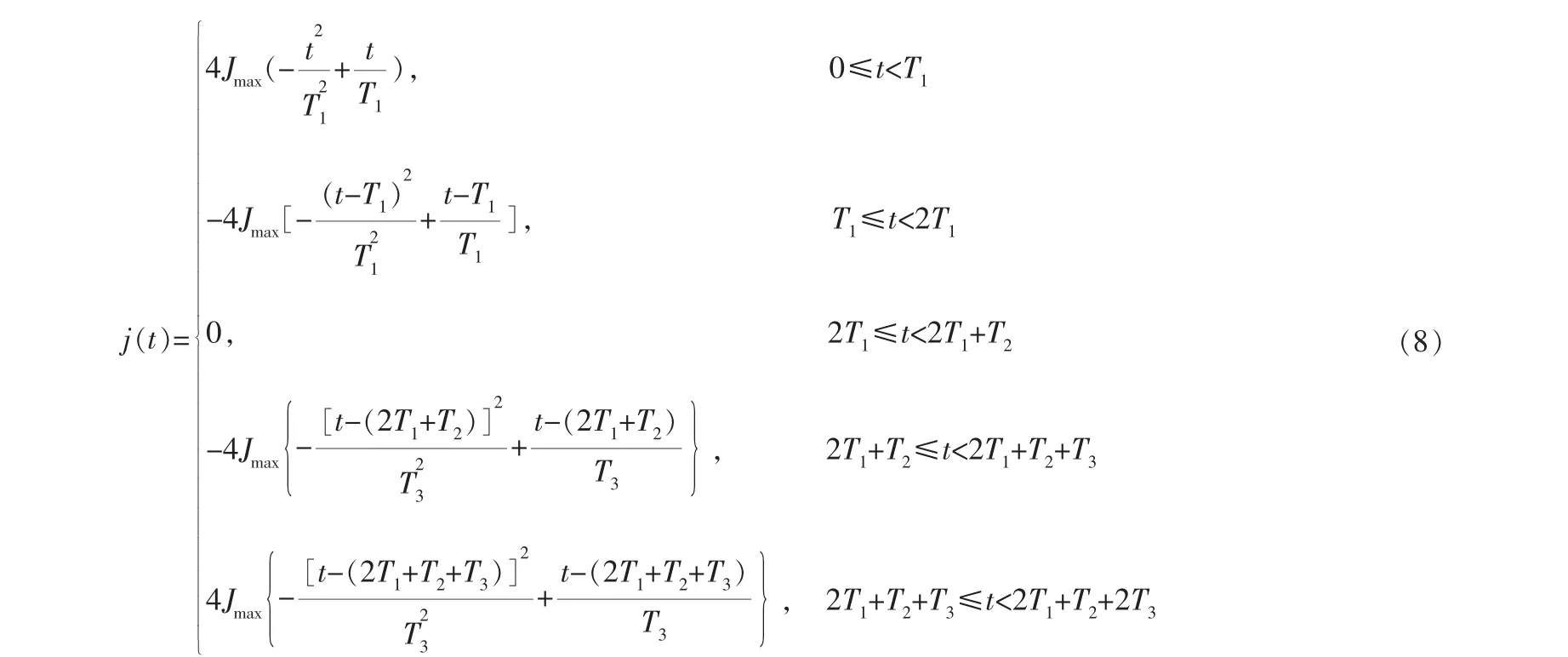
其中,T1、T2、T3分别表示一段加工路径上的加加速段时长、匀速段时长、减减速段时长。
由式(5)~(8)推出加速度、速度、位移的计算公式分别为:

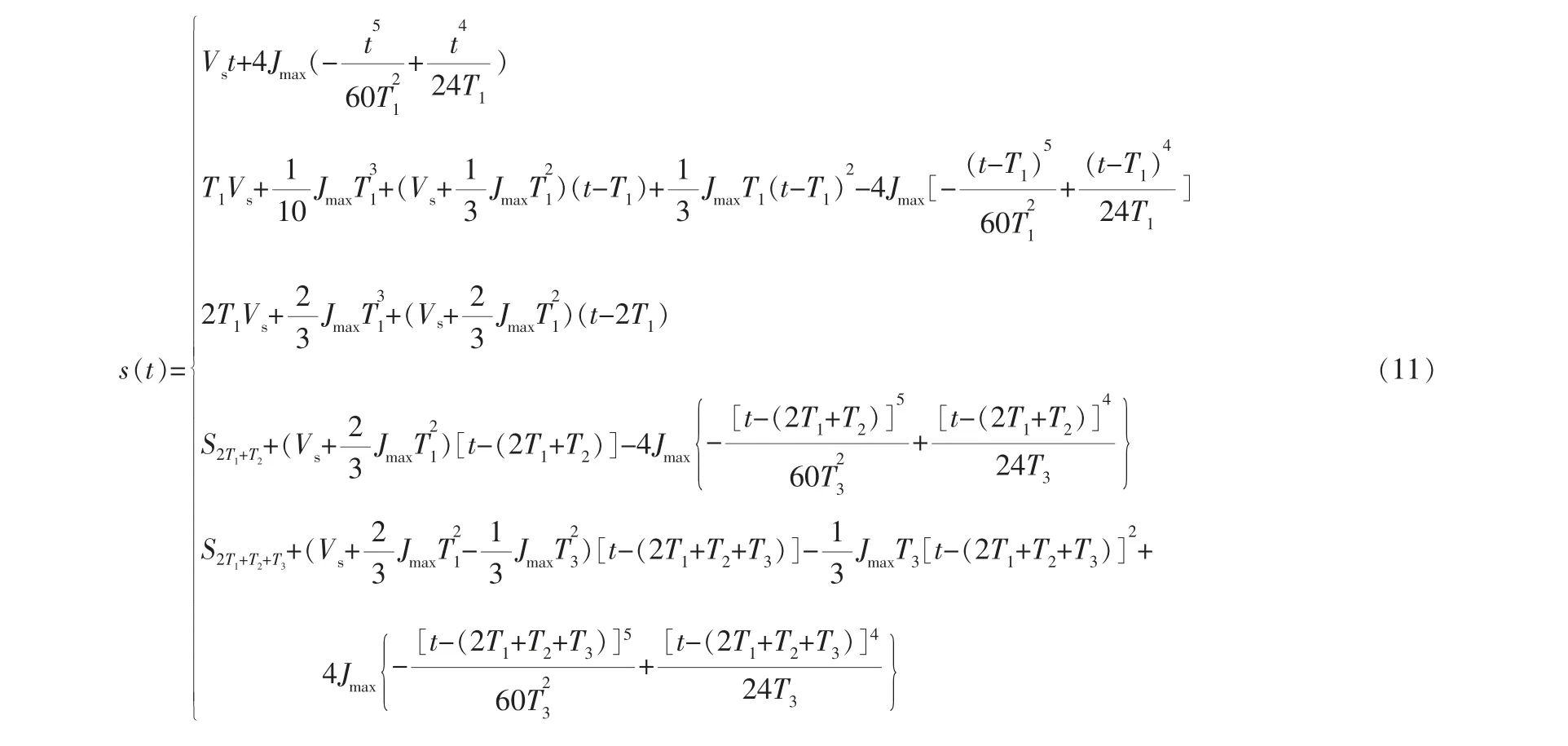

其中,Vs为初始速度。 式(9)~(11)的取值区间与式(8)相同。
2.2 动态调整加加速度最大值
传统的加减速控制算法, 其加加速度曲线是阶跃的且整个加工过程中最大加加速度值是固定的。最大加加速度决定系统加减速的柔性,若取值超出机床极限,则会产生一定冲击;取值较小,则运动的加减速过程时间延长,影响加工效率[10]。
与传统算法相比,笔者构造的加加速度连续加减速算法,由于其加加速度不是瞬间达到最大值,因此加减速过程时间更长。 为提高算法的效率,考虑在进行速度规划时,根据两段加工路径之间的夹角动态改变每一段加工路径的加加速度最大值[11,12]。
当两段加工路径之间的夹角较小时,由速度方向变化产生的机床冲击比较轻微,因此允许以较高的速度进行加工。 当夹角过大时,必须快速将速度降低以保证平稳换向,因此需要更大的加加速度以缩短减速时间,满足高速、稳定的加工要求。
唐艳丽等总结了过渡速度与夹角的关系[13],即夹角趋近于0°时,允许的过渡速度非线性地迅速增大,因此笔者将一段加工路径上加加速度最大值与其相邻路径间夹角的关系确立为:
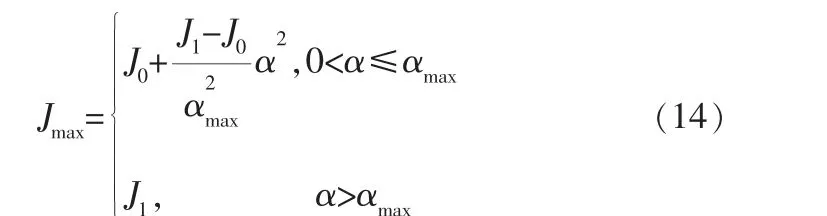
其中,α为相邻路径间的夹角;夹角最大值αmax的设定取决于系统所能承受的最大加加速度限制;J0、J1分别为系统允许的最小与最大加加速度。
单段路径上加加速度最大值与相邻路径间夹角的关系如图2所示。
当前路径上加加速度的最大值与相邻路径间夹角正相关, αmax、J0、J1根据不同的机床机械性能、加工刀路、加工工艺在进行速度规划时设定合适的值。
2.3 短线段加减速平滑
在高速、高精度的加工过程中,若加工路径出现连续微小线段,由于加工路径较短,初始速度Vs与末尾速度Ve值近似, 若均小于这段路径上系统允许的最大加工速度Vmax, 传统的加减速控制方法在微小线段上存在加速后立即减速的加减速过程,而这种连续频繁的加减速,不可避免地会对机床造成冲击,导致加工质量下降,但对于加工效率的提升很微弱,因此考虑对这类微小线段上的加减速过程进行限制。 笔者提出一种基于加工段长度的加减速平滑策略。
若S0<λS,则:

其中,S0表示当前路径长度;S表示加工路径的总长度;λ表示允许存在加减速过程的最小加工路径长度占加工路径总长度的比例;Vmax′表示当前路径上的最大速度。
对加工段上的最大速度进行限制,能保证微小线段上只存在加速或者减速过程,避免机床所受的力频繁换向,能有效减小对机床的冲击。
3 仿真示例
为验证笔者构造的加加速度曲线的连续性以及对于微小线段上加减速过程平滑的有效性,取任意8段路径,起点为(0,5),分别经过(20,5)、(35,5)、 (50,19)、 (54,19)、 (57,16)、 (61,16)、(64,19)到达终点(84,19)。 仿真轨迹如图3所示。
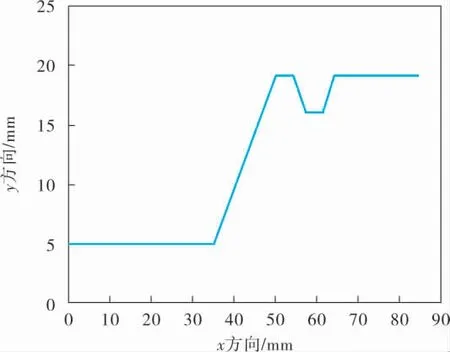
图3 仿真轨迹
运动学限制参数如下:

各段路径上的起终点速度见表1。

表1 各段路径上的起终点速度 mm/s
在插补周期为6 ms时, 通过Matlab得到整个加工路径上的仿真运动曲线如图4所示, 蓝线代表普通五段式S型加减速控制模型, 绿线代表笔者所提的加加速度连续的柔性加减速控制模型。

图4 加减速控制曲线
图4速度图上时间[0.00,1.25]区间显示第1段和第2段路径上的速度变化, 由于两段间夹角为零,因此加加速度最大值较低,无法在单段上达到最大速度,而加工时间短于传统算法,验证了2.3节中所述的可平滑部分机床运动加减速过程。 其次由图4加加速度图可以看出笔者提出的算法中加加速度曲线有良好的连续性,加减速过程更快速,平滑了在时间[1.6,2.1]区间上短线段的加减速过程,算法时间更短,速度曲线、加速度曲线更连续,证明本方法能在实现系统柔性控制的同时,提高整体的加工效率,避免小线段上频繁加减速的过程。
4 结束语
针对正弦加减速控制算法计算量大的问题,通过对正弦函数进行多项式拟合,得到了一定区间内对称且连续的加加速度方程,通过依次积分得到五段式新型加减速算法,然后根据相邻加工段之间的夹角对加工路径上的加加速度最大值进行调整,并提出微小线段上平滑加减速过程的策略。 仿真结果表明,与传统的五段式S型加减速算法相比,笔者提出的算法能同时满足高速与柔性方面的要求,提高加工效率和加工质量。
