中空扭旋元件排列方式对管内层流传热特性的影响

张傲宇,丁桂彬,王宗勇

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

近年来，随着人们环保意识的增强，提高能源利用率、节约能源越来越受人们关注.换热器作为化工生产过程中一种必不可少的设备，减小换热器体积、提高其换热效率显得尤为重要.为了达到换热器结构紧凑、换热高效的目的，可以采取的最重要方法就是增加传热系数和减小压降.传热系数的增加降低了熵产[1]；减小压降可以提高能源的利用率.在圆管中插入扭带是增强传热效果最常用的方法之一[2-5]，其主要原因是扭带使管内流体产生旋转并引起二次流，促进流体的径向混合，在离心力影响下，管中心流体和壁面边界层流体充分混合，形成一个温度比较均匀、速度变化较为明显的核心区域，同时在换热壁面附近形成一个温度和速度变化均比较显著的边界层区域，从而达到强化传热效果[6].

内置扭带的传热强化方法虽然能有效提高换热器的传热效率，但是同时也增加了流动阻力，使换热器能耗增加.Smith Eiamsa-ard等[7]对内置带中心杆的扭带、不带中心杆的扭带和规则间隔扭带3种涡流发生器进行了强化传热研究，发现各种类型扭带均可有效提高换热效率；间隔扭带在有效提升换热效率的同时也能将压降增长幅度控制在一个较小的范围内.张晓屿等[8]对内置中空扭带换热管的传热与流动特性进行了数值模拟研究，结果表明扭旋元件表面积的缩小能有效降低流体的阻力，并且能够显著提升换热管的换热综合性能.此外，张晓屿等[9]对在圆管内间隔布置多个扭旋元件时的传热和流动性能进行了数值模拟研究，研究结果表明：在充分发展的层流状态下，间隔扭旋元件可以造成圆管传热性能的强化，并且流动阻力增长不大，从而提高换热管的热-水力学综合性能.上述研究多基于元件连续排列方式，并未对元件交错排列方式做出研究.王特等[10]对内置多种错位角的交替轴扭带的管内层流换热特性进行了数值模拟研究，结果显示元件交错排列不仅可以引起漩涡流，而且在元件交错部分可以引导流体向两侧分流，引起流体扰动，促使流体更高效地混合，从而获得更好的换热效果.

郭剑等[11]对十字形扭带的传热强化效果进行了数值模拟，其研究结果表明若在受限空间的核心区添加扰流物，可使核心区的流体温度趋于均匀，若扰流物所占空间比较小，不足以产生较大的阻力，则可以实现传热强化的同时阻力增加不大，从而提高换热设备的综合传热性能.Guo等[12]分别对内置传统扭带热管与中空扭带热管的传热性能进行了数值模拟研究，结果表明与传统扭带相比，中空扭带传热性能提高了7%～20%.Li等[13]通过数值模拟研究了一种新型窄边中空扭带的强化传热特性，与传统扭带相比，该新型窄边中空扭带的最佳整体传热性能提高了28.1%.当扭带数为4、雷诺数增加到600以上时，换热管的整体换热性能最佳.

纵观现有文献可知，中空扭旋元件与传统扭带相比具有良好的综合传热性能，得到了中空扭旋元件结构包括元件宽度、扭率等对传热性能的影响规律，但关于中空扭旋元件排列方式相关研究鲜有报道，这种现状阻碍了该种类型换热器的优化设计及工业应用.因此，笔者旨在通过探究中空扭旋元件连续和交错两种排列方式对管内传热特性及流动特性的影响规律，期望为中空扭旋元件的进一步开发利用提供理论基础和技术支持.

1 物理模型及数值模拟方法

1.1 物理模型

笔者以内置中空扭旋元件换热管为研究对象，其中扭旋元件采用交错和连续两种排列方式.交错排列中空扭旋元件由4组相同的扭旋元件组成，各组扭旋元件沿换热管轴向首尾相接排布，并同心内置于管内，相邻各组扭旋元件错开90°，每组扭旋元件包含2块围绕在同一圆柱面上的扭旋片，两块扭旋片成对称布置，各扭旋片扭转角度为180°.连续排列中空扭旋元件与交错排列中空扭旋元件唯一不同之处在于相邻各组元件交错角为0°，其结构相当于将连续扭带用圆筒截去中心部分.

两种排列方式的换热管结构如图1所示.换热管结构参数为：管道内径D=20 mm；管长L=200 mm；管道入口长度Li=40 mm；元件总长Le=120 mm；扭旋板厚度δ=1 mm；扭旋元件外径do=19 mm，内径di=11 mm.

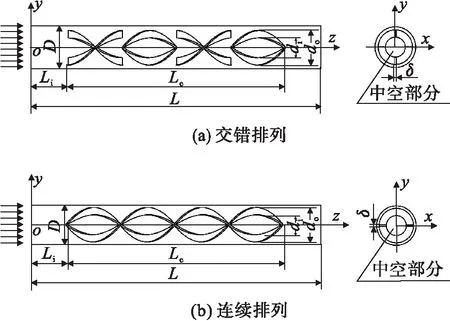
图1 内置交错和连续中空扭旋元件的换热管结构示意图

1.2 数值模拟方法

模拟过程以水为工质，为贴近实际工况，采用初始温度323 K，恒壁温边界条件(壁温为363 K)，雷诺数Re=200～1800(Re=ρuD/μ).元件与流体接触的边界采用无滑移边界条件，忽略自然对流及温度对介质性质的影响.采用Fluent 17.0进行CFD模拟，选用三维稳态模型，压力场和速度场的耦合采用Simplec算法，动量和能量方程均采用QUICK格式，连续性、动量和能量方程收敛条件均设定在10-6以下.

描述流体流动的封闭控制方程包括连续性方程、动量方程以及能量方程.

(1)

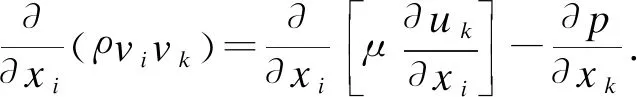
(2)

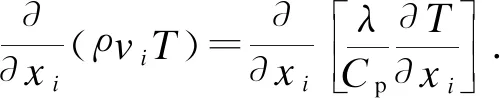
(3)

其中:ρ为密度，kg/m3；v为流体平均速度，m/s；μ为流体黏度，Pa·s;vi,vk为i，k(i，k=1,2,3)方向的速度分量,m/s;p为压强，Pa；T为流体温度，K；λ为导热系数，W/(m·K);Cp为流体比热容，J/(kg·K).

1.3 网格划分及无关性检验

笔者采用Solidworks建立几何模型，利用hypermesh进行网格划分，采用四面体网格并在靠近壁面处进行网格加密.网格质量得到提升，纵横比(aspect ratio)达5以下，雅可比值(Jacobian)达0.9以上，网格质量较好，满足模拟需要.网格局部加密如图2所示.为消除网格尺寸对计算结果的影响，对含有连续中空扭旋元件结构模型的换热管在Re=200情况下进行网格无关性检验.划分5种尺寸网格，得到每种网格数量模型下的平均努赛尔数，如图3所示.由图3可以看出：当换热管的网格数为147万左右时网格尺寸对传热系数的影响即可忽略不计.

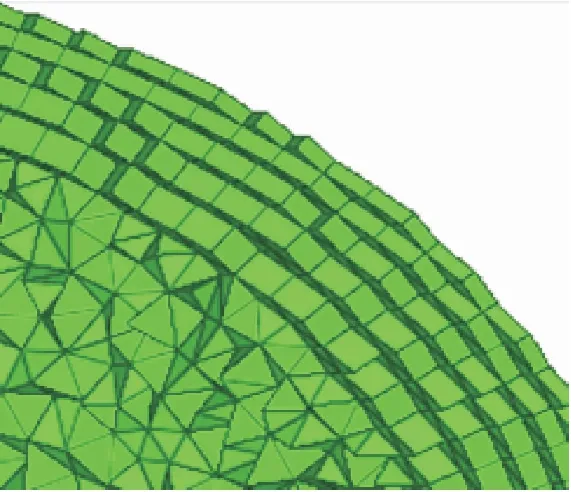
图2 边界层网格加密

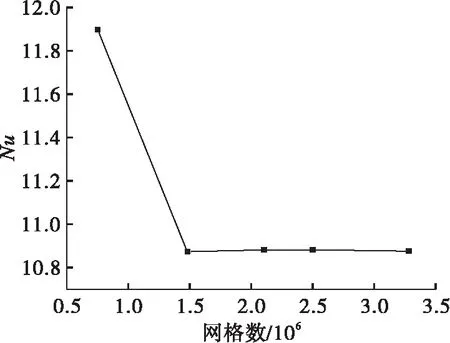
图3 换热管网格独立性验证

2 传热强化性能评价方法

2.1 综合传热性能评价因子(PEC值)

换热管的综合传热性能由传热性能和阻力性能综合体现.传热性能由努赛尔数Nu表征;阻力性能由流动阻力系数f表征，其表达式为

(4)

式中：Δp为压力降，Pa；ρ为流体密度，kg/m3；vb为流体平均速度，m/s.

综合传热性能评价因子PEC值能够考察换热器整体特性的优劣，其表达式为

PEC=(Nu/Nu0)/(f/f0)1/3.

(5)

式中:Nu0为对应光管的努塞尔数;f0为对应光管的阻力系数.

2.2 火积传热效率

Guo等[14]从导热过程与导电过程的比拟出发，提出了表征物体传热能力的新物理量火积及火积耗散的概念，火积的提出使定义一个传热过程的效率成为现实.火积耗散是物体传递热量能力的体现，热量传递是一个不可逆过程，在传递过程中部分火积将被耗散.

火积传热效率为传热性能的最直接的指标，实现强化传热的最根本原因都归结为传热效率的提升.图4表示了在恒壁温条件下换热管内流体的传热过程.整个过程的火积传热效率由下列方程求出：

(6)

式中：Q为壁面向流体传递的热量，J/s；TW为壁面温度，K；Ediss为火积耗散，J·K；Cv为定容比热容，J/(kg·K)；m为质量流量，kg/s；Tout为出口温度，K；Tin为入口温度，K.

Q=CvmTout-CvmTin.

(7)

(8)

整个过程的火积传热效率：

(9)

式中：η为火积传热效率；Ein为输入火积，J·K；Eout为输出火积，J·K.

图4 恒壁温边界条件下管内传热过程

3 数值模拟结果及分析

3.1 平均努塞尔数Nu

为了分析中空扭旋元件排列方式对传热性能的影响，笔者计算了Re=200～1800范围内共计9个雷诺数下的交错排列、连续排列元件管以及光管Nu.Nu随Re变化规律如图5所示.由图5可看出：3种结构形式换热管的Nu均随着Re的增大而增大，且两种内置扭旋元件换热管的努赛尔数明显好于光管，相对于光管传热强化效果均随着Re的增大而提高，在所分析的Re范围内连续和交错扭旋元件换热管的Nu分别为光管Nu的1.41～ 2.60倍和1.56～2.33倍.

当Re<600时，交错元件换热管的Nu高于连续元件换热管Nu.这是由于在较小的Re下，两种排列形式元件区域范围内流体的平均流速相差微小，但是交错元件换热管由于相邻各组元件存在交错结构，前一元件流出的流体会受到后一元件扭旋板的切割和分流作用，致使两元件分界面处的近壁流体特别是传热边界层内流体产生扰动，传热边界层减薄，传热系数提高；连续元件换热管内的近壁流体由于元件的连续结构，不存在流体的局部扰动，因此传热系数偏低.两种排列形式元件的努赛尔数在该Re范围相差不大，说明2块扭旋板的交错分流引起的扰流作用影响有限，若增加扭旋板数量应该能够进一步提高交错元件的传热系数.

当600≤Re≤1800时，连续元件换热管的Nu大于交错元件换热管Nu，并且两者之间的差距随着Re增大而增大.形成这种规律的原因在于：扭旋元件对流体既有旋流作用又有阻流作用，尽管交错元件能够对流体产生局部扰动而促进传热，但其对旋流的阻碍作用会随着Re增大而明显提高，导致扭旋元件区域流体旋流速度相对连续元件偏小.这种偏小程度会随着Re的增大而增大，致使连续元件的旋流强化传热作用持续增强，明显大于交错元件的旋流强化作用，而交错元件的扰流强化作用虽然随着Re增大也会有所提高，但提高幅度极为有限，进而导致连续元件的传热系数在该Re范围内要大于交错元件，且随着Re增加幅度在扩大.

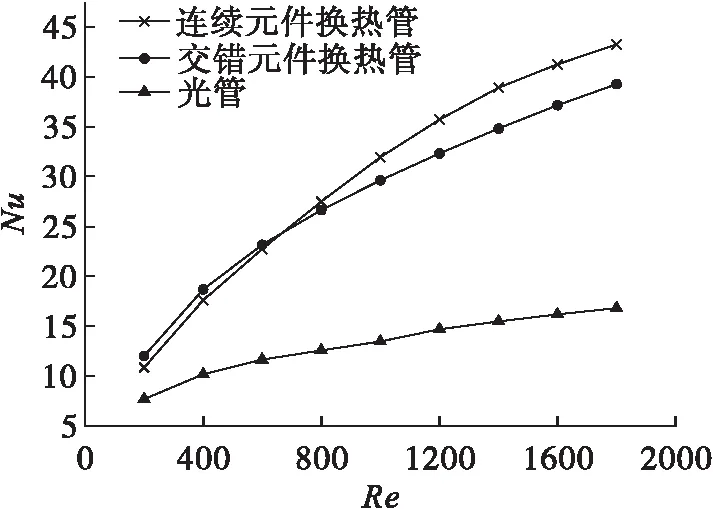
图5 传热系数Nu变化曲线

3.2 阻力系数f

如图6所示，在Re=200～1800时，连续元件换热管的阻力系数f略大于交错元件换热管的阻力系数，但两相之间相对偏差较小(<5%),特别是在Re<600范围时，两种排列形式换热管的阻力系数几乎完全相同.该Re范围内两种元件排列方式换热管的阻力系数分别为光管阻力系数的2.01～3.16倍、2.01～3.00倍.

连续元件换热管的阻力系数略高于交错元件换热管的系数阻力，从直观感觉上令人难以理解.为了便于理解这种流动现象，笔者绘制了Re=1800情况下两种排列方式换热管的横截面速度云图，如图7所示.通过计算可得连续元件和交错元件两种换热管在元件区域的平均轴向流速分别为0.88vm和0.94vm(vm为管内平均轴向流速).由此可以看出：交错元件区域范围的流速并没有因为元件交错分流的原因致使流动阻力增大、流速下降，反而比连续元件流速有所提高.形成这种状况的原因是交错元件在分流的同时，在相邻元件分界面处形成了径向涡流，该涡流对流动边界层产生了扰动，阻碍了其进一步发展变厚，从而减小流动阻力，导致整个流动区域的压力降与连续元件相比偏小，所以会形成交错元件阻力系数小于连续元件阻力系数的状况.

图6 阻力系数f变化曲线

图7 换热管截面速度云图

3.3 传热性能评价因子PEC值

传热性能评价因子PEC值能够反应传热与流体阻力的综合影响，两种内置扭旋元件换热管的PEC值变化曲线如图8所示.由图8可以看出：连续元件换热管和交错元件换热管的PEC值均随着Re的增大而增大且均大于1；在Re=1800时连续元件换热管和交错元件换热管的PEC值取得最大值，分别为1.75和1.62，证明在空心轴上插入中空扭旋元件可以取得很好的换热与流动综合性能;在Re<600时，交错元件换热管的PEC值大于连续元件换热管的PEC值,两者的偏差程度随着Re的增大而减小；当600≤Re≤1800时，交错元件换热管的PEC值小于连续元件换热管的PEC值，两者的偏差程度随着Re的增大而增大.两种排列方式换热管的PEC值随Re的变化规律与传热系数Nu变化规律基本一致，这主要是由于两种排列方式元件的摩擦系数差别不大导致的.

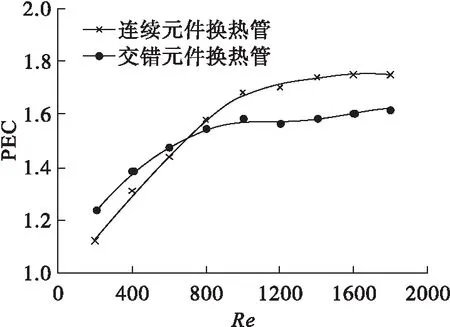
图8 PEC值变化曲线

3.4 火积传热效率η

根据火积耗散极值原理作η-Re变化曲线，结果如图9所示.

图9 火积传热效率η变化曲线

由图9可以看出：两种换热管的火积换热效率η均随着Re的增大而减小，连续元件换热管η由90.54%降至92.17%，交错元件换热管η由90.48%降至92.20%；在所分析的Re范围内，连续元件换热管的火积传热效率均高于交错元件换热管的火积传热效率，但差别不大；Re<980范围内，光管火积传热效率η高于两种扭旋元件换热管的火积传热效率，在Re>980范围内光管的火积传热效率则小于两种扭旋元件换热管的火积传热效率.由火积传热效率公式(9)可以看出，在流体入口温度及管壁温度恒定的情况下，传热效率仅取决于换热管出口温度.两种排列方式元件换热管的火积传热效率变化规律表明连续元件促进了整个管内流体的均布，促进了径向热量传递，从火积传热效率角度应优先选用连续元件结构，但从流动阻力角度考虑情况恰恰相反.

4 结 论

笔者对交错和连续排列的中空扭旋元件换热管传热性能进行了数值模拟研究，并从传热系数、综合传热性能评价因子和火积耗散极值原理3个方面对换热管的传热性能进行了评价.研究结论如下：

(1) 在Re=200～1800范围内，两种排列方式的中空扭旋元件换热管的Nu均随着Re的增大而增大，且均高于光管的Nu；在较低Re(Re<600)范围内，交错元件换热管的Nu高于连续元件换热管的Nu；在较高Re(600≤Re≤1800)范围内，连续中空扭旋元件换热管的Nu较高.

(2) 在Re=200～1800范围内，交错和连续元件排列方式换热管的阻力系数f略高于交错元件换热管的阻力系数，但两者相差不大，最大不超过5%.连续扭旋元件和交错扭旋元件的阻力系数分别为光管阻力系数的2.01～3.16倍和2.01～3.00倍.

(3) 在Re=200～1800范围内，两种排列方式元件换热管的PEC值均高于1，在Re=1800情况下，连续元件和交错元件换热管的PEC值分别取得最大值，分别为1.75和1.62，说明两种排列方式元件均能有效的提高换热管的综合传热性能.在低Re(Re<600)下，交错元件换热管的PEC值高于连续元件换热管的PEC值，证明在低Re(Re<600)下，交错元件换热管的综合传热性能优于连续元件换热管；在较高Re(600≤Re≤1800)范围，连续扭旋元件换热管的PEC值较高，证明在较高Re(600≤Re≤1800)下，连续元件换热管的综合传热性能更优.

(4) 根据火积散耗极值原理，在Re=200～1800范围内，连续扭旋元件换热管的火积传热效率η基本均略高于交错元件换热管的火积传热效率，但两种换热管的火积传热效率差别不大.