承压破碎煤体空隙率分形模型及试验研究
2022-05-27徐义洋褚廷湘冯学文代文程
徐义洋,褚廷湘,冯学文,代文程
(1. 北京中煤矿山工程有限公司,北京 100013;2. 华北科技学院 安全监管学院,河北 三河 065201;3. 中国矿业大学(北京) 机电与信息工程学院,北京 100083; 4. 安徽省皖北煤电集团临汾天煜恒昇煤业有限责任公司,山西 临汾 041204)
井工煤矿其煤自燃主要发生在采空区、破裂煤柱等地点,其中以采空区的发火次数最多、造成的损失也最严重。因此采空区自然发火的研究,一直都是矿井火灾防治领域所关注的重点方向。在煤自燃发生及发展过程中,涉及到流固介质之间的传质及传热过程,而在这一过程中,空隙率对煤自燃的发生及发展进程具有内在的作用。王继仁等应用分形理论,分析了氧气在散体煤中的扩散问题,建立了氧气在散体煤中的分形扩散方程和散体煤颗粒分形表面氧气吸附速率方程。高建良和王海生根据多孔介质渗流理论,分别模拟了采空区渗透率为均匀、分段均匀和连续性分布情况下的采空区漏风流场,发现漏风量、漏风风速分布和自燃三带的位置和宽度有很大差别。李树刚和钱鸣高通过理论分析和现场观测,分析了综放采空区垮落岩体碎胀特性与采空区流态的影响。杨永良等利用数值模拟及实测的方法,分析了煤岩垮落规律与采空区自燃规律之间的关系。自分形理论提出以来,在矿业领域此理论也得到了广泛使用。谢和平等运用分形理论研究了岩石的断裂和破碎问题,及综放工作面巷道裂隙发育情况。李宏艳等通过采动条件下裂隙场演化实验室相似模拟实验,利用分形理论定量描述了裂隙时空的演化规律。郑克洪等根据分形理论建立了煤矸破碎粒度分布的分形表达式。姜秀民等根据实验数据研究了煤粉颗粒的分形特征。KATZ等把分形几何理论用于分析多孔介质内部的孔隙结构。他们的研究表明:多孔介质的孔隙空间和孔隙界面都具有分形特征,可以用分形维数来预测多孔介质的孔隙度。以上研究可以看出不论是从宏观岩石破断、覆岩裂隙、煤矸破碎,还是在微观尺度分形理论描述空隙率也是可行的。
上述研究对描述采空区破碎煤岩空隙率提供了途径,但是由于采空区垮落的不规则性及采空区内部的不可接近性,造成对采空区自燃环境的识别比较局限。而遗煤自燃的发生却与其所在的堆积状态及环境条件息息相关,在自燃发生及发展过程中渗流场、氧浓度场、温度场之间的相互作用、相互联系,这其中最关键的问题在于采空区破碎遗煤的堆积结构的复杂性,此外进行全尺度的研究的设备手段还不能实现。因此,笔者基于煤自燃角度及采空区遗煤垮落特征,剔除矸石堆积部分,只关注垮落带内破碎遗煤承压下空隙率演变,结合分形理论,建立了颗粒煤堆积体承压下的空隙率模型,并对加载应力条件下颗粒煤的空隙率演化进行尝试。
1 空隙率对煤自燃进程影响分析
采空区遗煤自燃与覆岩垮落关系密切,煤岩垮落状态决定了采空区破碎遗煤的堆积状态,而遗煤堆积空间结构及变化,直接影响煤的蓄热环境和采空区的漏风状态及氧气分布。
1.1 覆岩垮落与堆积
据岩层的移动特征及矿压理论将煤层的上覆岩层在垂直方向上分为垮落带、裂隙带、弯曲下沉带。工作面后方的采空区,初次来压之前只有采空卸荷区,初次来压之后开始逐渐形成应力升高区和应力恢复区,但初次来压后的工作面与应力升高区之间仍存在采空卸荷区。采空区覆岩垮落与应力分布如图1所示,其中,为工作面走向卸压区宽度,为工作面走向应力集中区宽度,为采空区走向应力逐渐回复长度,m。在紧靠工作面后方,受支架及上部未完全破断的岩梁掩护,未受到基本顶来压的应力影响,浮煤及矸石处于自然堆积状态,称之为自然堆积区;随着采空区应力逐渐恢复,浮煤及矸石不再成自然状态堆积,在压应力作用下浮煤及矸石进一步破碎,密实度增加,称为破碎堆积区;当随着采空区深度的增加,采空区底板应力恢复到原岩应力水平而重新压实区,密实度最大,称为压实区。
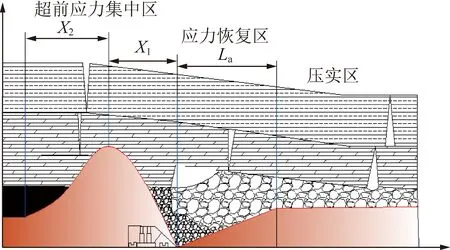
图1 采空区覆岩垮落及应力分布示意Fig.1 Diagram of the strata caving and stress distribution in goaf
采空区遗煤先后经历卸压应力区、应力恢复区及原岩应力区3个阶段,在每个阶段遗煤所承载的应力不同,致使遗煤堆积结构发生变化,进而影响遗煤堆积区域的空隙率。从煤自燃角度分析,进而影响到采空区的漏风状态、漏风强度及温度场环境,即影响采空区遗煤的自然发火的进程。文献[15]在实验室内通过对散体煤进行加载实验,得到了轴向应力与碎胀系数的关系,发现随着轴向应力增加,碎胀系数降低,逐渐趋于压实,进而改变破碎煤体的空隙率。所以如何确定采空区承压破碎煤体在应力变化条件下的空隙率响应特征,对研究采空区煤自燃的发生显得尤为重要。
采空区覆岩应力对空隙率的影响是间接的,是通过影响采空区煤岩的碎胀系数来影响空隙率的,空隙率与碎胀系数存在以下关系:
=1-1
(1)
由式(1)可以看出,空隙率与碎胀系数成正比关系:碎胀系数越大,空隙率亦越大。
1.2 空隙率与煤自燃关系
对于一个特定的综放工作面,其通风方式、供风量、风压分布等基本确定,影响漏风强度的主要因素是松散煤体的空隙率。漏风强度是风压梯度、空隙率的函数。
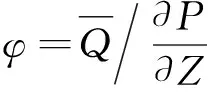
(2)
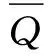
由式(2)可以看出,当漏风通道两端压差一定情况下,空隙率越大,漏风量越大,空隙率影响漏风区域的漏风强度。在采空区漏风强度一定的情况下,采空区遗煤堆积环境的氧气体积分数的分布与空隙率分布有关。
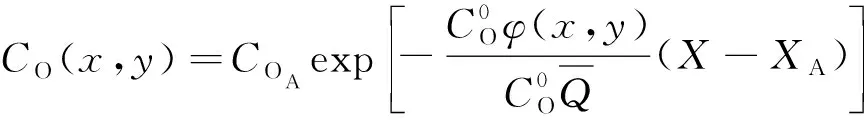
(3)
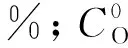
由式(3)可以看出,采空区某点的氧气体积分数与空隙率的分布有关。
根据能量守恒定律,考虑气固两相时,采空区遗煤的温度方程为
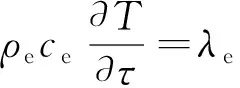
(4)
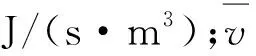
由式(4)可以看出,采空区遗煤堆积空间的空隙率对温度场的演化具有重要影响。
综上,可见空隙率对采空区漏风强度、氧气体积分数的分布、温度场的分布影响较大,因此基于采空区应力恢复特征,如何定量描述其在应力扰动下的空隙率计算模型,对煤自燃研究来说具有一定的意义。
2 承压破碎遗煤的分型模型
采空区遗煤堆积空间四周受力,轴向覆岩应力作用为主动应力,同时由于遗煤散体的变形、滑动受两侧煤壁、老开切眼及支架的束缚限制,宏观表现为以轴向压实为主,四周相对位移固定的受力状态。在承压破碎散体渗透性方面刘卫群、李顺才等研究了不同破碎程度下压实的渗透系数变化规律,指出破碎岩石的渗透性不仅和外载水平及初始孔隙度有关,还与碎石的粒径、颗粒的排列方式以等有关。PAPPAS和MARK通过20组单轴压缩实验,详细研究了采空区垮落材料的力学性质,通过应力-应变关系,获得了有关岩石的力学参数及散体破断特征。梁军等采用大型压缩仪进行了堆石蠕变试验和颗粒破碎测试,指出堆石破碎有主压缩破碎和蠕变破碎2类,其中蠕变破碎是堆石料骨架应力的重新分布导致粗大颗粒棱角或者软弱颗粒发生破碎、细化,颗粒排列进一步调整,如图2所示。
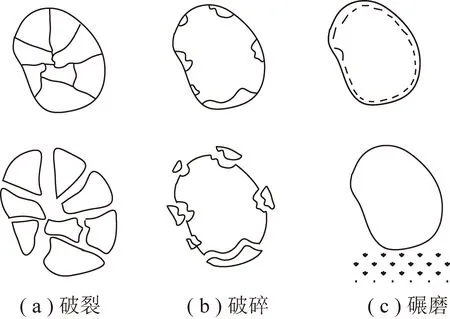
图2 颗粒破碎类型Fig.2 Particle breakage types
采空区遗煤依次经历应力三区时,会再次发生破碎,遗煤颗粒破碎在覆岩荷载作用下产生结构的破裂或破损,进而影响其堆积结构与状态。
2.1 遗煤堆积空隙率分形模型
TYLER等提出了质量和孔径关系的标准化方程,且通过假设不同土壤粒级具有相同密度的条件,建立了土壤粒径分布分形维数的质量分布模型。由于采空区遗煤粒径、形状不一,根据TYLER的研究结果,可以通过不同直径的筛子筛分试样,通过筛下试样的质量和总试样的质量建立函数关系,分析遗煤粒度的分布。
设()为筛下试样质量,()为筛上试样质量,为试样总质量,定义关联函数()为
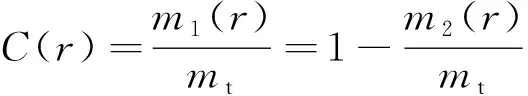
(5)
在三维空间中,大于某一粒度的粗粒颗粒所构成的体积为,则有
=[1-()3-]
(6)
式中,为破碎分形维数;,均为常数,与遗煤颗粒的大小、形状有关。
假定遗煤颗粒具有相同的密度,则大于某一粒径的遗煤质量为
()=[1-()3-]
(7)
若令=0,可得到试样的总质量;若令等于试样中的最大粒径,则有()=0,代入式(7)可得=,则可得到遗煤颗粒质量与粒径之间的分形关系:

(8)
对式(8)两边取对数,则有
ln[()]=(3-)ln()
(9)
通过物理筛分、称重统计,可得到()的统计值,并依据线性回归求得直线部分的斜率,即(3-),进而得到遗煤破碎分形维数。
采空区垮落遗煤空隙率为破碎遗煤间的空隙体积与整个垮落堆积体体积之比,设垮落遗煤的颗粒尺寸为,根据密度定义,则有
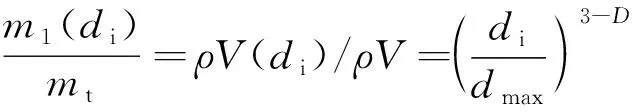
(10)
其中,()为颗粒特征尺寸小于的遗煤分形体积,m;为垮落岩体总体积,m,为破碎煤体密度,kg/m。则对于粒径小于部分遗煤堆积体积为
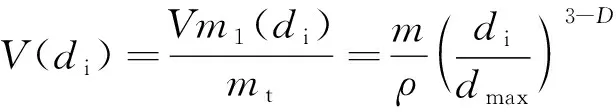
(11)
则,粒径处于区间(,+d)内的堆积体积为
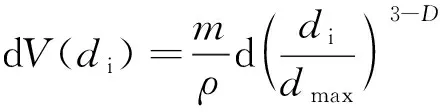
(12)
则,垮落遗煤的分形总体积为
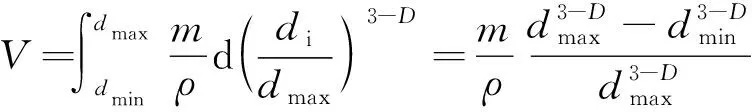
(13)
则有
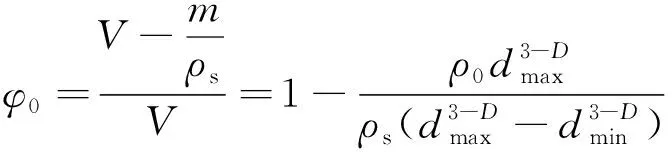
(14)
式中,为垮落遗煤自然碎胀空隙率;,分别为最小及最大颗粒粒径;为煤的质量;为自然碎胀遗煤密度;为煤层的密度。
2.2 承压破碎煤体空隙率演变模型
采空区遗煤堆以轴向覆岩应力作用为主动应力,同时由于遗煤散体的变形、滑动受两侧煤壁、开切眼及支架的束缚限制,宏观表现为以轴向压实为主,因此可以通过侧限压实实验,辅助应力-应变关系,得到承压破碎遗煤的视密度与真密度之间的关系。
轴向应变为
=Δ
(15)
式中,Δ为压缩变形的煤体高度;为压缩变形后煤体高度。
假设在侧限压实实验过程中完整煤样初始质量为,初始碎胀密度为,自然碎胀堆积装置内煤样高度为;承载破碎煤体的密度为,承压过程中应变为。则承压后煤样在不同应力状态下的高度=(1-),破碎煤体承压过程中,不断被压实,空隙体积随压实程度不断减小,由质量守恒得
=1(1-)
(16)
根据空隙率定义,则承压破碎煤体的空隙率,可表达为
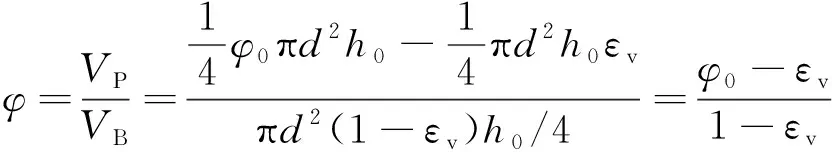
(17)
式中,为颗粒堆积体的空隙体积,m;为颗粒堆积体表观体积,m。
式(17)有效使用,需满足:≤,理论上,数值上当=时,煤样完全被压实,无任何空隙。
在压实过程中应力-应变的关系可表达为
=e
(18)
式中,为轴向压应力;,为压实回归系数。
承压破碎遗煤的空隙率分型模型为
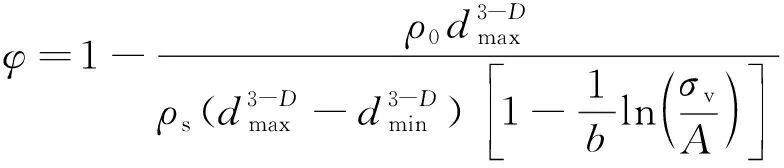
(19)
3 承压破碎煤体空隙率实验
3.1 实验煤样及方法
所选煤样来自山西恒昇煤业9106工作面,在该工作面倾向支架后部3个不同位置取样,选取15 mm以下粒径的混合煤样作为试验煤样,经自然风干后,进行筛分,确定了自然碎胀区遗煤15 mm以下遗煤堆积体的级配的构成,见表1,其中为颗粒粒径。
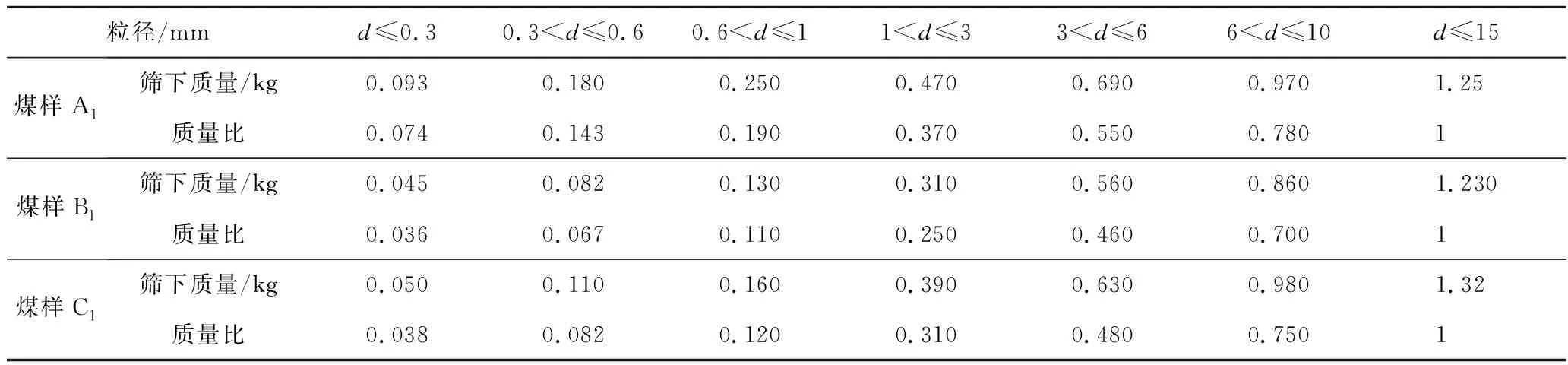
表1 初始各粒径组质量
其中相同位置煤样各准备2份分别标记为A,B,C,A,B,C,保持级配相同,一份用于应力应变测试,一份用于特定轴向加载应力下的分形维数确定。
利用实验室内自主设计的承压破碎遗煤渗透率演化及自燃测试装置,如图3所示。通过此装置,可对采空区筛选的煤样开展轴向加载实验,通过设定不同的轴向加载强度,通过重新筛分,可确定加载后煤样的级配构成及承压破碎煤样的空隙率。

图3 承压破碎煤体空隙率测试实验装置Fig.3 Porosity test device of the compacted broken coal
3.2 原始煤样分形维数确定
结合表1,对煤样粒径与对应筛下质量比,通过对数取值,然后线性回归,根据拟合曲线斜率,通过式(9)可回归得到原始煤样的破碎分形维数,如图4所示,其中,为粒径以下的煤样质量。通过对原始煤样的级配筛分及分形维数回归,利用空隙率分形模型式(14),得到了自然堆积状态下的A,B,C煤样的空隙率(表2)。发现利用分形模型计算得到的空隙率与空隙率定义计算出的空隙率误差在0.045~0.086,空隙率分形模型可用于采空区遗煤孔隙率计算。
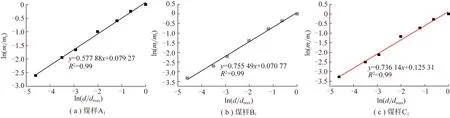
图4 原始煤样ln(di/dmax)与ln(mi/mt)回归Fig.4 Regression curves of the initial coal sample between ln(di/dmax)andln(mi/mt)

表2 原始煤样分形维数与空隙率
3.3 承压破碎煤体的分形维数
分别对煤样A,B,C进行了承压实验,通过回归分析确定了3个煤样的应力-应变关系,见表3。
由表3可知破碎煤体应力-应变符合指数关系。随着应力增加,破碎煤样的应变逐渐增加,即煤样逐渐被压实,结合图1可知在采空区横三区内,随着采空区应力逐渐恢复,采空区遗煤堆积体逐渐被压实。

表3 煤样承压应力应变拟合关系
对不同加载应力状态下的破碎煤样再次筛分,通过分形理论可得到破碎煤样的承压破碎分形维数。
分别测试了煤样A,B,C在加载8,12及15 MPa后煤样承载破碎后的级配情况,并对其回归,得到加载后A,B,C的破碎分形维数,如图5所示。发现承压破碎煤体分形维数增大则说明受载煤样更加破碎,在应力加载状态下其空隙率逐渐减小。
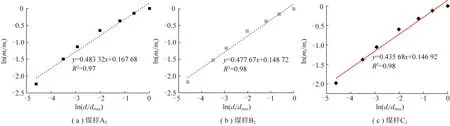
图5 承压破碎后煤样ln(di/dmax)与ln(mi/mt)回归Fig.5 Regression curves after compacted between ln(di/dmax)andln(mi/mt)
3.4 模型与实验结果对比
通过对煤样A,B,C的轴向加载实验,根据其煤样质量、煤样真密度、压实位移,可得到不同应力状态下的实验空隙率;通过表2,4的实验数据,根据式(19),可确定其分形理论空隙率,见表5。
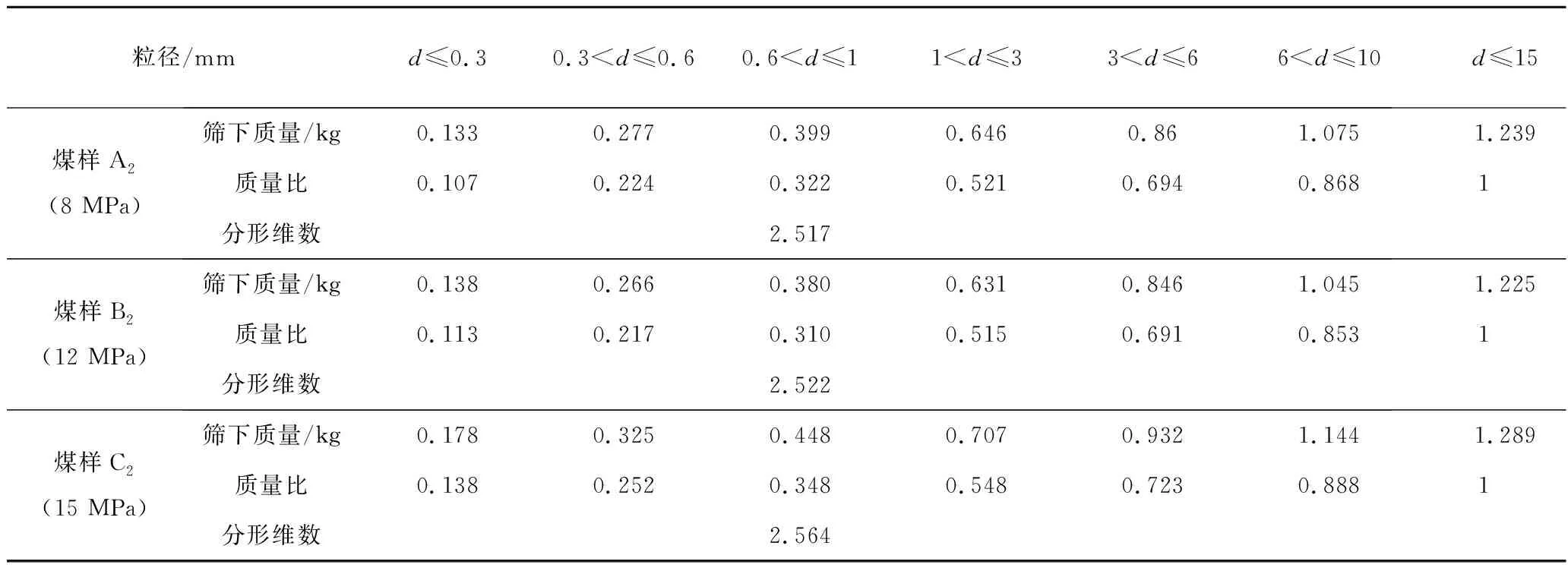
表4 轴向加载后级配及分形维数

表5 承压煤样分形空隙率计算结果
经实验测试及理论计算,得到了煤样A,B,C分别在加载8,12,15 MPa下的空隙率,通过2者比较,3个煤样的误差分别为0.106,0.028,0.062,说明通过承压破碎遗煤的空隙率分形模型是可以用于预测不同应力状态下的空隙率变化。
3.5 承压破碎煤体空隙率预测方法
以B煤样的应力应变曲线为例,结合承压破碎遗煤空隙率分形模型,可对不同应力状态下的破碎煤体空隙率演化进行预测,(式(20))。
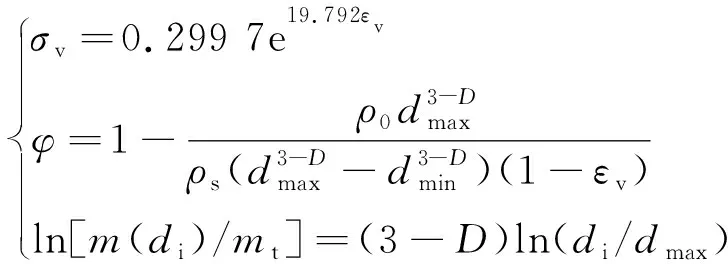
(20)
承压破碎煤体空隙率预测方法可简述为:首先获得其应力-应变曲线,然后根据煤样的级配构成确定其破碎分形维数后,根据所建立的承压破碎煤体空隙率分形模型可对其预测。
4 结 论
(1)以空隙率对煤自燃影响为切入点,分析了采空区空隙率对煤自燃发生中的漏风强度、氧气体积分数分布、蓄热环境的影响,明确了空隙率变化对采空区煤自燃的影响作用。
(2)结合采空区应力恢复及承压破碎煤体压实特征,通过引入分形理论,建立了承压破碎煤体空隙率分形模型。
(3)通过承压破碎煤体压实实验,明确了压实前后分形维数的变化,基于实验数据与推到模型进行了验证,实验结果与理论计算结果误差不大,所建立的模型具有一定的可靠性。通过该研究,为后续研究恒昇煤业采空区漏风、煤自燃氧化区域及瓦斯运移提供了理论指导。
(4)因受限于采空区破碎煤岩全尺度样本索取困难,本文仅以小样本尺度煤样为对象进行了研究,这对于研究采空应力恢复状态下的空隙率演化提供了一种新思路。
