改进海鸥优化算法在光伏系统MPPT中的应用

李大华，聂 前，田 禾，付文成，杜 洋

(1.天津理工大学电气电子工程学院，天津 300384；2.天津市复杂系统控制理论及应用重点实验室，天津 300384；3.天津市三源电力智能科技有限公司，天津 300409)

近年来，由于传统的化石能源储量不断减少以及造成的环境问题日益严重，太阳能因绿色无污染的特点得到了广泛的应用[1]。光伏阵列处于均匀光照条件下，光伏输出功率(P)对光伏电压(U)的曲线仅包含一个峰值点。这一点可以简单地使用任何传统的跟踪方法来捕捉，如电导增量法和扰动观察法[2]。然而在实际应用中，光伏阵列会因环境的影响(树木、房屋等遮挡)造成每块光伏板的光照强度不同，导致P-U曲线中出现多个峰值点，其中包括全局最大功率点(global maximum power point，GMPP)以及局部最大功率点。传统的跟踪方法易受局部最大功率点的影响而陷入局部最优，无法捕捉到全局最大功率点，从而导致跟踪失败。

为了解决局部阴影情况下传统最大功率点跟踪(MPPT)控制方法无法搜索到GMPP 的问题，国内外许多学者展开了大量的相关研究。文献[3]提出将粒子初始位置分散定位在可能的峰值点电压处，虽然可以跟踪成功，但是算法迭代次数过多导致速度下降明显；文献[4]提出自适应细菌觅食优化算法跟踪最大功率点，根据细菌觅食程度自适应在线调整移动步长与驱散概率，具有跟踪速度快的优点，缺点是参数设置过多，且易发生过早收敛；文献[5]利用布谷鸟算法的全局搜索能力与扰动观察法的局部细致搜索能力相结合，可以提升跟踪的速度与精度；文献[6]提出简化的蚁群优化算法实现最大功率跟踪，通过不断迭代使占空比更新，实验结果表明其大大提升了追踪速度。

海鸥优化算法(seagull optimization algorithm，SOA)是由Dhiman 和Kumar 在2019 年提出的一种新的基于生物行为启发的元启发式算法，相对于其他智能优化算法，该算法原理简单，参数设置简单，并且在收敛速度方面也具有一定优势，在很多工业领域都得到了实际的应用[7]。但SOA 和很多优化算法一样，存在易陷入局部收敛的问题，尤其遇到复杂多峰值的问题时。本文在海鸥优化算法的基础上引入混沌序列[8]，增加种群位置的多样性，以此来克服过早收敛的问题，加强算法在全局搜索与跳出局部搜索的能力。传统的SOA算法搜索过程为线性，而光伏输出P-U 特性曲线为非线性，为此提出改进海鸥优化算法(I-SOA)，将非线性搜索控制应用到MPPT 中，来提高算法的速度和精度。

1 光伏电池等效电路及输出特性

通常将光伏电池的工作状态用一个等效电路来进行模拟，如图1 所示。

图1 单个太阳电池等效电路图

由图1 可知光伏电池的电气特性为：

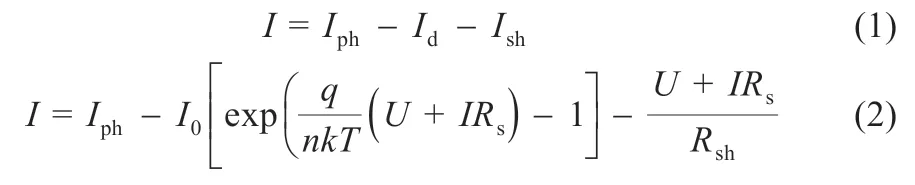
式中：Iph为光伏电池的光生电流；Id为暗电流；I0为二极管的反向饱和电流；Rsh为等效并联电阻；Rs为串联等效电阻；n为二极管特性因子；k为波尔兹曼常数，1.38×10-23J/K；T为光伏电池温度；q为电子电荷；I为光伏电池的输出电流；U为光伏电池的输出电压。

由于单体的光伏电池输出电压很小，无法满足日常生活的应用，所以通常将几个光伏电池通过串并联的方式封装成光伏组件[9]。串联要求所有模块产生相同的电流，在部分阴影条件下，阴影模块无法产生与非阴影模块相同的电流；此时，阴影模块将消耗而不是提供电流，导致光伏组件局部温度过高，形成热斑现象。为了防止热斑现象，旁路二极管通过模块并联使用，以简单地绕过阴影模块，这导致在P-U 和IU 曲线上出现多个峰值[10]。

本文在Simulink 平台上建立了3×1 的光伏阵列仿真模型，如图2 所示，主要利用该仿真模型对光伏阵列处于局部阴影情况下的输出特性进行研究分析。其中光伏电池的参数为：开路电压均为36.3 V，短路电流均为7.84 A，最大功率均为213.15 W，最大功率点电压均为29 V，最大功率点电流均为7.35 A。在标准环境温度(25 ℃)下设置三种情况，见表1。将光伏阵列置于此情况下进行仿真，得到光伏输出曲线如图3 所示。

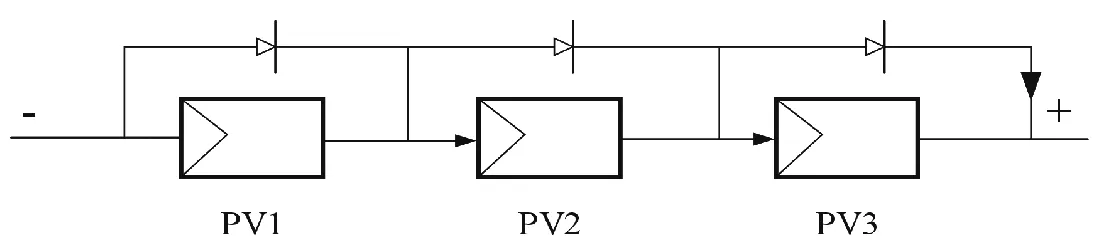
图2 光伏阵列拓扑结构

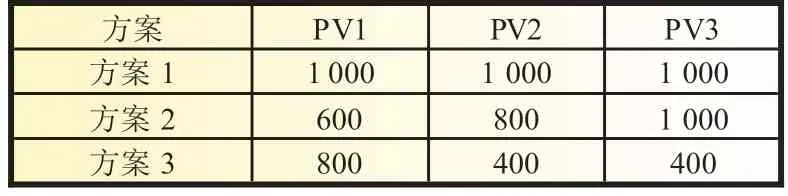
表1 不同环境下光伏组件所受的光照强度 W/m2

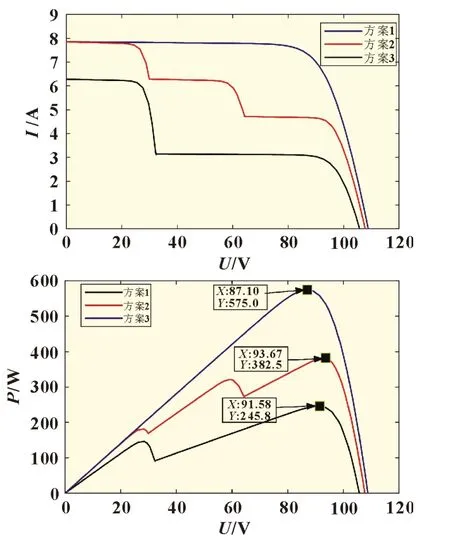
图3 遮阴下光伏阵列I-U和P-U输出曲线

由图3 可知，当光伏阵列处于方案1 时，在光照均匀条件下光伏阵列的输出功率曲线呈单峰；当光伏阵列处于方案2时，输出功率曲线有三个峰值；而当光伏阵列处于方案3 时，输出功率曲线有两个峰值。由此可得，光伏阵列处于局部阴影的情况下，其P-U 特性曲线具有多个峰值点，为了提高输出功率，引入一种能快速、准确跟踪到全局最大功率点的智能算法显得尤为重要。

2 海鸥优化算法简介

2.1 海鸥优化算法

海鸥优化算法是一种新的基于生物行为启发的元启发式算法，其思想源于自然界中海鸥的迁徙和攻击行为[11]。

2.1.1 迁徙(全局搜索)

算法通过模拟海鸥种群的迁徙来实现全局搜索。此阶段海鸥应满足3 个条件。

(1)避免碰撞：为了避免海鸥之间互相碰撞，算法采用附加变量A计算海鸥的新位置。

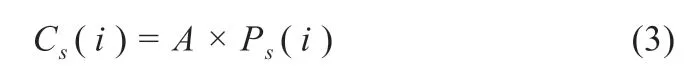
式中：Cs(i)为不与其他海鸥发生碰撞的新位置；Ps(i)为海鸥当前位置；i为当前迭代；A为海鸥在给定搜索空间中移动行为的参数。

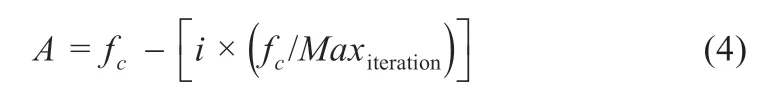
式中：fc可以控制变量A的频率，将A的值从2 线性下降到0；Maxiteration为迭代总次数。

(2)最佳位置方向：海鸥之间避免碰撞后，海鸥个体会向最佳位置所在方向移动。

式中：Ms(i)为最佳位置的方向；B为随机数，作用是平衡全局和局部搜索。

式中：rd为[0,1]范围内的随机数。

(3)靠近最佳位置：海鸥移动到不与其他海鸥相撞的位置后，就向着最佳位置的所在方向进行移动，到达新的位置Ds(i)。

2.1.2 攻击(局部搜索)

海鸥找到猎物后，会不断改变攻击的角度和速度，以螺旋运动的方式攻击目标。x、y和z平面中的运动行为描述如下：

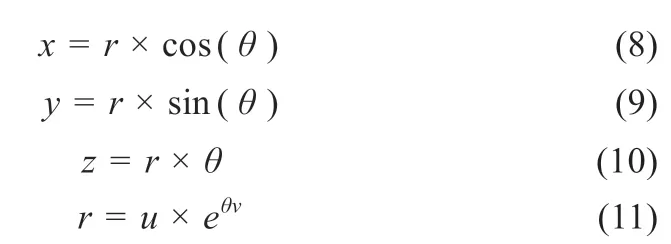
式中：r为每个螺旋的运动半径；θ为[0,2π]范围内的随机角度值；u和v为螺旋形状的相关常数。海鸥的攻击位置由公式(8)～(11)计算得到。

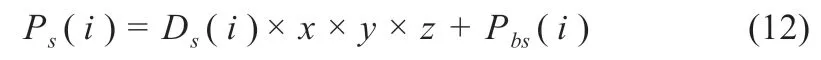
式中：Ps(i)为海鸥的攻击位置(保存最优解决方案并更新其他搜索代理位置)。

2.2 改进海鸥优化算法的附加控制因子

海鸥优化算法与传统的智能算法粒子群相比，具有易于实现、收敛速度快、参数调整简单的优点。然而，SOA 的全局优化搜索过程是线性的，如式(4)所示。这种线性搜索方式意味着不能充分利用SOA 的全局搜索能力。因此，本文提出一个非线性搜索控制公式，如公式(13)所示，可以针对海鸥群探索过程阶段，提高算法的速度和精度。

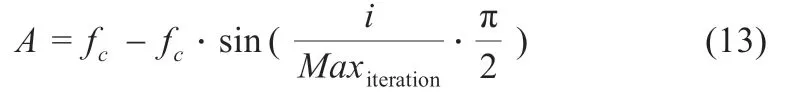
该方法中的A值在递减过程中呈现出非线性趋势，可以更好地提高全局搜索能力，每次迭代都能避免海鸥之间的位置冲突，也能更好地平衡探索与开发。

如图4 所示，与原SOA 算法相比，在迭代初期，非线性控制因子A前期骤减可增强算法的全局搜索能力及保持种群的多样性；在迭代后期，A缓慢递减可增强局部搜索能力。这样既可以保证在最大功率跟踪过程中不易陷入局部最优，又可以缩短整个寻优过程的时间并提高寻优精度。

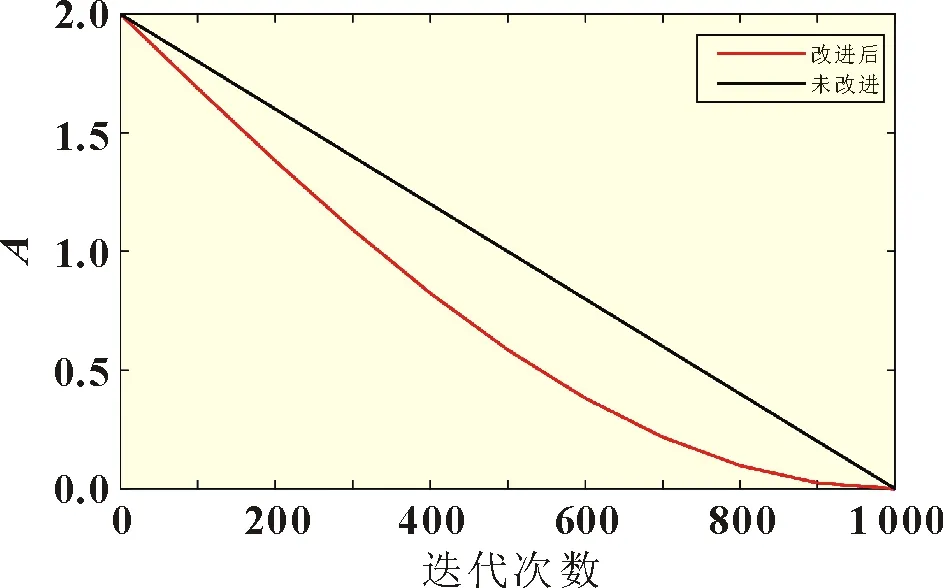
图4 控制因子A随迭代次数的变化趋势

2.3 混沌优化理论

SOA 算法随机确定海鸥的初始位置，如果随机产生的初始值是不利的，随着迭代次数的增加，海鸥种群的多样性会下降，导致算法提前收敛，陷入局部最优。为了解决此问题，本文引入混沌优化。混沌映射是一个完整的初始种群，可以确保初始种群始终进行无序随机运动。混沌变量在一定范围内具有随机性、遍历性和规律性的特点，与SOA 算法相结合可以丰富海鸥种群多样性，从而避免陷入局部最优[12]。选择广泛使用的logistic 映射作为混沌模型，以提高种群的初值。模型如下所示：

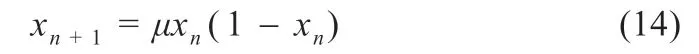
式中：μ为控制变量，值越大表示混乱程度越高，取值在[0,4]；xn取值在[0,1]之间。

3 改进海鸥优化算法在MPPT 中的应用

海鸥的位置代表光伏电池的输出电压，适应度值为光伏电池的输出功率，具体迭代步骤如下。

步骤1：初始化种群规模，最大迭代次数t=1 000，fc的初始值设为2，rd在[0,1]内随机选取，θ是[0,2π]范围内的随机角度值。u和v的值设为1，混沌控制变量μ设为4。

步骤2：使用计算适应度函数Ps(i)计算每只海鸥的适应度值。

步骤3：根据式(13)利用改进后的非线性公式计算新的附加变量A的值。

步骤4：根据式(7)计算新的海鸥位置，用式(8)～(12)计算海鸥攻击新位置Ps(i)，并检查更新后的位置是否越界。

步骤5：得到海鸥更新的位置，再次计算更新后的海鸥个体位置适应度值，通过比较再次更新位置和最优适应度值。

步骤6：判断算法执行是否运行至最大迭代次数，若运行到达则输出最佳海鸥位置(Ubest)和适应值(Pbest)，且算法结束；若不满足，则跳转到步骤3 继续搜索。

相关的流程如图5 所示。

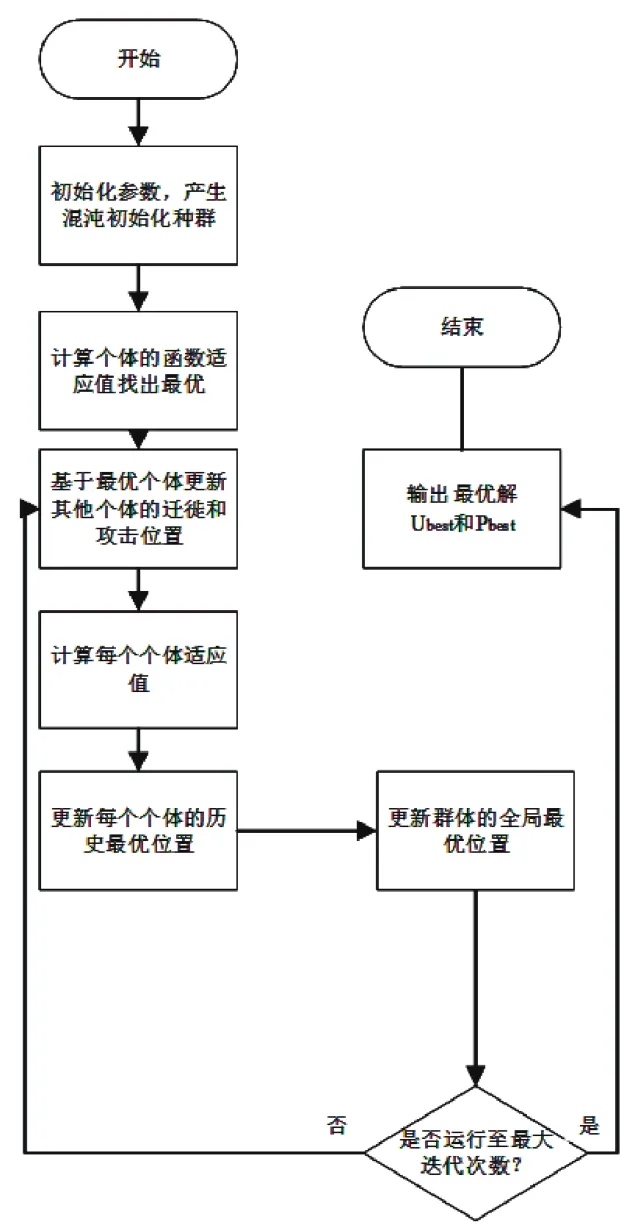
图5 改进海鸥优化算法在MPPT中的应用

4 仿真实验

为了验证I-SOA 算法在光伏MPPT 系统中的有效性，在Matlab/Simulink 中搭建了由三个光伏组件串联构成的光伏阵列模块、I-SOA 算法的MPPT 控制模块、Boost 变换器模块以及PWM 驱动模块。如图6 所示，Boost 电路的参数设置为：C1=50µF，C2=100µF，L=5 mH，R=150 Ω。

图6 MPPT控制系统仿真模型

4.1 静态环境下的仿真分析

静态条件下的仿真中，仿真温度设置为标准温度25 ℃，PV1 为1 000 W/m2，PV2 为800 W/m2，PV3 为600 W/m2。此时理论最大输出功率为382.5 W(由图3 知)。图7 为I-SOA 算法、SOA 算法及PSO 算法在静态阴影条件下的仿真效果对比图。表2 给出了这三种控制方法的各项对比。其中I-SOA 算法在0.178 4 s 追踪到了最大功率382.3 W，与理论值382.5 W仅差0.2 W，追踪效率为99.95%，相比于另外两种控制方法，在收敛时间以及追踪效率上都有提升。

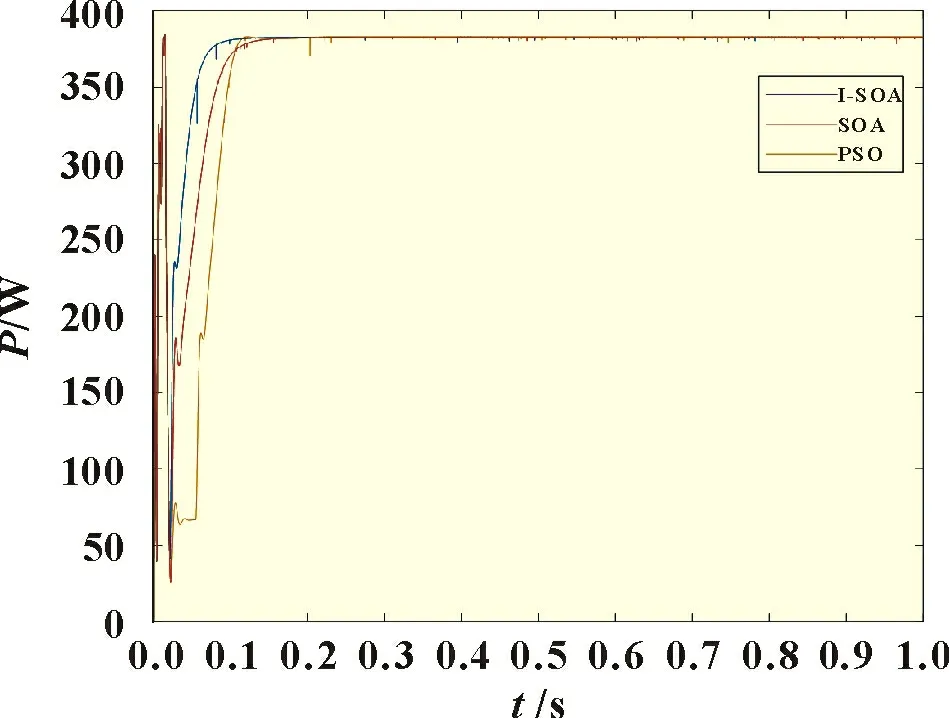
图7 静态条件下的仿真结果

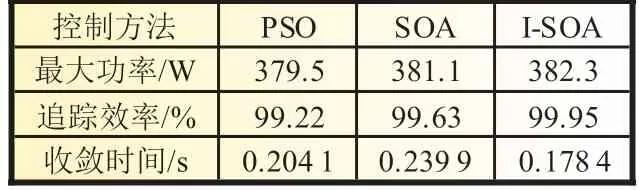
表2 三种算法运行结果对比

4.2 动态条件下的仿真分析

由于环境和天气因素的影响，光伏阵列受到的光照强度会随时发生改变，因此进行如下仿真实验：PV1为1 000 W/m2，PV2 为800 W/m2，PV3 为400 W/m2，在0.5 s 时，PV1 受到的光照强度从1 000 W/m2下降到400 W/m2，仿真结果如图8 所示。环境在0.5 s 发生突变时理论最大功率为245.8 W(由图3 知)。I-SOA 算法在0.733 4 s 收敛到了最大功率244.9 W，与理论值245.8 W 仅差0.9 W，追踪效率为99.63%；SOA 算法和传统的PSO 算法追踪最大功率失败，陷入了局部最优。

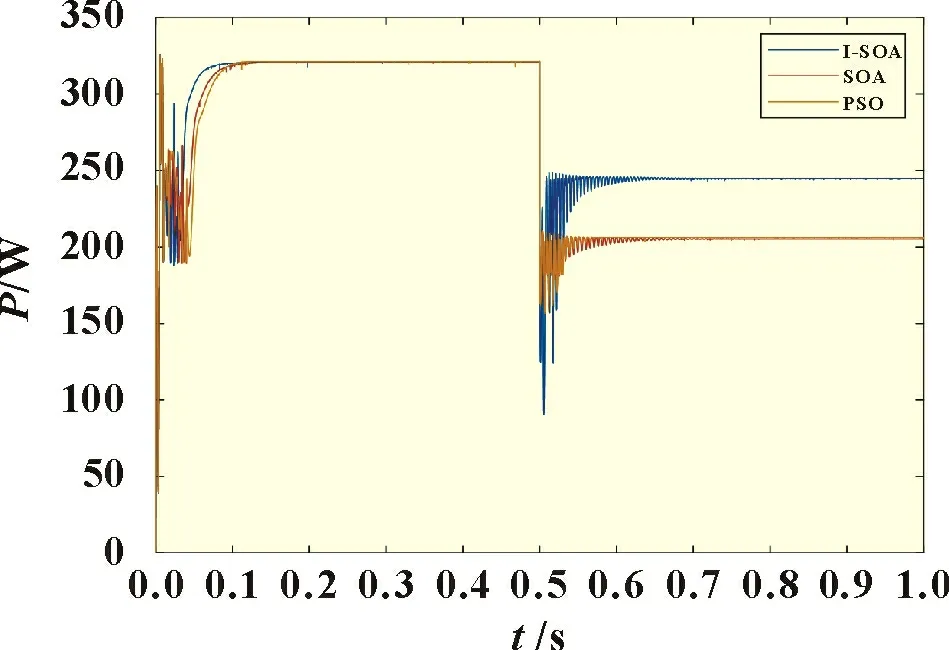
图8 动态条件下的仿真结果

仿真结果表明，I-SOA 算法可在动态条件下成功搜索到全局最大功率点，并且可以稳定输出功率。

5 结论

本文提出了一种改进海鸥优化算法的MPPT 控制方法，针对SOA 全局优化搜索过程为线性、易因过早收敛而陷入局部最优的问题进行改进。对SOA 的附加变量因子进行非线性处理，以适应光伏P-U 曲线呈现的非线性特征；引入混沌序列，增加种群位置的多样性，提高算法跳出局部最优的能力。在Matlab/Simulink 中搭建模型，在不同环境下与SOA、PSO进行仿真对比，结果表明，本文提出的改进海鸥优化算法的MPPT 控制方法可以快速准确地跟踪到全局最大功率，极大地提升了光伏利用效率，具有实际应用价值。