基于RCMDE与概率神经网络的滚动轴承故障诊断

陈 帅，黄晋英

（中北大学 机械工程学院，太原 030051）

0 引言

滚动轴承作为机械设备的重要部件之一，因其复杂的结构和恶劣的工作环境，在长时间运行后可能会出现各种各样的故障，结果可能导致企业生产效率降低严重时甚至出现生命安全问题[1]。所以，对其故障诊断方法进行系统全面的探究具有十分重要的实际意义。如果发生了故障，相关的振动信号往往会具有非平稳以及非线性等方一系列特征。现有的非线性、非平稳性以熵值为特征参数的信号分析方法主要有：近似熵、排列熵、模糊熵、样本熵等，但上述方法均为基于时间序列的单一尺度分析，分类效果较差[2]。之后又提出了多尺度熵算法，其优点是通过多尺度粗粒化过程使得熵扩展到多个时间尺度上，从多尺度表征故障信号的特征信息，进而解决了单一尺度熵的局限性，减小了偏差[3]。但是当数据序列较长时，会出现运算速度慢、故障信息丢失严重等问题，基于此，学者们提出一种精细复合多尺度散布熵（RCMDE）算法[4]，该方法能够明显改善在粗粒化过程中信息丢失问题。近年来，神经网络已经获得了广泛的应用，它在非线性关系数据的处理领域中尤其显著的优势。概率神经网络（PNN）的主要特点是有良好的并行处理、自学习以及自组织等方面的能力，可以在不同的精度水平之下向各种连续非线性函数进行逼近[5]。在此基础上，本文以概率神经网络（也就是PNN）以及精细复合多尺度散布熵（也就是RCMDE）为基础首次提出了一种新的滚动轴承故障诊断分析方法，在研究的过程中，还和MDE-PNN法展开全面的分析与对比。所得到的结果表明，所提方法既能够实现轴承故障的有效识别分类，且诊断效果优于MDE-PNN方法，平均分类精度达到了97.65%。

1 精细复合多尺度散布熵理论基础

1.1 散布熵

散布熵是度量时间序列复杂性的非线性动力分析方法，对于长度为N的时间序列x=｛x1，x2，…，xN｝，其计算步骤如下[6]：

1）利用正态分布函数将时间序列x映射到y=｛yj，j=1，2，…，N｝，yi∈(0,1)，如式(1)所示。

式(1)中，σ和μ分别表示标准差和均值。

2）线性变换将y映射到[1，2，…，c]，如式(2)所示。

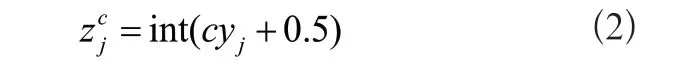
式(2)中，c是类别个数，int()是取整函数。

3）计算嵌入向量zm，ci：

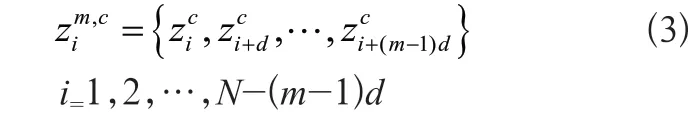
式(3)中，m是嵌入维数，d是时间延迟。

7)计算标准散布熵，公式如式(7)所示。

1.2 精细复合多尺度散布熵

RCMDE计算过程如下[7]：

1）多尺度粗粒化。给定原始数据u，其第k个粗粒化序列的计算如式(8)所示。

式(8)中，τ是尺度因子。

2）对每个尺度τ，RCMDE值定义如式(9)所示。

2 概率神经网络

它为径向基网络当中的重要分支，主要的优点就是分类精度比较高，可以有效地利用简单的线性模型训练非线性模型，有效避免了BP神经网络的局部最小值问题[8]。

PNN模型分为4层结构，第1层是输入层，第2层是具有N个神经元的隐含层（N是训练数据的数量），第i类样本的第j个神经元的输入与输出关系由式(10)确定[9]。

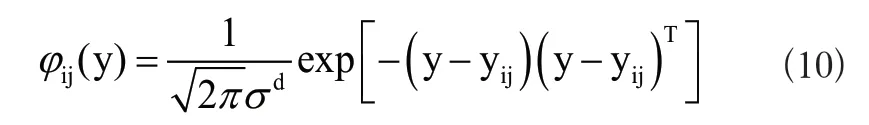
式(10)中是平滑因子，d为数据维度。

第3层是求和层，其把上一层中为同类的隐含层神经元的输出按式(11)平均：

式(11)中，fi为第i类的概率。

第4层是神经元的输出层，如式(12)所示。

式(12)中，z为输出层的输出。

3 实验验证

3.1 实验设置

在本研究中将会通过西储大学数据集来进行全面的分析与验证。所采用的实验台详见本文的图1，其中有电子控制器、功率测试分析设备、扭矩传感器以即电动机等多个重要的组成部分。轴承选用SKF6205-2RS，为了模拟轴承常见的4种状态，采用电火花加工方式对轴承进行不同程度的单点损伤。选择采样频率12kHz、电机转速为1797r/min的驱动端轴承数据进行分析，每种状态选择80个样本，共计320个样本，每个样本长度为4096，轴承状态说明见表1。图2为轴承时域波形图。

图1 实验台

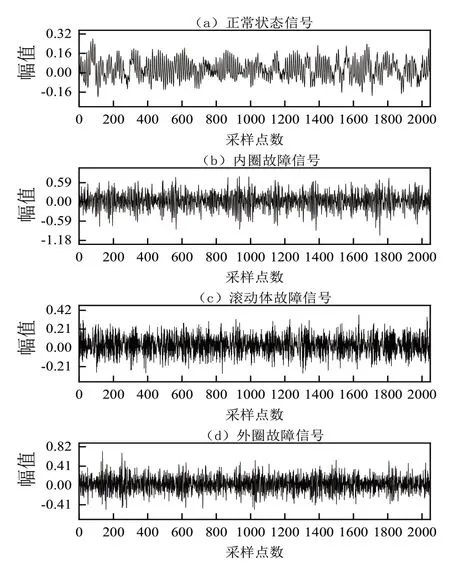
图2 轴承4种状态时域波形图

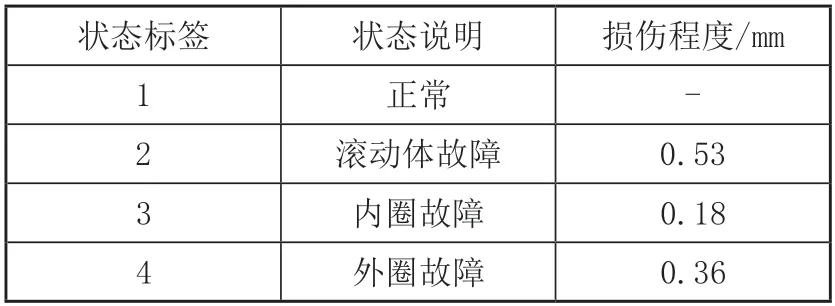
表1 轴承的4种状态

3.2 实验结果

计算320个样本的RCMDE值，设置算法相关参数：最大尺度因子τ=20，嵌入维数m=2，延迟时间d=1。每种状态不同样本计算的熵值均值如图3所示，可知，正常轴承振动信号RCMDE值远大于3种故障状态RCMDE值，并且变化趋势明显不同。对于排在前面的三个尺度，正常情况下，RCMDE值会随着尺度逐渐提高而相依地提升，如果是出于故障的状态中，那么它将会是始终下降的，尤其是由第三个尺度至第十个的过程中，将出现一定程度的波动现象，在此之后将比较的稳定。从整体上来看，RCMDE值与尺度因子成反比，在尺度因子达到11之后逐渐趋于平稳。

图3 振动信号RCMDE均值

此外，还与MDE法展开全面的对比分析，以阐述RCMDE法所具有的主要优势。计算每种状态信号不同样本MDE值，所得结果如图4所示。对比图3、图4，可以看出：随着尺度因子τ的增大，RCMDE值变化较MDE值变化相对平缓，从图4可知，外圈和内圈故障从第5个尺度因子之后基本重合，不利于下一步分类器的识别分类，所以，选择RCMDE值作为特征参数进行轴承4种状态的特征提取较为合理。

图4 前20个尺度MDE均值

实验随机选取每种状态的50个样本作为训练样本，30个样本作为测试样本，为了减小实验偶然性，对RCMDEPNN和MDE-PNN两种模型分别进行10次实验，结果如图5所示。根据图5可知，基于RCMDE-PNN的故障诊断方法分类效果明显优于比MDE-PNN方法，分类准确率达到97.65%，而MDE-PNN的分类准确率为92.85%，分类准确率提高了4.8%。

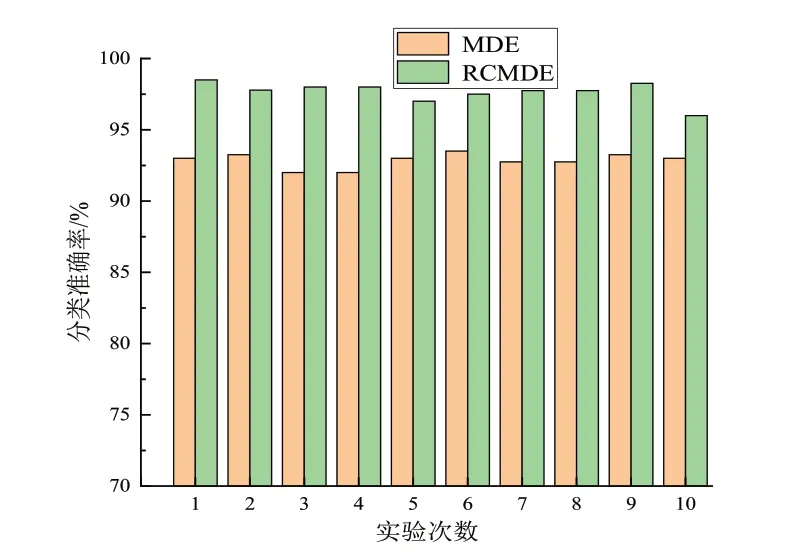
图5 实验结果

4 结语

1）引入一种检验振动信号复杂性的算法-精细复合多尺度散布熵（RCMDE），与MDE方法相比，RCMDE解决了单一尺度熵的局限性，实现了多尺度表征故障信号的特征信息，有利于下一步的故障识别分类；

2）RCMDE-PNN模型的轴承故障诊断准确率为97.65%，而MDE-PNN模型诊断准确率仅为92.85%，本文所提RCMDE-PNN方法，提升其分类准确率达4.8%，并且对它的优势与有效性进行了全面的验证。