基于改进融合蚁群算法的机器人路径规划方法研究

赵天亮，张小俊，张明路，于方程

（河北工业大学 机械工程学院，天津 300401）

0 引言

随着人工智能领域的繁荣，机器人进入了高速发展阶段，提升智能化程度成为了机器人目前追求的高级目标，其中路径规划是指在环境条件已知或未知的情况下，机器人从起始点目标点规划出一条能耗低，距离短，时间少的安全无碰撞路径[1]。

路径规划算法包括A*算法、神经网络算法、遗传算法、模拟退火算法、蚁群算法、粒子群算法等。蚁群算法具有良好的适应性和鲁棒性，但也存在冗余节点多、收敛速度慢、易陷入局部最优等问题。本文针对蚁群算法收敛速度慢，冗余节点多，距离障碍物过近，容易陷入局部最优等问题进行了改进，提出了改进融合蚁群算法。将A*算法的启发式搜索思想融入到蚁群算法中，增加起始点和目标点对搜索过程的影响；提出新的最优路径及周边路径信息素更新方式，避免算法陷入局部最优，设置安全值避免出现机器人距离障碍物过近的情况。在Matlab 2020a中完成了传统蚁群算法和改进融合蚁群算法的对比仿真实验，在实验室进行机器人实验，实验结果表明改进融合蚁群算法具有可行性，有效解决距离障碍物过近的问题，规划路径距离更短，规划效率显著提升[2]。

1 蚁群算法

蚁群算法是根据蚁群觅食规律而来的仿生智能算法。在蚁群算法中，第k只蚂蚁从节点i移动到节点j由多个因素决定，包括路径上的信息素的浓度τij、信息素重要性因子α、启发式信息重要性因子β和期望启发式信息ηij。

根据式(1)选择下一个节点：

图1 8邻域节点搜索图

节点i和节点j之间的距离dij为欧式几何距离，欧式几何的距离如式(3)所示。

第k只蚂蚁从节点i 移动到节点j后，留在路径上的信息素会随时间挥发。更新当前最优路径上的信息素浓度，使下一次迭代的蚂蚁倾向于走全局最优路径。更新信息素浓度如式(4)所示。

其中，p(0<ρ<1)表示信息素的挥发水平，1-p的结果表示某-路径上信息素挥发后的残留水平，p越大，信息素挥发速度越快。

△rij;(t)是蚁群中所有蚂蚁释放的信息素之和的增量，表示第k只蚂蚁在t时刻释放的信息素增量，蚂蚁总数为m，信息素增量计算公式如式(5)所示。

式(5)中，Q为蚂蚁在路径上释放的信息素强度，L表示第k只蚂蚁经过搜索得到的全局最优路径长度。

2 A*算法

A*算法核心思想是根据给定的估值函数大小判断搜索路径是否为全局最优路径。其估值函数如式(6)所示。

传统A*算法使用广泛，其规划出的路径存在控制效率低，转折点多等问题。

3 改进融合算法

3.1 优化期望启发式函数

其中hjg表示机器人从当前位置j运动至终点g时的代价函数，将式(9)带入状态转移概率式(1)，改进后的状态转移概率如威(10)所示。

3.2 改进信息素更新方法

随着蚁群搜索代数增多，地图.上残留的蚁群信息素越来越多，这就导致第N次蚁群搜索时容易出现局部最优的情况[3]。为了避免原始蚁群算法陷入局部最优问题，本文提出一种基于自我调节的信息素更新方式:当第N-1波蚁群完成觅食后，不仅更新当前情况下最优路径上残留的信息素浓度，还更新当前情况下最优路径周围的可通行路径上残留的信息素分布情况，再投放第N波蚂蚁。自我调节式的信息素更新方法如式(11)所示。

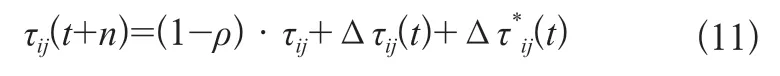
更新当前情况下最优路径上的信息素浓度时如式(12)所示。

其中:n表示当前情况下最优路径_上的信息素浓度改变程度，0<1<1,2越大，变化程度越高。

其中:n表示当前情况下最优路径_上的信息素浓度改变程度，0<1<1,2越大，变化程度越高。

其中，y表示周围的可通行路径信息素浓度变化程度，γ∈N,距离最优路径越近，y的取值越大，信息素浓度变化程度越高，γγ也会相应减小;相反，距离当前最优路径越远，此路径上信息素浓度变化程度越低。

算法更新后，机器人最优路径及其周围可通行路径上的信息素浓度随着迭代次数的增加进行不同比例更新，在迭代过程中根据上一代蚁群残留的信息素浓度进行自我调整，能更快地找到最优解。

3.3 设置选择概率因子

传统蚁群算法存在容易陷人局部最优解的缺点，容易找到局部最短的路径，而忽略全局最优路径。设选择概率因子为q。和随机数因子为q。此时算法选择下-一个节点策略满足式(14)所示。

3.4 设置安全值

传统蚁群算法在规划机器人路径时会出现如图2所示的情况，灰色节点为障碍物节点。在实际应用中，机器人从A点走到B点的过程中会途径C点，在C点会出现机器人距离障碍物过近的情况。为了提高运动安全性，本文提出采用设置安全值的方法实现避障。

图2 机器人经过障碍物

改进后的蚁群算法从起始节点出发，将起点周围所有可移动的节点都放进Openlist表中，根据状态转移概率选出最小值的节点x放进Closelist表中，同时将此点作为下一个移动节点。如图3所示，r为增设的安全值，表示路径上的点距离障碍物的长度，根据此地图信息，其此值设置为0.707，当出现r＜0.707时，则通过判断障碍物位置增加额外距离。将此点从Closelist表中删除，并从上一节点开始搜索，重新寻找最新节点，重复上述过程，直到找到符合安全值的点。

图3 设置安全值

设置安全值会增加转折点数量，为了消除这一影响，利用上述回溯法重新计算其父节点的可移动节点，并且从剩下的节点中根据状态转移概率找到一条从起点到当前节点的路径。

为了保证路径的平滑，当节点更新时，需要将其父节点同时更新。采用回溯法重新计算其父节点的可移动节点时，从余节点中根据式(14)找到新的路径。重新布线可减少冗余节点。如图4所示，在圆心为C半径为r的圆内存在A点和B点，通过式(3)计算A到B到C的代价和B到C的代价，如果f(A-C)＞f(B-C)，那么选取B作为父节点，如果f(A-C)＞f(B-C)，选取A作为父节点。为进一步优化路径，参考RRT算法中重新布线的思想，计算总代价值，确定是否重新布线。

图4 回溯法

综上所述，改进融合蚁群算法流程如图5所示。

图5 改进融合蚁群算法流程图

4 实验验证

4.1 仿真实验验证

本文采用MATLAB R2020a进行仿真实验。首先，建立一个30×30的栅格图。在地图中，障碍物设置为黑色区域，机器人无法通过，可以通过的区域设置为白色。

设置蚁群初始参数，如表1所示。传统蚁群算法和改进融合蚁群算法规划路径如图6、图7所示。根据环境特点，设置起始点为（15，1），途径两个点（25，25），（5，25），最后回到起始点。

表1 改进融合蚁群算法参数

图6为传统蚁群算法仿真路径图，图7为改进融合蚁群算法仿真路径图；图8为传统蚁群算法的收敛曲线图，图9为改进融合蚁群算法的收敛曲线图，其中，上方的曲线代表平均路径长度，下方的曲线代表最小路径长度[4]。

从图6可以看出，使用传统蚁群算法进行路径规划时，路径转折点多，路线出现多处距离障碍物过近的情况，在x=7，y=23处，出现局部最优的情况。从图7中可以看出，相同环境下，相比于传统蚁群算法，改进融合蚁群算法转折点明显减少，路径更平滑，未出现局部最优情况，全局路径未出现距离障碍物过近的情况。

图6 传统蚁群算法路径规划

图7 改进融合蚁群算法路径规划

图8、图9为传统蚁群算法和改进融合蚁群算法在栅格地图下的收敛曲线，上方曲线代表每次迭代过程搜索出来的平均距离，下方曲线代表每次迭代过程搜索出来的最小距离。图8为传统蚁群算法收敛曲线，可知最小路径迭代到50代附近趋于平稳，搜索出来的最优路径长度为90，拐点数目为25。图9为改进融合蚁群算法收敛曲线，可知蚁群最小路径迭代到36代附近趋于平稳，搜索出来的最优路径长度为85，拐点数目为15。

图8 传统蚁群算法收敛曲线

图9 改进融合蚁群算法收敛曲线

相同环境中对传统蚁群算法和改进蚁群算法各进行20次仿真实验，表2分别列出了传统蚁群算法和改进融合蚁群算法在平均路径长度，平均收敛速度，平均拐点数目和平均运行时间方面的对比[5]。

表2 两种算法仿真结果对比

20仿真实验结果表明，改进融合蚁群算法具有可行性，且和传统蚁群算法相比，改进融合蚁群算法搜索的平均路径长度从93.21减少到88.91，减小22.2%，迭代次数从平均迭代49代减小到平均迭代38代，收敛速度提升51.4%，平均拐点数目从27个较少到15个，减少40%，平均运行时间从12.36s减少到10.25s，减少25.8%。其中，第9次和第16次改进融合蚁群算法出现平均搜索时间过长的情况，因为设置了安全值，使得单只蚂蚁搜索时间略有增加，将信息素重要性因子á从1.2调节为1.3即可改善这种情况。

4.2 基于ROS系统的机器人实验验证

采用基于ROS系统的机器人作为平台进行实验。如图10所示，此平台包括深度摄像头、思岚A1激光雷达、超声波传感器等硬件，其整体架构如图11所示。

图11 机器人硬件架构图

图10中，通过深度摄像头和思岚A1激光雷达联合扫描建立地图模型，并将点云图转换栅格地图。传感器接收到环境信息后，由串口传递给计算机。计算机处理信号转化成位置信息及运动指令，并将运动指令通过串口发送给STM32控制板，控制板发送运动指令给左右电机驱动器，实现运动控制。

图10 基于ROS系统的机器人

机器人中传感器型号如表3所示。

表3 传感器型号

实验采用的软件系统中，路径规划算法以插件的形式嵌入在“move_base”模块中。在“move_base”模块中将系统原有的A*算法替换为上述改进融合蚁群算法，设置实验参数和仿真实验相同。此实验中输入量包括静态环境信息，摄像头信息，激光雷达信息，设定好的坐标变换信息和机器人目标位姿。其中静态环境信息在实验前使用SLAM激光雷达扫描生成。系统内置轨迹跟踪模块，设定相同的起点和终点，蚁群算法和改进融合蚁群算法路径规划过程如图12和图13所示，实验结果如图14和图15所示，在机器人上对两种算法分别进行20次路径规划实验，实验平均数值如表4所示。

图12 传统蚁群算法实验过程

图13 改进融合蚁群算法实验过程

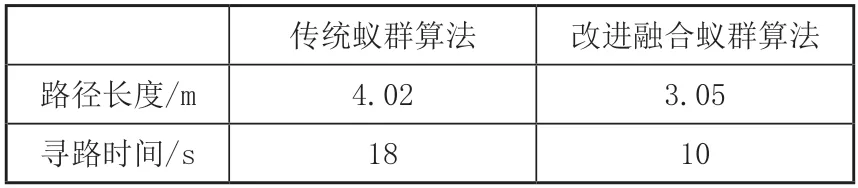
表4 两种算法实验结果对比

图14可以看出，将传统蚁群算法应用在机器人路径规划实验时，规划路径长，转折点多，并非最佳路径。从图15可以看出改进融合蚁群算法规划出的路径转折点减少，曲线更加平滑，路径长度明显减小，和障碍物保持合适的距离，机器人行走更加平稳。

图14 传统蚁群算法路径规划图

图15 改进融合蚁群算法路径规划图

20次实验平均结果表明，在相同环境下，改进融合蚁群算法能完成路径规划任务，路径较为平滑，转折点少，未出现局部最优及距离障碍物过近的情况，具有可行性。传统蚁群算法规划路径长度为4.02m，寻路时间为18s，改进融合蚁群算法规划路径为3.05m，寻路时间为10s。两者相比，改进融合蚁群算法规划的路径更优，路径长度减少了24%，寻路时间减少了44.4%，将改进融合蚁群算法应用在机器人上，会使机器人路径规划性能明显提升。

5 结语

传统蚁群算法进行全局路径规划时存在冗余节点多，收敛速度慢，距离障碍物过近等问题。本文研究目的为改善传统蚁群算法上述问题，提高路径规划性能。在传统蚁群算法的基础上，融合了A*算法的启发式搜索策略，提出改进融合蚁群算法。首先，设置了选择概率因子，提高了算法收敛速度；其次，引入自我调节机制对迭代过程中的最优路径及周围的信息素进行更新，改善了可能出现的局部最优解的情况；设置了安全值避开了障碍物边界，避免在实际应用中出现距离障碍物过近的情况。在Matlab中使用栅格法搭建环境模型，实验表明，在同一环境下，改进融合蚁群算法在路径长度，收敛速度，拐点数目，运行时间方面均优于传统蚁群算法。最后将传统蚁群算法和改进融合蚁群算法应用在机器人中，通过结果对比可以看出，在全局路径规划中，改进融合蚁群算法能高效，准确，快速地搜索出安全路径，转折点更少，路径更平滑，搜索时间更少，不会出现局部最优的情况。下一步工作设置更多工况进行仿真实验，进一步优化改进融合蚁群算法。