黏弹性表面活性剂溶液中颗粒沉降特性研究
2022-05-26苏晓辉张弛徐志锋金辉王治国
苏晓辉,张弛,徐志锋,金辉,王治国
(1 西安石油大学机械工程学院,陕西西安 710065; 2 西安交通大学动力工程及多相流国家重点实验室,陕西西安 710049)
引 言
黏弹性流体悬浮颗粒流广泛存在于自然界和工业生产制造过程,如生物体液中细胞运动[1-2]、聚合物和日化用品加工、油气藏水力压裂[3-4]、微流控装置中颗粒的连续操控与分离[5-8]。表面活性剂溶液达到一定浓度时表现出很强的黏弹性,具有独特的流变学性质,在工业生产和制造领域受到广泛关注。研究人员[9-10]发现多元聚合物-表面活性剂中表面活性剂的用量对于原油乳状液的稳定性具有重要影响,溶液弹性能够有效提高驱油效率。此外,表面活性剂溶液具有湍流减阻、强化传热作用,在流体管道输送和换热领域也得到了广泛应用[11-12]。由于其强非线性应力应变率特性和应力松弛效应,表现出十分复杂的流动现象[11]。当黏弹性表面活性剂溶液中有颗粒存在时,体系的流动特性更为复杂,例如颗粒在其中沉降时颗粒速度的“过冲”现象[13],颗粒沉降速度的持续波动[14-16]等。目前对于具有复杂流变性质的黏弹性表面活性剂溶液中颗粒沉降规律仍缺乏清晰的认识,颗粒所呈现的复杂沉降现象背后的机理尚不明确。
黏弹性流体中颗粒沉降特性取决于流体的流变性质以及操作条件。国内外学者[17-23]针对黏弹性流体中颗粒运动特性开展了相关研究,主要集中于剪切条件下流体中颗粒横向运移以及成链特性,探索了颗粒宏观运动与流体流变性质之间的关系。颗粒群在流体中运动主要取决于流体作用于颗粒的曳力,为此学者们[24-25]对黏弹性溶液中颗粒曳力进行了研究,发现弹性(用Deborah 数De=λu/a来表征,其中λ为松弛时间;u为流体特征速度;a为特征尺寸,取颗粒半径)对颗粒曳力具有显著影响,在常黏度的Boger 流体中,曳力随着De增加先减小至某一最小值后又增加,而在剪切稀化流体中,曳力随着De单调减小,并且减小速度和幅度与剪切稀化的强度相关。基于此,提出了黏弹性流体中颗粒曳力理论公式,用于描述两相流动相间动量交换[24,26]。此外,对黏弹性流体中颗粒沉降特性开展了研究[2,27]。有学者[13,28-30]采用虚拟区域法研究黏弹性流体中单颗粒和多颗粒的沉降特性,发现流体弹性和壁面效应均会影响颗粒沉降,他们均采用只考虑黏弹性的Oldroyd-B 本构模型。Oldroyd-B 本构模型由于可以简洁明确地描述流体的黏弹性,在涉及描述表面活性剂溶液体系的研究中得到了广泛应用[10,13]。
然而,实际工程中的黏弹性表面活性剂溶液,不仅具有时间松弛效应,其应力应变率响应也具有非线性特性,如剪切稀化、拉伸硬化和剪切带等,其对颗粒沉降也有显著影响。学者们[14-15,31]通过实验对一定浓度下的表面活性剂溶于水后形成的蠕虫状胶束溶液中颗粒沉降进行研究,发现颗粒在这种黏弹性溶液中沉降速度呈现随机波动,不能达到稳定的终端速度,并且认为这一现象与颗粒尾迹区的复杂拉伸应变特性相关。Wang 等[16]也在实验中发现了这一效应,并且发现在某些条件下,不仅颗粒速度在沉降过程中随机波动,颗粒沉降方向也发生了变化,即颗粒在流体中出现了沉降-反弹的弹跳现象,认为这一现象与此类蠕虫状胶束流体的流变性质密切相关[3-4,32],推测颗粒沉降过程中下游的“负尾迹”可能是引起颗粒沉降速度波动的原因,因此有必要对其机理展开研究。
本文采用同时考虑表面活性剂溶液黏弹性和剪切稀化及拉伸硬化效应的FENE-P 模型以及考虑了大分子之间相互作用的用于浓表面活性剂溶液的Giesekus模型,研究颗粒在其中的沉降特性,讨论溶液的流变性质对颗粒沉降特性的影响规律以及颗粒沉降过程中尾迹区的特征,研究结果有助于进一步认识和解释黏弹性表面活性剂溶液中颗粒沉降速度的波动机理。
1 数学模型
考虑颗粒沉降运动过程,为了简化模拟,选取颗粒为参考坐标系,颗粒在沉降过程中受流体曳力以及重力和浮力作用,其运动由牛顿运动定律描述。同时通过非惯性系的体积力将其与描述流体流动的偏微分方程耦合。对于瞬态、不可压缩黏弹性表面活性剂溶液的绝热流动,其控制方程包括连续方程、动量守恒方程以及描述附加弹性应力的黏弹性本构方程。
连续方程

动量方程
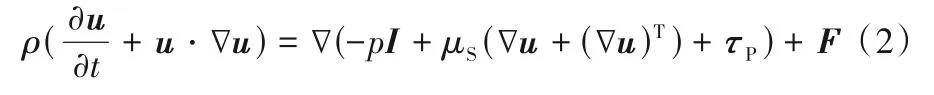
其中,ρ为流体密度;u为流体速度;p为流体压力;μS为溶剂黏度;τP为附加黏弹性应力,由黏弹性流体的本构方程确定;F为流体在非惯性系中运动时的惯性力。对于小球参考系,惯性力F只有垂直分量Fz
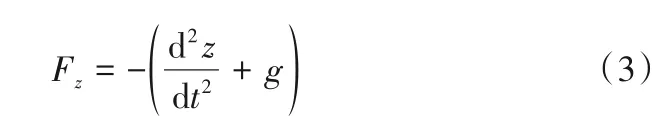
黏弹性本构方程
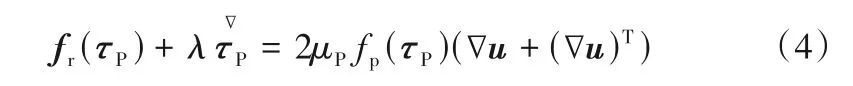
其中,λ为松弛时间;μP为溶质黏度;fr为松弛函数;fp为黏度系数。对于不同的本构方程,fr和fp具有不同的形式。
上随体导数
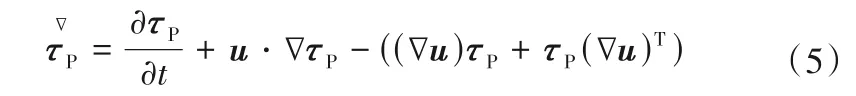
Oldroyd-B本构方程

Oldroyd-B 模型把大分子溶液看作是牛顿溶剂流体中悬浮的胡克弹簧体系构成,由分子动力学理论推导而来,可用来预测基本的黏弹性特征,但是其假定黏度为常数,并且可以无限拉伸,因而在拉伸流动中常常得到不符合物理实际的结果,是比较简单的一种黏弹性模型。
FENE-P本构方程
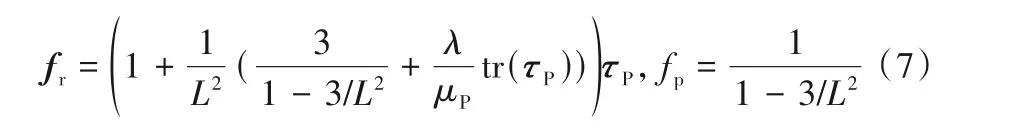
其中,L为伸长率。
FENE(finitely extensible nonlinear elastic)模型也是基于分子动力学理论,但是将大分子看作是非线性弹簧,并且考虑了大分子的有限拉伸率。基于FENE模型的Peterlin封闭模型同时考虑了大分子有限拉伸以及流体剪切稀化效应。
Giesekus本构方程
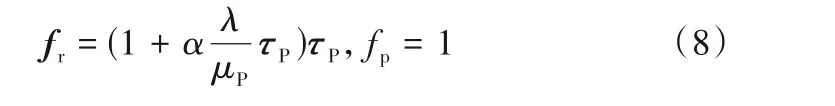
其中,α为迁移因子。
Giesekus 本构模型用于描述半稀和浓溶液,考虑了大分子之间相互作用产生的流动阻力,因此方程中增加了二次非线性项。
颗粒运动由牛顿运动定律确定

其中,m为颗粒质量;z为颗粒位移;Fz为流体对颗粒的作用力;Fg为颗粒重力。
流体对颗粒曳力为
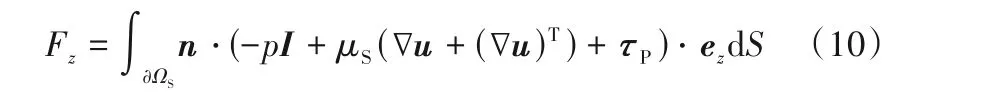
其中,I是单位张量;n为球表面的单位法向量;ez为流体流动方向单位矢量;∂Ωs是球形颗粒的外表面积。
颗粒所受重力为
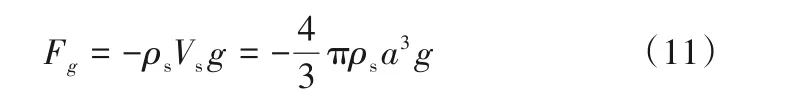
其中,ρs为颗粒密度;Vs为颗粒体积;a为颗粒半径。
雷诺数和维森贝格数定义为
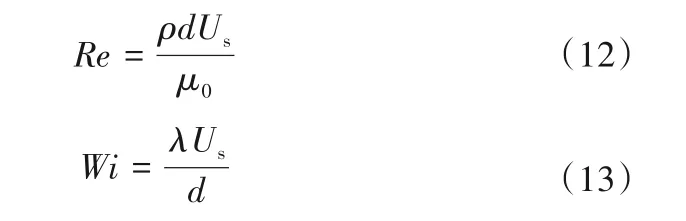
其中,d为颗粒粒径;零剪切黏度μ0=μS+μP;特征速度Us取小球的瞬时沉降速度。
2 数值模拟方法
模拟流动区域和计算区域如图1所示,半径为a的球形颗粒位于半径为R的圆柱体容器的对称轴上,颗粒在重力、浮力和曳力作用下从静止开始沉降,竖直方向上瞬时沉降速度为Us,初始时刻t=0 s时沉降速度Us=0。由于取运动颗粒自身为参考系,那么对于计算域的流体运动只需考虑流体相对于颗粒的运动即可,颗粒相对于流体具有平均速度Us,因此在远离颗粒的计算域入口处流体相对于颗粒参考系的速度u=Us,即流体从计算域下方入口∂Ωin以颗粒瞬时沉降速度Us均匀垂直满流流入,从上方出口∂Ωout流出,模拟中通过改变通道阻塞比a/R表征壁面对颗粒沉降的影响,考虑到流场的对称性,只需求解如图1所示的二维轴对称流动,然后通过周向旋转即可得到三维的颗粒在流体中沉降的流场。
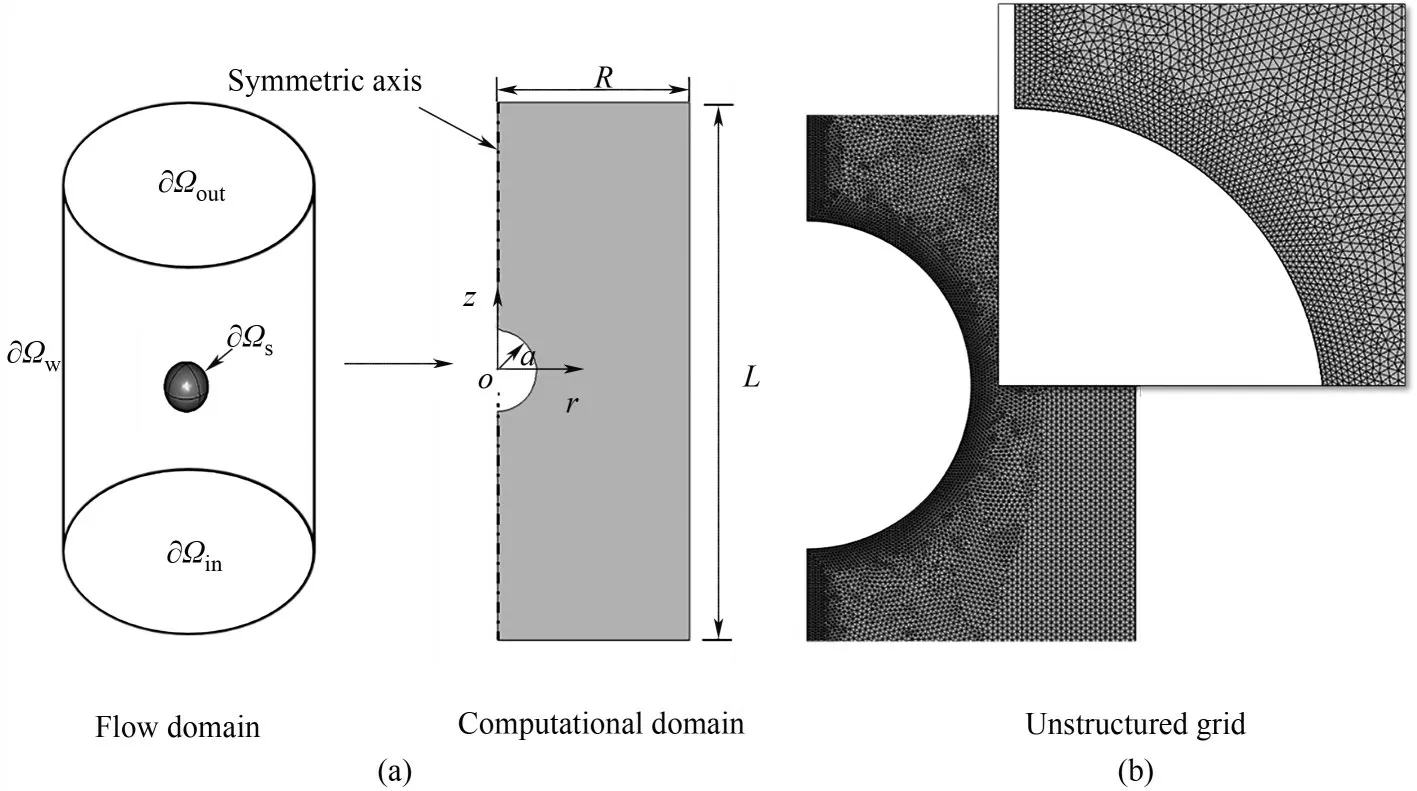
图1 数值计算选取的流动区域和计算区域Fig.1 The flow domain and computational domain for numerical simulation
采用有限元软件COMSOL 的弱形式对控制方程进行求解,采用混合Galerkin 方法对偏微分方程进行离散,对速度分量采用二次形函数,对压力和黏弹性应力采用一次形函数。通道入口和壁面采用恒定速度u=u(U,0,0)和零压力梯度∇p=0,出口采用压力出口,颗粒表面流体速度u=u(0,0,0),压力梯度∇p=0。对于黏弹性应力,入口处为均匀速度,出口处充分发展,黏弹性应力分量为零。容器壁和颗粒表面处溶液中表面活性剂分子只对壁面产生切向应力,其法向应力满足n(n·τP)=0,n是边界的单位法矢量。
3 流体流变参数拟合及颗粒沉降模拟
采用控制应力流变仪(HAKKE-RS300)对黏弹性表面活性剂溶液[(2.8%(质量)OTAC 和0.56%(质量) NaSal)]的线性黏弹性和稳态流变进行实验研究,结果如图2 所示,由小幅振荡剪切实验结果,可以获得溶液流变参数松弛时间λ,通过稳态剪切实验结果可以获得表征剪切稀化效应的参量如Giesekus 模型中迁移因子α和FENE 模型中的拉伸率L,实验获得溶液流变参数的方法详见文献[16]。通过实验发现流体具有剪切稀化效应,根据线性黏弹性,松弛时间λ=0.27 s,μ0=1.944 Pa·s,G0=7.285 Pa,采用Giesekus 本构模型进行参数拟合,拟合结果如图2(a)所示,采用此流变参数对颗粒沉降进行模拟,颗粒半径a为0.003 m,容器半径R为0.031 m,颗粒密度ρs=7800 kg·m-3,对比不同迁移因子时的结果,模拟所得颗粒沉降速度随时间的分布如图2(b)所示,可以看出,表面活性剂溶液中颗粒沉降速度随时间的变化明显不同于牛顿流体,α较小时(剪切稀化作用较弱),颗粒沉降初期速度出现了明显的波动性,随着α增加,剪切稀化作用增强,颗粒沉降速度不稳定性减弱。
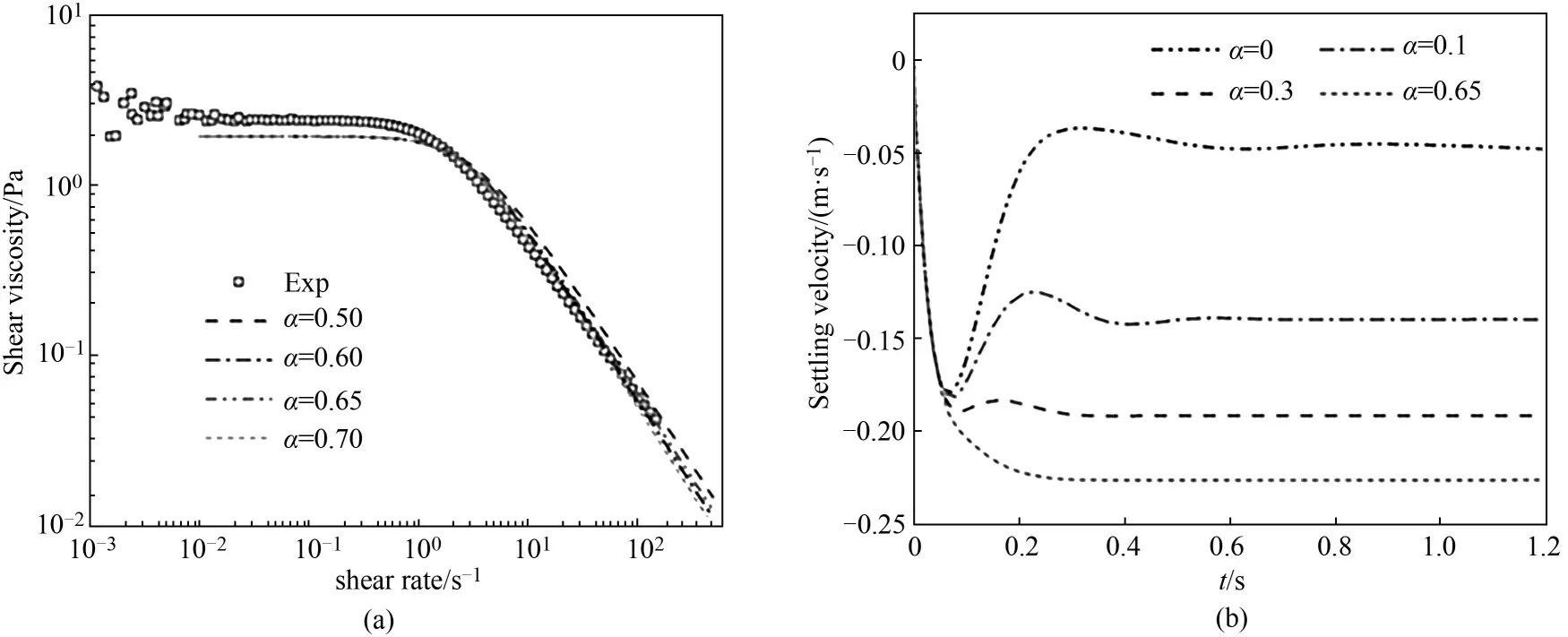
图2 黏弹性表面活性剂溶液(2.8%OTAC+0.56%NaSal)流变性质实验数据及Giesekus本构模型拟合结果(a);颗粒沉降速度随时间的分布(b)Fig.2 The rheological properties from experiments for viscoelastic surfactant solution (2.8%OTAC+0.56%NaSal)and the data fitting using Giesekus constitutive equation(a);The variation of settling velocity of a particle with time(b)
4 模型验证
首先进行网格无关性验证,考虑到球表面附近速度和应力梯度较大,在球表面处采用不同密度的网格M1、M2和M3,对应球表面网格数量分别为106、160 和320,总 网 格 数 量 分 别 为71818、106238 和112613,图3 所示为采用不同网格数量时颗粒瞬时沉降速度的计算结果,可以看出,所采用的网格均可以很好地捕捉颗粒沉降的物理特征,通过对比颗粒沉降终速发现,采用M2网格相对于M1网格的颗粒沉降终速相对变化量为0.03%,而M3网格相对于M2网格的颗粒沉降终速相对变化量小于0.01%,据此采用M2网格作为计算网格,认为进一步加密网格对于模拟结果的影响可以忽略,对于不同a/R,球表面附近网格数量始终取160,而对远离颗粒的区域采用相对较粗的网格,既能保证计算结果的精度,又能显著减小计算量。
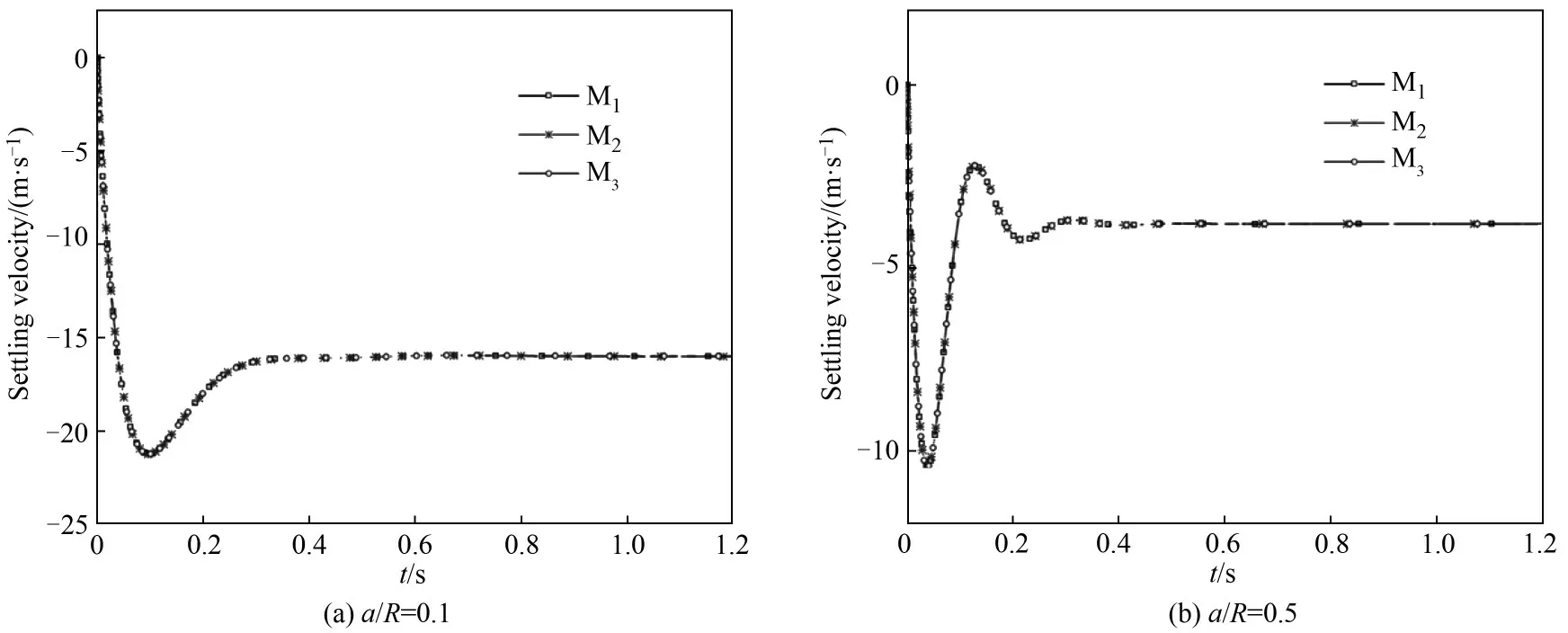
图3 网格无关性验证Fig.3 Grid independence verification
通过本研究模拟结果与前人研究对比,验证本文采用的模拟方法的准确性。对比结果如图4 所示,采用的本构方程为Giesekus模型,为了与文献已有的结果(采用Oldroyd-B 模型)对比,假定本构方程中迁移因子α为0,此时,Giesekus 模型退化为Oldroyd-B 模型,可以看出,采用三种不同通道阻塞比a/R为0.1、0.2和0.5时,模拟获得的颗粒沉降速度随时间的变化与文献中结果吻合较好,说明了本研究采用的模拟方法是可靠的。
由图4可以看出,阻塞比a/R显著影响颗粒沉降速度,当a/R为0.1 时,颗粒沉降速度在t=0.1 s 处出现一个明显的过冲,即沉降速度很快增加到一个最大值,而后又逐渐减小,在0.4 s 后达到稳定的终端速度0.16 m·s-1。当a/R增加到0.2时,在t=0.1 s处仍然出现了速度过冲,其速度峰值小于a/R=0.1 时的值,而后速度减小,减小到某个值后,仍然没有趋于稳定,而是随着时间又逐渐增加,在0.6 s 后基本达到稳定的终端速度0.124 m·s-1,其小于a/R=0.1 时的终端速度值。当a/R进一步增加到0.5 时,壁面影响最强,此时在0.04 s处就出现速度最大值0.10 m·s-1,其最大值相对于a/R=0.1时的最大值减小约一半,沉降速度减小到0.022 m·s-1,之后沉降速度又有明显增加,再次达到一个峰值,后又有轻微减小和增加,如此,经过两次波动在0.5 s左右才达到稳定的终端速度0.038 m·s-1,其终速值也远小于a/R为0.1 和0.2 时的终速值。由此说明随着阻塞比a/R增大,即壁面效应的增强,颗粒沉降终速减小,而且颗粒沉降速度不稳定性增强,这是因为壁面效应较强时,颗粒沉降过程中应变率和应力较大,其弹性应力更大,弹性效应表现更为显著,颗粒沉降速度经过波动之后,流体中积聚的弹性能量充分耗散后,才达到稳定的终端速度。
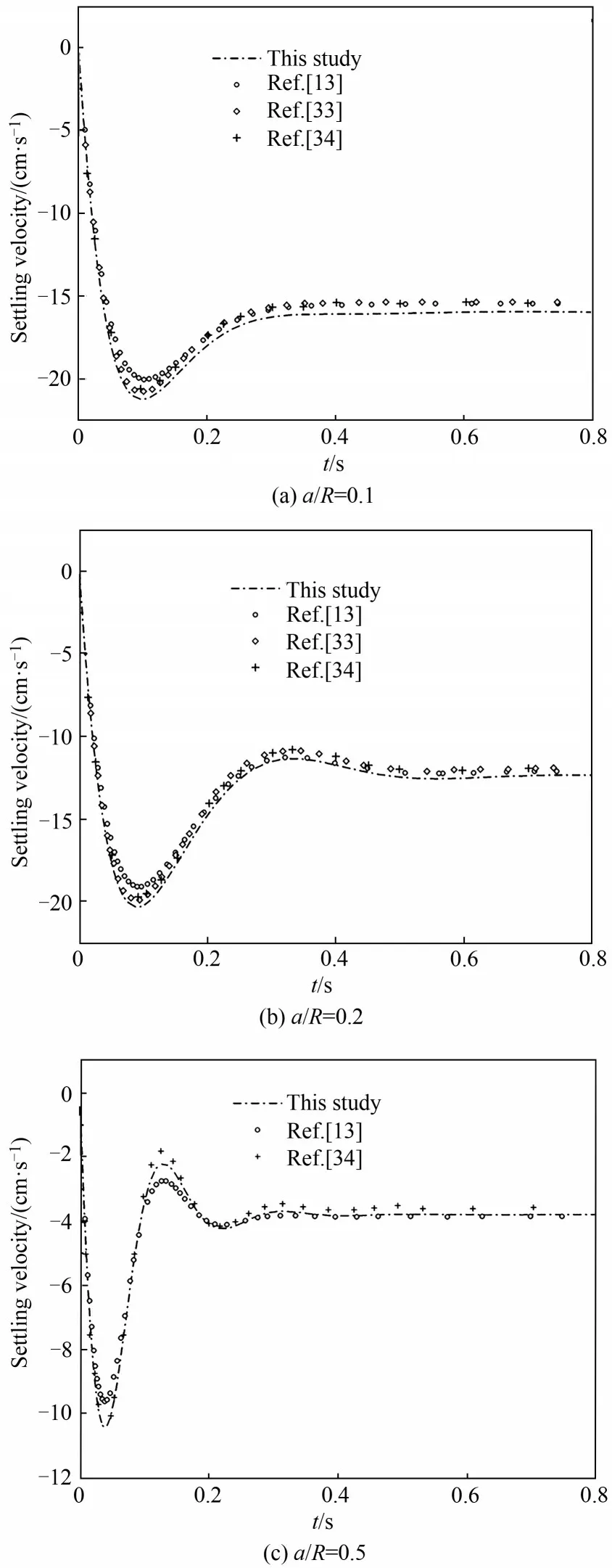
图4 迁移因子α=0时Giesekus流体中颗粒沉降速度模拟结果与文献[13,33-34]对比Fig.4 Comparison of settling velocity of a particle in Giesekus fluids(mobility factor α=0)between present simulation results and literature data[13,33-34]
5 结果和讨论
5.1 Giesekus 和FENE-P 本构模型的流变性质模拟
本文采用的Giesekus 模型适用于半稀和浓溶液,FENE-P 模型适用于稀溶液,两种模型都考虑了剪切稀化效应,为了明晰其流变性质对流体流动和颗粒沉降特性的影响,首先对Giesekus 和FENE-P本构模型的流变性质进行计算,考虑到所采用本构模型的非线性,采用数值方法求解在平面均匀剪切以及单轴拉伸流动下的流体应力分布。首先研究了松弛时间λ对流体剪切和拉伸流变性质的影响,如图5所示,可以看出,松弛时间影响流体黏度曲线关于应变率的分布,当松弛时间较大时,出现剪切稀化和拉伸硬化对应的应变率较小,当松弛时间减小时,出现剪切稀化和拉伸硬化对应的应变率增大,说明了弹性对于应力-应变率的非线性性质也有影响。

图5 松弛时间λ对流变性质的影响Fig.5 The effects of the relaxation time λ on rheological properties
此外研究了两种本构模型中参数对流变性质的影响,如图6、图7 所示,此处采用无量纲化坐标,对剪切流动,横坐标Wi=λγ˙,γ˙为剪切速率,纵坐标τXY为无量纲总剪切应力,对拉伸流动,横坐标Wie=λε˙,ε˙为拉伸速率,纵坐标τXX为无量纲总拉伸应力,其中λ=1.0 s,μS/μ0=0.1。可以看出,对于两种本构模型,在剪切速率0.1 s-1以上,都呈现出蠕虫状胶束溶液的典型的剪切稀化效应,并且同样剪切速率,Giesekus 剪切稀化效应更强,迁移因子α在0.8 以上时,Giesekus 流体出现剪切带。此外,对于拉伸流动,两种本构模型均呈现拉伸硬化的特征,如图6(b)和图7(b)所示。
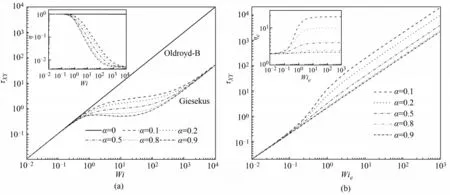
图6 Giesekus流体在平面均匀剪切(a)和单轴拉伸流动(b)时的流变性质(Wi=λγ˙,Wie=λε˙)Fig.6 The dimensionless stress-strain relationships for Giesekus fluids under the planar shear (a)and the uniaxial tension(b)condition (Wi=λγ˙,Wie=λε˙)
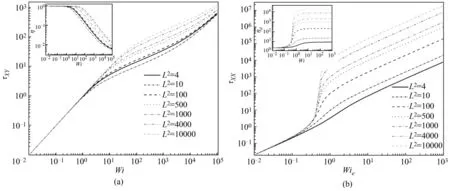
图7 FENE-P流体在平面均匀剪切(a)和单轴拉伸流动(b)时的流变性质(Wi=λγ˙,Wie=λε˙)Fig.7 The dimensionless stress-strain relationships for FENE-P fluids under the planar shear(a)and the uniaxial tension(b)condition(Wi=λγ˙,Wie=λε˙)
5.2 颗粒沉降特性
为了阐明流体流变性质对沉降的影响,先不考虑壁面影响,即a/R趋近于0,为此取圆柱通道的半径R=200a,计算表明,当R/a从150增加到200时,模拟所得颗粒曳力系数只变化了0.1%,据此认为继续增加R/a对计算结果影响可以忽略不计,因此取R/a=200,此时可以看作颗粒在无界流场中沉降,无壁面效应影响。研究颗粒浸没在表面活性剂溶液中运动特性时,认为颗粒为完全润湿[13-16]。此外,需要指出对于实际的颗粒悬浮体系,颗粒群效应和颗粒形状的不规则均会对颗粒沉降特性产生影响,为了简化模型,本研究考虑简单球形颗粒的沉降来解释颗粒沉降的非稳态效应。
5.2.1 流变参数对颗粒沉降速度的影响 在剔除了容器壁面效应的影响后,颗粒沉降速度只受表面活性剂溶液流变性质的影响,因此研究不同De、α以及L对颗粒沉降的影响。
先不考虑剪切稀化效应,即流体本构模型退化为Oldroyd-B 方程,此时颗粒沉降速度随时间的变化规律如图8 所示,取横轴为无量纲时间因子t/λ,纵轴为无量纲速度u/Ut(Ut为斯托克斯沉降速率),当松弛时间λ为0.01 s 时,颗粒整体沉降速度较小,速度的增加较为缓慢,经过较长的时间才能达到一个稳定的终端速度,随着λ增加,颗粒初期沉降速度逐渐增大,这是因为当颗粒沉降过程中对流体施加应变时,由于应力松弛效应黏弹性应力的增加有一个滞后,此时流体应力对颗粒作用力较小,因此沉降速度加速度较大,随着时间增加,应力增加,对颗粒阻力作用逐渐增加,颗粒加速度逐渐减小,初始阶段的应力松弛效应,导致了流体中沉降时颗粒速度的过冲现象,因此弹性效应是造成颗粒沉降不稳定性的原因。λ增加至0.05 s时,颗粒沉降速度出现了轻微的过冲现象,当λ继续增加时,颗粒沉降速度过冲幅度显著增加,并且波动周期数也增加,这在壁面约束时的颗粒沉降速度分布(图4)上更加明显。由无量纲时间看出,随着λ增加,过冲量达到最大值的无量纲时间越小,达到终速的无量纲时间越小,这是由于随着λ增加,流体弹性应力松弛效应增强,颗粒沉降过程中,流体发生变形后相应的变形应力增加缓慢,作用于颗粒的曳力增加缓慢,导致颗粒初始加速度和速度较大,因此产生较为明显的速度过冲。这说明颗粒在沉降初期的不稳定性主要是由流体自身的弹性效应引起,弹性效应越强,颗粒沉降速度随时间不稳定性越强。
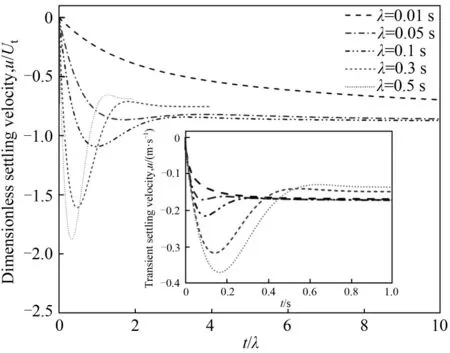
图8 无剪切稀化时松弛时间λ对颗粒沉降瞬时速度的影响Fig.8 The effects of relaxation time λ on transient settling velocity of a particle without shear thinning
除了弹性效应,对剪切稀化对颗粒沉降的影响进行了研究,随着Giesekus 本构方程迁移因子α的增加,剪切稀化效应增强,由图9 可以看出,随着α增加,剪切稀化增强会削弱颗粒沉降速度的波动,当α大于0.3 时,颗粒沉降速度不再出现过冲现象,而是缓慢增加最后达到稳定的终端速度,这是由于剪切稀化效应导致随着颗粒沉降速度增加,颗粒周围剪切速率增大,表观黏度逐渐下降,弹性能量释放后的应力也会减小,因此颗粒会有一个逐渐加速的过程,剪切稀化效应越强,颗粒沉降终速越大。
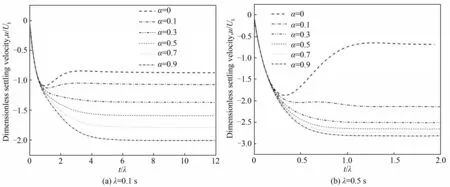
图9 Giesekus流体迁移因子α对颗粒沉降瞬时速度的影响Fig.9 The effects of mobility factor α on transient settling velocity of a particle in Giesekus fluids
对FENE-P 流体,随着伸长率L的增加,剪切稀化效应减弱。由图10 可以看出,拉伸率越小,颗粒沉降速度波动幅度越小,当L=2时,颗粒速度不出现过冲现象,因此弹性应力松弛效应增强颗粒沉降速度的波动,而剪切稀化削弱颗粒沉降速度的波动。

图10 FENE-P流体拉伸率L对颗粒沉降瞬时速度的影响Fig.10 The effects of extensibility L on transient settling velocity of a particle in FENE-P fluids
在实验中观察到颗粒速度的持续拟周期性波动,可以推断颗粒速度波动是由流体的弹性应力松弛效应触发,弹性越强,颗粒沉降波动效应越强,而剪切稀化效应会削弱颗粒的波动,但是采用Giesekus 和FENE-P 本构方程模拟的结果发现颗粒在开始沉降后,速度波动很快消失,达到稳定的终端速度。黏弹性流动的高维森贝格数会引起求解不稳定,容易发散,本文在模拟中发现De超过10 后计算变得难以收敛,使得模拟更强弹性效应的沉降变得困难,可以推断,随着弹性进一步增加,颗粒沉降速度波动周期数和幅度均增加。另一方面,表面活性剂分子形成的蠕虫状胶束溶液由于其流变性质比共价骨架连接的聚合物分子更为复杂,其是一种活性聚合物,胶束之间不断地断裂和重构,其断裂-重构效应会对颗粒运动产生不可忽略的影响,需要从流体中表面活性剂溶液形成的微观胶束结构的动态演变规律去揭示弹性和胶束断裂-重构的相互作用机理。
5.2.2 颗粒沉降负尾迹特性 表面活性剂溶液中颗粒沉降速度的波动可能与颗粒负尾迹有关,因此对颗粒负尾迹特性进行了研究,为了获得颗粒负尾迹的流场特征,将模拟结果转换到惯性参考系,即静止流体中小球的自然下落,结果如图11 所示,可以看出,颗粒在沉降过程中其后缘滞止点(相对于颗粒速度为零的点)附近的流体由于黏性作用随着颗粒向下运动,前缘滞止点附近的流体被颗粒推动向下运动,但是在颗粒两侧表面附近以及向下游延伸的区域里,流体速度反而向上,这是由于此区域的流体受剪切作用较强,由于流体的剪切稀化效应,颗粒周围向下的流体对周围流体的黏滞作用力减小,因此速度最大的区域对外围的影响区域也减小,强剪切带把此区域分成两个部分,就像颗粒带动尾迹区将流体劈开一样。此外,在尾迹区向下游延伸处,出现了一个速度方向与颗粒沉降方向相反的区域,如图11(a)中“负尾迹”所示,这部分流体不断地卷入尾迹区中的流体向上运动,经过一段距离后又被主流携带进入负尾迹旁边的主流区,转而速度向下,在颗粒下游处形成一个循环区域,形成负尾迹区,此处对附近流体的剪切和拉伸会造成大量胶束的断裂和重构,使得流体内部的应力变得不稳定,是造成流场不稳定及颗粒沉降速度波动的根本原因。图11(b)、(c)为沿对称轴的颗粒尾迹区中心线上流体速度分布,纵坐标为速度大小,横坐标为从颗粒后缘滞止点开始的距离,在沉降过程中颗粒表面附近流体由于流体黏滞作用随着颗粒一起向下运动,速度为负,在某些区域出现速度大于零,流体速度与颗粒沉降速度相反,即为负尾迹。由图11(b)可以看出,随着α增大,剪切稀化和拉伸硬化效应增强,负尾迹区增大,并且距离颗粒更远。对Giesekus 流体,当α为0.1 时,负尾迹区反向速度值最大,但是负尾迹向下游延伸较短,随着α逐渐增加至0.7,反向速度值减小,负尾迹向下游延伸加长,随着α继续增加,负尾迹反向速度又逐渐增加。对FENE-P 流体,随着拉伸率减小,剪切稀化增强,反向速度峰值和尾迹区向下延伸长度也是先增大后减小[图11(c)]。
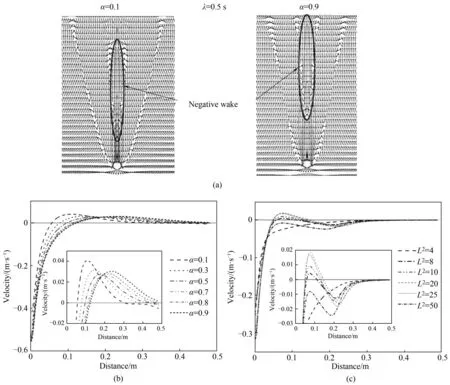
图11 以速度矢量表示的颗粒下游负尾迹(a);Giesekus模型迁移因子α对负尾迹的影响(b);FENE-P模型拉伸率L对负尾迹的影响(c)Fig.11 The negative wake downstream of the particle presented using velocity vector(a);The effects of mobility factor α on negative wake for Giesekus fluids(b);The effects of extensibility L on negative wake for FENE-P fluids(c)
因此,流体剪切稀化和拉伸硬化共同导致颗粒周围流场出现负尾迹,其对颗粒沉降速度不稳定性有着重要作用。
此外,研究了在同样剪切稀化和拉伸硬化时弹性对负尾迹的影响,如图12 所示,可以看出,对于同样的剪切稀化和拉伸硬化(对Giesekus 流体迁移因子α取0.1,对FENE-P 流体伸长率L取5),当松弛时间增加,即弹性效应增强时,颗粒负尾迹反向速度峰值和负尾迹向下游延伸长度都增加,说明了弹性效应越强,负尾迹越强,因此流体的高弹性会强化颗粒负尾迹,其与剪切稀化和拉伸硬化共同导致了颗粒周围流体流动以及颗粒沉降的不稳定,这与剪切稀化和拉伸硬化导致的微观蠕虫状胶束的动态断裂-重构有关,为完全准确描述蠕虫状胶束溶液中颗粒沉降的波动现象,需要进一步探讨适用于微观胶束动态断裂-重构机制的本构模型。
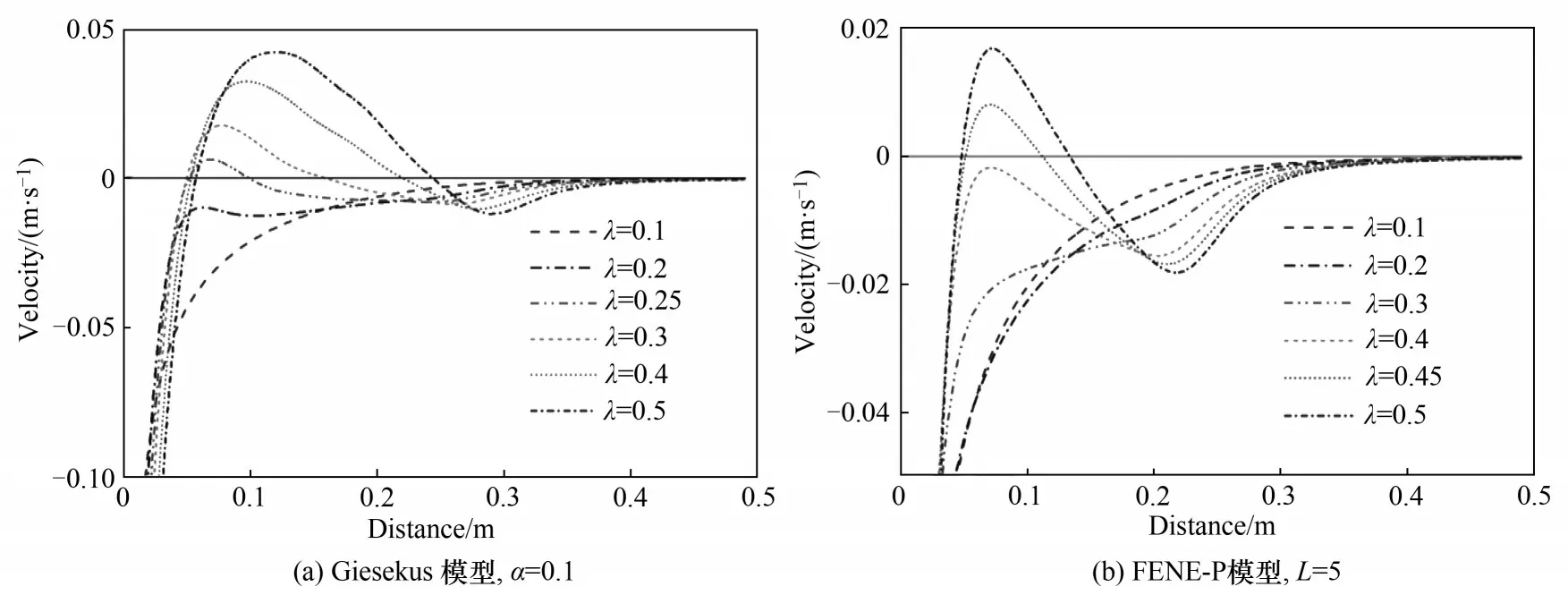
图12 黏弹性对颗粒沉降过程中负尾迹的影响Fig.12 The effects of viscoelasticity on negative wake during the particle settling
6 结 论
本文对黏弹性表面活性剂溶液中球形颗粒沉降特性进行了研究,同时考虑了溶液黏弹性效应和非线性应力应变响应特性,发现颗粒在沉降初期的不稳定性主要是由流体自身的弹性效应引起,弹性效应越强,颗粒沉降速度随时间不稳定性越强,而剪切稀化效应会削弱颗粒沉降速度的波动。
此外发现颗粒在表面活性剂溶液中沉降时在流体剪切稀化和拉伸硬化作用下颗粒下游形成的“负尾迹”,而在纯黏弹性流体无这一现象发生,验证了实验中对蠕虫状表面活性剂溶液中颗粒沉降时负尾迹存在的推测,并且发现剪切稀化和拉伸硬化效应增强会强化负尾迹效应。弹性效应增加时,负尾迹区反向最大速度和向下游延伸长度均增加,负尾迹区与颗粒下沉方向相反的速度分布可能是引起颗粒沉降速度持续波动的原因。
采用Giesekus 和FENE-P 模型虽然可以描述颗粒在经历初始阶段的沉降速度的波动性,但是在解释颗粒连续周期性波动时仍有一定的局限性,这是因为表面活性剂溶液中形成的蠕虫状胶束是一种“活性聚合物”,不同于高分子聚合物溶液,这种流体在剪切拉伸时微观尺度的胶束处于不断地断裂-重构的动态过程,而传统的黏弹性本构模型不能描述在拉伸过程的断裂-重构特性,因此下一步研究应考虑流体中微观胶束的断裂-重构动态过程对于颗粒沉降过程的影响,研究能更好地描述表面活性剂蠕虫状胶束溶液流变性质的本构方程。此外,对于悬浮颗粒体系,颗粒群效应和非球形不规则颗粒均会对颗粒沉降和运移产生重要影响,因此后续应对颗粒群效应和颗粒形状的影响开展研究,获得黏弹性表面活性剂溶液中颗粒沉降的普适规律。
符 号 说 明
a——小球半径,m
D——圆柱通道直径,m
d——小球直径,m
ez——z方向单位矢量
F——惯性力,N
Fg——小球重力,N
Fz——惯性力在方向z的分量,N
fp——黏度系数
fr——松弛函数
G0——弹性模量,Pa
I——单位张量
L——伸长率
n——球表面法向矢量
p——压力,Pa
R——容器半径,m
Re——雷诺数
t——时间,s
Us——颗粒沉降速率,m·s-1
Ut——颗粒斯托克斯沉降速率,m·s-1
u——流体速度矢量,m·s-1
Vs——球形颗粒体积,m3
Wi——维森贝格数
α——迁移因子
γ˙——流体应变率,s-1
λ——松弛时间,s
μP——溶质黏度,Pa·s
μS——溶剂黏度,Pa·s
μ0——零剪切黏度,Pa·s
ρ——流体密度,kg·m-3
ρs——颗粒密度,kg·m-3
τP——黏弹性应力,Pa
