基于POD降阶模型的正弦波翅片扁管管翅式换热器流动与传热特性分析
2022-05-26王烨朱欣悦孙振东
王烨,朱欣悦,孙振东
(1 兰州交通大学环境与市政工程学院,甘肃兰州 730070; 2 铁道车辆热工教育部重点实验室,甘肃兰州 730070)
引 言
随着工业产品的精细化制造和高标准要求,传统的数值设计方法由于面临“海量运算”而难以适应现代工业设计的高效率需求。本征正交分解(POD)技术凭借其降阶求解以及无网格化的优势,已被广泛应用于油气输送[1]、计算机物理通信[2]、废水污染处理[3]、公路运输[4]、绕流流动[5-7]、气液两相流[8]、传 热 传 质[9-10]、湍 流 流 动[11-13]、流 场 分 析 预测[14-17]、翼型流动[18-22]等方面。在换热器流动与传热特性研究方面,丁鹏等[23]首次针对平翅圆管管翅式换热器建立了POD 降阶模型,准确、高效地捕捉到了物理场的详细信息。王烨等[24]通过建立适用于复杂结构的扁管管翅式换热器POD 降阶模型,在计算精度可靠的前提下比有限容积法的计算速度提高了2000 倍。胡文婷[25]采用牛顿插值、拉格朗日插值以及线性插值三种方法建立了适用于求解等壁温边界的扁管管翅式换热器中流动与传热方程的POD 降阶模型,并针对多参数变化情况下不同插值方法所得结果的准确性进行了详细探讨。王烨等[26]采用适体坐标与POD 相结合的方法对比分析了不同边界条件下管翅式换热器的流动与传热性能,为换热器的数值设计中合理设置边界条件提供了理论依据。夏昕彤[27]研究了带三角翼型涡产生器的扁管管翅式换热器,并建立了合适的POD 降阶模型。鲁红钰[28]针对带有不同翼型涡产生器翅片的扁管管翅式换热器建立了分析其流动与传热过程的POD模型,发现采用拉格朗日插值法得到的结果精度最高。王瑞君[29]针对求解复杂结构中流动与传热问题的POD 降阶模型进行了探索,发现POD 方法对于双面带涡产生器的扁管管翅式换热器在耦合热边界条件下有较强的适用性,并极大地提高了仿真速度。但以上采用POD 方法求解管翅式换热器中流动与传热特性的研究主要是针对平翅片展开的,应用POD 技术分析物理结构以及数学描述更为复杂的正弦波翅片扁管管翅式换热器流动与传热特性,还未见报道。本文试图探索能准确求解具有正弦波翅片的扁管管翅式换热器中流动与传热问题的POD 降阶模型,以实现对曲面型翅片换热器的高效数值设计。
1 模型介绍
1.1 物理模型
图1(a)为正弦波翅片[30]扁管管翅式换热器的物理模型。换热器入口处的流体流动方向与水管内流体的流动方向正交,水管交叉对称排列布置。由于换热器模型中空气通道内流场及其模型结构具有周期性和对称性,同时为了提高数值模拟效率,取物理模型中矩形框内的部分为正弦波翅片扁管管翅式换热器计算单元,图1(b)为计算单元的平面示意图。

图1 正弦波翅片扁管管翅式换热器物理模型Fig.1 The physical model of flat tube-bank-fin heat exchanger with sine wave fin
水管布置及正弦波翅片尺寸参数如图2 所示。计算单元结构参数表示符号及数值大小如表1所示。本文所研究翅片类型有平直翅片和4种结构正弦波翅片[由波长(W)为16.43、32.86 mm和波幅(A)为1、2 mm两两组合得到]。扁管管壁热导率λt=398 W/(m·K)[31],材料为铜,管内热水的流动方向沿z轴正向,管内流体为tw=88℃的液态水。翅片材料为镍钢,其热导率λ=13 W/(m·K),相邻翅片间为空气流道,设进口温度为ta=40℃,流动方向沿x轴正向。
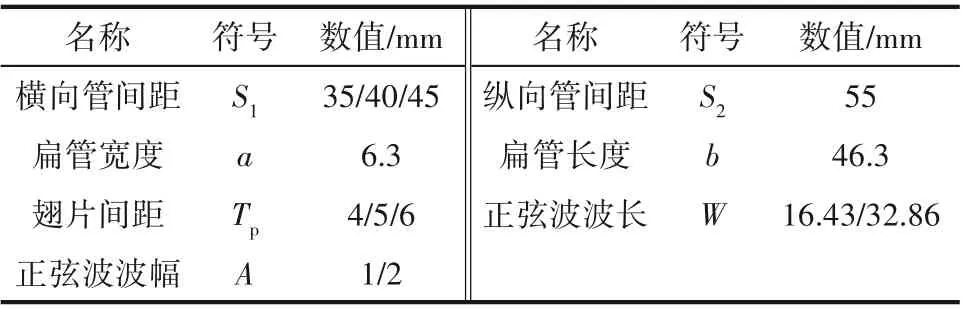
表1 换热单元几何尺寸Table 1 Geometry size of heat exchanger unit
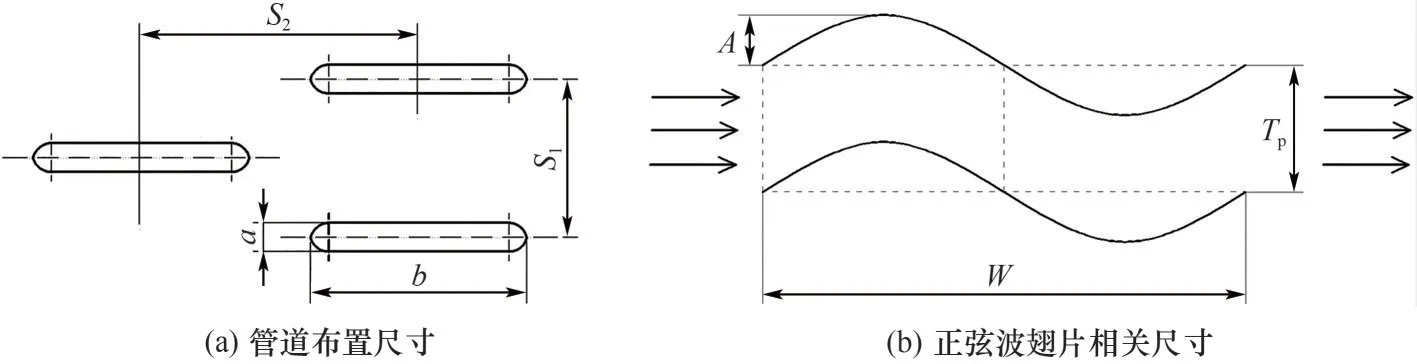
图2 换热器单元及正弦波翅片几何尺寸Fig.2 Geometric dimensions of the heat exchanger unit and sine wave fins
1.2 数学模型
为了多角度对比分析不同类型翅片扁管管翅式换热器流动与传热特性,考虑三维模型进行仿真。结合本文研究背景及目的,在保证计算精度的前提下,做以下假设:流体密度、运动黏度等参数恒定;流体不可压缩;流动为定常;空气的黏性耗散和质量力不予考虑;空气流态为层流。
基于以上假设,控制方程如下。
连续性方程:

动量方程:
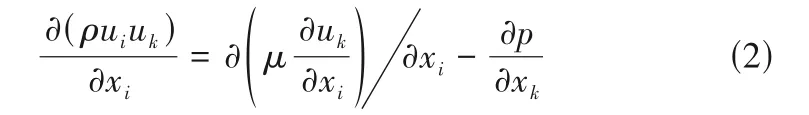
能量方程:

其中,i=1,2,3;k=1,2,3;ρ为密度,常数,kg/m3。其余各参数物理意义见文献[24]。
1.3 边界条件
考虑本文的物理模型尺寸小、翅片厚度薄、翅片材料热导率大等因素,可认为翅片表面温度近似均匀分布。同时,在仿真计算中为了减少计算负荷,忽略壁面厚度。所以,水管管壁以及上、下翅片均采用等壁温边界。换热器计算单元与相邻单元空气侧采用对称边界。空气进口采用速度入口,入口温度为40℃,空气入口雷诺数Rea在400~1300 变化。空气通道出口采用压力出口边界。
2 POD低阶模型的构建
2.1 POD方法基本原理
POD 方法是以实验数据或数值结果为样本,将一般物理问题表示为一组POD 基函数和对应的谱系数线性叠加的低阶形式。所提供的基函数满足最小二乘意义上能量最优条件,将这组基函数和对应谱系数进行线性组合即可实现对高维数据的低维描述。具体实施过程包括:(1)对样本矩阵进行本征正交分解得到POD 基函数;(2)根据物理问题的实际情况,选取含能较高的几组基函数并用插值法计算对应谱系数;(3)将基函数和谱系数进行线性叠加得到原物理场的近似场。与POD 有关的基础理论及公式见文献[32]。
2.2 样本选择
本文POD 样本来源于FVM 计算结果。选取单参数(Rea)、双参数(Rea,Tp)以及三参数(Rea,Tp,S1)同时变化并分别形成6个样本库。样本库中具体参数取值如表2 所示。表中,R={400,500,600,700,800,900,1000,1100,1200,1300},T={4,5,6}(mm),S={35,40,45}(mm)。

表2 样本参数变化Table 2 Sample parameters
2.3 基函数的提取
将2.2 节所得样本导入MATLAB 程序,得到能代表基函数特性的特征值。为了确保所选基函数个数能完全反映物理场信息,需要以此特征值为基础计算累积能量贡献率,从而得到使得该值占总能量99.99%以上的基函数最小个数[27]。根据表2中不同样本矩阵的样本个数,单、双、三参数变化的3 个样本矩阵分别得到10、30、120个基函数。根据累积能量贡献率大小选取的基函数组数如表3 所示,表中结构1 对应(A=1 mm,W=16.43 mm),结构2 对应(A=2 mm,W=32.86 mm)。

表3 基函数组数的选取Table 3 Selection of the basis function numbers
2.4 谱系数计算
通过对比线性插值、牛顿插值、拉格朗日插值三种方法计算温度场和速度场,发现三种插值法计算精度几乎没有差别,但线性插值法速度最快,本文选择线性插值法获得谱系数并重构温度场和速度场。
为了考察POD 降阶模型对正弦波翅片扁管管翅式换热器的适用性,本文充分考虑影响换热器性能的多个变量参数Tp、S1和Rea,通过线性插值方法,在单参数(Rea)、双参数(Rea,Tp)以及三参数(Rea,Tp,S1)变化3 种情形下探讨POD 降阶模型,分析正弦波翅片扁管管翅式换热器流动与传热性能的适用性。
3 数值求解方法
3.1 数学模型验证
本文构建POD 低阶模型的样本来自FVM 计算结果,因此,首先对FVM 计算方法的可靠性进行考核。为此,建立文献[33]的物理模型并采用相同的计算条件,将本文数值结果与其实验测试所得阻力系数f值和努谢尔特数Nu值分别进行对比,如图3所示。可以看出,本文所得参数变化规律与实验结果一致,且相对误差最大值仅为7%,从而验证了本文数值方法的可靠性。
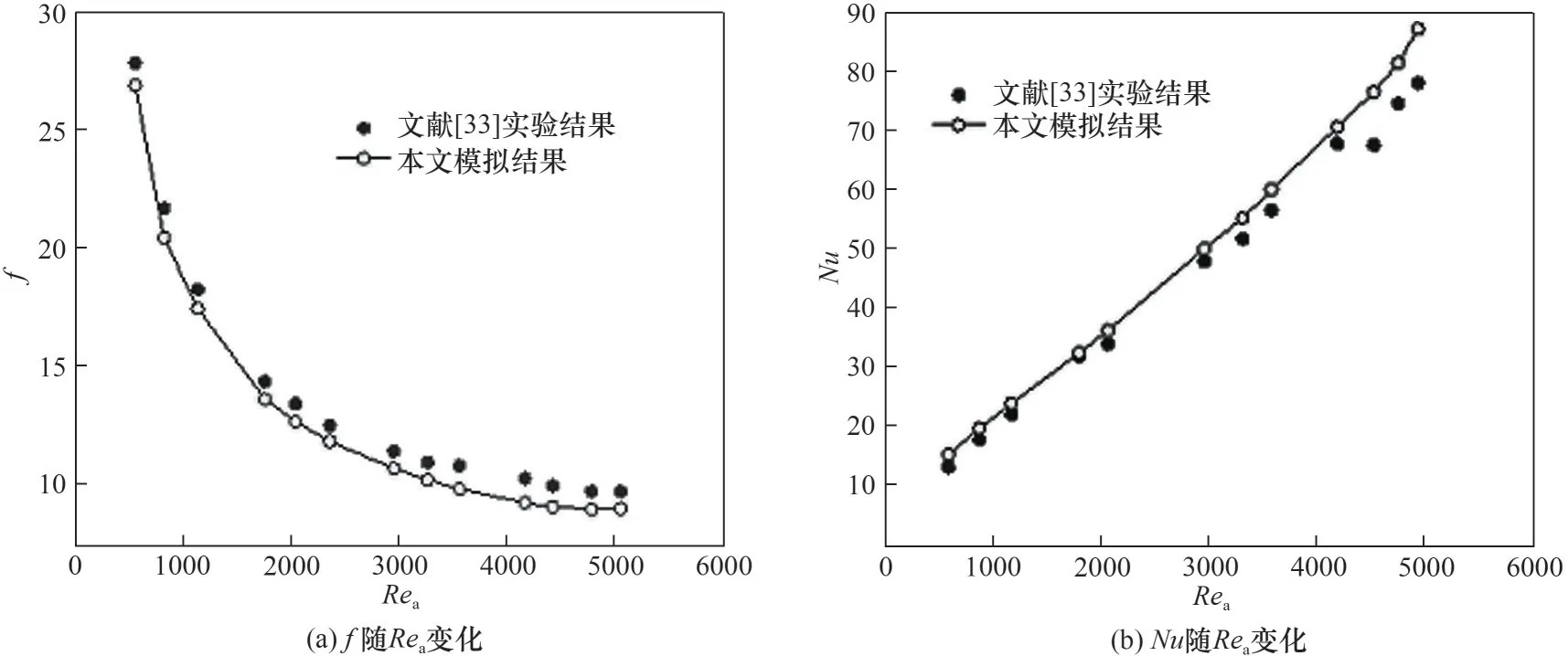
图3 数值方法验证Fig.3 Numerical method verification

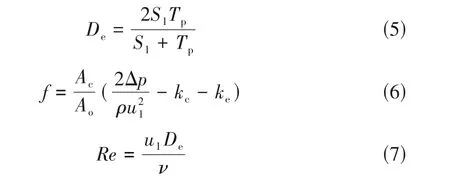
3.2 网格独立性验证
以A=1 mm,W=16.43 mm 结构参数对应工况为例,以空气通道壁面平均努谢尔特数Nu作为考核网格独立性是否满足的指标,计算结果如表4 所示。可以看出,随着网格数的增大,空气通道壁面平均Nu在网格数为359187 时相对网格数为441561 的变化幅度明显低于相对网格数为245628对应工况的变化。因此,对于本文A=1 mm,W=16.43 mm 正弦波翅片换热器,Tp=6 mm,S1=40 mm时,计算采用的网格数为359187。对于其余结构模型的计算网格数采用同样的方法获得。
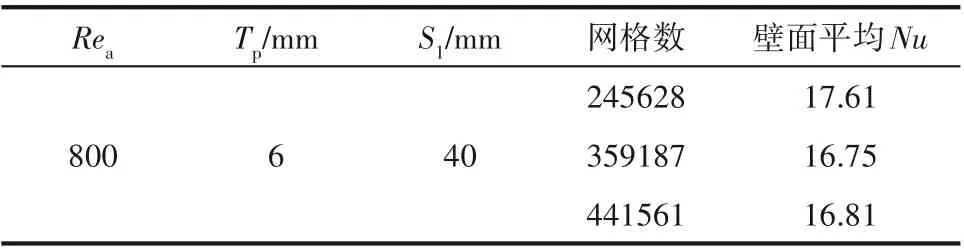
表4 网格独立性验证Table 4 Grid independence verification
4 高阶模型计算结果及分析
4.1 对流传热分析
图4 为S1=40 mm、Tp=6 mm 时不同类型翅片的扁管管翅式换热器空气侧通道壁面平均Nu随Rea的变化关系。由图可见,壁面平均Nu随Rea的增大呈上升趋势,不同结构参数的正弦波翅片换热器的壁面平均Nu均高于平翅片换热器的值,不同结构翅片对应的Nu上升速率存在一定差异。A=2 mm,W=16.43 mm 翅片对应的换热器在所研究的Rea范围内均表现出了较好的传热能力,与平翅片相比,壁面平均Nu平均提高了150.84%。波幅一定,壁面平均Nu随波长的增大而减小;波长一定,壁面平均Nu随波幅的增大而增大。
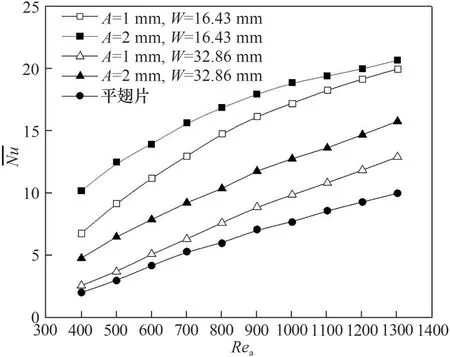
图4 空气通道壁面平均Nu对比(Tp=6 mm,S1=40 mm)Fig.4 Comparison of the average Nu on the wall of the air channel(Tp=6 mm,S1=40 mm)
4.2 流动阻力分析
考察换热器流动阻力及能量损失是其结构设计优化的重要环节。本文主要探讨换热器通道内空气侧的流动特性,对于气体,流动损失通常以压降(ΔP)的形式表示:

式中,Pi,Po分别为换热器单元进口、出口过流断面上的平均压强,Pa。
图5显示了空气侧压降随空气侧雷诺数的变化关系。不同类型翅片换热器的进、出口压降均随空气侧雷诺数的增大呈上升趋势,但上升的速率不同,上升最快的是A=2 mm,W=16.43 mm 翅片换热器,其平均压降接近平翅片的10倍。这是因为雷诺数是一个与气流速度、物性以及过流断面的几何特征有关的无量纲数,雷诺数的增大是这些因素共同作用的结果。层流状态下,气流通道的压强损失主要受雷诺数影响,在本文不考虑气体物性随温度变化的前提下,影响压强损失的因素主要是气流速度和过流断面的几何特征。所以,才表现出了不同翅片参数的换热器中压降随雷诺数的增大其上升速率不同的变化特征。而曲面型翅片结构会导致大量旋涡区的存在以及摩擦损失,从而使其能耗高于平翅片结构。
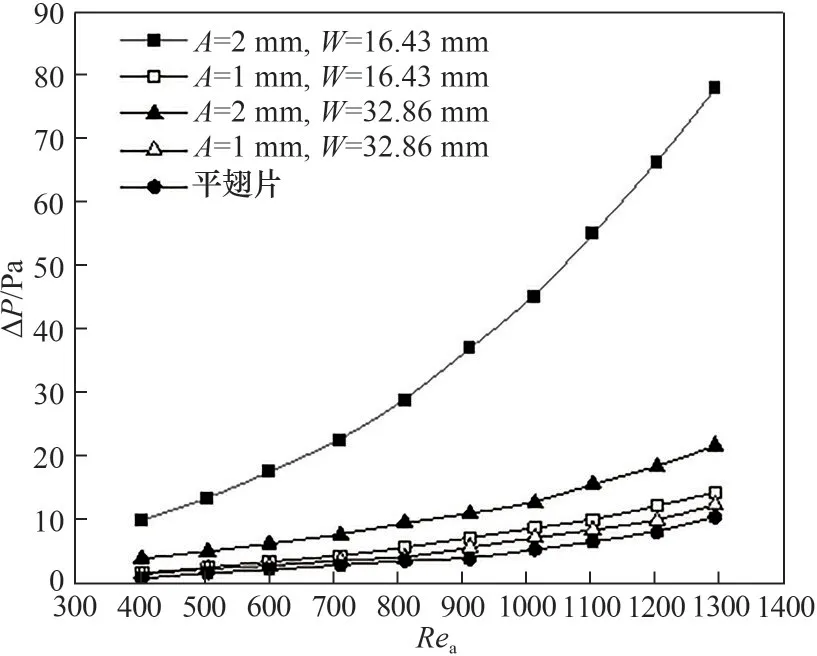
图5 空气侧压降随Rea变化关系Fig.5 The air side pressure drop varies with Rea
4.3 换热器综合性能分析
由上文可知,不同翅片结构在强化传热的同时也会引起不同程度的压强损失。一般采用强化传热JF 因子来评判换热器综合性能的改善程度。强化传热JF因子的计算公式为:

图6为不同类型翅片扁管管翅式换热器强化传热JF 因子随Rea的变化关系。可以看出,A=1 mm,W=16.43 mm 正弦波翅片换热器及A=2 mm,W=32.86 mm 正弦波翅片换热器的强化传热JF 因子均大于1,具有较好的强化传热效果。而A=2 mm,W=16.43 mm 正弦波翅片换热器JF 因子在不同Rea时均小于1,其传热性能弱于平翅片结构。A=1 mm,W=32.86 mm 正弦波翅片换热器在Rea小于900 时,其传热性能弱于平直翅片结构。
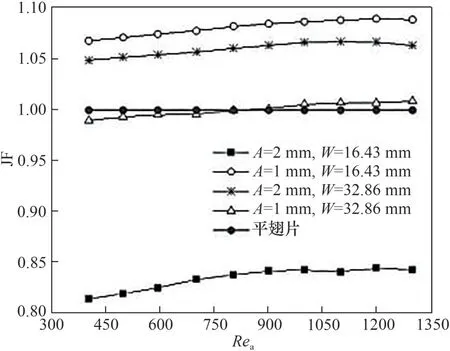
图6 强化传热JF因子随Rea变化关系Fig.6 JF factor of enhanced heat transfer varies with Rea
5 POD降阶模型与FVM结果对比
将高阶模型计算得到的物理场与降阶模型的重构场进行对比,考察POD 降阶模型对正弦波翅片扁管管翅式换热器传热与流动特性的预测精度及适用性。
5.1 单参数变化对比
图7和图8分别为A=1 mm,W=16.43 mm 正弦波翅片扁管管翅式换热器POD 降阶模型重构结果与FVM计算结果在y=S1/2截面上的温度场和速度场对比,图中虚线代表POD 降阶模型重构结果,实线为FVM 计算结果。可以看出,在主流区,POD 降阶模型等值线与FVM 结果吻合得很好。但受波纹翅片扰动的区域,2 种方法所得结果存在一定差异。温度场等值线的重合效果整体优于速度场。
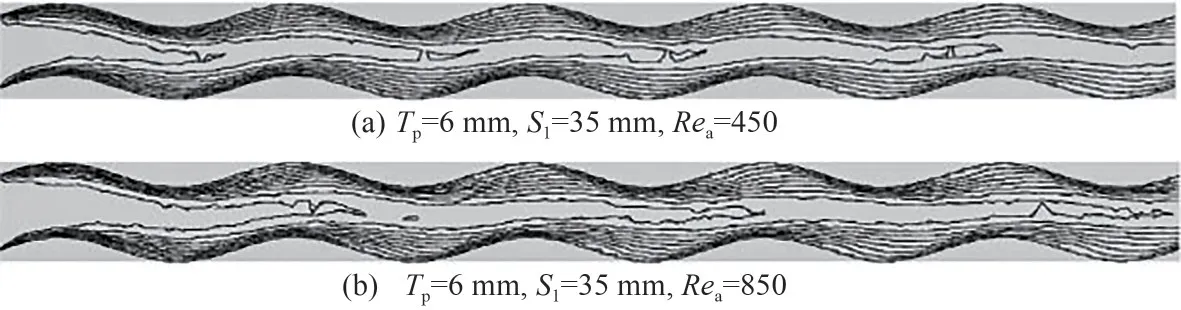
图7 单参数变化时y=S1/2截面温度分布对比(A=1 mm,W=16.43 mm)Fig.7 Comparison of temperature distribution in y=S1/2 section for single parameter(A=1 mm,W=16.43 mm)

图8 单参数变化时y=S1/2截面速度分布对比(A=1 mm,W=16.43 mm)Fig.8 Comparison of velocity distribution in y=S1/2 section for single parameter(A=1 mm,W=16.43 mm)
5.2 双参数变化对比
图9 和图10 为双参数变化下A=1 mm,W=16.43 mm正弦波翅片扁管管翅式换热器采用2种方法所得物理场在y=S1/2截面上的分布对比。与单参数变化类似,在主流区,POD 降阶模型重构场的等值线分布与FVM 结果基本一致,但在受波纹翅片扰动的区域,以及翅片附近的温度分布存在锯齿状等值线。整体来看,双参数变化下2种方法所得温度场等值线吻合较差区域主要集中在第1 管排和第2 管排的主流区域。从单参数和双参数降阶模型的重构结果与FVM 对比结果的共性看出,二者温度场的相对偏差主要存在于翅片表面区域,且沿主流方向呈明显减小的趋势。2 种方法所得速度场等值线的吻合度不如温度场高。
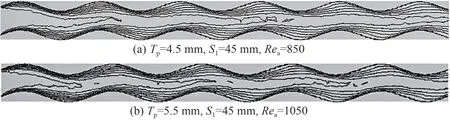
图9 双参数变化时y=S1/2截面温度分布对比(A=1 mm,W=16.43 mm)Fig.9 Comparison of temperature distribution in y=S1/2 section for two parameters(A=1 mm,W=16.43 mm)

图10 双参数变化时y=S1/2截面速度分布对比(A=1 mm,W=16.43 mm)Fig.10 Comparison of velocity distribution in y=S1/2 section for two parameters(A=1 mm,W=16.43 mm)
5.3 三参数变化对比
图11 和图12 为三参数变化下2 种方法所得物理场等值线分布对比。可以看出,三参数变化下温度场和速度场的对比结果与上文分析的单、双参数变化所体现的规律基本一致,温度场差异较小,但位于正弦波翅片附近以及主流区域的速度场等值线分布相对单、双参数变化存在明显差异。这是由于POD 降阶模型的预测精度在样本数量一定的情况下会随着变量的增加而下降[32]。

图11 三参数变化时y=S1/2截面温度分布对比(A=1 mm,W=16.43 mm)Fig.11 Comparison of temperature distribution in y=S1/2 section for three parameters(A=1 mm,W=16.43 mm)

图12 三参数变化时y=S1/2截面速度分布对比(A=1 mm,W=16.43 mm)Fig.12 Comparison of velocity distribution in y=S1/2 section for three parameters(A=1 mm,W=16.43 mm)
5.4 POD降阶模型计算效率分析
以上分析主要从POD 降阶模型预测的局部信息准确性上展开讨论,POD 方法相对传统计算方法的另一个优势体现在计算效率方面。表5为POD降阶模型和FVM 平均计算耗时对比。可以看出,POD降阶模型重构物理场的效率远高于FVM。采用单参数样本插值得到的2种结构翅片扁管管翅式换热器重构场,其计算速度是FVM 的近104倍,双参数和三参数样本插值的计算效率有所下降,但POD 方法耗时仍远低于FVM,极大程度地降低了计算成本。
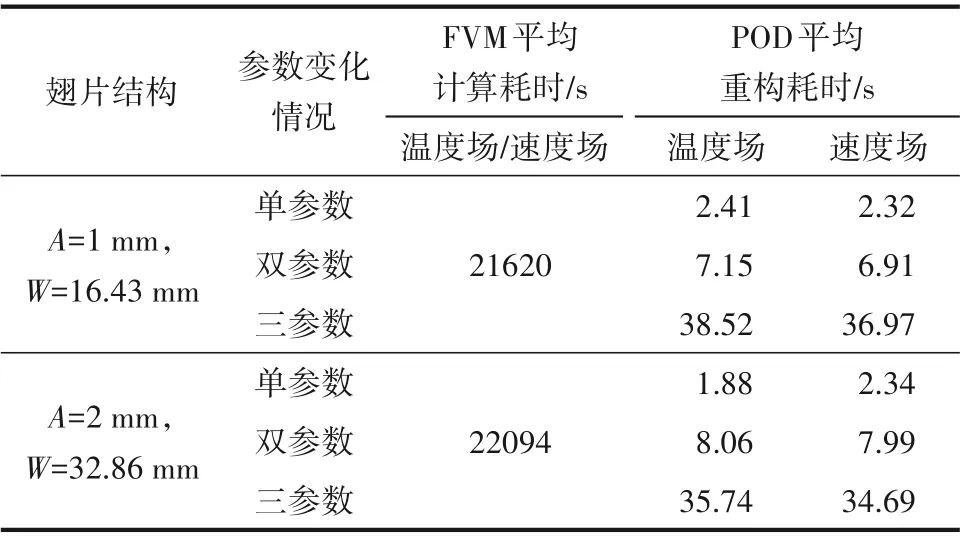
表5 两种方法平均计算耗时对比Table 5 Comparison of average calculation time between the two methods
前期研究表明:三参数变化的POD 降阶模型重构物理场精度稍低于单参数和双参数情况。所以,以三参数为例,对比POD结果与FVM结果间的平均相对偏差。对比表6 和表7 可知,同一翅片结构,对温度场的预测精度要高于速度场,但POD 降阶模型对于速度场的预测平均相对偏差也只有2.921%,说明该模型用于求解曲面型翅片结构换热器中的流动与传热问题具有很好的适应性。
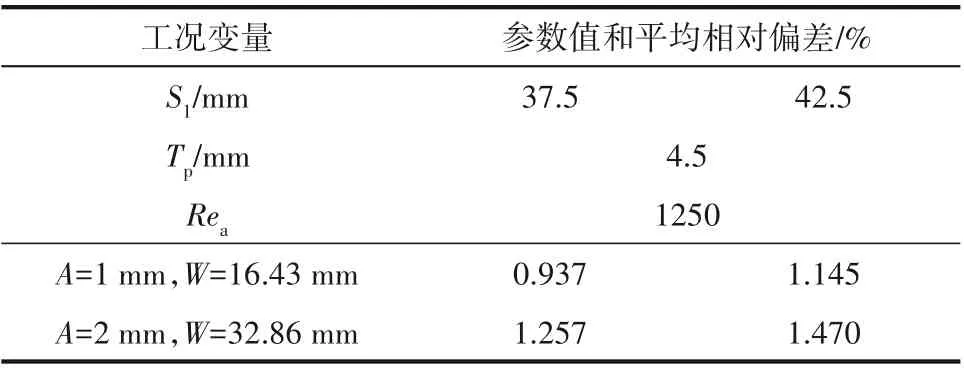
表6 两种方法所得温度场偏差对比(三参数)Table 6 Comparison of temperature field deviation obtained by two methods(three parameters)
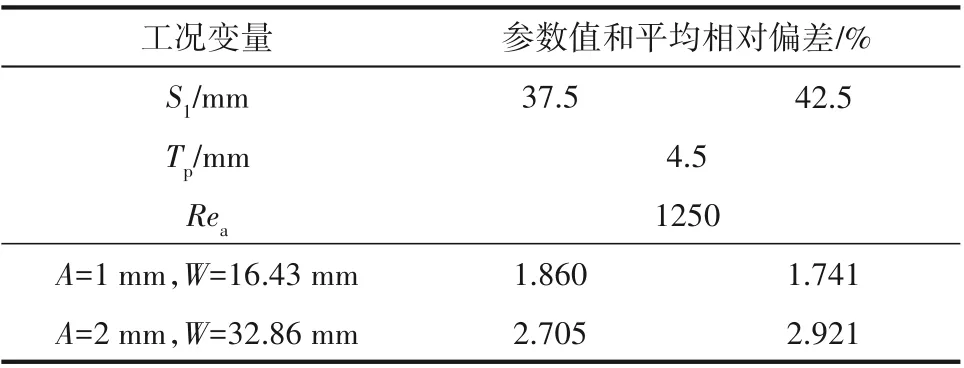
表7 两种方法所得速度场偏差对比(三参数)Table 7 Comparison of velocity field deviation obtained by two methods(three parameters)
6 结 论
本文构建了适用于分析不同结构正弦波翅片扁管管翅式换热器流动与传热特性的POD 降阶模型,旨在探究POD 降阶模型对求解曲面型边界中流动与传热问题的可靠性,并从计算精度、计算效率等方面对其进行验证。得到的主要结论如下:
(1)正弦波翅片相较于平翅片,可以有效提高换热器空气通道内壁面的传热能力,本文所得A=1 mm,W=16.43 mm 正弦波翅片换热器的强化传热效果最优。
(2)POD 重构温度场与FVM 计算结果的吻合度优于速度场,单参数和双参数变化时POD 重构场与FVM 计算结果的相对偏差较三参数低,三参数变化时POD 降阶模型预测的最大平均相对偏差为2.921%。降阶模型对温度场预测的误差主要存在于正弦波翅片表面区域,且沿主流方向呈减小趋势。
(3)从计算效率上看,POD 降阶模型能够大幅降低正弦波翅片扁管管翅式换热器的计算成本。单参数变化时的计算效率是FVM 方法的近104倍,双参数和三参数变化时的计算效率有所下降,但POD方法计算耗时仍远低于FVM。
符 号 说 明
f,fR——分别为正弦波翅片及平翅片阻力系数
h——对流传热系数,W/(m2·K)
Rea——空气侧Reynolds数
S1,S2——分别为横向管间距、纵向管间距,mm
Tp——翅片间距,mm
ta,tw——分别为空气入口温度、管内流体温度,℃
v——运动黏度,m2/s
