(111)取向无铅K0.5Na0.5NbO3 外延薄膜的相变和电卡效应:外应力与错配应变效应*

白刚 韩宇航 高存法

1)(南京邮电大学集成电路科学与工程学院,南京 210026)

2)(南京航空航天大学,机械结构力学及控制国家重点实验室,南京 210016)

无铅 K1–xNaxNbO3 薄膜作为传感器以及机电和电卡冷却装置的候选者越来越受到关注.但是(111)取向K1–xNaxNbO3 薄膜的相变与电卡效应的内在关联还并不清楚.本文首先推导出基于八阶朗道自由能多项式的(111)取向铁电薄膜的热力学势,并在此基础上建立了K0.5Na0.5NbO3 薄膜温度-错配应变相图和室温错配应变-面外应力相图.重点研究了(111)取向K0.5Na0.5NbO3 薄膜的室温电卡效应的应变和取向控制,这对于实际的电卡制冷应用至关重要.研究发现,在无面外应力和零错配应变下,三方铁电-顺电相变附近,30 MV/m电场下K0.5Na0.5NbO3 薄膜在居里温度附近(约673 K)最大电卡绝热温变 ΔT 可高达18 K.施加约–6.7 GPa的面外应力可以有效地将居里温度降低至室温,但代价是最大绝热温变ΔT 降低至7.5 K.本工作为应变和取向工程调控 K1–xNaxNbO3 基薄膜的相变和电卡性能提供了理论指导.

1 引言

近年来,基于固态相变热效应的固态制冷技术被认为是最有希望取代传统气体压缩制冷的技术方案.固态相变热效应主要包括磁卡、电卡、弹卡以及压卡效应.前3 种效应分别源于相应外场对铁性体系中磁矩、铁电极化或应变的有序度的调控,而第4 种效应则常常涉及压力诱导的晶体结构相变[1].相较于磁场,电场构建更简单,成本低廉,且弹卡材料通常容易疲劳.因此,电卡制冷技术具有器件结构简单、易于小型化、操控便捷、成本低廉、环境友好等优点,在可穿戴热管理、芯片热管理、分布式局域热管理、航空航天等领域具有巨大的潜力,被认为是一种非常有发展潜力的高效固态制冷技术[2−8].电卡效应是由电场引起的绝热温度变化或等温熵变化定义.尽管在PbZr0.95Ti0.05O3[1],PbSc0.5Ta0.5O3[7]等许多铁电材料中都观察到了巨大的电卡效应,但它们大多含铅,不能满足环保要求.

无铅铁电体K1–xNaxNbO3(KNN)作为一种非常有前景的替代PbZrxTi1–xO3(PZT)的候选材料,在过去十几年中受到越来越多的关注[8−11].目前,关于KNN 的电卡的研究主要集中在陶瓷上或单晶上[12−14].通常,铁电材料的物理性能包括电卡响应在相变温度附近显著增强[15−20].对于实际的电卡制冷应用,电卡效应的工作温度被期望在室温附近.然而,KNN 块体的居里温度在 650 K 以上[21],远高于室温.有研究表明,静水压力可以有效地将居里温度降低到室温[14,22,23].与块状材料相比,薄膜具有更高的击穿场强,更适用于小型化器件,因此备受关注.然而,施加在薄膜上的双轴面内失配应变通常会升高居里温度[16,24,25].为了降低铁电薄膜的居里温度,显然在薄膜上施加静水压是极不方便且不利于器件小型化,可能需要垂直于薄膜应力来实现.为了产生这种应力,可以通过利用垂直纳米复合材料在垂直于薄膜方向产生平面外错配应变[24,26]或在薄膜表面施加外部应力来实现[25,27].此外,薄膜铁电体的电卡效应研究主要集中在(001)取向薄膜上[28,29].最近本课题组和合作者研究发现由于更加复杂的相变,(111)取向的铁电薄膜具有优越的电卡和介电等性能[30,31].Tagantsev等[32]最早建立了(111)取向的铁电薄膜的唯象热力学理论,但缺乏有效自由能的具体展开式.之后,Ackay 等[33]和 Zhang 等[34]给出了(111)取向的铁电薄膜的有效自由能表达式,但是这些理论,不包括极化的六阶项,因此不能用于对一级相变的研究.Wu 等[35]建立了基于六阶极化项的(111)和(110)取向的铁电薄膜热力学理论,但该理论无法研究朗道自由能包含八阶项的材料,如Ba1–xSrxTiO3,KNN 等.但到目前为止,由于缺乏基于八阶朗道自由能多项式的(111)取向铁电薄膜的热力学势,从热力学的角度深入理解(111)取向铁电薄膜KNN 的相变和电卡性能内在关联仍然缺乏.

本文推导了在垂直薄膜的面外应力和面内等方双轴错配应变共同作用下(111)取向薄膜铁电体 K0.5Na0.5NbO3的热力学势,在此基础上建立了它们的温度-错配应变相图和面外应力-面内错配应变相图,并计算K0.5Na0.5NbO3薄膜的电卡熵变ΔS和温度变化ΔT.研究发现最大电卡ΔS和 ΔT以及相应的工作温度可以通过面内双轴错配应变和面外应力进行调控.例如,在–6.7 GPa 的面外应力和–0.02 的面内双轴失配应变下,(111)取向的K0.5Na0.5NbO3薄膜的最佳工作温度可降至室温,并且在30 MV/m 的外加电场下,对应的最大电卡ΔT约为 7.5 K.

2 热力学理论

虽然Tagantsev 等[32]已经建立了基于六阶朗道自由能多项式函数的(111)取向铁电薄膜的热力学理论,但这个理论具有一定的局限性,它不能被用来研究BaTiO3,KNN,BaxSr1–xTiO3等朗道自由能函数包含八阶项的材料.到目前为止,仍然缺乏包含八阶多项式函数、以及面内双轴错配应变和面外应力的共同作用的(111)取向钙钛矿铁电薄膜的热力学势的表达式,这必然限制了对BaTiO3和KNN 薄膜材料的研究.本文给出了基于八阶多项式函数的(111)取向铁电薄膜的热力学势Gf表达式:

具体细节见补充材料(online).这里,

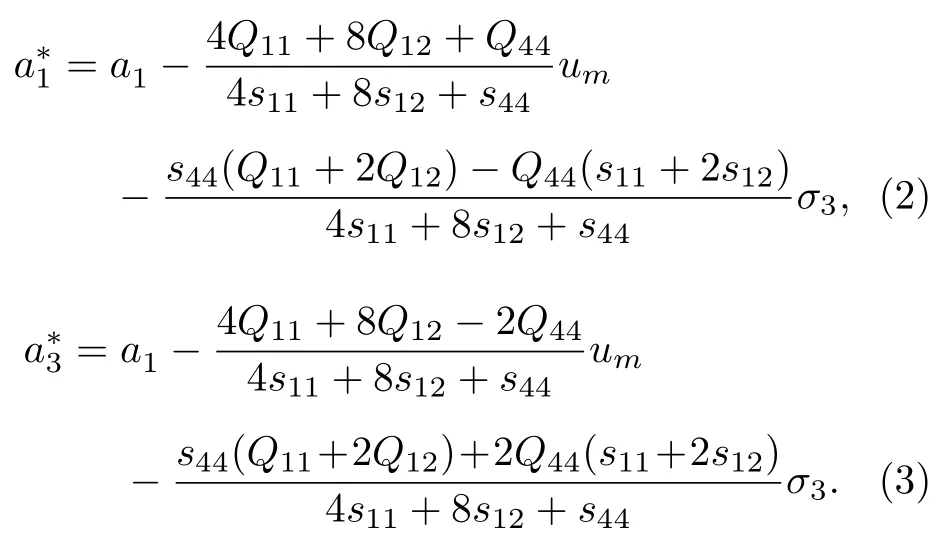
其中Pi和Ei分别是全局坐标系X(X1,X2,X3)下的极化和电场分量,坐标X1,X2,X3分别对应于伪立方晶胞的和 [111].um是面内等方双轴错配应变.σ3是沿垂直于薄膜方向的面外应力.是重整化的介电刚度系数.除了应力部分,(2)和(3)式中的的表达式与 Tagantsev 等[32]获得的表达式相同.其余重整化与温度无关的介电刚度系数见补充材料(online).K0.5Na0.5NbO3的热力学系数从文献[21,36]中获得.在给定的错配应变和面外应力以及给定温度下,平衡极化态可以通过自由能Gf对于极化Pi求极小值获得.

电卡效应可以通过绝热条件下电场引起的温度变化或等温条件下电场引起的熵变化来表征.电场E下的等温熵变化ΔS和绝热温度变化ΔT可以通过下面的(4)式和(5)式评估[37,38]:

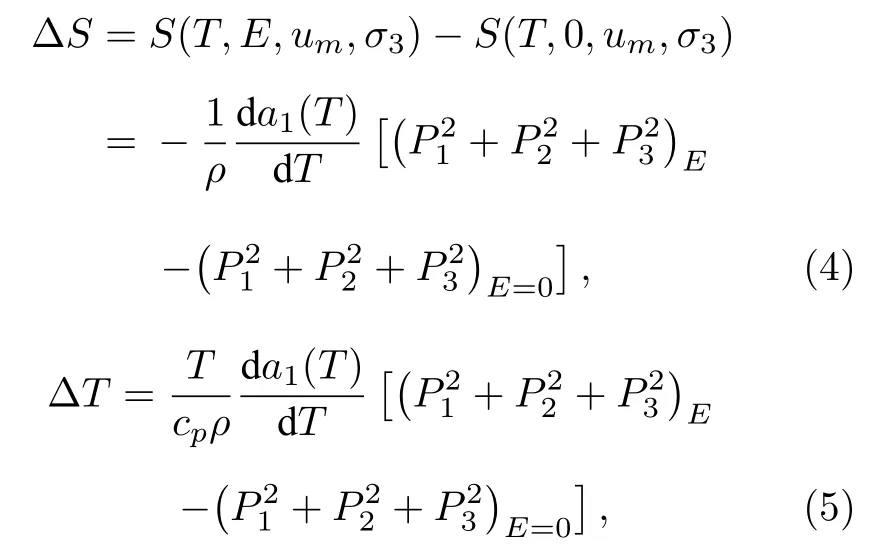
其中,a1是与温度相关的朗道自由能系数,cp是热容,ρ是质量密度.这些材料参数已在补充材料的表S1 (online)中列出.可以看出,电卡 ΔS和ΔT主要由外电场从0 变为E时的极化变化决定,这里的电场变化ΔE=E.

3 结果与讨论

首先计算在没有面外应力的情况下不同温度和等方错配应变下的平衡极化态.在等方双轴应变下,面内应变满足u1=u2=um,u6=0.(111)取向的K0.5Na0.5NbO3薄膜的热力学计算结果如图1及补充材料图 S1 和 图S2 (online)所示.如图1(a)中的失配应变-温度 (um-T) 相图所示,有一个顺电(PE)相和两个铁电单斜(M)和三方 (R)相.它们的极化特性见补充材料表S2 (online).由于机械边界条件的不同,(111)取向的um-T相图与(001)取向K0.5Na0.5NbO3薄膜相图显著不同,在(001)取向相图中,随着压应变到拉应变变化,薄膜能够稳定存在四方(c)、单斜(r)和正交(aa)三个铁电相,但是三方相不能稳定存在[29].对于(111)取向,压应变导致垂直薄膜方向产生拉伸应变,从而导致薄膜面外即[111]方向极化P3增大,因而稳定了三方R 相.拉应变由于诱发了面内极化从而有助于稳定单斜 M 相,其中自发极化被限制在X2-X3平面内.随着温度的升高,极化逐渐减小到零,K0.5Na0.5NbO3薄膜经历从铁电R 相或M 相到顺电PE 相的相变.无论压应变和拉应变,都有助于居里温度的提升.图1(c)—(f) 展示了20 MV/m电场下极化、极化变化、电卡熵变化(ΔS)和电卡温度变化(ΔT) 随应变和温度的变化.如图1(c)所示,沿垂直于薄膜方向即[111]方向施加 20 MV/m的电场后,总极化P增大,极化分布随温度和应变的变化与未加电场(如图1(b))相比有一定程度的变化.电卡ΔS和ΔT在极化变化剧烈的相变附近具有峰值.可以发现,面内压应变比拉应变更容易产生更多的极化变化,进而导致更大的熵和温度变化.在20 MV/m 的电场下,K0.5Na0.5NbO3薄膜在R-PE 相变的居里温度附近具有最大的电卡响应,最大电卡ΔS为–4.2 J/(K·kg),最大电卡ΔT为18.8 K.还注意到,面外压电和介电系数的最大值出现在R-PE 相变附近(见补充材料中的图 S2(online)).而对于(001)取向K0.5Na0.5NbO3薄膜,电卡效应、面外介电和压电性能峰值发生在四方c-立方p 铁电相变和单斜r-正交aa 铁电相变两个相变附近[29].

图1 (111)取向K0.5Na0.5NbO3 薄膜的热力学计算结果 (a) 温度-失配应变相图和(b) 没有外加电场的薄膜极化分布;薄膜在20 MV/m 的电场下的(c)极化分布、(d)极化变化分布、(e)电卡熵变化ΔS 和(f)电卡温度变化ΔT.粗线和细线分别表示一阶和二阶相变Fig.1.Thermodynamic calculated results for (111)-oriented K0.5Na0.5NbO3 films:(a) The temperature-misfit strain phase diagram and (b) the distribution of polarization without electric field;(c) the distribution of polarization,(d) the distribution of polarization change,(e) the electrocaloric (EC) entropy change ΔS,and (f) the EC temperature change ΔT with temperature and misfit strain for (111)-oriented K0.5Na0.5NbO3 films under the electric field of 20 MV/m.Thick and thin lines denote the first-order and secondorder phase transitions,respectively.

图2(a)—(c) 显示了K0.5Na0.5NbO3薄膜在不同面内应变下,电场变化ΔE为20 MV/m 时极化变化ΔP、电卡ΔS和电卡ΔT随温度的变化.对于压应变,随着温度的升高,K0.5Na0.5NbO3薄膜经历从铁电R 相到顺电PE 相的相变,极化变化剧烈,导致ΔS和ΔT的峰值较大.然而,在面内拉伸应变下,K0.5Na0.5NbO3薄膜发生M-PE 铁电相变,极化变化较小,导致ΔS和ΔT的峰值较小.图2(d)—(f)显示了零错配应变、不同电场下ΔP、电卡ΔS和电卡ΔT随温度的变化.由于随着温度的升高,K0.5Na0.5NbO3薄膜会发生M-R-PE 相变(见图1(a)),因此K0.5Na0.5NbO3薄膜在um=0 时的电卡ΔS和电卡ΔT在两个相变附近分别有两个峰值.在零错配应变和20 MV/m 的电场下,RPE 相变温度附近可以获得最大的电卡ΔS和ΔT,分别约为–4.13 J/(K·kg)和 13.5 K;而对于(001)取向的K0.5Na0.5NbO3薄膜,在单斜M-顺电PE 相变温度附近,相同电场下电卡 ΔT只有约3 K[30].

图2 (a)—(c)在ΔE=20 MV/m,不同应变下,(111)取向K0.5Na0.5NbO3 薄膜的极化变化、电卡 ΔS 和电卡ΔT 随温度的变化;(d)—(f)在um=0,不同电场下,(111)取向K0.5Na0.5NbO3 薄膜的极化变化、电卡ΔS 和电卡ΔT 随温度的变化Fig.2.Polarization changes,the EC entropy change ΔS and the EC temperature change ΔT change with temperature for (111)-oriented K0.5Na0.5NbO3 films:(a)–(c) Under different strains at ΔE=20 MV/m;(d)–(f) under different electric fields and strain-free conditions.

室温(298 K)下(111)取向K0.5Na0.5NbO3薄膜的热力学计算结果见图3 以及补充材料图S3(online).图3(a)和图3(b)为(111)取向K0.5Na0.5NbO3薄膜的面外应力-面内配应变(σ3-um)相图,本文计算结果与参考文献[36]中的相图非常一致.这也证明了本文理论的正确性.但是文献[36]并没有给出薄膜的热力学势具体表达式.除了um-T相图中出现3 个相外,正交O 相也被面外压应力诱导出来,并仅在 PE 和 M 相之间稳定.图3(c)—(f)展示了薄膜在 20 MV/m 电场下的极化、极化变化、电卡ΔS和ΔT在相图中的分布.施加电场后总极化P增大,极化分布随应力和应变有一定程度的变化.由于施加的电场,O 和PE 相消失.电卡ΔS和ΔT在极化变化剧烈的R-PE 相变附近具有最大值(图3(d)—(f)).可以发现,当对薄膜施加约6.7 GPa 的面外压应力时,在 0.016 的错配压应变下,居里温度可以降低到室温.

图3 室温下(111)取向K0.5Na0.5NbO3 薄膜的热力学计算结果 (a) 面外应力-面内错配应变相图和(b)没有电场的极化分布;电场20 MV/m 下,(c)极化、(d)极化变化、(e)电卡ΔS 和(f)电卡ΔT 在相图中的分布Fig.3.Thermodynamic calculated results for (111)-oriented K0.5Na0.5NbO3 films:(a) Out-of-plane stress-misfit strain phase diagram and (b) the distribution of polarization without electric field;(c) the distribution of polarization,(d) polarization change,(e) the EC entropy change ΔS,and (f) the EC temperature change ΔT with external stress and misfit strain under the electric field of 20 MV/m at room temperature (298 K).Thick and thin lines denote the first-order and second-order phase transitions,respectively.

图4 显示了室温下不同错配应变下 ΔP、电卡ΔS和 ΔT随面外应力的变化.对于从–0.02 至–0.04 的面内压应变变化,薄膜发生三方R-顺电PE 的铁电相变的临界压应力从约7.3 GPa 上升到约10.8 GPa.显然,由于急剧的极化变化,最大的ΔS和ΔT出现在R-PE 相变附近.此外,ΔS和ΔT的峰值也出现在三相点附近(um=–0.016,σ3=–6.65 GPa)和单斜M-三方R 相变附近(见图3).因此,在um=0 的情况下,ΔS和ΔT分别有两个峰值.图4(d)—(f)显示了在um=–0.02 时不同电场下ΔP、电卡ΔS和ΔT随面外应力的变化.在给定的面外应力和面内错配应变下,极化变化随着施加的电场而增加.电场的应用不仅略微改变了薄膜发生 R-PE 相变的临界应力,且增强了电卡效应.图3(e)和图3(f) 显示了最佳电卡ΔS和ΔT出现在R-PE 相变附近,这是因为在此相变附近极化变化最强烈.在20 MV/m 电场下,由于R-PE相变,电卡ΔS和ΔT在室温下的峰值分别约为–4 J/(K·kg)和6 K.

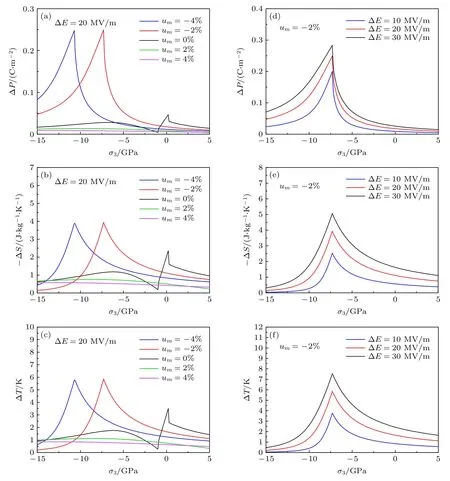
图4 (a)—(c)在ΔE=20 MV/m,不同错配应变下(111)取向K0.5Na0.5NbO3 薄膜的极化变化、电卡ΔS 和电卡ΔT 随面外应力的变化;(d)—(f)在um=–0.02,不同电场下,(111)取向K0.5Na0.5NbO3 薄膜的极化变化、电卡 ΔS 和电卡ΔT 随面外应力的变化Fig.4.Polarization changes,the EC entropy change ΔS and the EC temperature change ΔT change with out-of-plane stress for(111)-oriented K0.5Na0.5NbO3 films:(a)–(c) Under different misfit strains at ΔE=20 MV/m;(d)–(f) under different electric fields and the misfit strain of–0.02.

4 结论

本文首先推导出(111)取向的K0.5Na0.5NbO3薄膜在面内等方错配应变和面外应力共同作用下的热力学势,在此基础上建立错配应变-温度相图和面外应力-错配应变相图.研究发现,垂直薄膜方向的面外应力可以显著降低居里温度并诱导出铁电正交相,这个相在温度-错配应变相图中不存在.此外计算了(111)取向的K0.5Na0.5NbO3薄膜的电卡效应.在无面外应力和零错配应变下,居里温度673 K 附近,30 MV/m 电场下,最大电卡ΔT可高达18 K.约–6.7 GPa 的面外应力可以有效地将居里温度降低至室温,但代价是最大电卡 ΔT降低至7.5 K.本工作提供了对应变工程和取向工程控制薄膜铁电相变和电卡效应的基本理解,并为基于 KNN 的电卡冷却装置的未来设计提供了指导.