玻色-费米超流混合体系中的相互作用调制隧穿动力学*

徐红萍 贺真真 鱼自发 高吉明

(西北师范大学物理与电子工程学院,兰州 730070)

研究了玻色-费米超流混合体系中的相互作用调制隧穿动力学特性,其中玻色子位于对称双势阱中,费米子位于对称双势阱中心的简谐势阱中.采用双模近似方法得到描述双势阱玻色-爱因斯坦凝聚的动力学特性方程组,并将其与简谐势阱中分子玻色-爱因斯坦凝聚的Gross-Pitaevskii 方程进行耦合.通过对不同参数下玻色-费米混合体系中的隧穿现象进行数值研究,发现简谐势阱中费米子与双势阱中玻色子的相互作用使双势阱玻色-爱因斯坦凝聚的隧穿动力学特性更加丰富.不但驱使双势阱中玻色-爱因斯坦凝聚从类约瑟夫森振荡转变为宏观量子自囚禁,而且宏观量子自囚禁表现为三种不同的形式:相位与时间呈负相关并随时间单调减小的自囚禁、相位随时间演化有界的自囚禁以及相位与时间呈正相关并随时间单调增大的自囚禁.

1 引言

20 世纪80 年代以来,量子光学发展了若干种方法:冷原子云释放再捕获(release and recapture,RR)[1]、冷原子云受迫振荡[2]、冷原子光谱分析[3]、非平衡四波混频[4]、飞行时间光谱(time of flight,TOF)[5]和二维飞行时间吸收成像[6]等.目前,实验上不仅实现了稀薄超冷原子气体的玻色-爱因斯坦凝聚(Bose-Einstein condensate,BEC)[1],还实现了双组份超冷玻色-费米混合气体的量子简并,如:7Li-6Li[2],41K-40K[3],23Na-6Li[4],87Rb-6Li[5]和87Rb-40K[6]体系.超冷多体量子简并气体促进了当前原子分子物理、凝聚态物理、光学物理和量子信息等领域的研究.超冷原子气体在实验上的可控性(如利用Feshbach 共振技术,通过调节外部磁场来改变原子间相互作用,以及操控光晶格外势对系统进行周期调制,改变原子在不同格点的占据数和跃迁等)吸引研究者对该体系中的动力学特性展开了大量研究.在理论上,人们在对超冷双组份混合气体的研究中发现了一系列奇特的现象:约瑟夫森振荡、隧穿现象、涡旋[7]、对称性破缺[8]、孤子[9]、超固体[10]、超流体[11,12]、安德森局域化[13]、量子液滴[14]等.

宏观量子隧穿显示了量子多体波函数的聚集隧穿行为,在各种系统中都被研究过.两个弱耦合BEC 之间的量子隧穿包括约瑟夫森振荡、非线性朗道-齐纳隧穿[15]、Rosen-Zener 隧穿[16]等.特别地,随着时间的演化,在对称双势阱中的BEC 的大多数粒子局域在一个势阱中,表现出高度不对称的宏观量子自囚禁现象(macroscopic quantum self-trapping,MQST)[17].量子隧穿现象中很多参数在实验上可以被直接调节,如:基态能量差、隧穿系数、粒子数等,因此超冷原子气体背景下的宏观量子隧穿现象的研究受到了广泛关注.光晶格中费米超流气体约瑟夫森振荡现象的研究为探究整个Bardeen-Cooper-Schrieffer (BCS)超流端到BEC 端渡越区中的费米超流体提供了难得的机会.在实验方面,研究者们在光晶格中观察、研究了玻色-费米混合体系的输运现象.但是,在不同势阱中具有种间、种内相互作用的玻色-费米混合体系的动力学研究很少受到关注.

本文利用双模近似研究了玻色-费米超流混合物中的相互作用调制隧穿动力学,其中对称双势阱中玻色子的隧穿性质受到位于双势阱中心的简谐势中的费米子相互作用的调制.首先利用双模近似求解耦合含时Gross-Pitaevskii (GP)方程,得到系统的动力学方程组,在不同的参数下绘制了0-模和 π-模下的动力学相图,并对这些相图进行了分析.发现简谐势阱中费米子与双势阱玻色子的相互作用,丰富了双势阱BEC 的隧穿动力学特性.不但通过改变不同的初始参数使双势阱BEC 从类约瑟夫森振荡转变为MQST,而且发现MQST 表现为三种不同的形式.

2 物理模型

基于玻色-费米混合体系的实验和理论研究,探究了玻色-费米超流混合体系的隧穿动力学.其中弱排斥相互作用的玻色原子气体囚禁于双势阱中,在双势阱中心位置处对称放置的简谐势阱中囚禁了粒子数相等的双组份费米气体.当体系的温度足够低时,对于粒子数足够多且处于同一量子态的玻色原子,可以用GP 方程来描述其动力学特性.对于简谐势阱中的费米气体,利用Feshbach共振技术调节费米原子间的相互作用可以实现从BCS 超流端渡越到BEC 端.此时,贋自旋方向向上和向下的两个费米原子构成了弱相互作用的两体束缚态.远离幺正区域时,处于BEC 端的费米气体可以看作弱相互作用的分子BEC,因此BEC端的费米气体也可以用GP 方程来描述.这里仅探究一维的情况,耦合含时玻色-费米超流混合物在零温时可以用如下GP 方程来表述[18−20]:

其中,ψb(x,t)和ψf(x,t)分别为玻色子和费米子的序参量,满足=Nb,f,Nb,Nf分别为玻色子和费米子的原子数;mf为费米子的质量;玻色子的质量mb=2mf;参照文献[15],取双势阱VD=(1/2)mω2x2+,简谐势阱VH=(1/2)×mω2x2,d为双势阱的势垒高度,ω为简谐势的捕获频率,σ为高斯势垒宽度;gb=为玻色-玻色种内相互作用系数,gf=为费米-费米种内相互作用系数,gbf=为玻色-费米种间相互作用系数,mR=mbmf/(mb+mf)为约化质量,abb,aff和abf分别为玻色-玻色散射长度、费米-费米散射长度和玻色-费米间散射长度.取简谐振荡的无量纲单位=mf=ω=1 .

双模近似方法在研究双势阱中BEC 的动力学特性时被广泛使用[21−23].在弱耦合极限下,采用双模近似,双势阱中玻色原子凝聚体的序参量ψb(x,t)可以写为

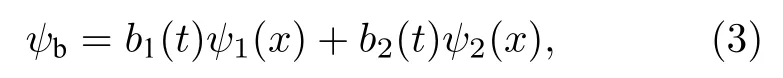
将方程(3)代入到方程(1)中,在方程两边分别乘以ψ1(x)和ψ2(x),然后在全空间积分,利用正交归一条件,可以得到b1,2(t),θ1,2(t)所满足的动力学方程:

其中,

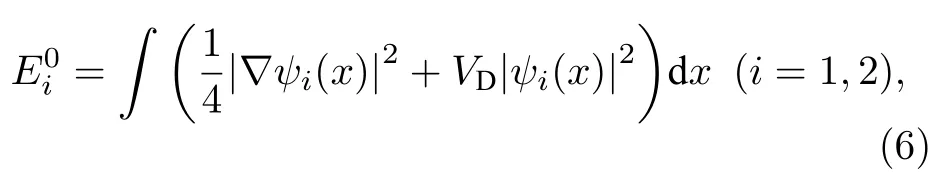
通过把b1,2(t)的表达式代入到(4)式和(5)式,分离虚部和实部,再把方程(3)代入到方程(2)中,可以得到玻色-费米超流混合体系最终的演化方程:

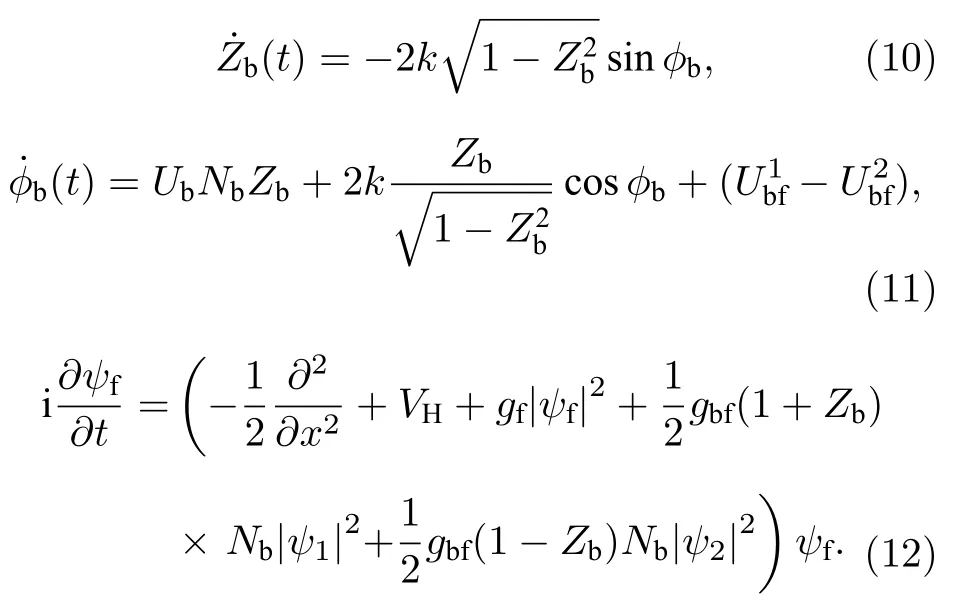
3 数值模拟

目前,各研究小组已经研究了双组份BEC 在双势阱中的玻色-玻色隧穿动力学[24,25]、费米-费米隧穿动力学[26]及玻色-费米隧穿动力学[27].研究结果表明,玻色-爱因斯坦凝聚的隧穿动力学大致可以分为3 种模式:1)0 相位振荡模式(0-模),即粒子布居数差在一个周期内的平均值〈Zb(t)〉=0,相位平均值〈φb(t)〉=0 的振荡模式;2) π 相位振荡模式(π-模),即粒子布居数差在一个周期内的平均值〈Zb(t)〉=0,相位平均值〈φb(t)〉=π 的振荡模式;3) MQST 模式,即粒子布居数差在一个周期内的平均值〈Zb(t)〉≠0 ,相位平均值可以为正负、零或π的振荡模式.下面对以上3 种模式进行详细讨论.

1) 双势阱中的初始粒子数Nb对0-模的影响

当Nb=0.3Nf时,玻色原子数较小,原子间相互作用较弱,原子可以自由地在两个势阱中来回隧穿.双势阱中玻色子的粒子布居数差随时间的变化表现为正弦振荡,相位随时间的变化是有界的,Zb-φb相图表现为一个封闭的圆圈,这种振荡模式被称为类约瑟夫森振荡,如图1(a)所示.当Nb=Nf时,随着玻色原子数增加,原子间排斥相互作用增强,粒子隧穿效应受到抑制,进而局域在双势阱的某一侧,体系进入了自囚禁状态,具体表现为〈Zb(t)〉Zb(0),相位随时间演化是有界的,此时Zb-φb相图是封闭的,称这种囚禁模式为MQST2模式,如图1(d)所示.当Nb=7Nf时,体系仍然处于自囚禁状态〈Zb(t)〉>Zb(0),此时相位与时间呈正相关,并随时间单调增大,此时Zb-φb相图不再封闭,称此囚禁模式为MQST3模式,如图1(e)所示.

图1 0-模时双势阱玻色子初始粒子布居数差 Zb(t)和相对相位 φb(t)随时间 t 的变化关系,以及 Zb-φb相图 (a)Nb=0.3Nf;(b)Nb=Nf;(c) Nb=2.2Nf;(d)Nb=5.5Nf;(e)Nb=7Nf.(a)—(e)图中的初始条件为 Zb(0)=0.6,φb(0)=0,Nf=260,gb=2×10−4,gf=2×10−4,gbf=2×10−2Fig.1.For zero mode,population imbalance change with time t,phase change with t and population imbalance change with the phase of the double-well:(a)Nb=0.3Nf;(b) Nb=Nf;(c) Nb=2.2Nf;(d)Nb=5.5Nf;(e)Nb=7Nf.For (a)–(e) figures the initial condition is set to Zb(0)=0.6,φb(0)=0 ,Nf=260,gb=2×10−4 ,gf=2×10−4 ,gbf=2×10−2 .

2) 双势阱中初始粒子数Nb对 π-模的影响

如图2 所示,双势阱中玻色子的振荡开始表现为类约瑟夫森振荡,随玻色原子数的增加依次由MQST2模式转变为MQST1模式再回到类约瑟夫森振荡,最后进入MQST3模式.然而0-模时体系开始表现为类约瑟夫森振荡,之后随着玻色原子数的增加,经历由MQST1模式到类约瑟夫森振荡再到MQST2模式的转变,最后进入MQST3模式,其中MQST1模式时〈Zb(t)〉Zb(0).而对于 π-模,MQST1模式时〈Zb(t)〉>Zb(0),MQST3模式时〈Zb(t)〉

4 相图和相变分析

已经分析了当费米粒子数不变,0-模和 π-模时双势阱中玻色粒子数目对双势阱中BEC 隧穿动力学的影响.接下来,当费米粒子数目Nf=300 时,改变玻色粒子布居数差,得到了Zb-φb平面内的相图,如图3 所示.当Nb=10 时,体系在0-模及 π-模时只存在类约瑟夫森振荡,如图3(a)所示.当Nb=30时,体系存在3 种振荡模式:0-模时,当Zb(0)较小时,体系处于类约瑟夫森振荡;随Zb(0)的增大,体系由类约瑟夫森振荡向MQST1模式转变,转变的临界值为Zb(0)=0.92.π-模时,当Zb(0)较小时,体系处于MQST2模式;随着Zb(0) 的增大,体系由MQST2模式向类约瑟夫森振荡转变,转变的临界值为Zb(0)=0.87,如图3(b)所示.当Nb=300时,0-模时与图3(b)的演化过程相同,但是体系由类约瑟夫森振荡向MQST1转变的临界值Zb(0)为0.58; π-模时,体系只存在自囚禁模式,体系由MQST1向MQST2模式转变的临界值Zb(0)为0.8,如图3(c)所示.当Nb=600 时,0-模时体系由类约瑟夫森振荡向MQST1转变的临界值Zb(0)为0.65; π-模时与图3(b)和图3(c)的演化不同,体系一开始处于类约瑟夫森振荡,当Zb(0) 增大到0.83 时,体系向MQST3模式转变,如图3(d)所示.当Nb=1800 时,0-模时体系只存在自囚禁模式,体系由MQST3向MQST2模式转变的临界值Zb(0)为0.51; π-模时与图3(d)的演化过程相同,但是体系由类约瑟夫森振荡向MQST3转变的临界值为0.27,如图3(e)所示.进一步增加玻色粒子数目,当Nb=2100 时,体系又重复图3(e)的过程,如图3(f)所示.

由图3 的相图可以看到,0-模时,随玻色粒子数增加,体系由类约瑟夫森振荡向MQST1模式转变的临界值先减小后增大,最后仅存在自囚禁相.由此说明玻色粒子数增加抑制了双势阱中BEC的隧穿效应.同时,简谐势阱中的费米原子丰富了双势阱BEC 动力学,使其出现了3 种不同特征的MQST 模式.而 π-模时情况较复杂,玻色粒子数较小时,体系由MQST2模式向类约瑟夫森振荡转变;增大玻色粒子数,体系只存在自囚禁模式;进一步增大玻色粒子数,体系由类约瑟夫森振荡向MQST3模式转变,转变的临界值随玻色粒子数增加而减小.

简谐势阱中费米子对双势阱中玻色子的调制与二者之间的相互作用能有关,然而粒子数比值Nb/Nf和相互作用强度gb,gf,gbf都会影响二者之间的耦合强度,进而共同调制双势阱BEC 的隧穿动力学.图4 展示了双势阱BEC 在粒子数比值Nb/Nf和相互作用强度gb,gbf下的相图.除了前面讨论的增加Nb可以使双势阱BEC 由类约瑟夫森振荡向自囚禁转变外,从图4 可以得出,固定Nb/Nf之值,增大gb和gbf的值也能使体系产生由类约瑟夫森振荡向自囚禁相的转变.

图4 (a),(c)0-模和(b),(d)π-模时,Nb/Nf-gb 和Nb/Nf-gbf 平面内的相图,其中(a),(b)参数为 gf=2×10−4,gbf=2×10−2;(c),(d)参数为 gb=2×10−4,gf=2×10−4Fig.4.For (a),(c) zero mode and (b),(d) π mode,the phase diagram in the Nb/Nf-gb and Nb/Nf-gbf plane with (a),(b)gf=2×10−4,gbf=2×10−2 and (c),(d) gb=2×10−4,gf=2×10−4.

5 结论

本文研究了玻色-费米超流混合物的隧穿动力学特性,其中玻色子位于双势阱中,费米子位于双势阱中心的简谐势阱中.利用双模近似方法得到描述双势阱BEC 的动力学特性方程组,并将其与描述简谐势阱中分子BEC 的GP 方程进行耦合,通过数值模拟讨论了玻色-费米超流混合物相互作用调制的隧穿动力学特性.研究发现,通过改变体系的初始参数,如玻色粒子数、费米粒子数、玻色子间相互作用强度、费米子间相互作用强度、玻色-费米间相互作用强度以及粒子布居数差和相对相位,都能使双势阱中的BEC 由类约瑟夫森振荡向自囚禁模式转变.0-模时随着玻色原子数的增加,体系依次经历了以下变化:类约瑟夫森振荡→相位随时间单调减小并始终小于零的自囚禁(MQST1)→类约瑟夫森振荡→相位随时间在有界范围内变化的自囚禁(MQST2)→相位随时间单调增大并始终大于零的自囚禁(MQST3). π-模时随着玻色原子数的增加,体系依次经历了以下变化:类约瑟夫森振荡→相位有界的自囚禁(MQST2)→相位随时间单调减小并始终小于零的自囚禁(MQST1)→类约瑟夫森振荡→相位随时间单调增大并始终大于零的自囚禁(MQST3).以上变化过程与双势阱中BEC 的隧穿特性显著不同.由此可以得出,位于双势阱中心简谐势阱中的费米子与双势阱中玻色子之间的相互作用丰富了双势阱BEC 的隧穿动力学特性.