大型混流泵站流道优化与模型试验

杨平辉，李彦军，彭玉成

（1.武汉特种工业泵厂有限公司，武汉 430058；2.江苏大学国家水泵及系统工程技术研究中心，江苏镇江 212013；3.华中科技大学 能源与动力工程学院，武汉 430074）

0 引言

混流泵的比转数范围介于离心泵和轴流泵之间，兼有离心泵高效区范围宽广和轴流泵大流量的优点，因此在国民经济各个领域得到了越来越多的应用。随着城市建设的发展，城市排涝防洪工程建设得到了越来越多的重视，大型排涝泵站建设的越来越多。由于在不同的季节和时期降雨量和城市内外河水位变化较大，排涝泵站的实际运行净扬程在不同的时期变化范围较大。由于混流泵自身所具有的高效区范围广和流量大的优点，在大型排涝泵站中得到了越来越多的应用。

大型混流泵站一般均为立式泵站，采用的流道一般为肘形进水-虹吸出水、肘形进水-直管出水的型式［1］。肘形进水流道在大型泵站中应用较多，水力性能较好［2］。虹吸出水流道的特点是断流方式简单，管理方便，运行安全可靠，流道断面形状变化复杂，土建工程量较大，起动扬程较高，且对出水水位变化幅度有一定的要求。直管式出水流道的特点是结构简单，施工方便，起动扬程低，运行较稳定，需要增设拍门或快速闸门等断流设施［3］。虹吸出水流道和直管式出水流道在大型泵站中均得到了较为广泛的应用，设计方法也已成熟［4-9］。

大型排涝泵站的外河水位变化幅度较大，最高水位较高而最低水位又较低时，采用虹吸式出水流道满足不了驼峰顶部真空度的要求，采用直管式出水流道出口又不能淹没在最低水位以下，此时，就需要采用低驼峰式（又称为屈膝式）出水流道。低驼峰式出水流道是在直管式出水流道管线下倾的基础上演变而来，为了适应水流的变化趋势，低驼峰式出水流道的型线通常采用曲线形式。对于低驼峰式出水流道，出水弯管转弯角度大，型线较为复杂，设计不好则会导致水力损失较大，装置效率低下，运行不稳定等不良后果［10］。

目前对大型混流泵站低驼峰出水流道的研究较少，优化设计方法不够成熟，需要进一步研究。以下以樊口二站为工程背景，对低驼峰出水流道的混流泵装置进行优化和模型泵装置试验研究，为同类型泵站提供参考。

1 工程概况

樊口二站位于湖北省鄂州市樊口镇粑铺大堤上，泵站位于樊口电排站左侧，与樊口电排站共同承担梁子湖排涝任务，泵站设计流量150 m3/s。装机容量为5×4 000 kW。装设5台立式全调节混流泵，配套电动机为10 kV TL4000-40/4250 型同步电机。泵站采用肘形进水流道，低驼峰式出水流道的装置形式，叶轮直径D=2.9 m，转速n=150 r/min。泵站的纵剖面布置如图1所示，泵站的运行特征扬程见表1。

图1 泵站纵剖面布置Fig.1 Vertical section layout of pumping station

表1 泵站运行特征扬程Tab.1 Operating characteristic heads of pumping station m

由表1可知，泵站的运行扬程变化范围非常大，对水泵模型和装置型式的选择与优化设计带来很大难度。

2 肘形进水流道优化分析

进出水流道的所有曲线，均用有理Bezier曲线描述。肘形进水流道的几何形状复杂，完全确定它的几何模型，需要较多参数。不同的参数对应不同的进水流道，从而对应不同的水力性能。影响肘形进水流道水力性能主要是弯管处的型线参数，因此主要对肘形弯管的型线进行优化。首先对肘形进水流道进行参数化三维造型，然后应用CFD仿真技术进行三维流场数值仿真寻优，最终确定出最优的流道型线方案。

进水流道优化主要满足以下2个目标：

（1）流动损失最小。

流动损失可以通过计算进水流道吸入口的总压与进水流道出口的总压差来衡量，通过调整进水流道弯肘部分的形状来达到最优。

（2）进水流道的出口速度均匀度最优。

采用进水流道出口速度标准差衡量，由下式计算：

φf是出口截面上某个单元上的速度是按面积平均的速度，Af是某个单元面的面积。显然理想状况下δ=0表示该截面上所有的速度都相等，在优化过程中δ 越小越好。

三维参数化造型软件通过运行宏脚本文件，即可自动生成适于CFD仿真的计算域实体模型。为了更加真实反应实际边界条件，进水流道向外延伸成圆柱面。将三维造型软件生成的计算域实体模型读入到CFD仿真平台中，一方面自动生成计算域网格，另一方面自动设置进水流道的流场求解策略，然后进行计算和后处理。流体动力学方程采用RANS，即雷诺平均的纳维·斯托克斯方程，具体是采用SST k-ω湍流方程。

在设计流量30 m3/s工况下，调整弯肘的形状，保持其它参数不变，总共进行了5个方案的优化比选，每个方案的流动损失和出口速度标准差见表2。

表2 进水流道优化方案及性能对比Tab.2 Comparison of optimization schemes and performance of inlet channel

由表2可知，方案3是最优方案，图2为方案3的内部流场分布。由图2可以看出，进水流道内无流动分离情况，流速均匀变化，出口流速分布均匀度较好，可以满足水泵高效安全稳定运行的进水要求。

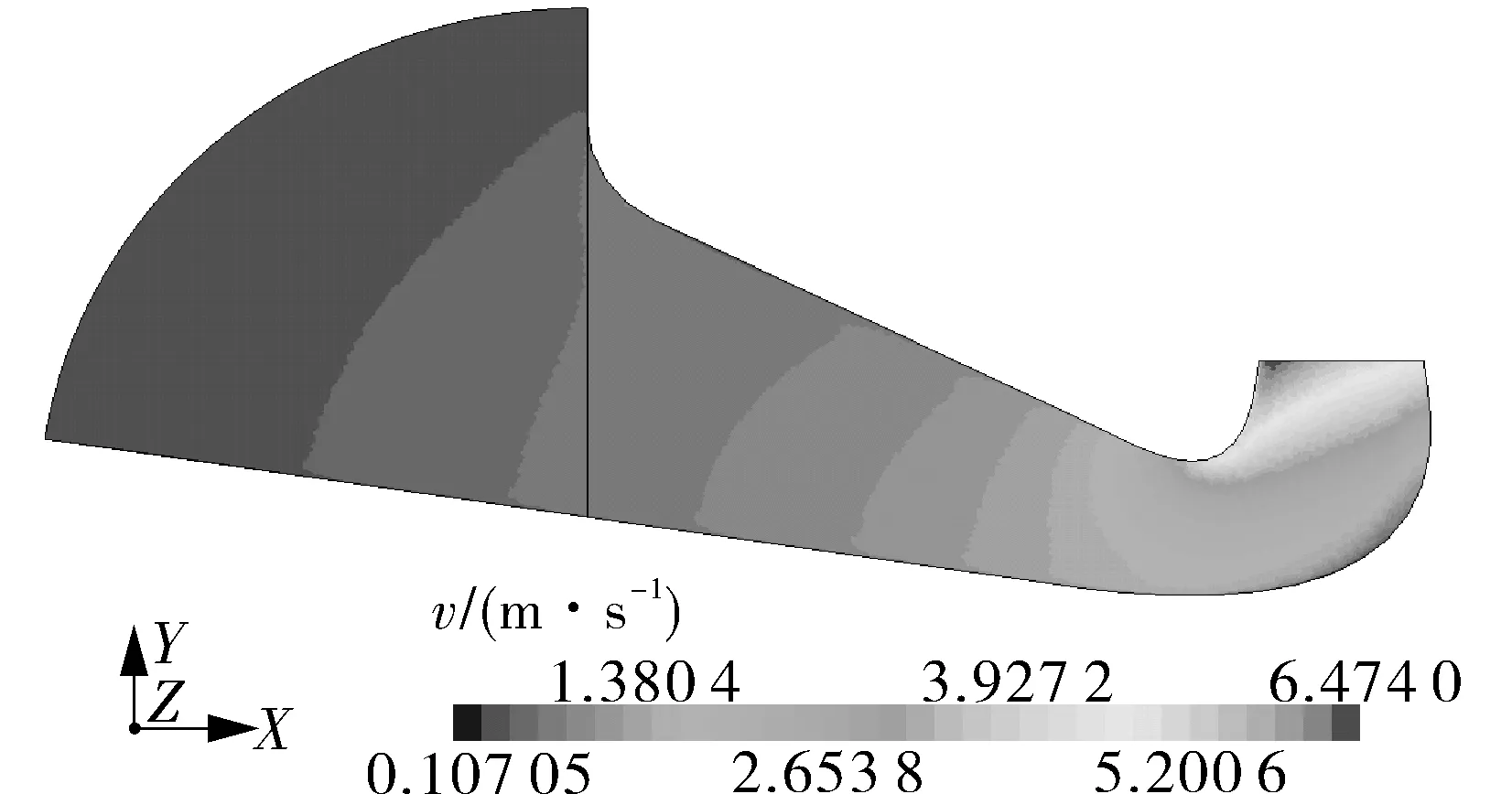
图2 方案3内部流场分布Fig.2 Internal flow field distribution of Scheme 3

3 低驼峰出水流道优化

出水流道优化主要满足以下2个目标：

（1）流动损失最小。

流动损失可以通过出水流道入口的总压与出水流道出口的总压差来衡量，通过调整出水水流道的形状来达到最优。

（2）流道内无明显的旋涡。

主要通过观察流线和截面。

3.1 出水流道第一阶段优化

首先对出水流道的方案1（初始方案）进行数值仿真计算，分析其内部流场的分布情况，然后确定优化方案，方案1流道内部流场如图3所示。由图3可以发现，方案1的出水流道内存在大范围的漩涡，直接导致的流动损失也比其他方案大。原因是出水流道在进口位置的速度最大，下曲线的曲率半径小，因此容易导致流动分离。为改善该问题，可以将驼峰底部位置向上抬高。表面上该改动，减小了出水流道顶部的面积，速度会增加，但实际上只是压缩了漩涡区域。优化方案2的内部流场如图4所示，可以发现，顶部的流动分离得到了大幅度改善。方案1，2的型线变化对比如图5所示。

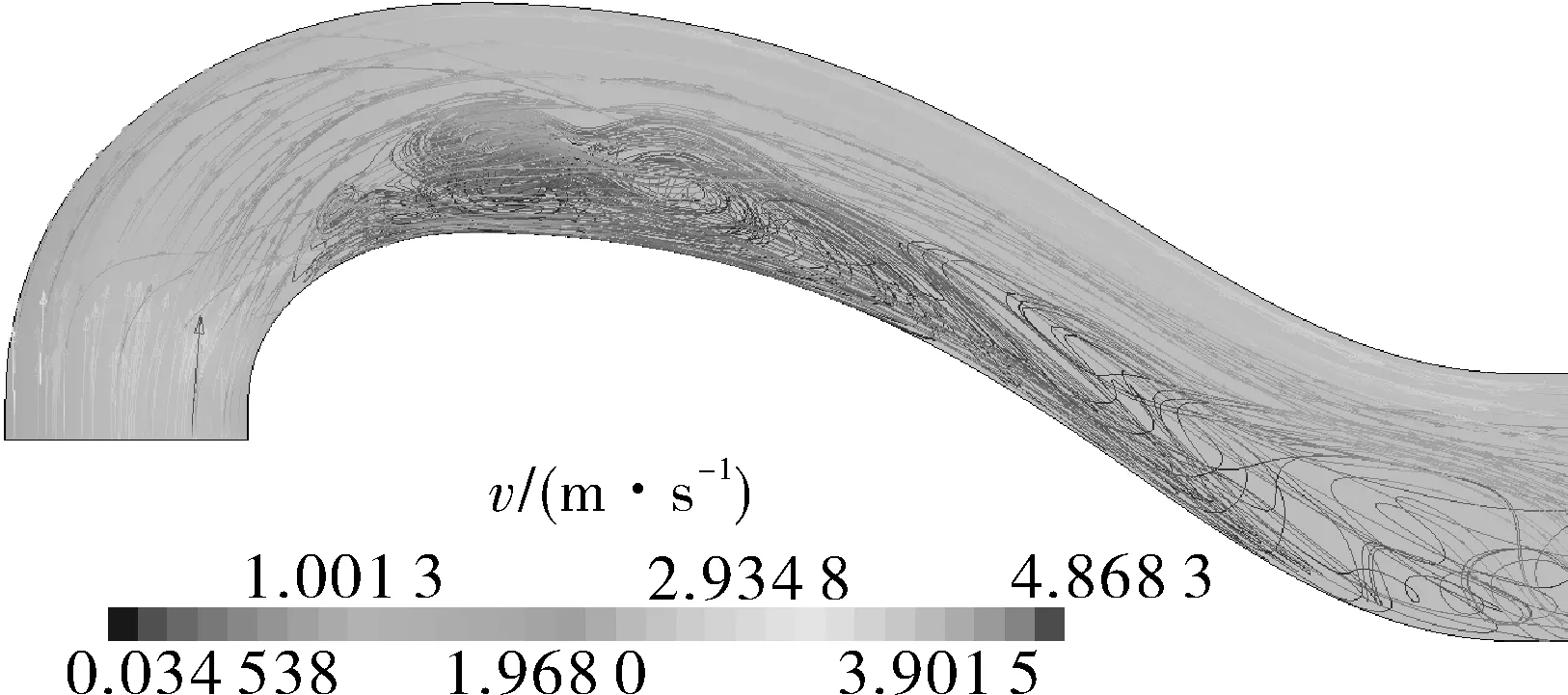
图3 出水流道方案1流道内的流线（从侧面看）Fig.3 Streamline diagram in Scheme 1 of outlet channel（viewing from the side）

图4 出水流道方案2流道内的流线（从侧面看）Fig.4 Streamline diagram in Scheme 2 of outlet channel（viewed from the side）

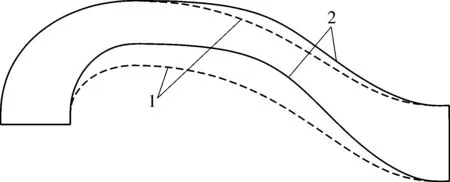
图5 出水流道方案1和方案2的型线对比Fig.5 Comparison of outlet channel profiles between Scheme 1 and Scheme 2

3.2 出水流道第二阶段优化

经过第一阶段的优化，出水流道方案2虽然取得一定效果，但驼峰底部的流动分离现象依然存在。因此在优化方案3中，尝试将驼峰水平段向右拉伸，即延长水平段的距离，方案3与方案2的流道型线对比如图6所示，方案3的内部流场分布情况如图7所示。

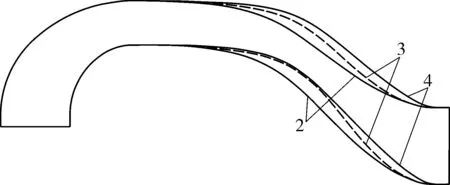
图6 出水流道方案2，3，4型线对比Fig.6 Comparison of outlet channel profiles in Schemes 2，3 and 4

图7 出水流道方案3流线（从侧面看）Fig.7 Streamline diagram of outlet channel in Scheme 3（viewed from the side）

观察图7，发现在图中双向箭头处驼峰下降段的过流断面过窄，而且在图中“大肚子”处流动分离较大，因此考虑减小此区域面积。针对这两点，给出了方案4的形状，如图6所示。方案4的内部流场分布情况如图8所示，可以发现，在“大肚子”位置的流动分离区减明显改善，流道的整体流态取得了较理想的效果。出水流道各优化方案的流动损失见表3，可以看出方案4的流动损失也是最小的，因此方案4为出水流道的最优方案。这里暂时没有考虑流道中隔墩的影响，可以在总体优化方案确定后再单独考虑中隔墩的影响。

图8 出水流道方案4流线（从侧面看）Fig.8 Streamline diagram of outlet channel in Scheme 4（viewed from the side）

表3 出水流道优化方案及性能对比Tab.3 Comparison of optimization schemes and performance of outlet channel

4 泵装置模型试验

将优化后的肘形进水流道和低驼峰出水流道，配置TJ11-HL-04水力模型，进行模型泵装置的能量特性、空化特性和飞逸特性试验，验证进出水流道的水力优化效果和泵装置的整体性能。

4.1 模型泵装置设计

模型泵装置试验依据SL140-2006 水泵模型验收试验规程执行。根据等扬程条件nD=idem确定模型泵转速。原型泵装置转速为np=150 r/min，叶轮直径Dp=2.9m，模型泵叶轮直径Dm=320 mm，则模型泵装置转速nm=1 359.4 r/min。

按相似原理模拟进、出水流道，模型比Dr=2.9/0.32=9.0625，全部过流部件几何相似，尺寸按同一模型比确定，模型流道以钢板焊接制作，加表面涂层，满足几何相似、糙率相似要求，泵装置模型试验在江苏大学国家水泵工程中心高精度水泵四象限多功能试验台上进行，试验台泵装置效率测试综合精度优于0.3%，泵装置模型装置安装现场如图9所示。

图9 模型泵装置试验现场安装Fig.9 Installation of model pump unit at test site

4.2 模型泵装置试验结果

对模型泵装置的 6个叶片角度（-6°、-4°、-2°、0°、+2°、+4°）进行了能量特性和空化特性试验，试验结果采用水泵相似律换算公式进行换算，不考虑比尺效应导致的效率的变化，即效率为等效率换算，换算后的原型泵装置综合性能曲线如图10所示。

图10 原型泵装置综合性能曲线Fig.10 Comprehensive performance curve of prototype pump unit

飞逸特性试验是测定模型泵在反转（水轮机旋转方向）且轴扭矩为零时的转速［11-14］。各叶片角度的飞逸转速变化曲线如图11所示。

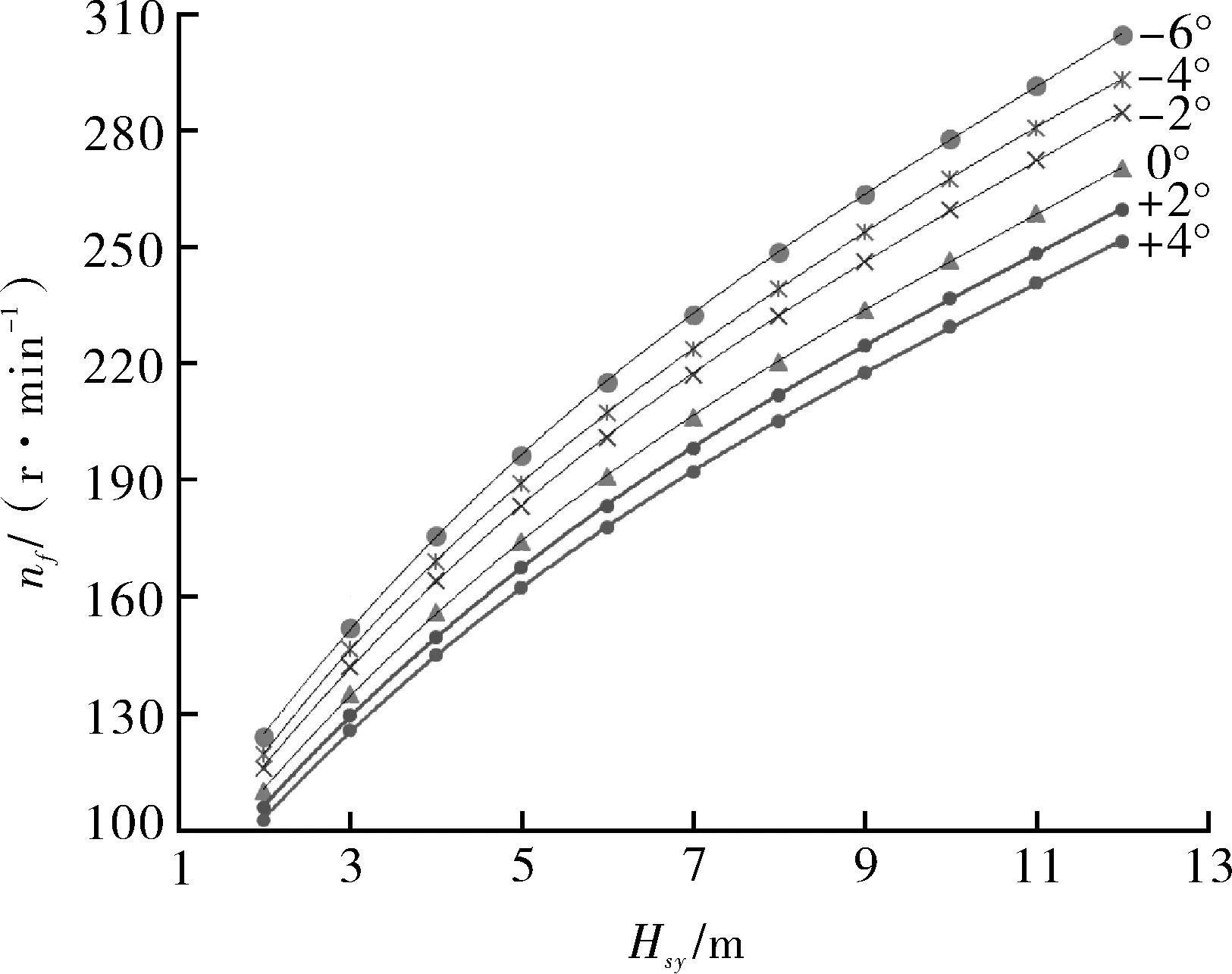
图11 各叶片角度下飞逸转速变化曲线Fig.11 Variation curve of runaway speed at each blade angle

由模型试验结果可知，在设计净扬程9.02 m，叶片安放角+1°时：单机流量为30.71 m3/s，装置效率为80.95%，轴功率为3 356.90 kW，满足设计要求，性能优良。

在叶片安放角+2°，净扬程为9.49 m，单机流量为31.38 m3/s，此时达到最高装置效率81.26%，轴功率为3 453 kW。

根据各叶片角度多工况点实际试验，临界空化余量在正角度和较低扬程运行工况下数值较高。在+1°叶片角度下，设计净扬程9.02 m的临界空化余量为10.95 m，可以满足临界淹没深度要求。

由飞逸特性试验结果可知，泵装置在叶片角-6°时单位飞逸转速254.69 r/min，最大净扬程事故停机飞逸转速可达294.57 r/min，为水泵额定转速的1.96倍。水泵生产厂家和电动机厂家应将最大飞逸转速作为一项重要参数加以考虑，即飞逸转速达到294.57 r/min时，水泵电机应能安全运转2 min以上，而不会产生破坏性影响。

建议在设计净扬程9.02 m时，在叶片安放角+1°左右运行；在最大净扬程11.25 m时，在叶片安放角0°附近运行；在较低净扬程运行时，在叶片安放角-6°附近运行，以保证不发生空化现象和高效稳定运行。

5 结论

（1）将进出水流道的所有曲线均用有理Bezier曲线描述，对进出水流道进行参数化三维造型，应用CFD技术对进出水流道的内部流场进行三维数值仿真。对进水流道以流动损失最小和出口速度分布均匀度最优为目标进行优化；对出水流道主要以流态最优和流动损失最小为目标进行优化。

（2）肘形进水流道的肘形弯管是影响进水流道水力性能的关键，应该对肘形弯管的型线方案进行重点优化。出水流道的驼峰段是出水弯管的延伸段，流速较高容易产生脱流和漩涡，应在立面方向上尽量压缩脱流漩涡区的空间，适当加长驼峰段的长度，同时在平面宽度方向上要逐渐扩散，待流态稳定和流速降低后再将流道压低，因此驼峰段是影响低驼峰出水流道水力性能的关键。

（3）将优化后的肘形进出水流道和低驼峰出水流道匹配高效水泵模型，进行泵装置模型试验。模型试验结果表明，在叶片安放角+2°，净扬程为9.49 m，单机流量为31.38 m3/s，此时达到最高装置效率81.26%，轴功率为3 453 kW。性能指标优良，说明流道优化效果明显，可为低驼峰出水流道混流泵站的新建和更新改造提供参考。