一种提高鲁棒性的改进型模型预测电流控制
2022-05-26罗姝恒
罗姝恒
(国网湖南省电力有限公司株洲供电分公司,湖南株洲,412000)
0 引言
随着能源危机的加剧,环境问题日益突出,永磁同步电机(PMSM)控制技术的快速、可靠是至关重要的[1]。永磁同步电机的控制方法矢量控制(Vector Control,VC)和直接转矩控制(Direct Torque Control,DTC)和模型预测控制(Model Predictive Control,MPC)。模型预测电流控制根据单个控制周期内的作用的电压矢量个数不同,分为单矢量、双矢量、三矢量模型预测电流控制。单矢量控制简单,但电流脉动大,三矢量虽然改善了系统性能,但计算量偏大,对硬件要求高,所以本文研究双矢量模型预测电流[2]。
占空比方法是双矢量方法中一种,在一个控制周期里,有效电压矢量只做用部分时间,其余的时间由零电压矢量来补充。文献[3]采用最优占空比的方法,预先计算6 个有效电压矢量的占空比,保证全局最优,第二个电压矢量总是零,方向固定。
PMSM 控制中将传统电流环PI 控制改为模型预测电流控制,速度环采用传统PI 速度控制器,滑膜变结构控制器能够很好地改善系统对电机参数敏感的问题[4]。
本文以永磁同步电机为研究对象,提出一种提高鲁棒性的改进型两矢量最优占空比模型预测电流控制策略。将传统滑膜变结构控制器替换PI 速度控制器,将传统计算有效电压矢量数量为6 个减少到5 个,再由价值函数选择出最优电压矢量,保证加入最优占空比后最终作用的电压矢量仍然最优。仿真结果表明本文所提控制方法的正确性与有效性。
1 PMSM 数学模型
永磁同步电机在理想的假设条件下,经过简化后的电压方程为:
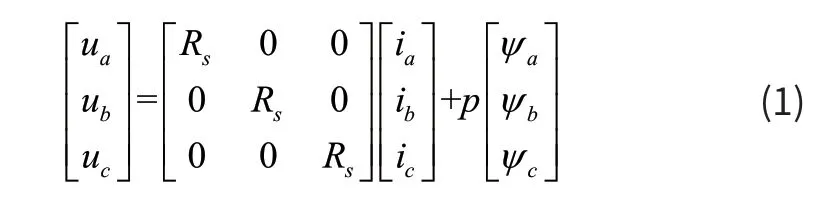
式中:ψa、ψb、ψc为三相定子绕组的磁链;ua、ub、uc是相电压瞬时值;ia、ib、ic分别是三相定子绕组的相电流瞬时值;Rs是三相定子绕组的电阻;P 是微分算子。
由于表贴式永磁同步电机的Lq=Ld,因此dq 坐标系下的电流方程:
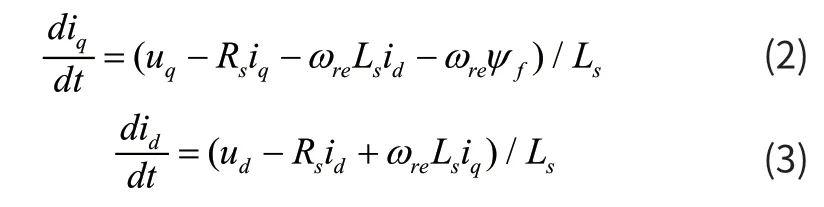
式中:ud为定子直轴电压分量;uq为定子交轴电压分量;id为电流直轴分量;iq为电流交轴分量;Ls为定子电感;Rs为定子电阻;ωre为转子电角速度;ψf为永磁体磁链。
式(2)、(3)用一阶欧拉离散化处理:

式中:id(k)、iq(k)分别为当前时刻定子电流d、q 轴电流反馈值;id(k+1)、iq(k+1) 为下一时刻定子电流d、q 轴电流预测值;Ts系统采样周期。
2 滑膜控制器设计
滑膜变结构控制是一种非线性控制法。滑膜变结构控制结构图如图1 所示。
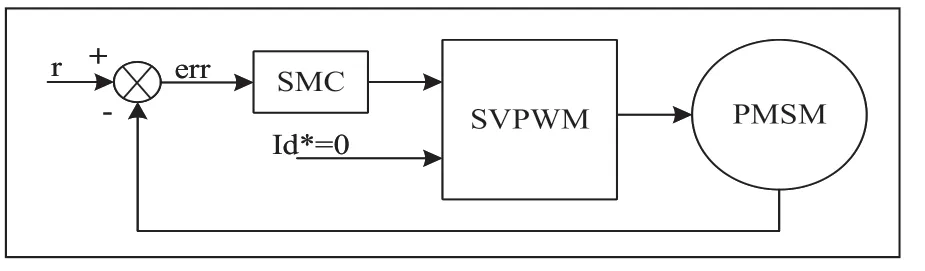
图1 滑膜变结构控制结构图
■2.1 趋近律选择
滑膜变结构控制中趋近律选择指数趋近律法能较好地减弱滑膜抖动,且u 求取比较简单直观,采用如下形式:

式中:ε、k 都是大于零的常数。
式(6)中令s>0 有:

解微分方程得:

在指数趋近律中,当t 充分大时的趋近速度比指数规律还要快。
当s>0,s(t)=0 时有:
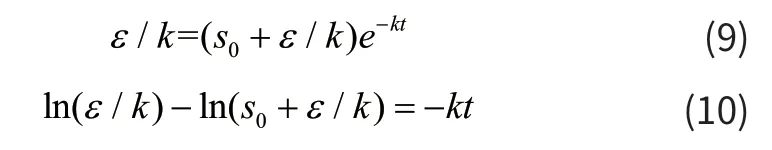
由此可以求得:
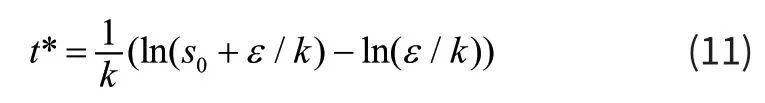
系统在有限时间内从初始状态达到滑膜面。参数k 影响到达滑膜面时间,增大k 可提高响应速度,但是k 太大会导致趋向滑膜面速度太大,在工程应用中考虑将系数与实际系统状态量的变化相结合。
另外,滑膜切换面能使系统在远离滑膜面的状态下在有限时间内趋近滑膜面,切换函数会直接影响系统的运动过程中的动态品质以及稳定性。滑膜变结构控制器原理如图2所示。
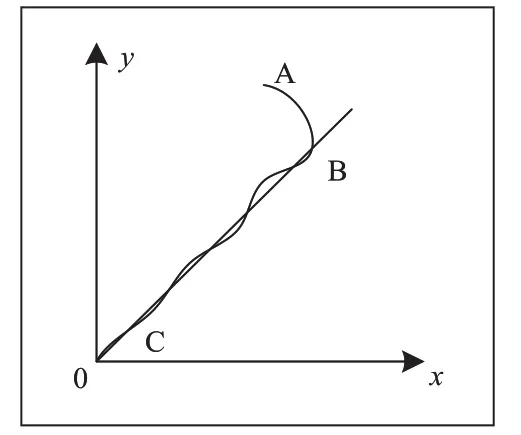
图2 滑膜变结构控制的原理
■2.2 控制量的求取
设计系统的滑膜面s 为:

对s 求偏导有:
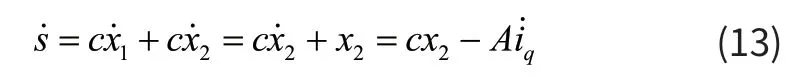
求取控制量选择限制形式趋近律法中的指数趋近律,结合式(7)、(13)有:
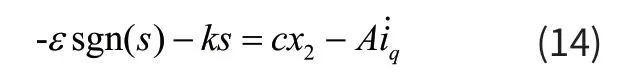
系统运行至滑膜面以上时,sgn=-1,其运动轨迹向下;当系统参数在滑膜面以下时,其运动轨迹向上。
由式(14)得到控制量iq的表达式:
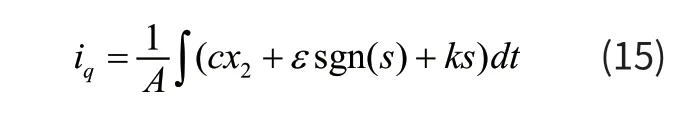
控制量iq的变结构流程图如图3 所示,可以看出求解流程较为简单。
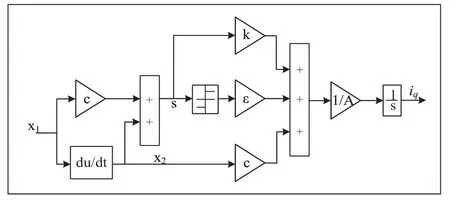
图3 控制量iq 的变结构流程图
由Lyapunov 稳定性理论可知,滑膜控制的系统稳定需满足下面条件:

保证了s 与s˙异号,满足稳定性条件,证明趋近律滑膜控制下的系统是稳定的。
3 改进的双矢量MPCC
■3.1 电压矢量选择与占空比优化
两矢量电流预测控制采用最优占空比MPCC,本文选择交轴电流无差拍的原则进行占空比计算。
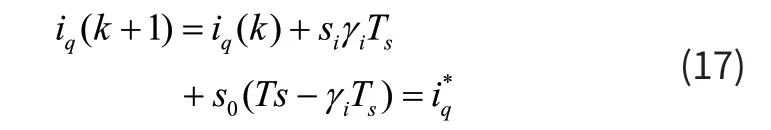
式中:iq(k)为交轴电流反馈值,iq(k+1)为交轴电流预测值,i*q为交轴电流给定值,γi为最优电压矢量的占空比,范围限制在区间[0,1]。由式(17)可得占空比为:
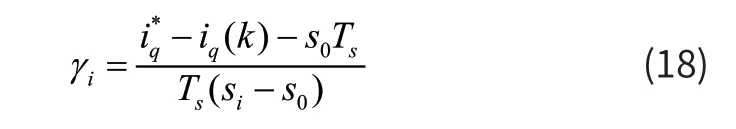
本文电压矢量选择时,第一个电压矢量的选择范围为除去上一时刻所选有效电压矢量后剩余的5 个有效电压矢量,第二个电压矢量遵循开关次数只允许一次跳变的原则将其固定为零矢量。这样一方面可以减少每个周期的运算量,另一方面可以提高系统的稳态性能。
■3.2 价值函数
MPCC 策略的控制目标是使交直轴电流可以准确跟踪交直轴电流的给定值,故选取价值函数如下形式:
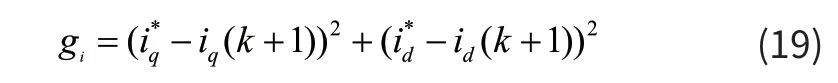
■3.3 改进的最优占空比MPCC 原理
改进的最优占空比MPCC 在进行电压矢量选择,第一个电压矢量的选择范围为除去上一时刻所选有效电压矢量后剩余的5 个电压矢量,系统框图如图4 所示(以上一周期有效电压矢量选取U1为例)。
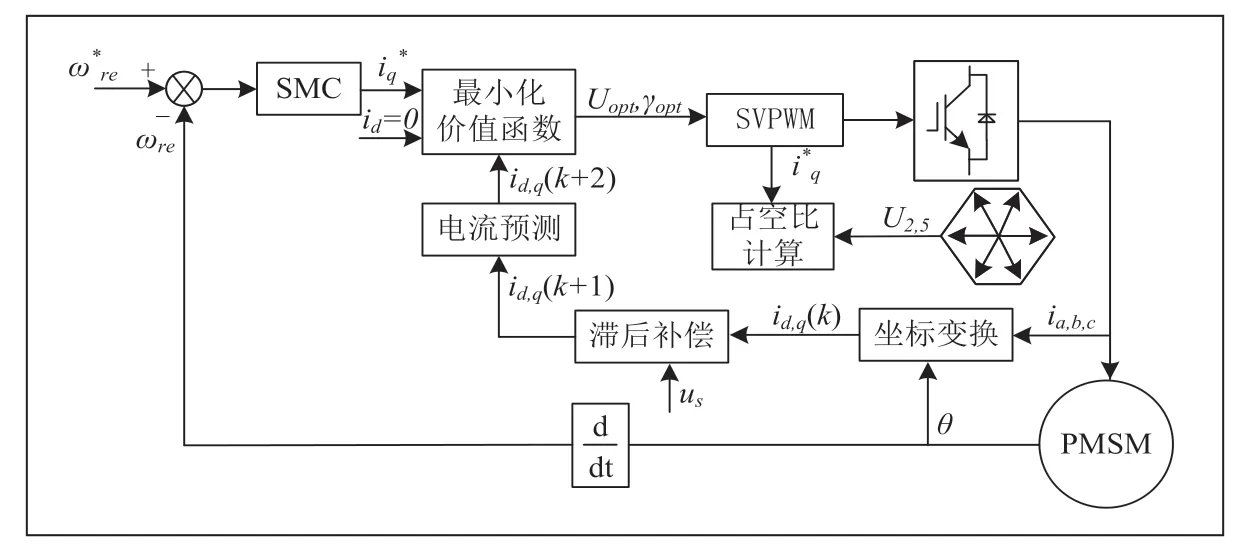
图4 改进的最优占空比MPCC 方法系统框图
改进的最优占空比MPCC 方法如下:
(1)根据式(18)分别计算5 个有效电压矢量的占空比;
(2)根据PMSM 离散数学模型式(4)和式(5),预测经过补偿后的id,q在5 种电压矢量及其占空比的组合作用下的电流值,代入到代价函数中计算gi值;
(3)比较5 个gi值,选择代价函数最小的电压矢量为最优电压矢量,最优电压矢量及占空比通过空间矢量调制技术实现。
4 控制系统仿真结果与分析
本文对所提出的电流预测控制算法在MATLAB 软件中进行仿真验证,与传统方法进行比较。仿真电机参数如表1所示。
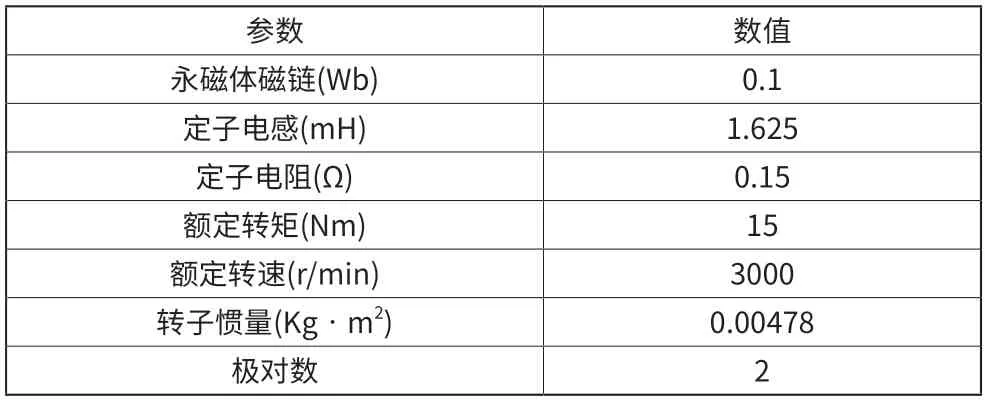
表1 PMSM参数
系统仿真总时长为0.3s,图5 给出了电机空载启动到1500r/min,在0.2s 时突加额定负载15 Nm,并在0.3s 时卸载。传统PI 速度环控制器+两矢量MPCC、传统PI 速度环控制器+改进两矢量MPCC 和SMC 速度控制器+改进两矢量MPCC 3 种控制方法的转速波形。表2 中3 种控制方法的启动时间大约为32ms,具有相同迅速的转速响应。传统PI 速度环控制器+改进两矢量MPCC 减少了系统的计算负担,但并未改变系统的性能,并且SMC 速度控制器+改进两矢量MPCC 有效减少了电机转速的超调量和电机稳态误差。(δ 转速超调量;ts调节时间,稳态值的±2%;Δn电机转速稳态误差值;Δn1 突加负载时转速最大跌落值;Δn2 卸载时转速最大抬升值;t1 突加负载后达到稳态时间;t2 突加负载后达到稳态时间)。
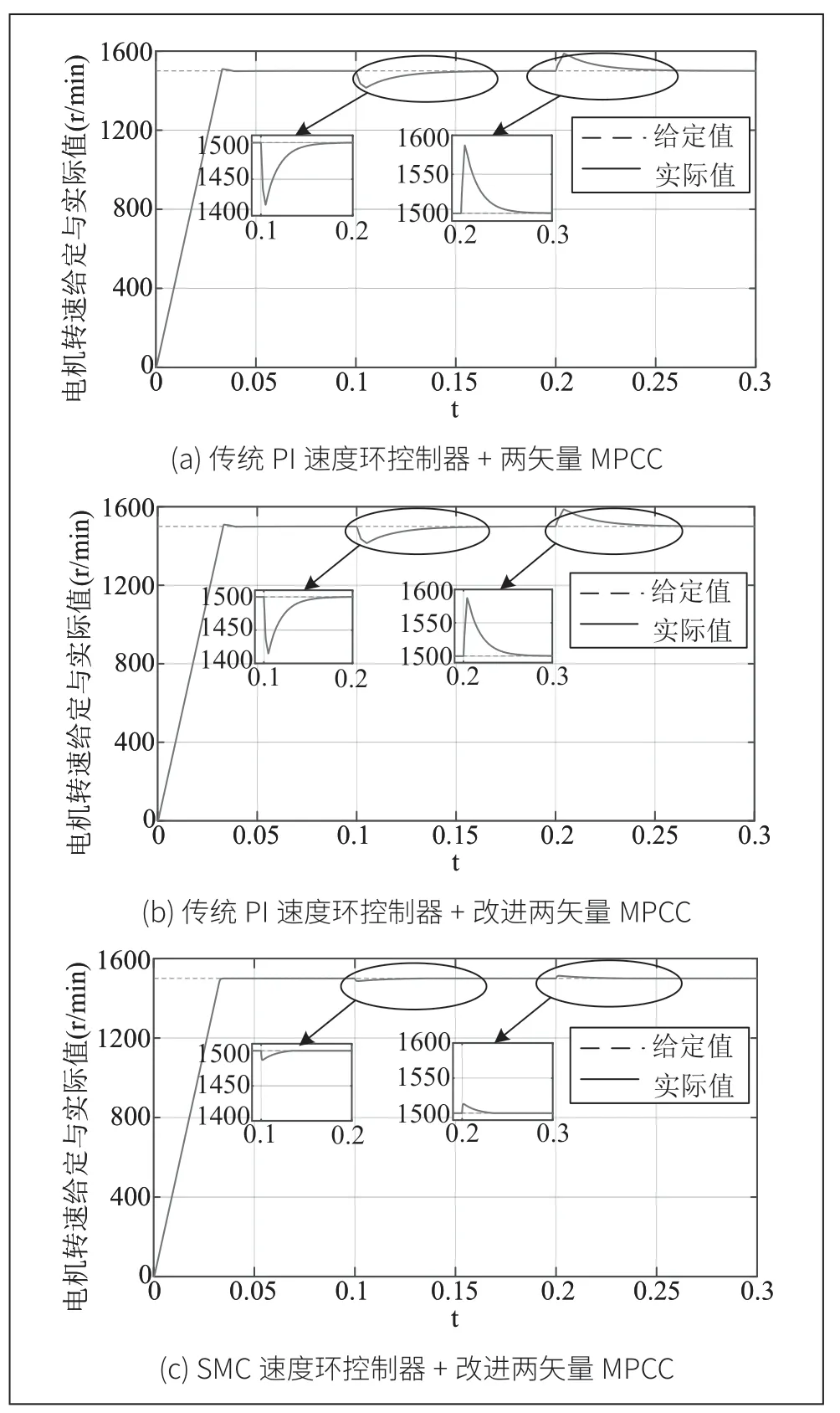
图5 3 种控制策略在加载和卸载时转速的仿真波形
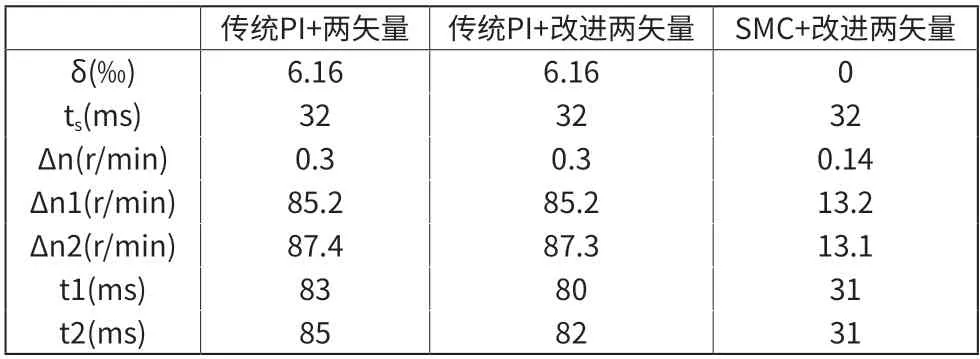
表2 3种控制策略的转速比较
图6 给出了电机加载和卸载时,3 种控制方法交轴电流波形。从表3 中可看出减少最优矢量的选择减轻计算负担,并未影响电机系统的性能,并且采用SMC 速度控制器+改进两矢量改善系统在加载和卸载时交轴电流波动(Δiq1 突加负载时最大误差电流;Δiq2 卸载时最大误差电流)。
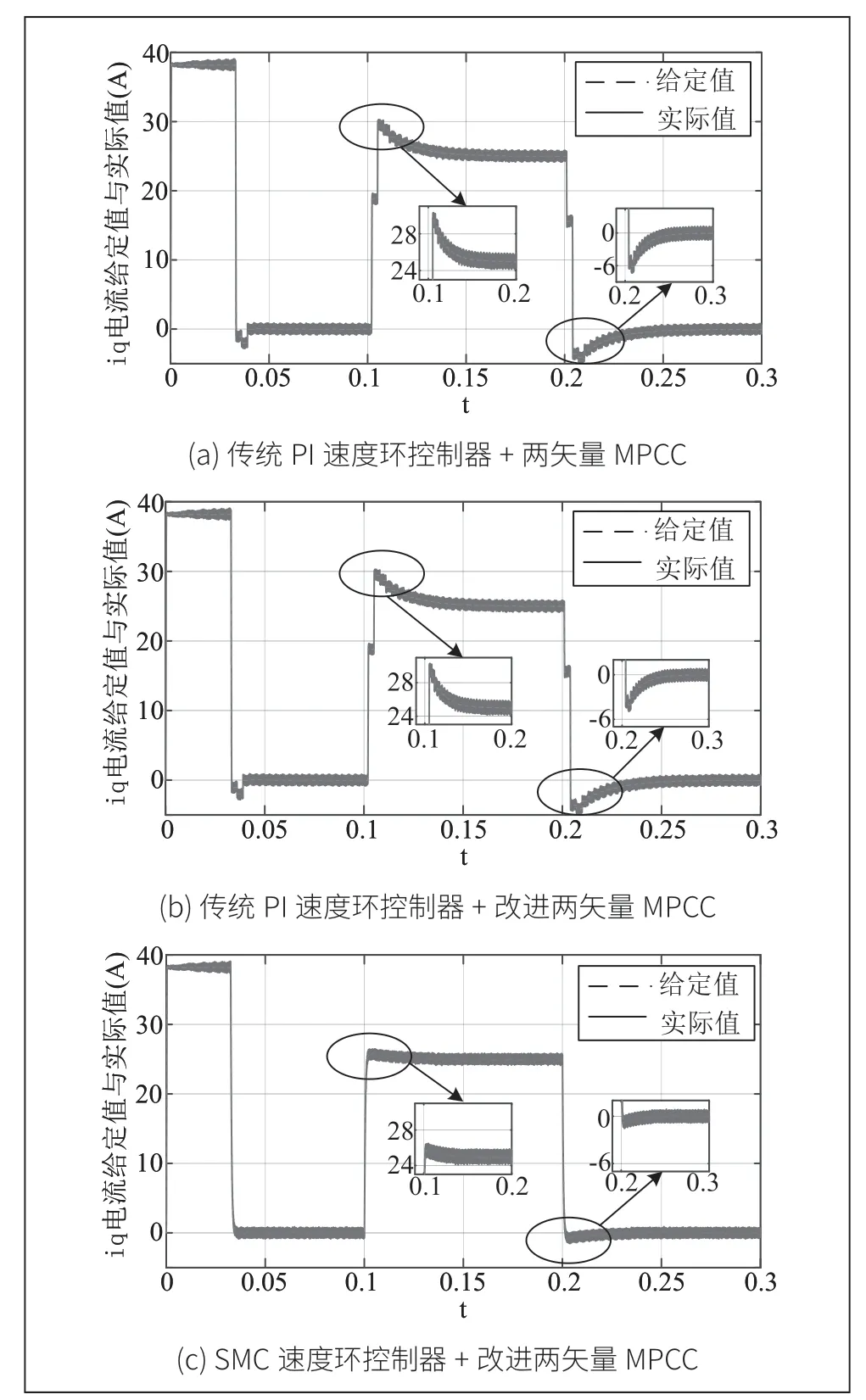
图6 3 种控制策略在加载和卸载时iq 电流的仿真波形

表3 3种控制策略的iq比较
5 结语
本文针对永磁同步电机两矢量预测控制策略,研究了其电压矢量组合与控制器的选择对稳定性能的影响,分析了传统PI 控制器对电机参数敏感的问题,提出将传统PI 控制器替换滑膜变结构控制器,提高系统鲁棒性的改进两矢量电流预测控制方法,通过仿真结果得出以下结论:
(1)减少最优矢量的选择不仅保持了传统两矢量MPCC的高动态响应速度,而且减少了系统的计算负担;
(2)采用滑膜变结构控制改善传统PI 控制器对电机参数敏感的问题,具有比传统两矢量MPCC 更小的转速和电流波动。
