基于视觉模拟优化算法的太阳能电池模型参数的辨识

郭虎平，蓝永康，谷力，张雪敏

（西安思源学院 基础部，陕西西安，710038）

0 引言

能源是人类社会发展的重要物质基础。目前，人类大量开采使用的还是石油、煤炭、天然气等不可再生能源，由于地球上存储的化石能源有限，过度开采会导致生态环境破坏，造成能源供给危机。大量使用化石能源会进一步导致环境污染，危害地球生态。因此，寻找新的清洁能源是未来发展趋势。太阳能是一种清洁能源，是未来能满足人类日益增大电能需求的可再生能源。光伏发电能将光能直接转换成电能，被认为是当前世界上最具潜力的可再生资源，同时，光伏发电也是当前科技领域中的研究热点[1-3]。

太阳能电池模型可以预测实际的电池在不同工作环境下的行为，并且反映电池的伏安特性和功率电压特性。太阳能电池模型的建立包括两部分：数学模型建立和模型参数的辨识。目前广泛使用的数学模型是单二极管非线性等效电路模型和双二极管非线性等效电路模型[4]。快速准确的辨识光伏电池模型参数对于电池输出功率预测及电池故障诊断模型的研究都有重要意义。因此，近年来不同的辨识电池模型参数的方法被提出，主要包括两类方法：分析类方法和群智能优化方法。分析类方法通过数学分析方法，如微分求导、模型简化等求得模型参数的近似值。分析类方法的参数辨识的准确性依赖与一些特殊点的信息[5]，对测量中的噪声较敏感，同时还存在初始值敏感、数学变换复杂以及在数值计算中存在误差等问题。近年来，智能优化算法被广泛应用于光伏电池参数辨识[6-10]，该类方法将光伏电池参数的求解转变为目标函数的寻优问题，简单便捷。但是，智能优化方法普遍存在算法易陷入局部极值，即算法早熟现象[11-12]。而且很多改进后的智能算法没有在测试函数上进行测试，也没有和其他智能算法做横向对比，这使得得到的结果可靠性降低。视觉模拟优化算法是一种高精度的优化算法[13]，在测试函数上进行过严格测试对比，且该算法实现简单易于使用，这些优点使得它更适合应用于光伏电池模型参数辨识的问题。本文将利用视觉模拟优化算法针对太阳能电池的单二极管非线性模型和双二极管非线性模型分别进行参数辨识，得到的参数再进行重构I-U 特性和P-U 特性，在重构的过程中，不采用数学分析方法去转换成显示表达式，而是再次利用视觉模拟优化算法通过把输出电流当成优化变量建立新的目标函数进行优化重构。得到结果和实测数据进行对比以检验视觉模拟优化算法的搜索性能。同时，通过和相同类型的数据的相似算法进行对比研究，以客观、严谨的分析视觉模拟优化算法性能及在智能优化算法中的优化能力。

1 光伏组件数学模型

目前，常见和广泛应用的太阳能电池的数学模型是单二极管非线性等效电路模型和双二极管非线性等效电路模型。图1 是太阳能电池的单二极管等效模型。从图中可以看到单二极管光伏电池模型电路由一个光生电流源Iph，一个串联电阻Rs和一个并联电阻Rsh，以及一个并联二极管D组成，根据基尔霍夫定律，很容易得到电路中输出电流的如（1）式关系：

图1 单二极管光伏电池模型

其中，Id为并联二极管电流；Ish为并联电阻电流；Iph为光生电流。

再根据基尔霍夫定律和肖克利方程便可推导出并联二极管电流Id及并联电阻电流Ish分别如（2）式和（3）式：

其中，IL为二极管反向饱和电流；U为太阳能电池输出电压；Rsh为二极管的并联分流电阻；Rs为太阳能电池的分压电阻；a为二极管的品质因子；q为元电荷量（1.602× 10-19C）；k为玻尔兹曼常数（ 1.3806503 × 1 0-23J/K）；T为电池温度。

由（1）（2）（3）式便可推导出电池的输出电流I如式（4）所示。

单二极管光伏电池模型中未知参数有5 个，分别是I ph,I L,Rs,Rsh,a。

图2 是太阳能电池的双二极管等效模型。从图中可以看到，双二极管模型电路由一个光生源Iph，两个并联二极管D1和D2,以及一个并联电阻和一个串联电阻组成。根据基尔霍夫定律得到电池输出电流表达式为如（5）式：

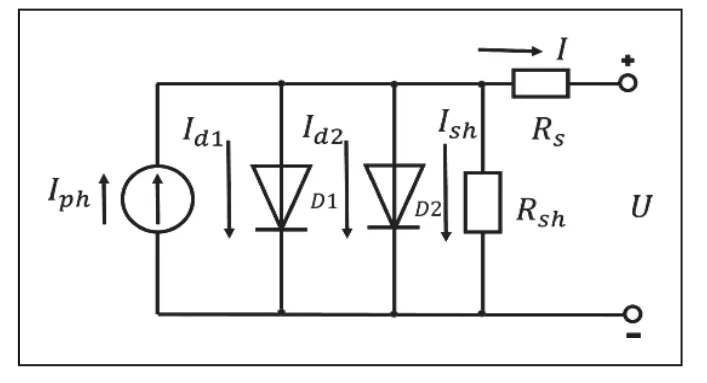
图2 太阳能电池双二极管模型

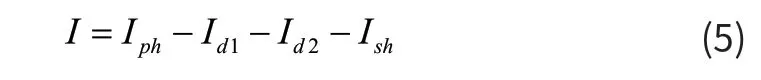
其中，I为电池输出电流；Iph为光生电流；I d1,Id2分别为第一并联二极管电流和第二并联二极管电流；Ish为并联电阻电流。

再根据肖克利方程便可得到第一并联二极管电流和第二并联二极管电流I d1,Id2的表达式如（6）（7）式所示：

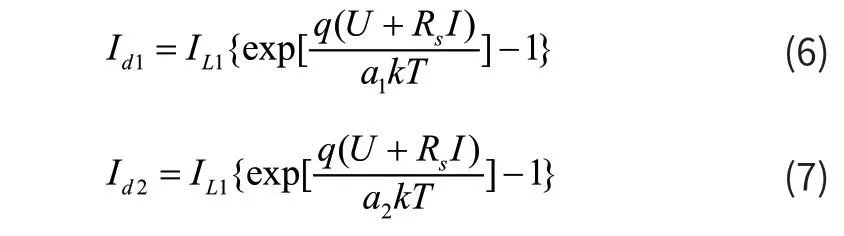
其中，I L1,IL2分别为扩散电流和饱和电流；a1,a2分别为扩散和重组二极管的理想系数。

并联电阻的电流表达式如（8）式所示：

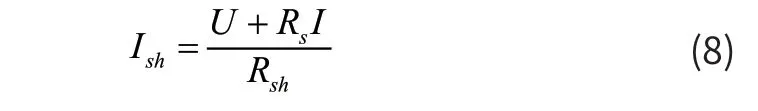
其中，U为太阳能电池输出电压；Rsh为二极管的并联分流电阻；Rs为太阳能电池的分压电阻。

根据（5）～（8）式可以计算出双二极管模型电池的输出电流I如下（9）式：

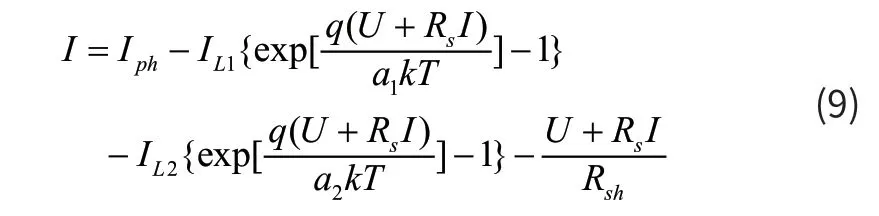
在以上的双二极管光伏电池模型中未知参数有7 个，分别是I ph,I L1,I L2,Rs,Rsh,a1,a2。

2 视觉模拟优化算法

视觉模拟优化算法(visual simulation optimization algorithm 简称VSA)是模拟生物视觉系统的一种新型智能算法[13]。智能算法的关键就是平衡勘探和开采的关系，即全局搜索和局部搜索的平衡。在视觉模拟优化算法中，通过在可行域内提前“瞭望”的方式来进行勘探，有效避免无效开采，提高了搜索效率。该算法简单有效，是一种高精度智能搜索算法。算法的基本步骤如下：

（2）在该点附件邻域内（邻域范围随着迭代次数逐渐减小到0）随机取另外一点；

（4）计算n个探测点的适应度值，并选择最佳探测点，如果比当前最优值还好，则更新最优值及最优值点；

（5）利用进化策略(1 +1)-ES算法对当前最优值点进行开采搜索，进一步更新最优值及最优值点；

（7）如果满足停止规则，则退出循环，否则返回步骤（2）。

进化策略(1 +1)-ES算法是一种具有强大局部搜索能力的进化类算法[14]，它通过高斯变异产生新的解，通过和父代进行比较，较好的一个成为下一次迭代的父代，否则直接舍去，并相应的调整变异强度的值。变异强度的改变按照Rechenberg 提出的著名“1/5 Success rule”[14]即：成功变异与所有变异的比率应该是1/5，如果比率大于1/5，则应增加变异强度，否则就降低变异强度。该局部搜索算法简单高效适合用于视觉模拟优化算法中的局部搜索功能，当然也可以用其他的局部搜索算法代替。

视觉模拟优化算法原理简单，需要调整超参数少（每次探测点数n，进化策略(1 +1)-ES每次局部搜索次数m，以及变异强度初始值sigma），方便快捷，但是效果显著，在文献[13]中和常见的遗传算法、粒子群算法、模拟退火算法、人工蜂群算法在10 个常见的测试函数中进行对比研究，结果显示视觉模拟优化在所有测试函数中都优于其他算法，而且在5 个测试函数中找到全局最优解，其搜索精度远高于其他对比智能算法。在解非线性方程中和单一的进化策略(1 +1)-ES算法进行对比，结果显示，视觉模拟优化算法中的在可行域内的提前“瞭望”进行探测是必不可少且非常有效的过程，它和进化策略(1 +1)-ES算法的局部搜索能力紧密联系起来，形成有效的搜索能力。因此，视觉模拟优化算法适合应用于需要极高精度的搜索领域问题中，当然非常适合应用与太阳能电池的参数辨识中。

3 光伏电池模型参数辨识

光伏电池参数辨识就是通过实验测量得到的I-U 数据值，找到光伏电池参数的最优值，使模型能够准确的描述光伏电池的实际输出特性，并使辨识数据和实验数据之间的误差最小。因此，可以定义如下的目标函数：

（1）对于单二极管模型，根据（4）式并采用均方根误差建立目标函数如（10）式：

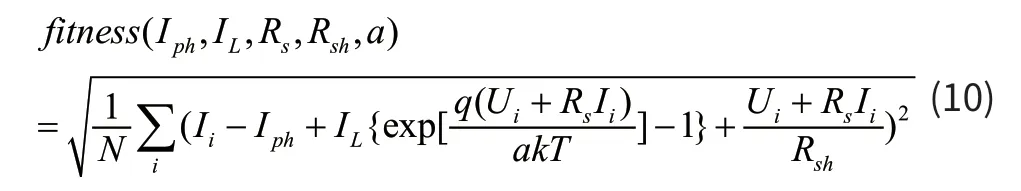
其中，U i,Ii分别为太阳能电池的输出电压和电流的实际测量数据，下标代表采样点。N为实验数据个数。

该目标函数本质上就是均方根误差（RMSE），而且该式为隐式的非线性超越方程，有些文献喜欢把它近似简化成显示方程，但这样做会产生额外误差，由于本文采用的是智能优化算法，对于隐式非线性超越方程并不影响求解，这也是智能算法的最大优点之一。

（2）对于双二极管模型根据（9）式并采用均方根误差建立目标函数如（11）式：

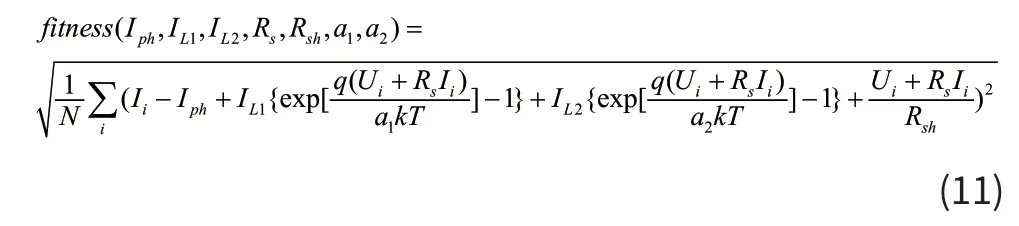
太阳能电池的参数辨识就变成一个优化问题，待辨识参数看成一个解向量，在可行域中寻找一个合适的解向量，使适应度函数的值最小即可满足条件。

4 结果与讨论

实验利用标准测试条件下采集光照为1000W/m2的反映57mm 的硅太阳能电池的I-U 实测数据集[15]，温度为33℃。参数搜索范围如下：Rs∈ [0,0.5]，Rsh∈[10−16,100]，Iph∈ [ 0,1]，I L,I L1,IL2∈ [ 0,1],a,a1,a2∈ [ 1,2]。辨识参数值和相关文献的对比结果如表1 所示。

表1 中的结果都取到小数点后4 位，得到的参数都代入式（10）和式（11）中得到最优适应度值，从表1 的结果可以看到，本文所用的方法在辨识准确度上比文献中的方法都要好，不管是单二极管模型还是双二极管模型，这验证了视觉优化算法的高精度性能。而且文献[18]中已经和粒子群算法，遗传算法，模拟退火算法等算法在光伏电池参数辨识上进行了对比，表1 所列是文献[18]中最优的参数，可见本文算法比常见的智能算法的辨识准确度更高。

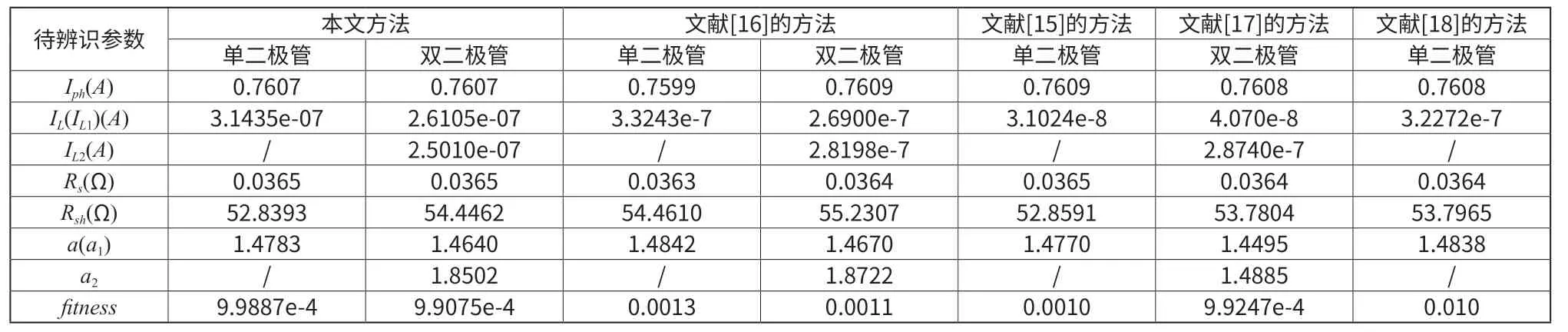
表1 不同方法的辨识参数值

根据算法辨识到的参数重构电池模型的I-U 特性及P-U特性。由于视觉模拟优化算法精度高，所以无需对（10）、（11）式转换为显示表达，直接设定输出电流为优化变量建立目标函数，再用视觉模拟优化算法来求出电压值对应的输出电流值，从而得到I-U 特性及P-U 特性。得到单二极管模型的I-U 特性曲线如图3 和P-U 特性曲线如图4 所示。双二极管模型的I-U 特性曲线如图5 和P-U 特性曲线如图6所示。从图中可以看到，本文采用的方法重构的I-U 特性与实测结果非常一致，进一步证实了视觉模拟优化算法的有效性。同时看到单二极管模型和双二极管模型误差非常小，从图3 和图5，图4 和图6 中几乎看不出来区别，为了分析它们之间的差别，把它们之间的误差表示成图7 和图8 所示，它们分别是单二极管模型和双二极管模型的I-U 特性误差和P-U 特性误差分布图。从图7 和图8 中看到它们之间误差非常小，其次，还发现它们之间误差的分布有一定周期性，这为分析单二极管模型和双二极管模型的关系提供重要信息。

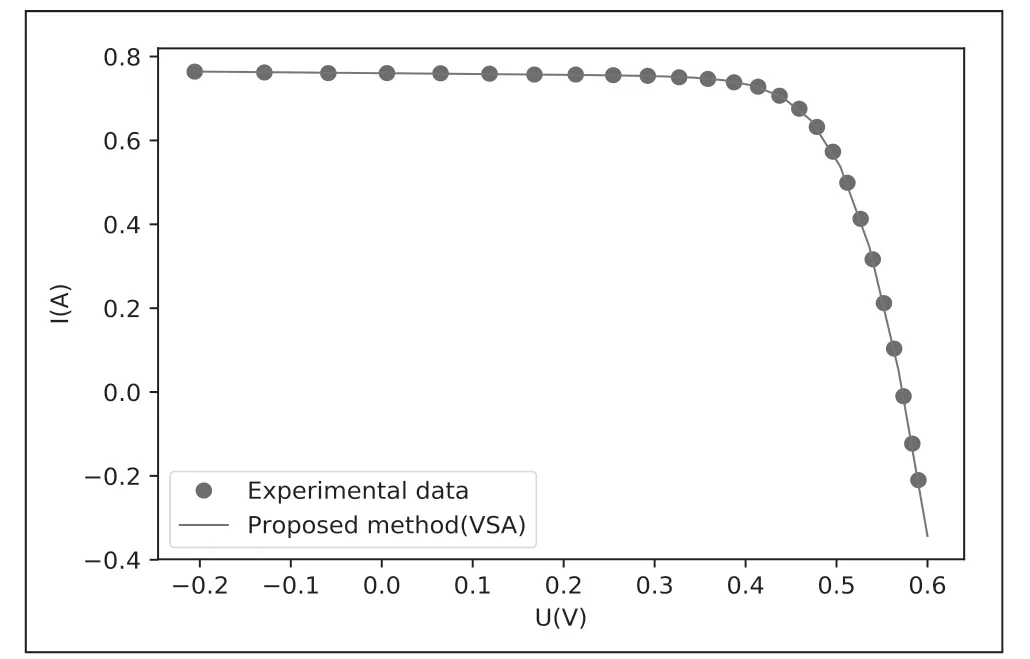
图3 VSA 算法产生单二极管I—U 特性与实测数据的对比

图4 VSA 算法产生单二极管P—U 特性与实测数据的对比

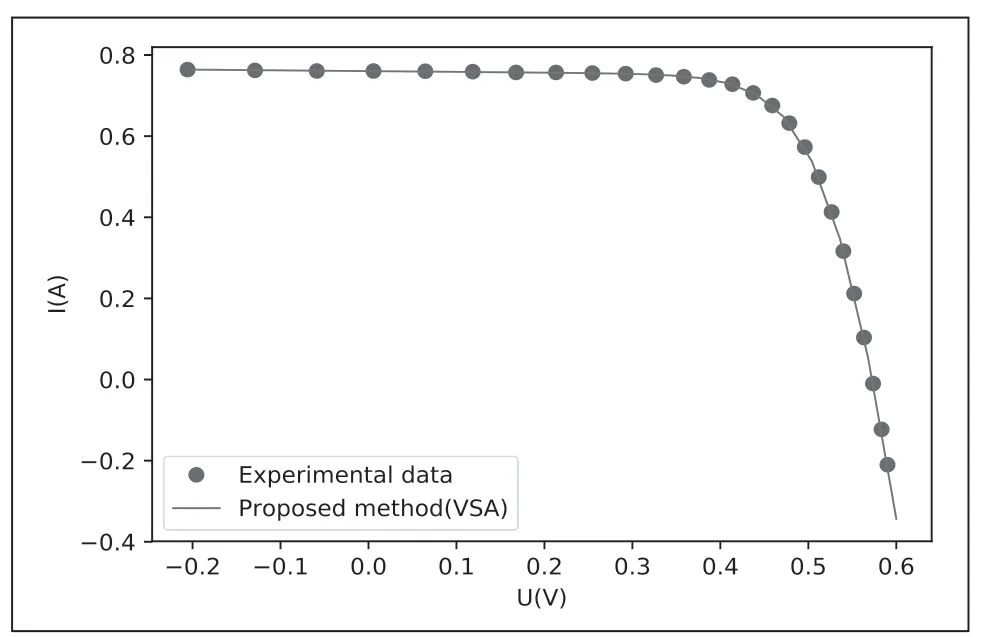
图5 VSA 算法产生双二极管I—U 特性与实测数据的对比

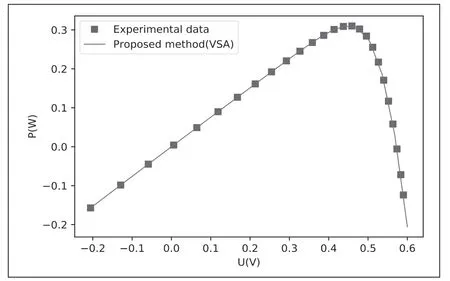
图6 VSA 算法产生双二极管P—U 特性与实测数据的对比

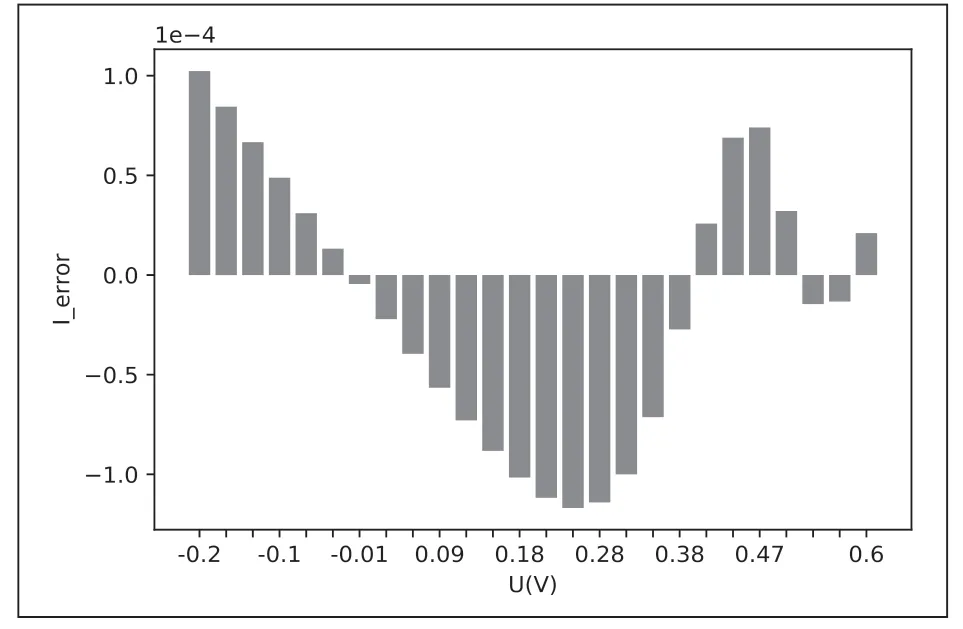
图7 单二极管模型和双二极管模型I—U 误差

图8 单二极管模型与双二极管模型P—U 误差

5 总结

太阳能电池模型参数的快速准确辨识在太阳能电池的仿真、性能评估、故障诊断等方面具有重要作用。智能优化算法具有使用简单，方便快捷等特性使得它被广泛应用在光伏电池参数辨识问题中，但是智能优化算法的缺点就是搜索精度不高，易陷入局部极值。视觉模拟优化算法是一种高精度的优化算法，本文利用它对太阳能电池模型的单二极管模型和双二极管模型的参数进行辨识，根据辨识参数重构I-U特性和P-U 特性和实测数据非常一致，同时和同类型算法、同数据集的文献进行对比研究，结果都显示本文的方法优于对比文献中的其它智能算法。