改进层次基本尺度熵在液压泵故障诊断中的应用

陈 睿，万春梅

（1.毕节市工业和信息化局大数据产业发展中心；2.毕节职业技术学院电子信息工程系，贵州毕节 551700）

0 引言

液压泵是液压系统中用于提供动力的零部件，其能否平稳运行直接决定了液压设备工作的可靠性，因此有必要对液压泵当前运行状态进行实时检测［1-2］。由于液压泵所处的工况通常是不断变化的，因此其产生的振动是非线性和非平稳的［3-4］，并且液压泵在发生不同故障时具有的振动幅度也不一致，因此可以通过分析非线性和非平稳的振动信号来判断不同故障类型。

随着非线性动力学理论的不断发展，大量基于熵的方法被提出并用于旋转机械的故障诊断。文献［5］将样本熵用于滚动轴承的故障诊断，诊断结果表明，样本熵能够准确判断轴承的故障类型，但是样本熵所使用的阶跃函数在计算中存在定义不准确的缺陷，在一定程度上降低了所获取特征的质量；文献［6-7］将排列熵（Permutation Entropy，PE）用于提取齿轮振动信号的故障特征并取得良好效果，但排列熵在描述信号的复杂度过程中忽视了信号振幅对熵值的贡献，致使具有不同幅度的振动信号可能具有同样的排列熵值；基本尺度熵（Base scale Entropy，BSE）是一种类似于排列熵的非线性动力学分析方法［8-9］，通过将时间序列进行符号化处理使其具有较强的抗噪性能并且运算效率高，用于分析非线性和非平稳时间序列的效果比较理想［10］。

然而，实际振动信号所包含的故障信息通常呈现在多个尺度上，仅执行单一尺度的分析无法充分提取更深层次的故障特征，因此有必要将单尺度的BSE 扩展至多尺度分析以提高信息的利用效率。文献［11］提出采用多尺度基本尺度熵（Multiscale Base-scale Entropy，MBSE）对滚动轴承的不同故障进行识别，实验结果表明MBSE 能够有效提取隐藏在振动信号中的故障特征，性能优异。然而，MBSE 所采用的粗粒化方法存在较大缺陷：首先，在信号长度较短时，此计算得到的熵值存在较大偏差，稳定性较差；其次，基于均值定义的粗粒度计算方法［12］无法有效分析信号高频成分中的故障信息，导致信息的利用率不足，影响特征提取的质量。为此，本文提出改进层次基本尺度熵（Modified Hierarchical Base-scale Entropy，MHBSE）的方法，不仅能改善传统粗粒度计算方法依赖时间序列长度的问题，而且能充分分析时间序列的高频成分从而获得更全面、准确的故障信息［13-14］，可用于提取液压泵振动信号的故障特征。

针对液压泵的故障特征提取以及模式识别问题，本文提出一种基于改进层次基本尺度熵的随机邻域嵌入（t-Distributed Stochastic Neighbor Embedding，t-SNE）［15］和随机森林（Random Forest，RF）［16-17］的故障诊断方法。首先利用MHBSE 从原始振动信号中提取高维故障特征，然后将t-SNE 用于从高维的故障特征中筛选出低维的故障敏感特征，最后将低维的敏感特征输入至RF 多故障分类器以判断液压泵的故障类型。液压泵诊断实验结果表明所提方法比现有方法效果更好。

1 改进层次基本尺度熵

1.1 基本尺度熵

基本尺度熵是一种基于香农熵的非线性动力学方法，能够衡量非线性时间序列发生动态突变的概率，实现原理简单，计算高效，且具有较强的抗噪性能。基本尺度熵原理如下：

给定一包含数据点数为N的时间序列X={x(1)，x(2)，…，x(i)，…，x(N)}，对于每个数据点x(i)，选择m个非间断点组成一个m维向量：

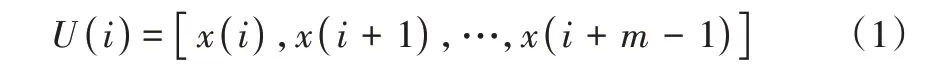
总共可以得到N-m+1 个m维向量，其中每个m维向量都计算得到对应的基本尺度Bs，Bs表示m维向量中全部相邻点数据大小的差值平均根值，表示如下：

按照基本尺度，定义了区分不同符号的标准a×Bs，随后把各个m维向量根据不同的选择标准转换为m维向量符号序列详细转换方式描述如下：

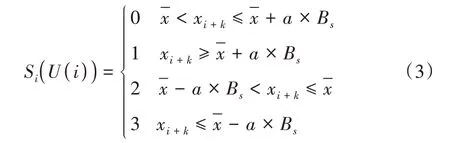
式 中，i=1，2，…，N-m+1，k=0，1，…，m-1。是第i个m维向量的均值，Bs为第i个m维向量的基本尺度，符号0，1，2，3 主要用于区分不同区域的指标，具体数值不存在实际意义，用途是便于统计概率的大小。

计算m维向量符号序列Si的分布概率P(Si)，包括0、1、2、3 这4 种符号的m维向量符号序列Si，共存在4m种可能的组合状态π。每种组合状态都表示为m维向量的一种波动模式，随后将各个组合状态在全部N-m+1 个m维向量中所具有的概率进行统计如下：

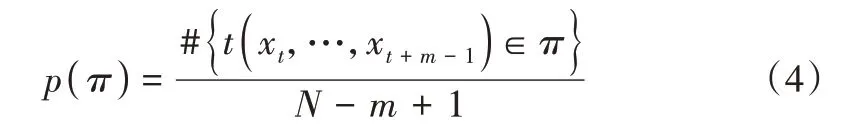
式中，1 ≤t≤N-m+1，#表示一个统计函数，用于统计出现的个数。

因此，基于香农熵的定义，时间序列的基本尺度熵为：

1.2 改进层次基本尺度熵

本文提出将MHBSE 用于提取液压泵振动信号的故障特征。层次化分析是一种多尺度分析的新方法，它可以同时描述时间序列的低频和高频分量的复杂性。但是，层次分析面临着与传统的粗粒度方法类似的缺陷，即随着层数的增加，层次时间序列的长度将相应减少，从而使估计的熵值不可靠。为改善这一缺陷，MHBSE 采用移动平均和移动差分过程来代替原始的分层过程，以使层次时间序列的长度不会随着层数的增加而减少。与HBSE 相比，MHBSE 具有更好的性能和更高的稳定性。另外，由于MHBSE 采用移动平均法来获得层次时间序列，因此对原始时间序列的长度没有严格要求，从而克服了信号长度必须为2n的要求，更加符合实际信号的处理现状。

MHBSE 详细实现过程如下：

（3）为了对x(i)进行层次分析，必须重复执行上述运算符。对于给定的k∈N，可以生成唯一矢量[η1，η2，…ηk]，然后将整数e计算如下：

式中，{ηm，m=1，…k}∈{0，1}表示mth层的平均值或差值运算符。

（4）基于向量[η1，η2，…ηk]，可以根据式（10）定义时间序列x(i)的层次分量：

（5）计算每个层次序列的BSE，从而获得时间序列X的MHBSE。其定义如下：

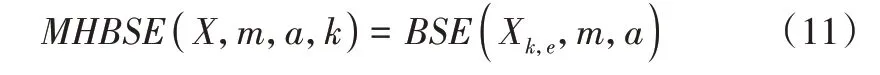
为了更好地描述层次分解，图1 显示了对时间序列X进行三层层次分解的层次树。在图1 中，当层次分解的层数k=1 时，X1，0和X1，1分别表示时间序列X的低频和高频分量。对于不同的k和e，Xk，e的物理含义是原始信号在不同层次分解尺度上的层次分量，如X2，1表示层数为2 的节点1 上的层次分量。对于k和e的每个组合，都有一个唯一的向量[η1，η2，…ηk]与之对应，例如，如果k=2 且e=1，则唯一向量[r1，r2]=[0，1]，然后使用式（10）获得分量·。

Fig.1 Three hierarchy decomposition of time series X图1 时间序列X的三层层次分解

1.3 参数选择

MHBSE 的优异性能受到嵌入维数m、参数a、层次分解的层数k和时间序列的长度N这4 个关键参数影响。如果m的取值过小，则重构的时间序列中包含的状态太少，算法失去有效性［18］。但m太大则无法检测到时间序列中的突变成分，且需要花费大量的计算时间。

下面研究在a=0.2，k=4 和N=4 096 时不同的嵌入维数对MHBSE 性能的影响。不失一般性，采用具有代表性的两种随机信号高斯白噪声（WGN）和1/f噪声作为实验对象进行分析，这两种随机信号的时域波形如图2 所示。为了对MHBSE 的嵌入维数进行合理选择，在嵌入维数m 为3、4、5、6、7时计算两种随机信号的MHBSE 值，对比分析结果如图3所示。

从图3 可知，在嵌入维数m=3 时，两种随机信号的MHBSE 近乎是定值，只有较小波动，变化不明显，这表明当嵌入维数较小时各个节点上的熵值没有明显差异，体现不了层次分析的优势。当m较大时，重构过程会使时间序列均匀化，此时无法表征时间序列中的细微变化，m越大越难区分内在结构相似的时间序列。如m=7 时，图3 中白噪声和1/f噪声的差异就较小，区分度不明显。此外，当m较大时，计算同一组数据所花费的时间将远大于较小的嵌入维数。为了同时具有较好的性能和保持较高的计算效率，一般选择m=5。

通常时间序列的长度不能过小，否则层次分解后得到的层次时间序列长度过小会造成较大的熵偏差。因此，本文选择长度为N=512、N=1 024、N=2 048、N=4 096、N=6 144 和N=8 192 的白噪声进行分析，其中参数选择为m：5，参数a=0.2，层次分解的层数k=3，分析结果如图4 所示。从图中可以看出，在选择不同长度的时间序列时，MHBSE 的变化不是很明显，说明时间序列的长度对MHBSE 性能造成的影响较小。但能够看到，当长度较大时熵值的变化也更加平缓。当N大于2 048 时，整体曲线随尺度因子的变化趋势较平稳，表明取较大长度能够获得更稳定的结果。从计算效率和稳定性综合考虑，选择时间序列的长度为N=4 096。

Fig.2 Time-domain waveforms of white Gaussian noise and 1/f noise图2 高斯白噪声与1/f噪声的时域波形

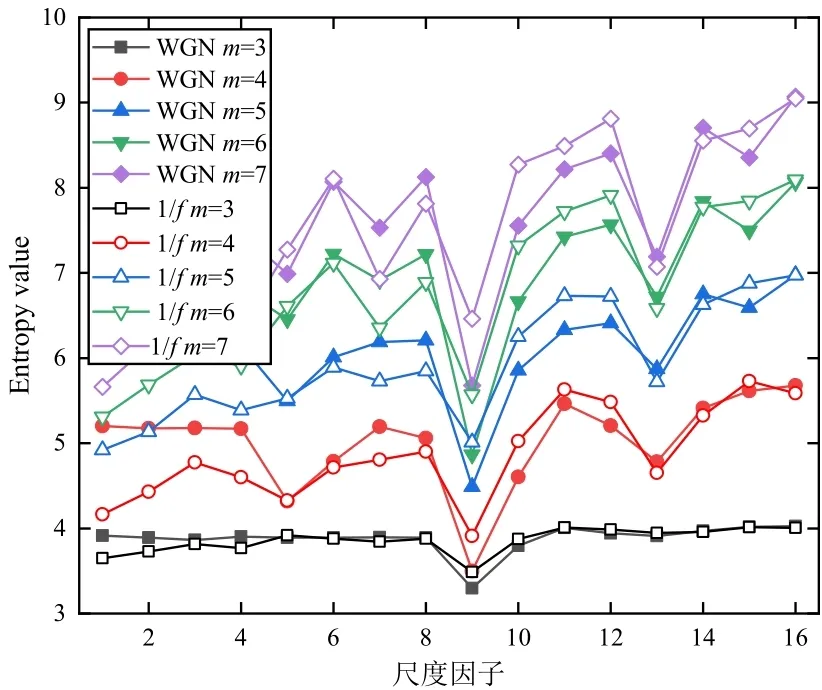
Fig.3 MHBSE change of the two random signals under different embedding dimensions图3 两种随机信号在嵌入维数下的MHBSE变化

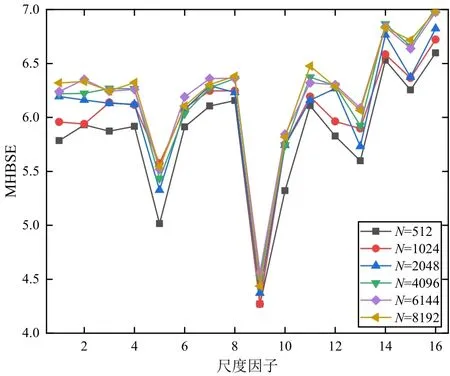
Fig.4 MHBSE of WGN under different data length图4 WGN在不同数据长度的MHBSE

参数a是一个比较特殊的参数，取值范围通常限定在0.1～0.4，a值太大将造成细节信息的丢失，无法充分提取时间序列中的动态特征，但是a的值太小会使算法对噪声较敏感，因此本文选择a=0.2。对于分解层数k，取值过小会导致提取的信息不足，无法全面反映故障状态，但取值过大又会造成特征的冗余并且影响分类精度，因此从提高信息利用率以及减小冗余的角度考虑，将k设置为4。综上，本文的参数选择如下：时间序列长度N=4 096，嵌入维数m=5，参数a=0.2或0.3，分解层数k=4。

1.4 性能对比分析

为了验证MHBSE 在描述时间序列的复杂性时比其它方法更具优势，将其与MBSE 和HBSE 进行对比，同样选择数据长度为4 096 的高斯白噪声进行算法性能测试。3 种方法的参数选择保持一致，MBSE 的尺度因子选择为τ=16，参数a选择为0.2，3种方法的对比结果如图5所示。

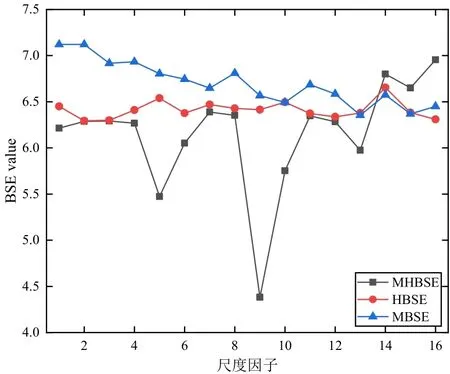
Fig.5 Analysis of Gaussian white noise using MHBSE，HBSE and MBSE图5 使用MHBSE、HBSE和MBSE对白噪声的分析结果

从图5 中可以看出，白噪声的MBSE 随着尺度因子逐渐减小，但是高斯白噪声在高频部分也存在模式信息，因此在高频处仍然具有较高的复杂度，即具有较大的熵值，但MBSE 由于无法分析白噪声的高频分量导致其无法准确描述其在高频处的复杂性变化。此外，MHBSE 由于采用滑动平均对时间序列进行层次分割从而获得更多的特征信息，因此能够从白噪声中检测到细微的变化，体现在图5 中即存在波动性。综上所述，MHBSE 具有更强的复杂性表征性能，同时可以全面且充分地提取信号中的信息。

2 液压泵故障诊断方法实施路径

本文提出一种基于改进层次基本尺度熵、t-SNE 和随机森林的针对不同健康状态的液压泵故障诊断技术，能够对不同液压泵故障状态进行精准检测，该技术实施流程如图6所示。

Fig.6 Technical implementation route of the improved method图6 改进方法的技术实施路径

该液压泵故障诊断方法改进了传统多尺度计算方法的粗粒化过程，采用基本尺度熵提取振动信号的状态特征，使得液压泵的故障特征质量更高，具有更有效的可分性；采用t-SNE 流形学习算法对获取的高维特征样本进行维数约简，从而获得低维的敏感特征；采用具有优异泛化性能和分类表现的随机森林分类器，对特征样本进行状态分类。

（1）实验数据准备。在给定的采样频率fs下，利用加速度传感器收集液压泵在4 种故障状态下运行的振动数据，并将其划分为训练集和测试集。

（2）高维故障特征获取。利用MHBSE 方法从训练集和测试集中提取振动信号的熵值特征，从而生成分类所需的特征向量。

（3）维数约简。所获取的初始故障特征往往存在冗余信息，不仅降低分类效率而且影响识别精度。因此，采用t-SNE 流行降维方法对样本进行维数压缩从而得到低维易分类的故障特征样本。

（4）状态分类。利用所获得的低维特征样本对随机森林多故障分类模型进行训练和测试，输出测试样本的故障状态。

3 实验结果与分析

3.1 实验数据介绍

为了对所提出的故障诊断方法性能进行验证，将采集的液压泵振动实验数据进行故障诊断实验。振动数据在军械工程学院建造的液压泵测试平台上采集，如图7所示［19］。

Fig.7 Hydraulic system experimental test platform图7 液压系统实验测试平台

液压泵实验平台总体结构包括动力系统、压力调节系统、控制系统、振动监测和控制系统、采集系统、信息显示系统和冷却系统。在动力系统中，传动电动机以90kW 的功率提供动力。在变频器调节下的速度控制在0～3 000r/min 范围，可用于不同测试要求的液压泵实验。其中，压力调节系统提高了实验平台的耐高压性，可以承受高达40 MPa 的高压。

平台采用的液压泵为凸轮盘式轴向柱塞泵，型号为SY-10MCY14-1EL，装备7 个柱塞，额定转速为1 500 rpm，主安全阀端口压力为10 MPa。振动数据由安装在液压泵端盖上的高精度压电加速度传感器收集，传感器型号为603C01。采样频率设置为20 kHz，收集的振动数据由NI 公司生产的DAQ-9171 存储系统保存。实验中使用的液压泵结构以及传感器的特定安装位置如图8所示。

Fig.8 Installation position of the sensor and hydraulic pump图8 传感器和液压泵的安装位置

此实验共模拟4 种类型的故障状态：正常（N）、单柱塞松动滑靴（1P）、双柱塞松动滑靴（2P）、活塞靴磨损（S）。图9 显示液压泵的两种故障类型。针对每种故障状态采集了200组样本，对应4 种状态的时域波形如图10 所示。每组样本的采样点数为4 096，彼此不重叠，因此总共有800 组样本。随机选择320组样本作为训练集，其余样本作为测试集。

Fig.9 Failure types of hydraulic pumps图9 液压泵故障类型

Fig.10 Time-domain waveforms of vibration signals of four states of hydraulic pump图10 液压泵4种状态的振动信号时域波形

3.2 初始高维故障特征提取

获得液压泵多个运行状态的振动数据后，为了对其状态进行判断，首先需要获取能够表征其状态的特征，因此采用MHBSE 从液压泵振动信号中提取非线性故障特征构建特征向量。此外，为了检验所提出的MHBSE 方法在特征提取中的有效性，将其与MBSE、HSE 和MPE 3 种方法进行对比分析。4 种方法的均值标准差如图11 所示。另外3 种方法的参数设置分别为：MBSE：嵌入维数为m=5，参数a=0.2，尺度因子为τ=16；HSE：嵌入维数为m=2，相似容限r=0.15std，层次分解层数为k=4；MPE：嵌入维数为m=5，时间延迟t=1，尺度因子为τ=16。

从图11 可以看出，基于MHBSE 的方法在各个尺度上能够明显将4 种状态进行区分，具有良好的可分性。而基于MBSE 的方法在尺度因子为8～16 时存在较为显著的混叠现象，其中故障1P 和故障2P 的熵值曲线发生了明显的重叠，此时MBSE 方法无法对这两种状态进行区分，可分性较差。此外，MHBSE 方法的4 条曲线在各个尺度的熵偏差均小于MBSE 方法，越小的熵偏差意味着稳定性越高，性能越好，因此MHBSE 的方法性能优于MBSE。而基于HSE 的方法在绝大多数尺度上都具有较明显的可区分性，即各个状态的样本能够通过熵值大小的关系进行区分。但是从图中可以看到，基于HSE 的方法具有极大的熵偏差，并且比MHBSE 大，表明MHBSE 的性能比HSE 更稳定，能够获得更加准确的分析结果。而基于MPE 的方法具有较低的熵偏差，性能稳定性较高，能够较好地区分液压泵各个故障状态。但是，排列熵在提取特征时并没有考虑信号的振幅对熵值的影响，而振幅信息对于机械设备的故障诊断方向来说非常关键，能够表征故障的各种类型，因此不能被忽略。综上，MHBSE 比其它方法的性能更好，能够更准确和更稳定地提取液压泵的故障特征。

3.3 特征维数约简

通常，直接从振动信号中提取的特征具有较高维数，其中包含大量与故障特征无关的信息，直接用于分类将干扰故障分类结果且降低分类效率，因此有必要进行维数压缩以选择最能表征故障信息的特征。采用t-SNE 对特征进行压缩，以增强特征的可分性。此外，为了从数据的内在结构判断所提取特征的质量，将经过上述4 种方法提取的故障特征进行二维可视化，通过可视化图即可直观判断特征的可分性，4种方法的可视化结果如图12所示。

从图12 可以看出，MHBSE 所提取的故障特征经过t-SNE 降维后相同状态的样本都聚类在一起，不同状态的样本都彼此分离，具有非常明显的聚类中心，表明MHBSE 所提取的特征具有非常高的质量，可分性极高。而MBSE 所提取的故障特征虽然也能够获得聚类中心，但4 种样本的聚类中心互相接近，且各样本之间都发生了一定程度的混叠，部分样本脱离了聚类中心，说明所提取的部分特征较接近，质量较低。经过HSE 方法所提取样本1P 和样本S 的故障特征发生了明显混叠，部分样本被混入另一状态的样本中，表明该方法对这两种状态的区分能力较差。经过MPE 方法提取的特征对样本2P 和样本S 的区分能力较差，这两类样本也发生了部分混叠，部分属于状态2P 的样本混入至状态S 的样本类中。总体来看，4 种方法所提取的特征质量可以归纳为MHBSE 的质量最佳，MBSE 的质量最差。通过对特征进行降维可视化，能够直观验证MHBSE 方法性能最佳。

3.4 故障状态分类

为检验所提出的故障诊断方法在模式分类中的效果，将经过上述4 种方法得到的低维敏感特征输入到随机森林多故障分类器中进行故障识别，识别结果见表1-表4，其中随机森林的决策树设置为100棵。

Fig.11 Entropy results of hydraulic pump vibration data analyzed by four methods图11 4种方法分析液压泵数据的结果

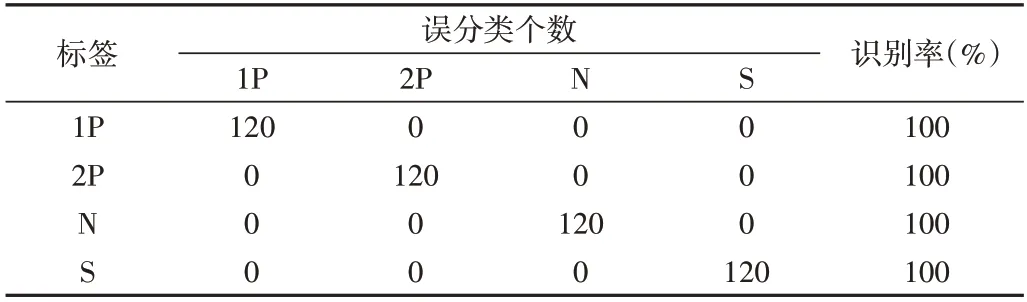
Table 1 Fault identification result based on MHBSE method表1 基于MHBSE方法的故障识别结果

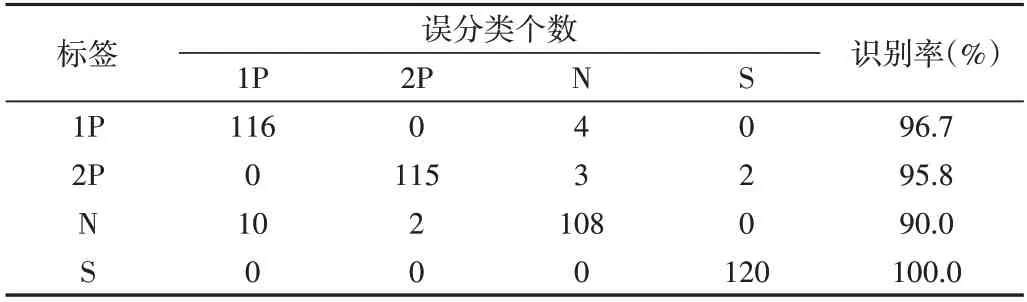
Table 2 Fault identification result based on MBSE method表2 基于MBSE方法的故障识别结果

从表1-表4 可以看出，本文所提出的故障诊断方法取得了100%的分类准确率，即所有的样本都被准确分类了。基于另外3 种方法的分类准确率都存在误分类，其中基于MPE的方法表现最好，只有两个样本2P 被误分类至样本S，这也与图12（d）的结论一致，即MPE 对这两种状态的区分性较差，在分类识别时表现为对这两类样本出现误分类情况。基于MBSE 方法识别率略低于HSE，这也与图12 的分析一致，即MBSE 的样本可分性是最差的，故障识别率最低。综上所述，基于MHBSE 的故障诊断方法具有非常优异的性能，与现有方法相比，该方法的故障识别率最高。

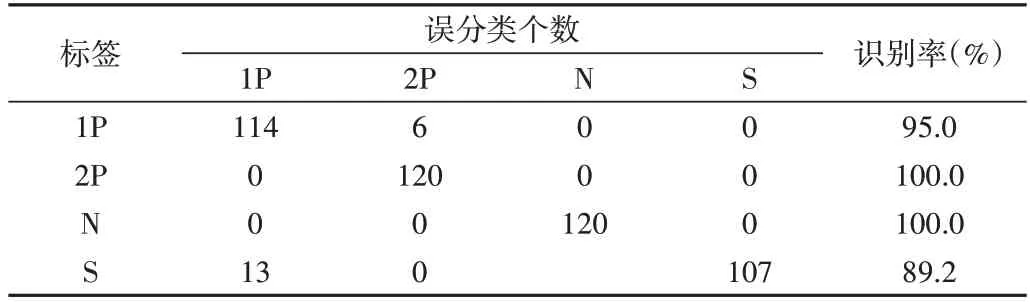
Table 3 Fault identification result based on HSE method表3 基于HSE方法的故障识别结果

Table 4 Fault identification result based on MPE method表4 基于MPE方法的故障识别结果

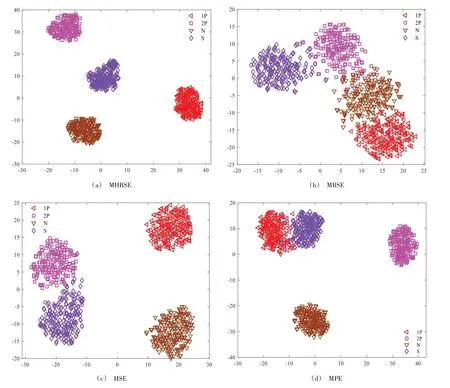
Fig.12 Two-dimensional feature visualization map obtained by t-SNE of four methods图12 4种方法经过t-SNE得到的二维可视化图

一般来说，只执行单次分类会由于随机性等偶然因素造成实验结果不可靠，有必要进行多次分类以避免偶然因素对结果可靠性的影响。因此，将每种方法重复执行20 次后，4种方法的分类结果如图13和表5所示。

Fig.13 Diagnosis results of four methods for 20 trials图13 4种方法重复运行20次的识别结果

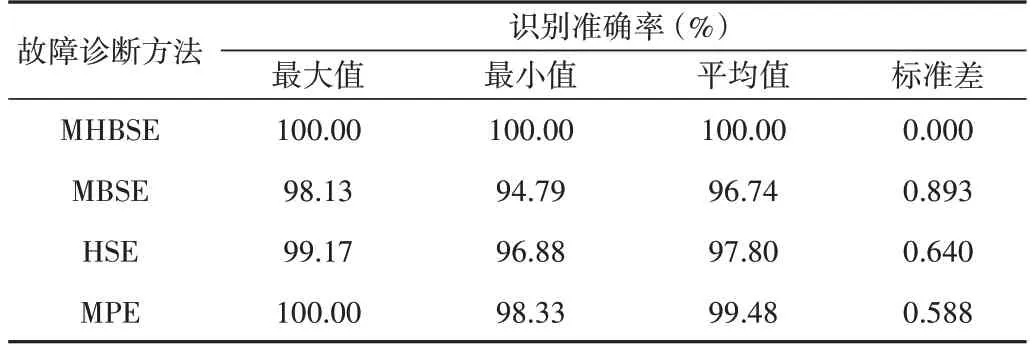
Table 5 Classification results of four diagnostic methods for 20 trials表5 4种故障诊断方法运行20次的故障分类结果

从图13 和表5 可以看到，将4 种方法在相同条件下重复运行20 次后，所提出的方法识别率仍然是最高的，达100%，在20 次分类中没有发生误分类情况，进一步验证了该方法具有非常稳定且优异的性能，非常适合用于液压泵的故障诊断。而MPE 方法也取得非常不错的识别效果，平均准确率达99.48%，平均每次分类只有2 个样本被错误分类，对于待分类样本较多时，这样的准确率是比较令人满意的，表明MPE 也具有非常优异的性能。而基于MBSE 的方法平均准确率为96.74%，其中最高正确率达到了98.13%，最低仅有94.79%，并且标准差为0.893，是4 种方法里最高的，表明MBSE 方法的分类准确率不稳定，存在较大波动，提取的特征质量不够稳定，鲁棒性差。基于上述分析可以得出以下结论：①MHBSE 能够提取高质量的故障特征，所提取的故障特征能够很好地表征液压泵的各种状态，具有较高的质量；②基于MHBSE 的故障诊断方法稳定性最高，能够获得非常准确和稳定的分类效果，鲁棒性高；③另外3 种方法都存在一些影响识别率的因素，体现在每种方法都存在误分类的情况。

4 结语

本文提出了一种新的量化非线性时间序列不规则度的非线性动力学方法——改进层次基本尺度熵（MHBSE）方法，研究了该方法的参数选择。提出一种基于MHBSE、t-SNE 和RF 的液压泵故障诊断方法，利用液压泵振动试验数据将其与基于MBSE、HSE 和MPE 的故障诊断方法进行对比。故障分类结果表明，本文所提方法具有更好的性能。但MHBSE 方法在强噪声环境下的应用性能未得到有效验证，在实际条件下振动信号通常伴随着巨大的噪声，未来需要对其在强噪环境下的特征提取性能进行检验。