基于结构-参数同步优化的河湖水位模型及应用

胡腾飞，施勇，毛劲乔，栾震宇，陈炼钢，陈黎明，金秋，徐祎凡，戴会超

(1. 南京水利科学研究院水文水资源研究所，江苏 南京 210029; 2. 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029； 3. 河海大学水利水电学院，江苏 南京 210098)

河流和湖泊水位建模常用技术包括具有物理机制的水动力模型[1-2]和数据驱动技术[3-5].与机理模型相比，数据驱动技术能从有限的训练样本中学习输入输出间的内在联系，因此模型输入通常只包含所关注变量及其关联要素的时间序列[6].数据驱动技术不需要对物理过程的全面认识，且能更快地提供预测结果.河湖水位预测常用的数据驱动技术有支持向量回归(support vector regression，SVR)和多种人工神经网络.基于统计学习理论的SVR在水位预测领域被认为是比人工神经网络更好的选择[7].

输入变量选择(input variable selection，IVS)目标是确定SVR模型的最优结构形式.常用的IVS方法可分为独立于模型的Filter技术和基于模型的Wrapper技术以及Embedded技术[8].Filter技术通过统计方法分析可用数据以衡量变量或变量组合的重要性，选择结果对不同数据驱动方法具有通用性；然而，此类技术忽略了底层模型预测能力对选择结果的响应.Wrapper技术通过搜索变量的所有(或大部分)组合来确定对应数据驱动方法最大预测能力的输入变量集合[9]；然而，由于底层模型没有针对候选变量进行充分率定，其真实预测能力可能被掩盖[10].Embedded技术可使不相关或冗余变量的影响在训练中逐渐消失；然而，此类技术仅面向特定的数据驱动方法.

为更好地解决河湖水位SVR建模中的输入变量选择问题，文中提出基于进化算法的SVR模型结构-参数同步优化方法.为验证所提方法的有效性，该方法被应用于长江流域2个不同区域的实际案例中.

1 研究方法与数据

1.1 研究区域

文中选取荆江和洞庭湖区域作为SVR模型结构-参数同步优化方法的验证区域，具体涉及洞庭湖城陵矶(七里山)站和荆江陈二口站水位模拟预测.该区域河湖水流既相互补给又相互制衡，水流运动复杂，适合检验水位建模方法的适用性及合理性.洞庭湖位于中国长江中游地区荆江南岸，是中国面积第二大淡水湖.洞庭湖在调蓄长江洪水方面发挥着重要作用[11]，也因此呈现“涨水是湖，退水为洲”的独特景观格局.长江洪水通过荆江南岸的松滋、太平和藕池三口分流入湖(曾有第四口调弦口，于1959年封堵)；洞庭湖还承接其4条主要支流—湘、资、沅、澧的来水，入湖水流经湖泊调蓄后在城陵矶汇入长江.

1.2 研究方法

基于SVR构建复杂河湖水系的水位模型时，为应对考虑关联要素时滞后输入变量搜索空间的高维特性，提出了基于进化算法的SVR模型结构-参数同步优化方法.首先简要介绍SVR及核函数的基本理论，再重点介绍文中提出的SVR模型结构-参数同步优化方法.

1.2.1 支持向量回归SVR

支持向量机的基础为VAPNIK[12]创建的统计学习理论.近年来，支持向量机凭借其优良特性和强大的泛化能力受到研究者青睐[13-14].

1) 支持向量回归函数.SVR通过数学方法归纳样本输入输出数据中隐含的依赖关系，这一依赖关系获得后便可对未知输出进行预测.对于数据集DS={(x1,y1), (x2,y2),..., (xl,yl)}，xi∈Rn为输入变量，yi∈R1是相应的输出变量，数据集DS的输入输出映射可通过以下回归函数估计

f(x)=ωTφ(x)+b,

(1)

式中：ω为权重向量；φ为将x映射到高维特征空间的非线性映射；b为截距.

基于ε不敏感损失函数(ε>0为误差阈值)，可通过优化以下函数得到回归函数[12]，即

(2)

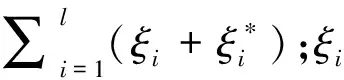
由于权重向量ω的高维特性，通常求解式的对偶问题，引入拉格朗日乘子得到

(3)

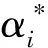
借助核函数，高维特征空间内积φ(xi)Tφ(xj)可直接在输入空间通过训练样本计算得出，不需要进行输入向量映射到特征空间的计算，核函数的引入大大减小了计算量.

通过求解式(3)，回归函数可最终表示为

(4)

2) 核函数.在水文水资源领域，绝大多数应用都采用径向积函数并获得了理想的模型精度[15].因此文中河湖水位建模采用径向积函数，其表达式为

K(xi,xj)=exp(-γ‖xi-xj‖2)，

(5)

式中：γ> 0为控制核宽度的参数.

1.2.2 SVR模型结构-参数同步优化

SVR模型的输入输出结构一般可表示为

(6)

式中：fSVR为基于SVR构建的输入输出映射；变量xi，(i=1, 2, …,N)为目标变量y的关联要素;t为时间;mi和ni，(i=0, 1, …,N)为对应变量的最小和最大时滞.

若模型输入不考虑变量y的前期值，则将式(6)简化为

(7)

优化SVR模型的输入输出结构，即是要确定对目标变量预测有重要作用的关联要素及其时滞.在目标变量关联要素众多、各要素时滞不同且变化范围较大时，潜在可行的模型输入变量及时滞组合极多，从中选择最优组合比较困难.鉴于基于种群的进化算法可很好地应对高维搜索空间，文中河湖水位SVR模型结构优化将基于进化算法开展.另一方面，为保证输入变量及时滞组合对应的预测能力得以准确体现，在结构优化的同时对模型参数也进行同步优化.为避免模型出现过拟合问题，SVR模型训练采用n折交叉验证方式.基于进化算法的SVR模型结构-参数同步优化方法中，种群染色体适应度评估流程见图1.

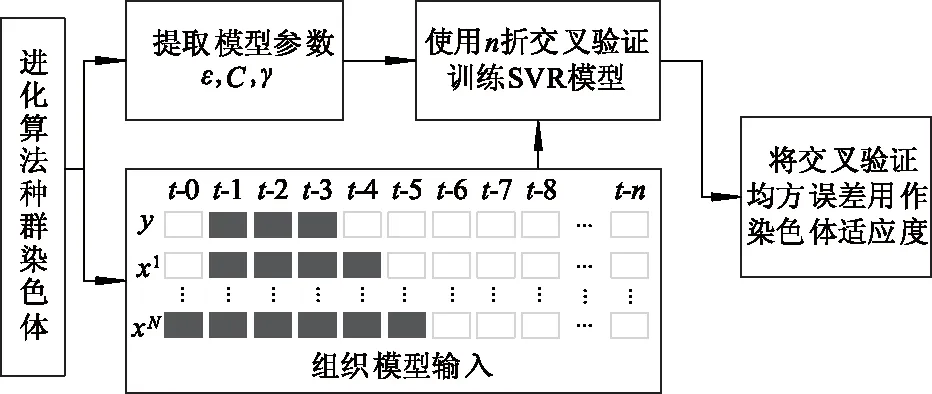
图1 SVR模型结构-参数同步优化中染色体的评估流程

由图1可知，SVR完全嵌入了结构-参数同步优化流程，因此该方法属于基于模型的IVS方法.对于常规的仅支持浮点数编码的进化算法，SVR模型结构-参数同步优化中染色体评估按以下步骤执行：① 将染色体分为2个部分，一部分提供变量时滞信息，另一部分提供模型参数；② 将指示每个变量时滞的2个浮点数向上取整以获取该变量的最大最小时滞；根据所有变量的最大最小时滞信息组织模型输入；③ 使用n折交叉验证训练SVR模型；④ 将交叉验证均方误差用作所评估染色体的适应度.

需要特别说明的是，进化算法中变量时滞的搜索范围需设为略大于其合理范围.在步骤②的取整操作后，若变量时滞超出其合理范围则在组织模型输入时彻底舍弃该变量.这种设定可灵活放弃对目标变量预测作用不大的关联变量.

文中SVR模型结构-参数同步优化方法具有以下特点：① 在SVR模型结构确定过程中同步优化模型参数，可准确反映候选变量及时滞的真实预测能力，有助于发掘SVR的应用潜力；② 模型训练采用了n折交叉验证，有利于避免过拟合问题；③ 所提方法中进化算法的引入，可帮助应对复杂水系考虑关联要素时滞后输入变量搜索空间的高维特性.

1.3 研究数据

为构建洞庭湖城陵矶(七里山)站水位SVR模型，收集了2014—2017年城陵矶站逐日平均水位、洞庭湖四水(湘江湘潭站、资水桃江站、沅水桃源站和澧水石门站)以及长江宜昌站逐日平均流量数据；为构建荆江陈二口站水位SVR模型，收集了2014—2017年陈二口站、上游枝城站、下游马家店站的逐日平均水位，以及同期松滋河新江口站和沙道观站逐日平均流量数据.

2 结果与讨论

基于文中提出的结构-参数同步优化方法，构建了洞庭湖城陵矶水位SVR模型和荆江陈二口水位SVR模型.文中介绍2个模型的构建过程、模型结构参数及模型精度，从而验证论文提出方法的有效性.

2.1 洞庭湖城陵矶水位SVR模型

2.1.1 模型输入输出结构

洞庭湖城陵矶水位SVR模型的输入为考虑时滞的长江和四水流量，以及城陵矶前期水位.由于城陵矶水位同时受长江和四水来水影响，且两者时滞年内和年际波动较大，因此在模型输入中考虑自身站位的前期水位有望大幅提升模型预测能力.

通过SVR构建的城陵矶逐日水位与其影响因素间的映射可表示为

(8)

式中：Lclj为城陵矶逐日平均水位；Di(i=1,…,5)分别为湘江湘潭、资水桃江、沅水桃源、澧水石门以及长江宜昌逐日平均流量.各变量时滞mi和ni(i=0, 1, …,5)单位为d，其最小容许值均为1 d.

2.1.2 模型结构-参数同步优化

文中使用2016—2017年相关数据优化城陵矶水位SVR模型的结构和参数并最终训练模型，而2014—2015年数据则用于模型验证.其中，训练数据中城陵矶水位最高值稍大于验证数据，从而保证模型的泛化能力.使用遗传算法进行城陵矶水位SVR模型的结构和参数优化.遗传算法参数设置：浮点数编码；最大进化代数300，种群规模300；参数ε,C,γ搜索下边界1.0×10-6、上边界1.0×106；变量时滞搜索下边界-0.5、上边界11，若变量时滞取整得到0，则在组织模型输入时舍弃对应变量；所有模型输入都线性归一化至[0, 1]区间，确保各个输入在模型训练时具有一致权重；模型结构-参数同步优化统一采用5折交叉验证的训练方式.

优化程序执行完毕后，得出城陵矶水位SVR模型参数值ε=0.006 8，C=33 026.465 2，γ=0.002 1，选中的模型输入变量时滞见图2(灰色色块).对选中的变量时滞进行了敏感性分析：① 基于模型训练数据，将每个时滞对应的输入数据改变±10%而其余输入保持不变；② 计算2种输入对应水位预测结果的差异的绝对值；③ 取差异绝对值的中位数作为该时滞对水位变化的影响强度；④ 将所有时滞的影响强度一起排序，图2中色块越黑意味着该时滞的影响强度越大.

图2 城陵矶水位SVR模型输入变量时滞

由图2可知，对城陵矶水位预测影响最大的模型输入为同站点前期水位，且前1天至前5天水位信息的影响强度逐步弱化.由于河流流量存在自相关性，图2中各条河流流量时滞近似还原了水流运动时间，而敏感性分析结果恰当地反映了不同河流对城陵矶水位变化影响的差异性.长江来水对位处洞庭湖与荆江交汇处的城陵矶水位有着最为显著的影响，且由于长江流量年内波动大，其时滞变化范围在所有河流中也最大.洞庭湖四水中，湘江影响最强，澧水影响最弱，资水、沅水介于二者之间.

2.1.3 模型精度评估

文中采用多重指标对构建的城陵矶水位SVR模型进行精度评估，指标包括均方根误差(RMSE)、决定系数(R2)和平均绝对误差(MAE).

训练期和验证期的城陵矶水位SVR模型精度评估结果见表1，城陵矶水位预测值与实测值对比见图3.

由表1可知，2个时段模型RMSE均小于0.060 m，R2均大于0.999 0，MAE均小于0.040 m，取得了理想的模拟预测精度.模型在训练期和验证期的精度差异很小，未出现过拟合问题，证明模型结构-参数同步优化采用的5折交叉验证发挥了预期作用.从图3可以看出，2个时段的水位预测值与实测值吻合较好，特别是在验证期高水位时，模型精度没有下降，这一结果可归因于模型在训练期有机会学习更严重的洪水情景.训练期和验证期模型的最大高估误差分别为0.17 m和0.29 m，而最大低估误差分别为-0.32 m和-0.29 m.在训练期和验证期，分别有96.3%和94.2%的水位预测误差绝对值不超过0.10 m.

表1 城陵矶水位SVR模型精度评估结果

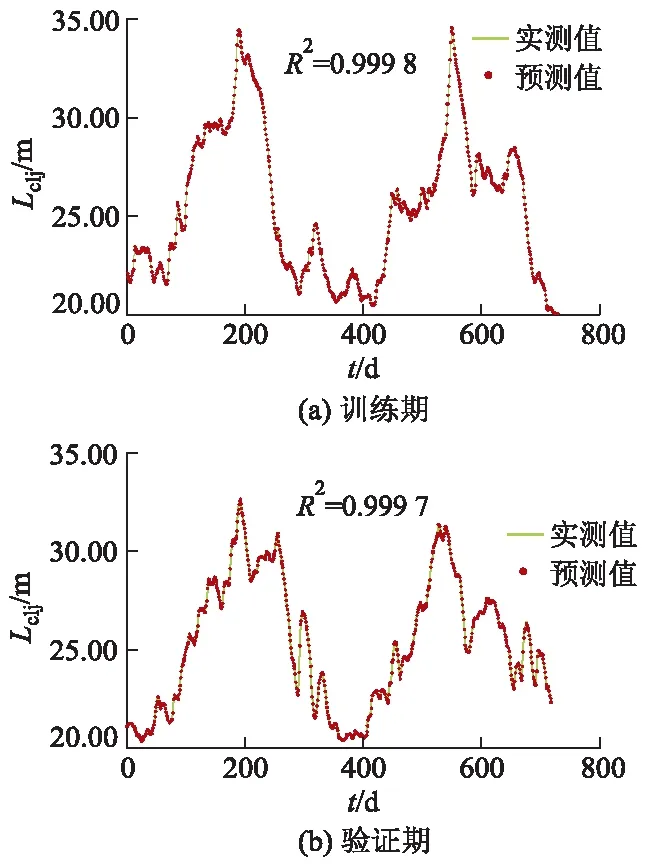
图3 城陵矶水位预测值与实测值对比图

2.2 荆江陈二口水位SVR模型

陈二口水位连续监测开始时间较晚，当前有向历史年份外延陈二口水位数据的实际需求.文中拟基于陈二口上、下游临近站点的水位和流量信息构建陈二口水位SVR模型，因此输入变量不考虑自身站位的前期水位.

2.2.1 模型输入输出结构

荆江陈二口水位SVR模型的输入为考虑时滞的枝城站和马家店水位，以及松滋河新江口和沙道观流量.

通过SVR构建的陈二口逐日水位与其影响因素间的映射可表示为

(9)

式中：Lcek为陈二口水位；L1和L2分别为枝城站水位和马家店水位；D1和D2分别为新江口流量和沙道观流量.各变量时滞mi和ni，i= 1, 2, …, 4,单位为d，其最小容许值均为0.

2.2.2 模型结构-参数同步优化

为实现陈二口水位序列向历史年份外延，文中使用2014—2016年相关数据优化陈二口水位SVR模型的结构和参数并最终训练模型，2017年数据则用于模型验证.陈二口水位一般低于枝城站水位、高于马家店水位，且更接近后者.然而，枯水期陈二口水位与马家店水位差异显著，进入汛期后两者差异变小，因此简单地考虑站点间距进行陈二口水位插值难以获得准确结果.

陈二口水位SVR模型结构和参数优化中，遗传算法设置与2.1.2节类似.优化得到的陈二口水位SVR模型参数值ε= 0.095 8，C=274 302.672 1，γ=0.000 1，选中的模型输入变量时滞见图4.对选中的变量时滞进行了敏感性分析，方法与2.1.2节类似.

图4 陈二口水位SVR模型输入变量时滞

由图4可知，对陈二口水位预测作用最大的变量为枝城站和马家店水位.对于td陈二口水位预测，上述站点td水位的作用明显大于t-1 d水位，这与3个站点距离较近有关(枝城站至马家店距离不超过35 km).此外，新江口流量(t和t-1 d)和沙道观流量(td)也被选入模型输入，说明松滋河流量对陈二口水位的预测发挥了积极的辅助作用.

2.2.3 模型精度评估

陈二口水位SVR模型的精度评估仍然基于RMSE,R2和MAE，评估结果见表2，陈二口水位预测值与实测值对比见图5.表2中2个时段模型RMSE均小于0.070 m，R2均大于0.998 0，MAE均小于0.050 m，说明优化后模型取得了理想的模拟预测精度.模型训练期和验证期的精度未出现过大差异，不存在过拟合问题.由图5可知，2个时段的水位预测值与实测值均可较好吻合，偏离理想线的情况极少.训练期和验证期模型的最大高估误差分别为0.15 m和0.20 m，最大低估误差分别为-0.15 m(但存在一个异常点：-1.03 m)和-0.18 m，最大低估幅度与最大高估幅度非常接近，说明模型没有出现系统性偏差.

表2 陈二口水位SVR模型精度评估结果

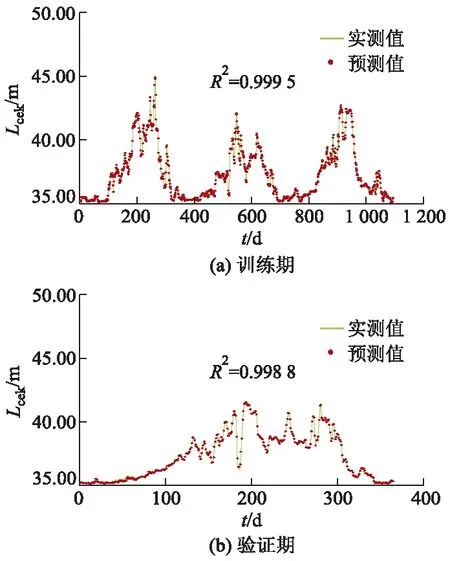
图5 陈二口水位预测值与实测值对比

3 结 论

1) 基于结构-参数同步优化的水位预测模型可准确反映不同影响因素对水位预测的作用大小，城陵矶水位预测最主要的外部因素为长江来水和湘江来水，陈二口水位预测则为枝城站和马家店水位.

2) 结构-参数同步优化可充分发掘SVR潜力，城陵矶水位模型(RMSE<0.060 m，R2>0.999 0，MAE<0.040 m)和陈二口水位模型(RMSE<0.070 m，R2>0.998 0，MAE<0.050 m)均取得了理想精度.

3) 提出方法不仅能实现较高的模型精度，其采用的n折交叉验证方式还可有效避免模型过拟合问题，构建的水位预测模型在训练和验证期的精度差异不明显.