车用凸轮式氢气循环泵内非定常流动特性
2022-05-25董亮张立新刘厚林朱建成
董亮,张立新,刘厚林,朱建成
(江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013)
随着世界各国陆续公布传统内燃机汽车的禁售时间,氢燃料电池汽车成为各大汽车厂商研究的热点[1-2].质子交换膜燃料电池由于能够在比较适宜的温度下运行,被认为是陆上交通动力的首要选择[3-5].质子交换膜燃料电池系统主要包含空气供应子系统、氢气循环子系统和水热管理子系统等.其中,氢气循环子系统向电堆连续提供一定压力和流量的高纯度氢气,保证燃料电池电堆中的电化学反应正常进行.同时,电堆出口的氢气带有一部分水汽,通过循环进入电堆阳极进口,以保证燃料电池内的水平衡.氢气循环子系统对整个系统的动力性、经济性以及电堆内部水平衡和膜电极寿命都起到至关重要的作用[6-8].
质子交换膜燃料电池阳极氢气循环系统主要有2种工作模式:一种是通过氢气循环泵将未反应的氢气循环回电堆阳极进口,另一种是通过引射器引射未反应的氢气进入电堆阳极进口.引射器存在小功率工况下无法工作、控制困难以及电堆内部反应不均匀等问题,而氢气循环泵具有工作范围广、控制简单、电堆内部反应均匀等优点[9-10].
目前,氢气循环泵主要依赖进口,国外主要有日本丰田自动织机研发的二叶直根型凸轮式氢气循环泵和德国Busch研发的爪式氢气循环泵.随着燃料电池技术的日益成熟,各大汽车厂商相继推出自己的氢燃料电池汽车.搭载氢气循环泵的新能源汽车在运行中存在水汽冲击、低温启动难、噪声高等问题,如何进一步提高氢气循环泵效率、减振降噪、延长使用寿命,是其大规模产业化的技术瓶颈.
文中以某一种车用凸轮式氢气循环泵为研究对象,对高转速工况下泵内部流场进行非定常数值模拟,分析泵内部流场分布规律和压力脉动特性,探究氢气循环泵内部不稳定流动产生的机理,为进一步研究凸轮式氢气循环泵内流脉动特性提供一定参考.
1 三维建模及网格划分
1.1 计算模型
文中研究的凸轮式氢气循环泵结构上属于回转式容积泵,主要由前盖板、泵体、齿轮、凸轮转子、后盖板、轴承、主动轴及从动轴等组成.采用三维造型软件UG对其进行建模,如图1所示.
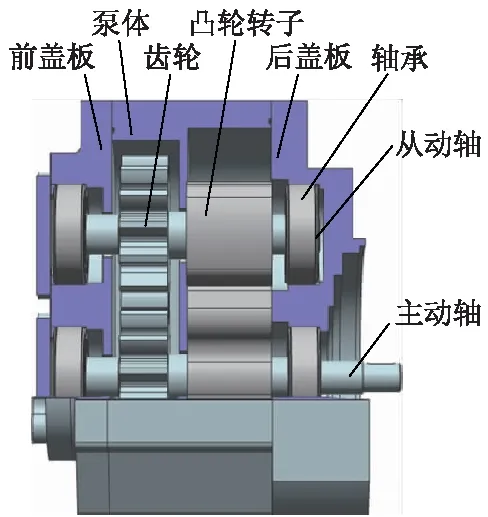
图1 凸轮式氢气循环泵三维模型
凸轮式氢气循环泵基本参数分别为进出口直径d=20 mm,节圆半径Rp=30 mm,外圆半径Rm=44 mm,径距比1.47,转子间隙δL=0.18 mm,转子与泵腔壁面间隙δr=0.25 mm,轴向间隙δa=0.02 mm,面积利用系数λ=0.49,额定转速n=8 000 r/min. 根据燃料电池汽车的研究报告,车用氢气循环泵的升压比γ应为1.2~1.6[11],文中设定γ=1.2.
将凸轮式氢气循环泵流动区域划分为3个部分,分别为吸气流道、泵腔旋转流道和排气流道.为了使介质均匀进入泵腔,减小介质紊流对监测结果的影响,对进出口流道适当延长,延长距离为3~5倍管径,文中设定进出口流道延长距离为3倍管径.计算模型如图2所示,内流分析时,转子转动以图中所在位置0°初始位置为基准.

图2 计算模型
1.2 网格划分及其无关性验证
采用ICEM-CFD软件对氢气循环泵内部流道进行网格划分,其中进出口流道采用结构化网格,泵腔区域采用棱柱网格.
瞬态数值模拟中,为保证模拟精度,需要对网格进行无关性验证.绘制4套网格,以排气流量Q为监测量,分别计算网格数N对模拟精度的影响,如图3所示.

图3 网格无关性验证
由图3可以看出,网格数为350万和400万的排气流量误差为0.16%,可以认为350万的网格数已经满足模拟精度要求,同时考虑计算时间和计算机配置,最终选取模拟网格数为350万.
2 数值计算
2.1 边界条件设置
工作介质设置为氢气,采用Realizablek-ε湍流模型.固体壁面设置为无滑移壁面,靠近泵腔壁面处的流动采用标准壁面函数处理.氢气循环泵进口设置为压力进口,p=110 kPa,进气温度设为280 K.氢气循环泵出口设置为压力出口,p=132 kPa,排气温度设为300 K.湍流强度为5%,水力直径为0.02 m.进出口流道与泵腔连接面采用“interface”类型进行交界面网格连接,其余壁面均设置为“wall”.通过UDF宏DEFINE_CG_MOTION定义凸轮转子的旋转运动,凸轮外表面设置为刚体“rigid body”,泵腔上下表面设置为变形区域“deforming”,采用弹簧近似光滑模型和局部重构模型对网格进行调整.求解器算法采用PISO的压力-速度耦合算法进行求解,时间步长设置为2.0×10-6s.PISO算法是压力的隐式算子分割算法,是处理非稳态可压流动问题的压力-速度计算程序,对于瞬态问题具有明显优势[12-13].
2.2 计算流体力学控制方程
为了使数值模拟的结果贴近工程实际运行工况,需对计算流场建立合理的数学模型.车用凸轮式氢气循环泵内流场工作介质为可压缩的气态氢气,因此计算流体力学控制方程包括质量守恒方程、动量守恒方程、能量守恒方程和气体状态方程[14],其形式分别为

(1)
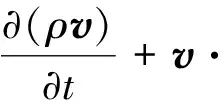
(2)
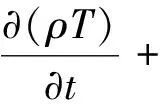
(3)
(4)
上述式中:ρ为流体密度;t为时间;v为速度矢量;f为质量力;p为流体压力;μ为动力黏度;T为流体温度;k为流体的传热系数;Cp为等压比热容;ST为黏性耗散项;R为摩尔气体常数;M为气体摩尔质量.
Realizablek-ε模型是一种高雷诺数湍流模型,由于模型中引入了与旋转和曲率有关的系数Cμ,使得它在求解旋转流动、流动分离以及复杂的二次流都有更加精确的结果[15].Realizablek-ε模型的湍流输运方程可表示为
(5)
(6)
(7)
上述式中:vt为涡黏性系数;k为湍动能;ε为湍流耗散率;σk为湍动能k的湍流普朗特数;σε为耗散率ε的湍流普朗特数.
3 数值模拟结果及分析
3.1 内流场分析
图4为凸轮式氢气循环泵在1个周期内不同转动角度下内部流场压力等值线分布,可以看出:凸轮转子转过18°时,进气腔容积逐渐增大,排气腔容积逐渐减小,排气腔内气体被压缩,压力逐渐升高;凸轮转子转过54°时,基元容积与排气腔连通,排气腔内高压气体通过缝隙回流到基元容积,导致基元容积内气体压力突然升高;凸轮转子转过90°时,基元容积内的气体被推移到排气腔,凸轮转子与下侧壁面形成新的基元容积;凸轮转子转过108°时,排气腔内气体继续被压缩;凸轮转子转过144°时,下侧基元容积与排气口连通,新的基元容积内的气体也被输送到排气口.综上分析,上下2个凸轮转子旋转180°,氢气循环泵吸气、排气各1次.

图4 不同转动角度下的静压分布
图5为凸轮式氢气循环泵在1个周期内不同转动角度下流道速度分布,可以看出:凸轮转子啮合区域及凸轮转子与泵腔壁面间隙处均出现较大气体流速,这主要是由转子旋转过程中挤压气体形成高速区所致;凸轮转子转过18°时,进气腔容积逐渐增大,在进口处形成低压区产生旋涡;随着转子转动角度增大,进气口处的旋涡逐渐变大并随着转子顺时针方向移动;凸轮转子转过108°时,排气流道内高压气体回流,与出流气体混合形成冲击旋涡;凸轮转子转过144°时,随着下侧基元容积与排气腔连通,排气腔气体压力升高,回流气体和出流气体混合形成较小的旋涡,同时,进气腔内出现新的旋涡;凸轮转子转过180°时,随着排气腔内气体被进一步压缩,出流气体占据排气流道,且进气口旋涡逐渐变大.

图5 不同转动角度下的速度分布
图6为凸轮式氢气循环泵在1个周期内不同转动角度下流道内温度分布云,可以看出:凸轮转子转过18°时,进气流道内转子和机壳间隙处以及转子啮合处气体温度出现了小幅度升高,这是由于基元容积与排气腔连通时,排气腔内高压气体通过间隙回流出现了温度扩散现象;随着转子转动角度增大,排气腔内气体逐渐被压缩,排气腔内气体温度开始升高,并开始向排气口扩散.

图6 不同转动角度下的温度分布
通过对流道内压力场和速度场分布的分析,从宏观上了解了氢气循环泵的内部流态,但是不能得到凸轮转子和氢气之间的能量交换关系.文中采用涡动力分析方法[16],通过分析不同转动角度下排气流道内涡量分布,得到氢气循环泵出口回流的演变情况.
图7为凸轮式氢气循环泵在1个周期内不同转动角度下流道内涡量分布,可以看出:凸轮转子转过18°~90°时,进气腔内主要是正的z向涡量,并随着转子转动角度的增大而增大,而排气流道内主要是负的z向涡量,并随着转子转动角度的增大而减小,这主要是由于基元容积与排气腔连通,排气腔内高压气体通过间隙回流,所以随着转子角度增大,排气腔气体被压缩,回流现象减弱,因此负的z向涡量减小;凸轮转子转过108°~180°时,随着转子转动角度增大,进气腔内负的z向涡量增大,排气腔内正的z向涡量增大并占据排气流道,这主要是由于进气腔容积增大在进气口形成低压区,产生旋涡,但随着排气腔内气体被进一步压缩,排气流道内主要是出流气体,回流现象消失,这与前述速度分布的分析结果相一致.

图7 不同转动角度下的涡量分布
3.2 流量脉动特性分析
凸轮式氢气循环泵在运行中,进气腔和排气腔容积发生周期性变化,导致流量也出现周期性脉动.为了分析泵的流量脉动特性,在泵出口设置监测点观察泵出口流量的变化情况,并将数值模拟流量和理论分析流量进行对比,以得到泵流量随凸轮转子转动角度变化的脉动特性.
假设不考虑压缩和泄漏等因素的影响,氢气循环泵在单位时间内输送的气体容积称为理论流量.理论流量是泵运行1个周期内的流量平均值[17],即
(8)
式中:Qth为理论流量;D为叶轮外径;L为叶轮长度;n为泵转速;λ为叶轮面积利用系数.
根据式(8)进行计算,得到本次分析的氢气循环泵理论流量为101.09 m3/h.
氢气循环泵叶轮之间以及叶轮与壳体间均存在间隙,在排气过程中,排气压力高于进气压力,部分气体通过间隙回流到进气腔体,称为内泄漏.气体通过轴端间隙的泄漏称为外泄漏,一般气体的外泄漏量较小,可以忽略不计.
根据亚临界内泄漏流量的经验公式[18],计算沿叶轮长度方向的泄漏量为
(9)
式中:δ为叶轮间的间隙或叶轮与壳体间的间隙;Δp为压升;ρs为进口气体密度.
式(9)代入叶轮间的间隙δL值进行计算,得到叶轮间的泄漏量QbL=14.67 m3/h;代入叶轮与壳体间的间隙δr值进行计算,得到叶轮与壳体间的泄漏量Qbr=20.38 m3/h.
高效解法:(xe2x- lnx-1)/x=(e2x+lnx- lnx-1)/x≥[(2x+lnx+1)-lnx-1]/ x=2,当且仅当2x+lnx=0时取等号,∴a≤2。
沿叶轮端面间隙的泄漏量为
(10)
式中:τ为系数,τ≈1/50;b为叶轮端面的平均宽度,b≈0.5π(1-λ)D/Z.代入式(10)进行计算,得到叶轮端面间隙的泄漏量Qb=0.67 m3/h.
综上,氢气循环泵实际流量为
QB=Qth-QbL-Qbr-Qb,
(11)
分别代入各数值进行计算,得到氢气循环泵理论分析排气流量为65.37 m3/h.
图8为凸轮式氢气循环泵在1个周期内进气和排气流量曲线,可以看出:氢气循环泵运转1个周期,流量产生4次脉动,即流量函数具有π/Z的脉动周期;由排气流量脉动曲线可知,在1个旋转周期内共出现4次流量脉动,并且流量脉动均出现了4个峰值,这主要是由于在1个旋转周期内排气口共出现4次回流,回流气体与排气混合导致出现多个峰值.数值模拟得到的排气流量平均值和理论分析结果误差为4.7%,表明基于动网格技术的数值模拟能较准确地预测凸轮式氢气循环泵内流脉动特性.

图8 流量脉动曲线
3.3 压力脉动特性分析
凸轮式氢气循环泵主轴转频为133 Hz,旋转基频为267 Hz.为了分析氢气循环泵旋转流道内周向流体的压力脉动,在旋转流道周向设置压力监测点,监测点位置如图9所示.

图9 压力监测点分布
3.3.1 压力脉动时域特性
选取氢气循环泵稳定运行时2个旋转周期内的压力脉动时域数据进行分析,结果如图10所示,可以看出,旋转流道内各监测点处压力均呈现周期性变化规律,在1个旋转周期内,共出现2次压力脉动,并且每次压力脉动均出现多个峰值.这主要是由于在1个旋转周期内,凸轮转子扫过2次旋转流道壳体,二者动静干涉引起的压力脉动,同时由于回流影响,每次流量脉动产生4个峰值,而流量脉动作用于介质产生压力脉动,导致压力脉动也呈现多峰值特征.

图10 旋转流道各监测点压力脉动时域特性
3.3.2 压力脉动频域特性
为了分析氢气循环泵凸轮转子和旋转流道壳体间由于动静干涉引起的压力脉动频率分布规律,应用FFT技术将各个监测点上的压力脉动时域信息转化为频域信息.图11为凸轮式氢气循环泵稳定运行1个周期内各监测点处压力脉动的频域分布,可以看出,旋转流道周向各监测点的压力脉动主频为267 Hz,与氢气循环泵转子旋转基频一致,这进一步表明压力脉动主要是由凸轮转子和旋转流道壳体间动静干涉引起的.
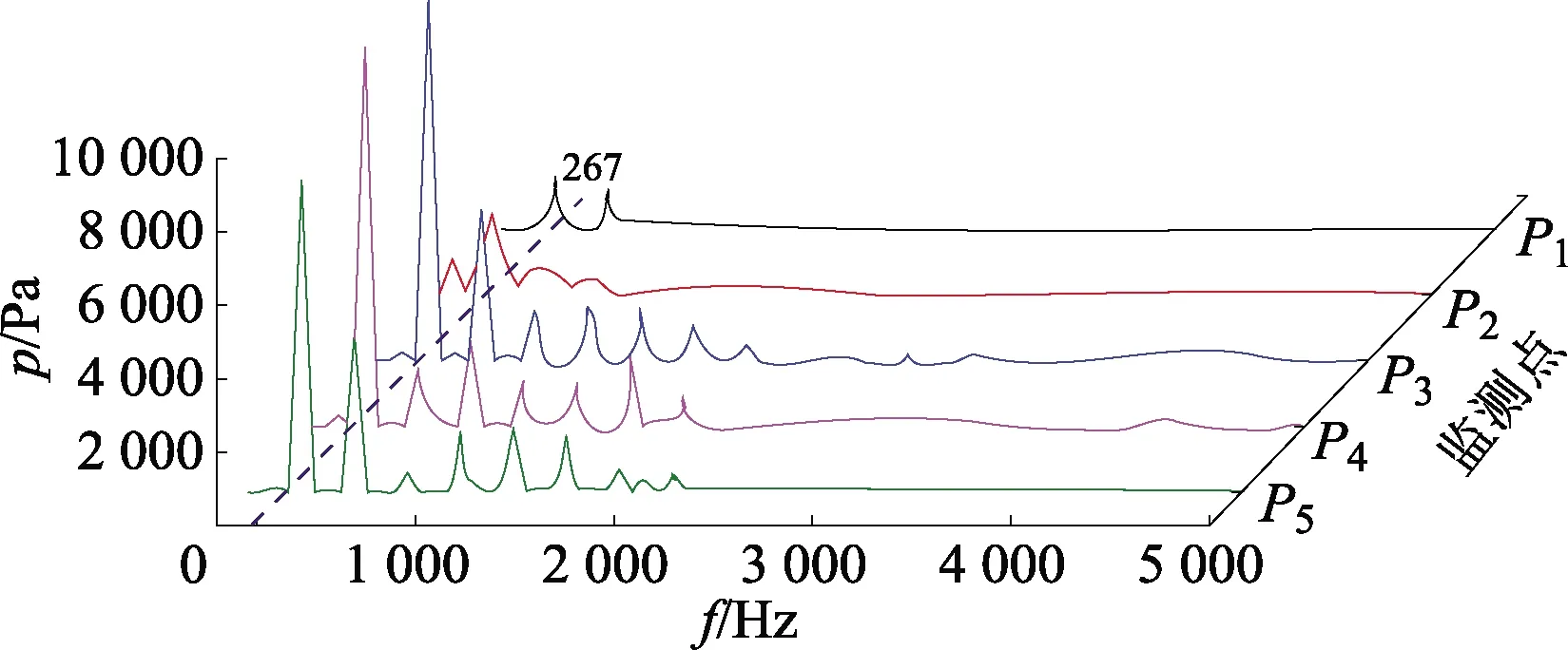
图11 旋转流道各监测点的压力脉动频域特性
4 结 论
1) 基于ANSYS Fluent软件的动网格技术,采用Realizablek-ε湍流模型和PISO压力-速度耦合算法,对氢气循环泵全流道进行非定常可压缩数值模拟,数值模拟获得的排气流量平均值和理论分析结果误差为4.7%,可以较准确地反映泵内部气体流量脉动规律.
2) 分析排气流道内涡量分布规律,表明排气流道内出口回流和负的z向涡量分布区域相重合,随着出流气体占据排气流道,负的z向涡量消失,流态变得平稳.
3) 凸轮式氢气循环泵旋转流道周向压力脉动主频为267 Hz,与转子旋转基频一致,表明压力脉动主要是由凸轮转子和旋转流道壳体间动静干涉引起的.
