湿度场下膨胀岩巷道围岩变形数值模拟分析
2022-05-25梁向东袁兆廷刘长红欧阳保
梁向东,袁兆廷,刘长红,欧阳保
(中铁二十四局集团南昌铁路工程有限公司,江西 南昌 330002)
0 前 言
膨胀岩属于软岩,是指在水的物理、化学等作用下易于发生体积膨胀、强度软化,整体性发生碎裂和分解的一种比较特殊的岩石[1]。对于巷道围岩变形破坏规律现已有较多研究[2-3],膨胀岩围岩在高湿度环境下变形速度增快、延性增大。因此,在膨胀性岩体中开挖巷道、硐室时,在水的作用下围岩易发生膨胀变形、强度降低等情况危害工程安全[4]。除膨胀岩自身所具有的胀缩、崩解和软化等内在特性外[5],围岩的膨胀进一步会导致支护结构的变形,甚至产生弯矩。在加以施工扰动、围岩应力和设计因素的共同影响所造成的工程事故为其外在因素。因此,在实际工程中选取合理的控制方法保障膨胀岩巷道施工安全具有重要意义[6-7]。文章以实际问题为研究点,在高湿环境且具有膨胀性巷道环境下,计算分析采用正交设计方案,并利用数值模拟研究围岩膨胀性、衬砌等若干因素对巷道围岩变形的影响。
1 正交数值模拟试验
1.1 计算方案选取
本实验选取正交试验法进行数值模拟。主要针对围岩巷道膨胀性、有无衬砌和埋深的影响,制定出数值模拟方案表见表1。
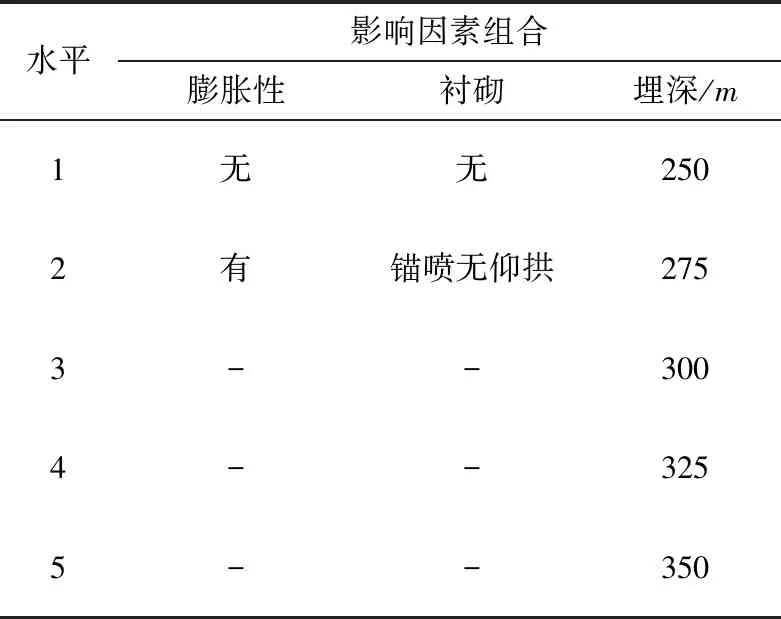
表1 数值模拟影响因素表
依靠相关条件吻合度及研究目的,并考虑相关因素及影响水平程度。通过混合水平正交试验表确定如表2所示的具有代表性的数值模拟计算分析方案。通过系统地研究上述因素对膨胀岩巷道围岩变形的影响,为工程实际提出合理建议。
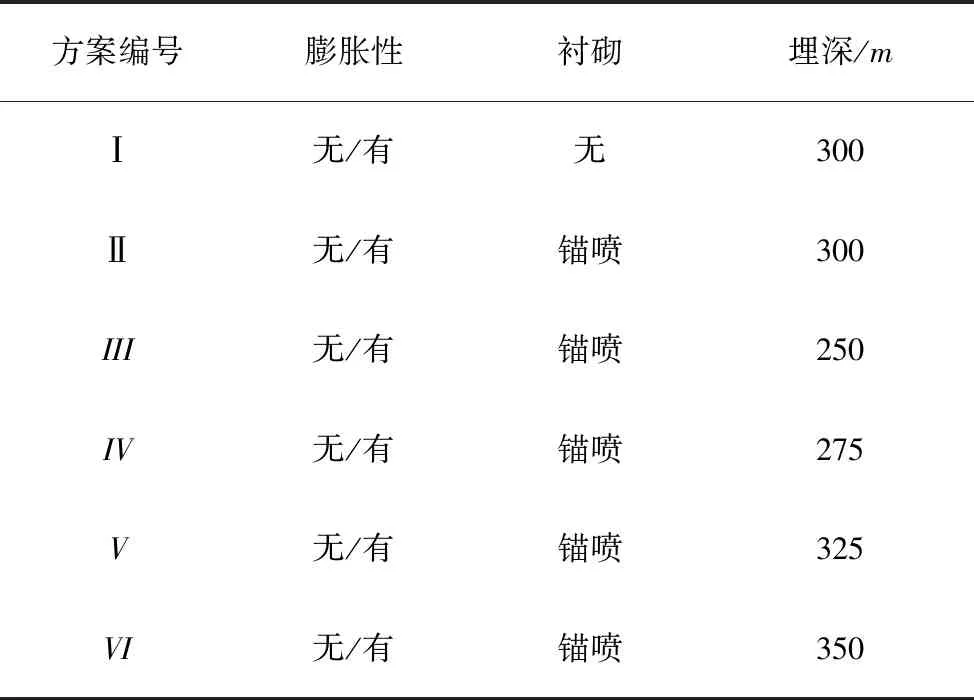
表2 数值模拟试验表
1.2 计算模型与参数
本实验选取模型参数易获取且较好模拟膨胀岩的变形特性,同时又适用于膨胀岩材料的D-P弹塑性本构模型。ABAQUS中D-P弹塑性本构模型模拟膨胀岩材料物理力学参数由前期试验并将试验数据和《膨胀岩与工程》对照综合得出。依据表面浸润和膨胀力试验,并结合数值计算反演确定导热系数λ和热膨胀系数β。通过缪协兴的湿度应力场的控制微分方程及基本原理,在利用有限元模拟软件可将温度场参数β,T转化成湿度场参数α,W使用ABAQUS进行有限元计算,取α:β≈100,即设温度T为0℃时对应含水量W为0,及膨胀岩处于干燥状态,设温度T为100℃时对应含水量W为1,及膨胀岩处于饱和含水状态,T与W一一对应,并使温度T每增加1℃对应湿度W增加1%。
1.3 ABAQUS建模
根据相似模型试验,获取湿度分布特性以及综合考虑实际状况下膨胀岩巷道中受施工用水与凿岩积水等因素影响,绘制出含水量等值线图,根据参数设定,利用ABAQUS软件中的温度单元模拟上述条件下的膨胀岩水分分布,最终获得温度分布云图。
1.3.1 模型单元类型选择和网格划分
使用ABAQUS对围岩进行二维建模,创建膨胀岩围岩部件,在热分析材料属性值输入密度、导热系数、热膨胀系数和比热容等参数,分析步类型选择“热传递”,基本信息选择“稳态热分析”,单元类型为四边形单元DC2D4,传热方式为四结点线性传热,对巷道两侧围岩采用四结构化网络划分技术进行阶梯状均匀递增划分,对围岩和中心巷道采用中性轴算法划分网格,最终划分出的单元总数为8 452个。
1.3.2 边界条件选取
首先建立一个预定义场,选择15℃为围岩的初始温度,通过有限元软件换算即围岩初始含水量为15%。在巷道中间正下方1m处的围岩输入35℃的热源作为初始水源向周围扩散,达到水分迁移效果,并在巷道顶部向上2.5m处施加边界条件以阻隔热量持续向周围扩散,完成上述边界条件的设定。根据本文依托的基金项目在前期展开试验研究所发表的成果,施加的湿度场如图1所示。
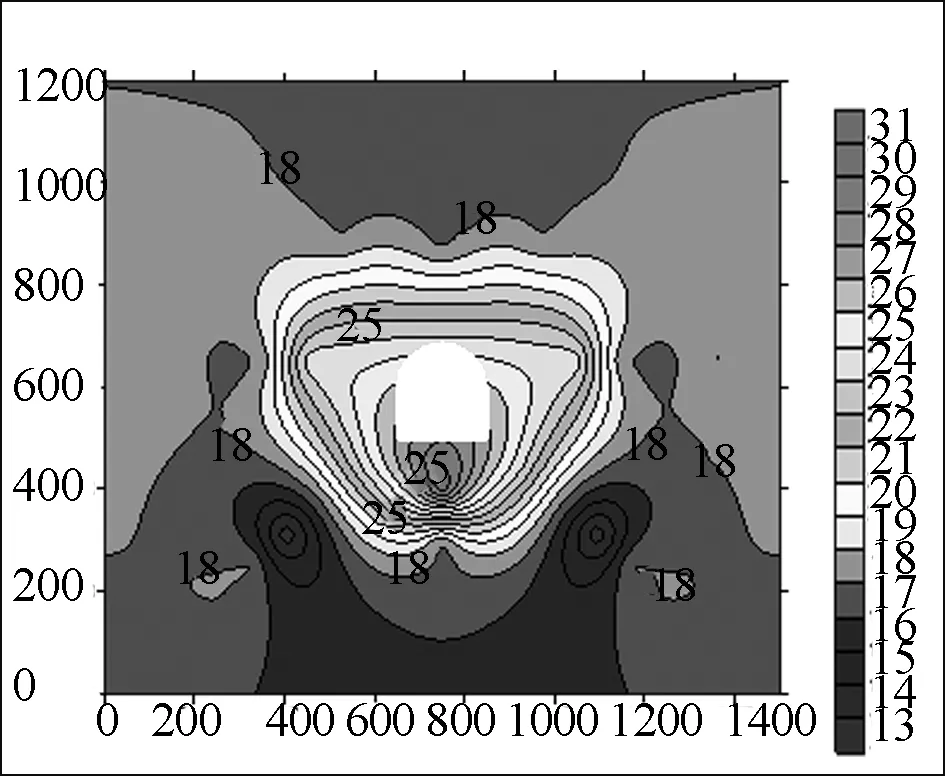
图1 围岩含水量等值线图(单位:mm)
2 数值模拟试验结果分析
2.1 膨胀性和衬砌对巷道围岩变形的影响分析
通过对比计算方案Ⅰ与Ⅱ的结果,根据顶板沉降量Uy以及底板鼓起量Uf的大小,研究有支护结构条件下以及围岩有无膨胀性条件下交叉的四种情形对巷道变形的影响;其计算结果如图2~3所示。
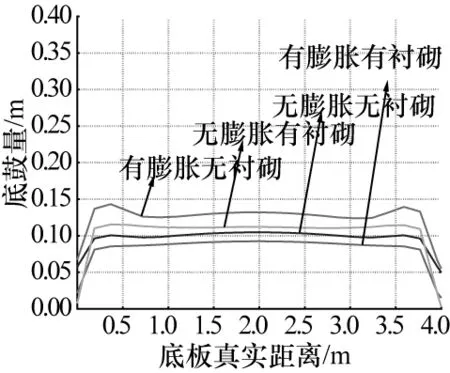
图2 底板鼓起变形量
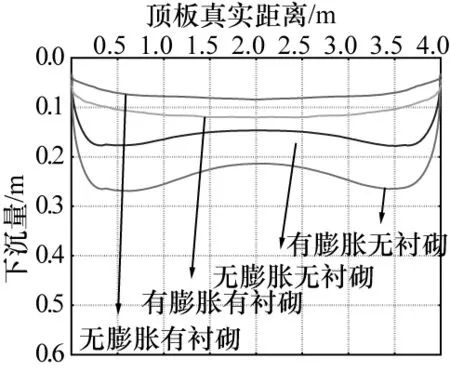
图3 顶板下沉变形量
由图2~3知,在无膨胀性围岩情形下的巷道,衬砌对限制巷道顶板及底板两侧变形有较明显的抑制效果。由图可以看出,在相同工况下,顶板的变形量均要大于底板的变形量,因此,在实际工程中要加强对顶板的沉降监测,以保证施工安全,无衬砌顶板变形最大值出现在靠近边墙两侧附近;对于膨胀性巷道而言,衬砌结构可以将无支护的围岩底板鼓起量和顶板下沉量分别减少149mm和28mm。可见衬砌对顶板下沉的抑制作用比较大,同时衬砌相比膨胀岩具有更好地抑制围岩变形的效果,同时也说明膨胀性对巷道开挖的危害较大。
2.2 埋深对围岩变形的影响分析
本研究通过对顶板和底板两个位置的变形情况为例探究在膨胀性巷道中埋深对围岩变形的影响。对方案III-VI的数值模拟计算结果如图4~7所示。
由图4~5可知,在该断面形式和地应力条件下的巷道,在底板有膨胀性变形中两侧凸起均比无膨胀性较严重,底板鼓起量随着埋深的增加而逐渐增加。由图6~7可知,顶板的两侧凸起规律与底板相反,呈现出从中间向两侧变形量逐渐递减的规律,其底板变形也是随着埋深的增加而增加。对于无膨胀性巷道而言,相同埋深下底板和顶板变形量相差不大,其底板鼓起量和顶板下沉量的规律是随着埋深每增加25m而增加约8mm。而在有膨胀性巷道中,相同埋深下顶板的变形比底板大,底板下沉量是随着埋深每增加25m而增加23mm,而底板鼓起量趋势等梯度埋深逐渐增大,并且底部靠近两帮附近变形量表现最为突出,可见膨胀性对顶板下沉量和底鼓起量的影响较大。
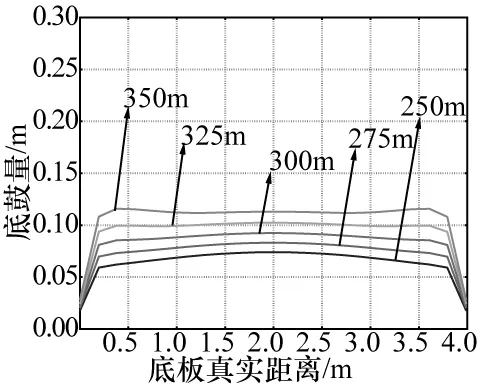
图4 不同埋深无膨胀底板变形量
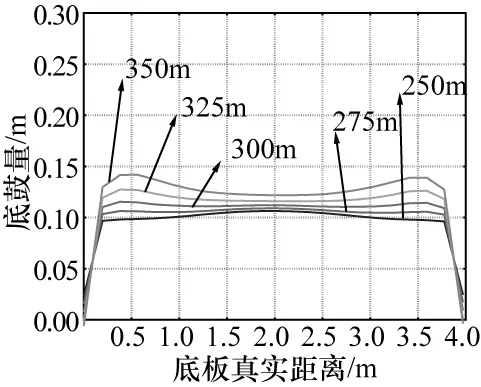
图5 不同埋深有膨胀底板变形量
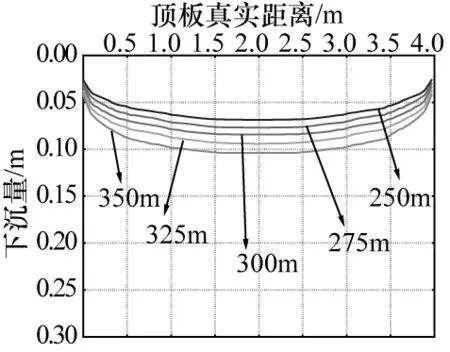
图6 不同埋深无膨胀顶板变形量
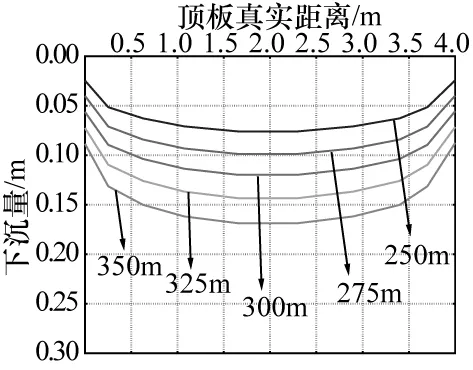
图7 不同埋深有膨胀顶板变形量
3 结 论
1)有无膨胀性和有无衬砌对围岩的变形影响显著,在无衬砌条件下,底板和顶板均出现较大变形,在衬砌作用下,可以明显地抑制围岩变形,特别是对边墙两端的底板隆起量和顶板下沉量作用显著。
2)顶板下沉量和底板鼓起量随着埋深增加而均呈现不同程度的增加,膨胀性对顶板下沉量和底板鼓起量的影响较大。
3)在三种因素中顶板和底板变形量影响程度大小顺序均一致,顶底板移近量因素的程度大小的次序为:埋深<膨胀性<衬砌。
[ID:013219]
