角钢混凝土界面黏结性能研究

李晓霞

(山西省建筑安装技工学校，山西 太原 030006)

0 引言

钢筋混凝土因其具有良好的强度、刚度和稳定性能，在工程中的应用越来越多，而钢筋与混凝土之间的黏结力是这两种材料可以共同的基础，许多研究人员对此做了一系列研究。

李斌等[1]研究了钢筋锈蚀对黏结强度的影响，通过系数试验，分析了钢筋坑蚀深度对黏结强度的影响规律。陈梦成等[2]对目前常用的几种黏结应力计算方法进行了对比，并利用有限元软件进行了理论验证和细致分析。张彤等[3]对混凝土开裂前的黏结力方程进行了推导，并对相关参数进行了敏感性分析。基于此，杨海峰等[4]研究了再生混凝土骨料与钢筋的黏结作用，探究了不同条件下的钢筋混凝土荷载-滑移曲线以及钢筋应变情况。蒋德稳和邱洪兴[5]结合钢筋混凝土实际工作状态，对反复荷载作用下钢筋混凝土的疲劳特性做了研究。洪芳和张铮[6]通过外黏贴对钢筋混凝土结构进行了加固，通过ANSYS软件进行模拟对加固效果进行了评价，结果表明，该加固方法能较好地提高钢筋混凝土界面的黏结强度。

本文采用正交试验，对影响角钢-混凝土界面黏结强度的因素进行了分析，通过极差分析法，确定了各因素对黏结强度的影响效果。利用有限元软件建立了角钢-混凝土三维模型，并利用本文试验结果验证了模型的有效性，对比了与试验结果的差异，对角钢混凝土的破坏形式和黏结强度与滑移量变化关系的不同阶段进行了推导。

1 试验概况

1.1 试件尺寸及性能

参考相关文献以及实际工程应用，试验用到的角钢混凝土试件尺寸设置为150 mm×150 mm×150 mm(长×宽×高)，图1展示了试件的模型简图。为了研究角钢混凝土界面黏结性能的影响因素，对保护层厚度、混凝土强度以及黏结长度进行了正交试验。

选用三种规格的角钢，分别为L40×4，L50×5和L63×6，前者表示等边角钢的肢长，后者表示角钢厚度，单位均为mm。三种角钢对应的保护层厚度分别为46 mm,39 mm和30 mm，保护层厚度规定为角钢边缘与混凝土外边缘距离的最小值。混凝土强度等级选用C30，C40和C50三个等级。黏结长度选用50 mm，100 mm和150 mm。为了便于表示，以角钢型号L40×4、混凝土强度等级C30，黏结长度50 mm为例，试样编号为C30-L40×4-B50。共设置了9组正交试验。

试验用到的角钢力学参数见表1。为了保证在试验时角钢受力均匀，减少试验误差，将角钢的加载端进行磨平处理。表2展示了混凝土的配合比情况。试验选用了3种强度等级的混凝土，在正交试验前参考相关标准，制作了18个标准立方体混凝土试块，表3展示了养护28 d之后的混凝土强度实测值。

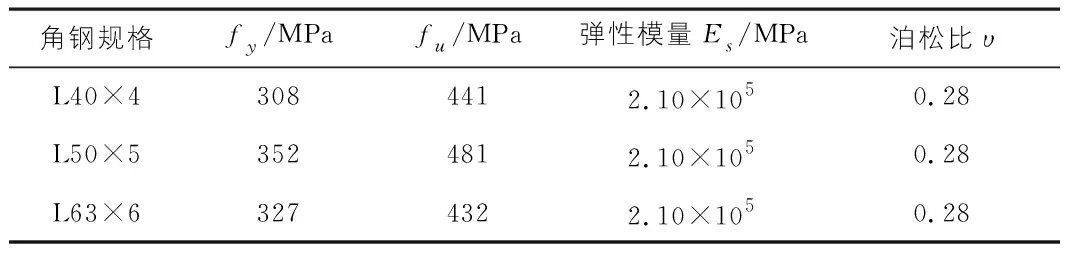
表1 角钢力学指标

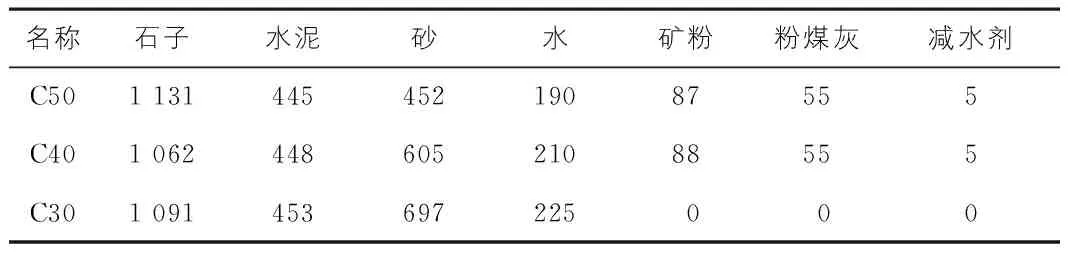
表2 混凝土配合比 kg/m3

表3 混凝土立方体抗压强度 MPa

1.2 加载方式

试验时对角钢上端进行加载，采用1 000 kN的伺服液压机，加载控制方式选择位移控制方式。试验时设置4个位移监测点以测量支座沉降，试件下放置两块环形钢垫块支撑。图2为加载装置简图。

2 试验结果分析

2.1 荷载-滑移曲线

图3展示了角钢混凝土试样的荷载-滑移曲线。从图3中可以看出，随着试验的进行，滑移量逐渐增加，在试验初期，试验施加的荷载随滑移量S的增加而增大逐渐达到峰值点，普遍在滑移量超过1 mm之后，随着滑移量的增加加载的荷载减小，荷载与位移呈现负相关关系。峰值荷载最大的为C50-L40×4-B150编号的试样，且其在试验末期的残余荷载值最大。

2.2 极限黏结强度的影响因素

假定黏结长度方向上的横截面在加载时的应力相同，那么可以通过平均黏结强度来作为标准，用以分析混凝土强度、黏结长度以及保护层厚度对角钢混凝土黏结界面的影响。平均黏结强度τ可通过式(1)得出[7]：

(1)

其中，P为试验时施加的荷载；la为黏结长度；Ca为角钢的横截面周长。

表4给出了各试样的黏结滑移特征值。从表4可以看出，Po/Pu为0.78～0.94之间，峰值滑移荷载对应的滑移量Su最大为0.63 mm。因此，应当重视角钢与混凝土之间的滑移，因为一旦角钢的初始滑移荷载出现，则很快就会演变成全截面滑移，在结构中形成较大的安全隐患。

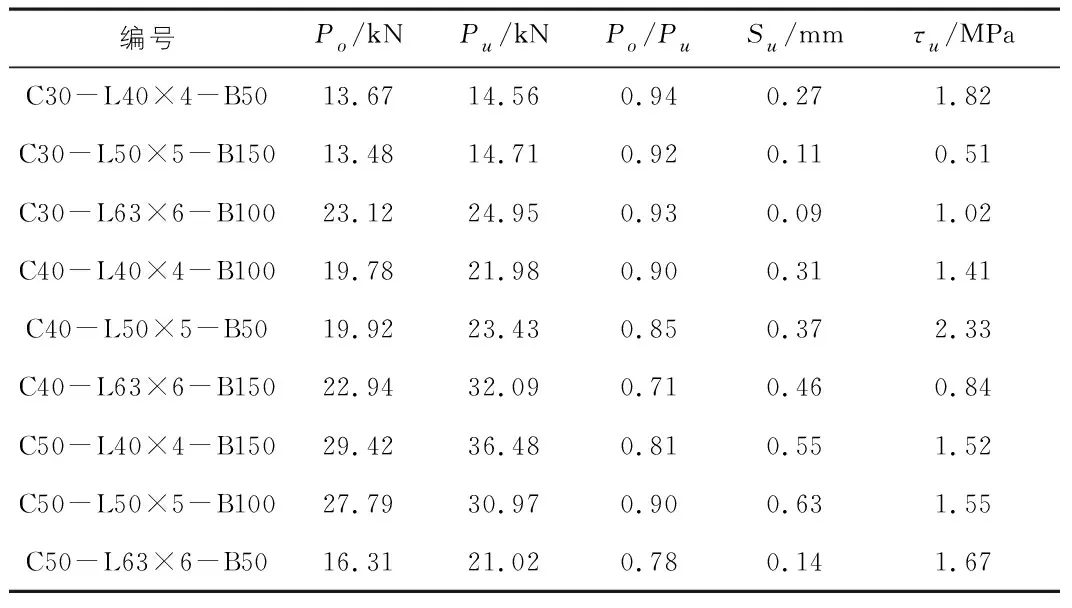
表4 黏结滑移特征值

基于极差分析法，分析了在正交试验中各因素对角钢-混凝土界面的极限黏结强度的影响。以前三种试样为例，图4展示了三种试样下的黏结强度、保护层厚度和混凝土强度的黏结强度效应。由黏结长度和极限黏结强度的相关性可以看出，黏结长度与极限黏结强度呈负相关关系，随着黏结长度的增大，极限黏结强度减小，且在50 mm～100 mm黏结长度范围内的极限黏结强度的减小速率大于在100 mm～150 mm黏结长度范围内的极限黏结强度的减小速率。

Path Planning of Unmanned Surface Vehicle Based on Variable Mesh Improved Genetic Algorithm

由保护层厚度与极限黏结强度的相关性可以看出，混凝土保护层厚度与极限黏结强度为正相关关系，随着混凝土保护层厚度的增加，极限黏结强度亦增大，且在30 mm～39 mm保护层厚度范围内的极限黏结强度的增大速率大于在39 mm～46 mm保护层范围内的极限黏结强度的增大速率。

由混凝土强度等级与极限黏结强度的相关性可以看出，混凝土强度等级与极限黏结强度为正相关关系，随着混凝土保护层厚度的增加，极限黏结强度显著提高。与保护层与极限黏结强度的关系类似，极限黏结强度的增大速率随混凝土极限抗压强度的增加而逐渐减小。这是由于增大混凝土极限抗压强度，会增大混凝土对角钢的环箍作用，使得角钢不易与混凝土产生相对滑移，因而使得极限黏结强度显著提高。

3 有限元计算

为了增加分析的可靠性，以及进一步对角钢-混凝土界面的黏结作用分析，本文利用有限元软件建立了角钢混凝土模型，并与试验结果进行对比以验证模型的有效性，并根据验证过的模型对角钢混凝土界面黏结效应的丧失过程进行动态模拟。

3.1 有限元模型建立

根据相关模拟研究，并结合实际工程经验，利用摩尔库仑柔性结构模型模拟混凝土，角钢通过软件内置的刚性板单元进行模拟。混凝土与角钢界面通过设置接触单元进行模拟。界面之间的摩擦效应参考库仑摩擦模型来进行实现，其中的摩擦系数μ初值设置为0.45。

为了在保证计算精度的前提下兼顾计算效率，在网格划分时对角钢与混凝土接触界面进行局部网格加密处理，其他部分网格划分为细，共划分出166 314个10节点有限元网格。上端边界条件设置为自由，其余方向边界条件均设为固定端。图5展示了有限元网格模型。

3.2 模拟结果与试验结果的比较

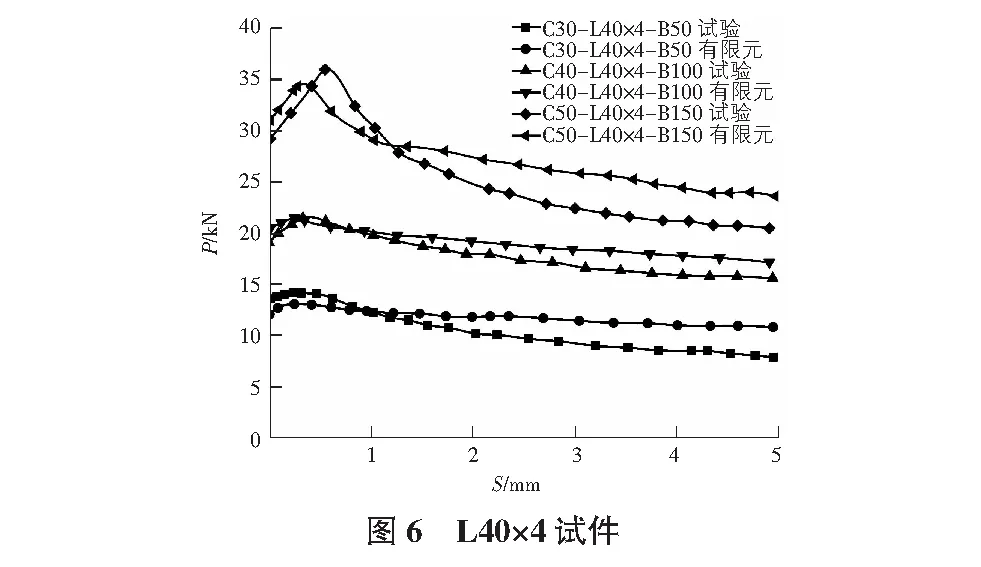
图6～图8分别展示了L40×4型号角钢、L50×5角钢和L63×6角钢的有限元模拟结果与试验结果对比情况。从图中可以看出，有限元数值模拟结果与试验结果较为吻合，趋势和数值均较为接近，说明有限元模型的建立具有一定的合理性。

此外，从图6可以看出，在试验的初期阶段，滑移量比较小时，数值模拟结果小于试验结果，而峰值点过后，数值模拟结果均大于试验结果，这是由于数值模型的材料破坏过程为线性，以及摩擦力变化形式在前期为线性递增，在试验中后期一直保持一个定值，并且未能考虑实际材料的不均匀性和各向异性，而是采用了均匀性和各向同性假设，与实际情况仍然存在些差异，因此在破坏阶段与试验结果存在一定的出入。这种情况在图8中表现得更为明显。这也说明，虽然数值模拟是一种高效的工具，可以降低计算难度和计算量，但不能仅以此作为工程评判问题的唯一依据。

3.3 黏结机理分析

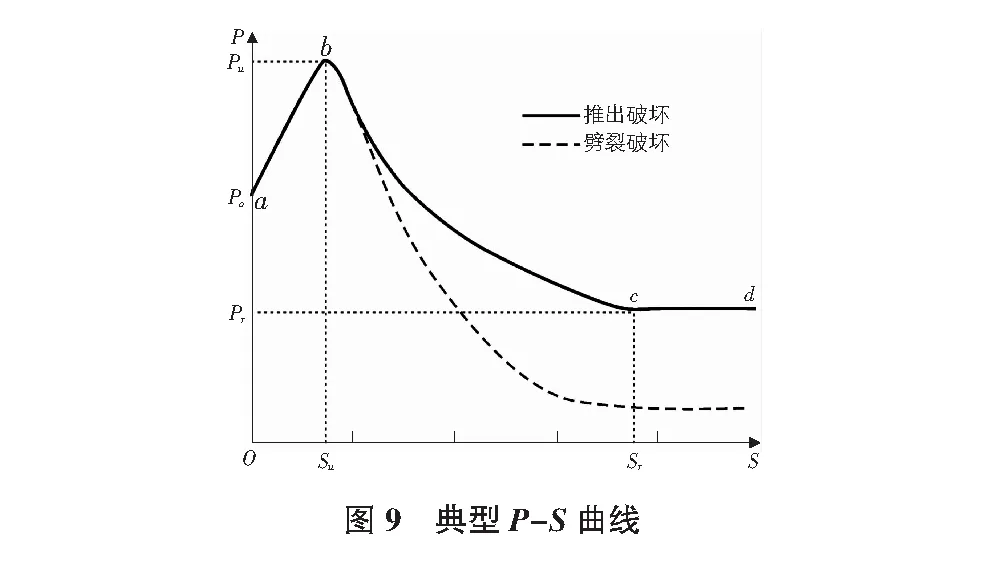
根据以上通过试验方法和有限元方法对黏结强度与滑移量关系的研究，对角钢混凝土的破坏形式做了总结。角钢混凝土的破坏形式可归纳为推出破坏形式和劈裂破坏形式。图9展示了加载端荷载与滑移量的关系曲线。从图9中可以看出，加载端荷载-滑移曲线若发生推出破坏可分为四个阶段：第一阶段为Oa胶结段，第二阶段为ab上升阶段，第三阶段为bc下降阶段，最后为cd残余阶段。而劈裂破坏是在试验过程中，混凝土发生开裂而导致的脆性破坏，因此仅存在胶结阶段和上升阶段，到达峰值之后黏结强度迅速下降，试件发生破坏。

4 结论

本文采用正交试验，对影响角钢-混凝土界面黏结强度的因素进行了分析，通过极差分析法，确定了各因素对黏结强度的影响效果。基于此，利用有限元软件建立了角钢-混凝土三维模型，并利用本文试验结果验证了模型的有效性，对比了与试验结果的差异，推导出了角钢混凝土破坏的两种形式以及对应阶段，得出主要结论如下：

1)黏结长度与极限黏结强度呈负相关关系，随着黏结长度的增大，极限黏结强度减小，且在50 mm～100 mm黏结长度范围内的极限黏结强度的减小速率大于在100 mm～150 mm黏结长度范围内的极限黏结强度的减小速率。

2)混凝土保护层厚度以及混凝土强度均与极限黏结强度为正相关关系，随着混凝土保护层厚度和混凝土强度的增加，极限黏结强度亦增大，且增大速率逐渐减缓。

3)有限元数值模拟结果与试验结果较为吻合，趋势和数值均较为接近。在破坏阶段，有限元模拟结果与试验结果相比略大，这是由于数值模拟采用了材料均匀性和各向异性的假设，使得模拟结果与试验结果存在差异。

4)角钢混凝土的破坏形式可归纳为推出破坏形式和劈裂破坏形式。若发生推出破坏可分为四个阶段，分别为胶结阶段、上升阶段、下降阶段和残余阶段。而劈裂破坏仅存在胶结阶段和上升阶段。