船舶机械与船体耦合结构振动输入阻抗的计算与分析

蔡连捷，杨平

（扬帆集团股份有限公司，浙江 舟山 316100）

船体噪声的主要来源是船舶机械的工作噪声，船舶安全、平稳的运行受到严重影响，是船舶噪声控制领域的重要研究方向。机械设备的振动将通过基座向船体结构传递，船舶系统隔振性能的好坏受到该耦合结构阻抗特性以及它与隔振系统的匹配情况的影响。

船体结构的阻抗特性是机械设备振动能量的阻绝能力的重要标志，机械设备传递给船体的阻抗值与振动能量成反比，随着阻抗值的增大，船体结构振动产生的声辐射将减小，因此，机械阻抗值的大小是判断船体隔振能力的一个重要依据，本文采用理论计算法与有限元分析法相结合的分析方法，进行了“机械设备-船体”耦合结构的输入阻抗的计算与分析，机械阻抗作为船舶隔振系统分段振动特性的表征量，对于预报船舶机械噪声构成具有重要的意义。

1 输入阻抗的理论计算

1.1 计算方法

船舶的结构是组合结构，由若干个分段单元组成，在激励力作用下，如果各单元的振动速度相同，则认为各个单元的输入阻抗并联组成船舶结构的总输入阻抗，由公式（1）可以计算获得；反之，船舶结构总的输入阻抗是由各个单元输入阻抗串联而成，具体计算方法是，先由公式（2）计算船舶结构的导纳，再求解导纳的倒数值，最后船舶结构总的输入阻抗计算获得。

由式（3）可知，船舶各个分单元的输入阻抗最大值可以被认为是总并联结构的输入阻抗值，式（4）而知，各个分单元的输入阻抗最小值决定了串联组合结构的总输入阻抗值。

设备基座与船体结构是复杂的空间结构振动系统，因为它是有限尺度的结构，它的边界条件确定难度较大，因此，1Hz～10kHz的输入阻抗值很难精确地被计算出来，由于不同频率的结构的动力特性是不相同的，需建立不同动力特性相应的振动模型。

1Hz～10kHz频率范围，船体振动由全船振动、舱段振动、板格振动三部分组成，依据等截面Timoshenko梁自由振动方程来求解，见式（5）。

式中，E为振动梁的弹性模量；G为振动梁的剪切弹性模量；r为振动梁的密度；I为振动梁中性轴的惯性矩；A为振动梁的横截面积；w为振动梁横向的位移；K*为弹性基础的支撑刚度系数，к为Timoshenko剪切的修正系数；φ为振动梁转角；t为时间变量；x为一维空间的坐标变量。

在低频段的振动，船体结构属于细长类结构，此时，振动模态主要的表现形式为整船刚性的梁式弯曲，船舶主体结构的弹性波波长远远大于各舱段的长度值，梁的横截面没有发生变形，因此，梁“平截面”的假设是成立的。阻尼损耗被考虑，最小输入机械阻抗可近似得到如式（6）。

式中，ms为单位长度船体梁的质量；mw为单位长度附连水的质量；CB为梁弯曲的波速；k为梁弯曲振动的波数；l为梁的长度；η为阻尼损耗的因子。

在中频率振动段，振动的波长将减小，当弯曲波半波长的1/2小于单个舱段长度时，单个舱段开始出现周向的振动模态，不同于梁式振动模式，周向振动将在模态叠加过程中起主要作用，此时，由于相邻舱段的影响很小，可以忽略不计，两端舱段结构的简支式的力学模型可以被简化。

此时，总输入阻抗为总输入导纳的倒数，如式（7）。

在中高频率振动段，当设备基座腹板与肋板的间距大于弯曲波的半波长时，局部振动开始出现在设备基座的板架结构，在船舶的各个舱段部分，船体结构离设备基座越远，它对设备基座振动的响应将越小，此时，基座自身结构和附近的船体支承形式决定了设备基座的阻抗特性。

1.2 计算结果及分析

根据上述计算方法，耦合结构的输入阻抗随频率变化规律，见图1。计算结果显示，设备基座与船体耦合结构的输入阻抗将随着频率增加而减小，在低频段振动部分，耦合结构的输入阻抗变化较剧烈，在高频振动段，结构的输入阻抗变化不大，并逐渐逼近88463.81（Ns/m）这一固定的值。

图1 耦合结构的输入阻抗理论计算值

2 输入阻抗的有限元分析

2.1 建模

水面舰船的尺寸是分频时的主要依据，在10～20Hz振动频率范围内，采用的是全船模型；在20～200Hz振动频率范围内，采用的是舱段模型；在200Hz～10KHz振动频率范围内，采用的是肋段模型。

为保证计算结果正确，有限元法要求，在模型中的一个波长内至少包含5个节点，因此，可以根据式（9）确定模型网格尺寸，所建的模型如图2。

图2 耦合结构的有限元模型

2.2 计算结果及分析

采用有限元法进行分析时，振动频率频段选取为1Hz～10kHz，其中，在1～100Hz振动频段内，计算方法采用扫频方式，在100Hz～10kHz振动频段内，计算方法采用1/3倍频程的中心频点（图3）。

图3 有限元法的计算模型

通过有限元分析可得ZF1，得到的分析结果如图4。由分析的结果可知，在1～20Hz低频率振动段，船舶振动的主要特征是全船振动，在这个频段，耦合结构输入阻抗的曲线出现明显变化；在20～100Hz中频段，内舱段结构开始出现振动，输入阻抗的曲线斜率变化变快；在100～1000Hz高频振动段，耦合结构输入阻抗的变化开始较小，且呈现逐渐平稳趋势，该频段输入阻抗值是由基座面板的参数决定的。

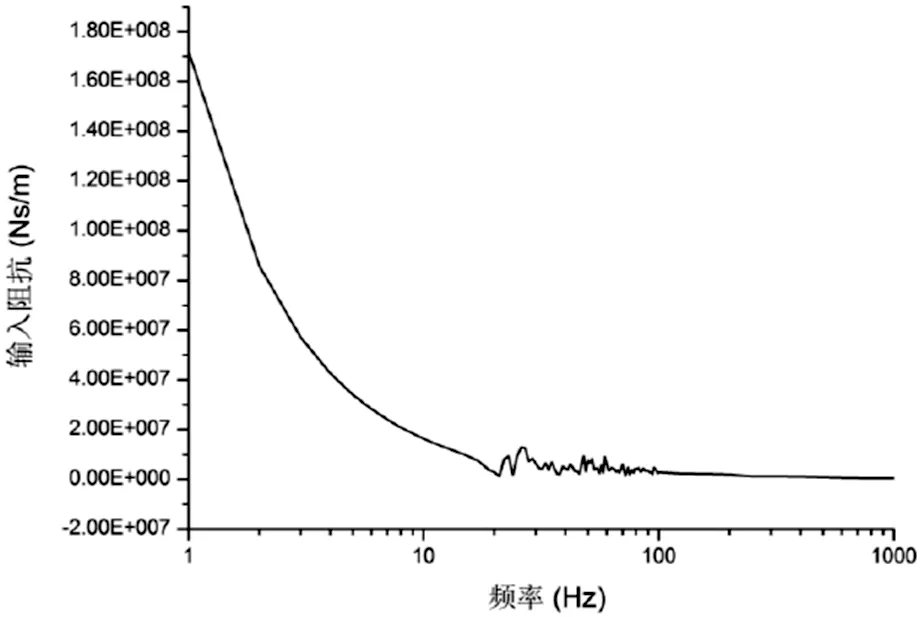
图4 采用有限元法的计算结果

3 结语

3.1 两种分析方法的结果（图5）

图5 耦合结构输入阻抗两种方法计算结果对比

3.2 结论

采用理论计算法和有限元分析法，两者的计算结果相近。在1～20Hz的低频率段内，两种方法所得到的结果变化规律基本一致，且误差不大；在20～100Hz频率段内，两种方法的分析结果具有较大的差异，采用理论计算法获得的阻抗曲线比较平滑，采用有限元分析法获得的阻抗曲线变化较明显，建立这个频段的模型相对较复杂，主要是因为某些强度不高的结构振动造成了计算结果的差异性，而在使用理论计算法时，该频段的模型被简化和等效，强度较小的结构振动被忽略，引起了这种差异性；在100Hz～10kHz频段内，两种计算方法获得的结果保持一致。