瑞利数对竖直恒温面处自然对流边界层不稳定性的影响
2022-05-25王春雨刘泽勤刘聪聪赵鹏鹏
王春雨,刘泽勤,刘聪聪,赵鹏鹏
(1.天津商业大学 机械工程学院,天津 300134; 2.天津商业大学 冷冻冷藏技术教育部工程研究中心,天津 300134; 3.天津商业大学 天津市制冷技术重点实验室,天津 300134; 4.扬州大学 水利与能源动力工程学院,江苏 扬州 225009)
0 引 言
边界层不稳定性特征是自然对流研究领域中的重要课题,认识边界层不稳定性,有助于理解层流至湍流的转化、强化对流换热等问题。早在20世纪50年代,有关边界层不稳定性的研究已经展开。文献[1]最早通过马赫-曾德尔干涉仪(Mach-Zehnder interferometer)观察受到扰动的层流边界层,并发现热边界层能够放大该扰动,并最终过渡至湍流流动,该现象即为边界层的不稳定性;文献[2-3]研究了使用丝带在竖直面附近产生震动,进而观察扰动对边界层的影响,实验结果表明,竖直边界层仅能放大特定频率内的扰动。当边界层同时受到低频和高频扰动时,边界层的不稳定性取决于高频扰动[4-5],而非低频扰动。模拟中常用随机变化的热流区域或温度边界使边界层产生不稳定性,文献[6]探究在竖直恒温面的上游位置引入随机式变化的热流下,观测自然对流边界层内部温度时间序列的功率谱。模拟结果表明在边界层上游区,低频带的功率值远高于高频带,即低频扰动占主导作用,随着边界层向下游发展,低频带不断衰减,高频带对应功率值升高。根据功率谱的频带分布,自然对流竖直边界层可划分为上游低频区、过渡区(既有高频带也有低频带)以及下游高频区[7-8]。利用边界层不稳定性特征能够实现共振强化对流换热,文献[9]研究在竖直边界层上游引入正弦式变化的热流区域,其变化频率与边界层的特征频率相同,从而实现共振强化换热。结果发现,相比于无扰动状态下的对流换热,在频率为特征频率的正弦扰动下,对流换热量提高了44%。
目前,关于竖直恒温面处边界层不稳定性的研究相对较少,有关瑞利数Ra对边界层不稳定性影响的研究还需进一步进行。因此本文对不同Ra下,普朗特数Pr=6.24的竖直恒温面处的自然对流进行模拟,探究Ra对自然对流边界层不稳定性的影响。
1 数学与物理模型
1.1 物理模型
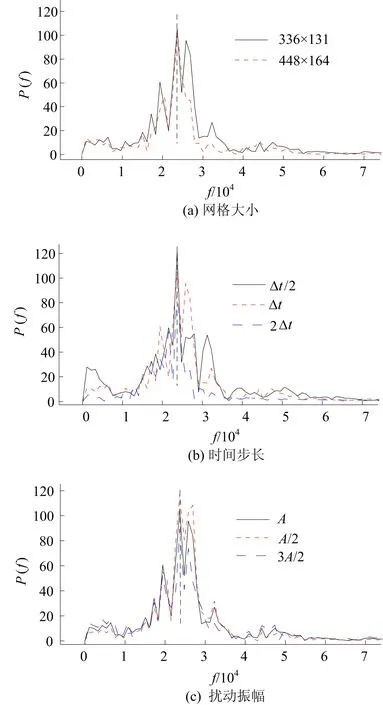
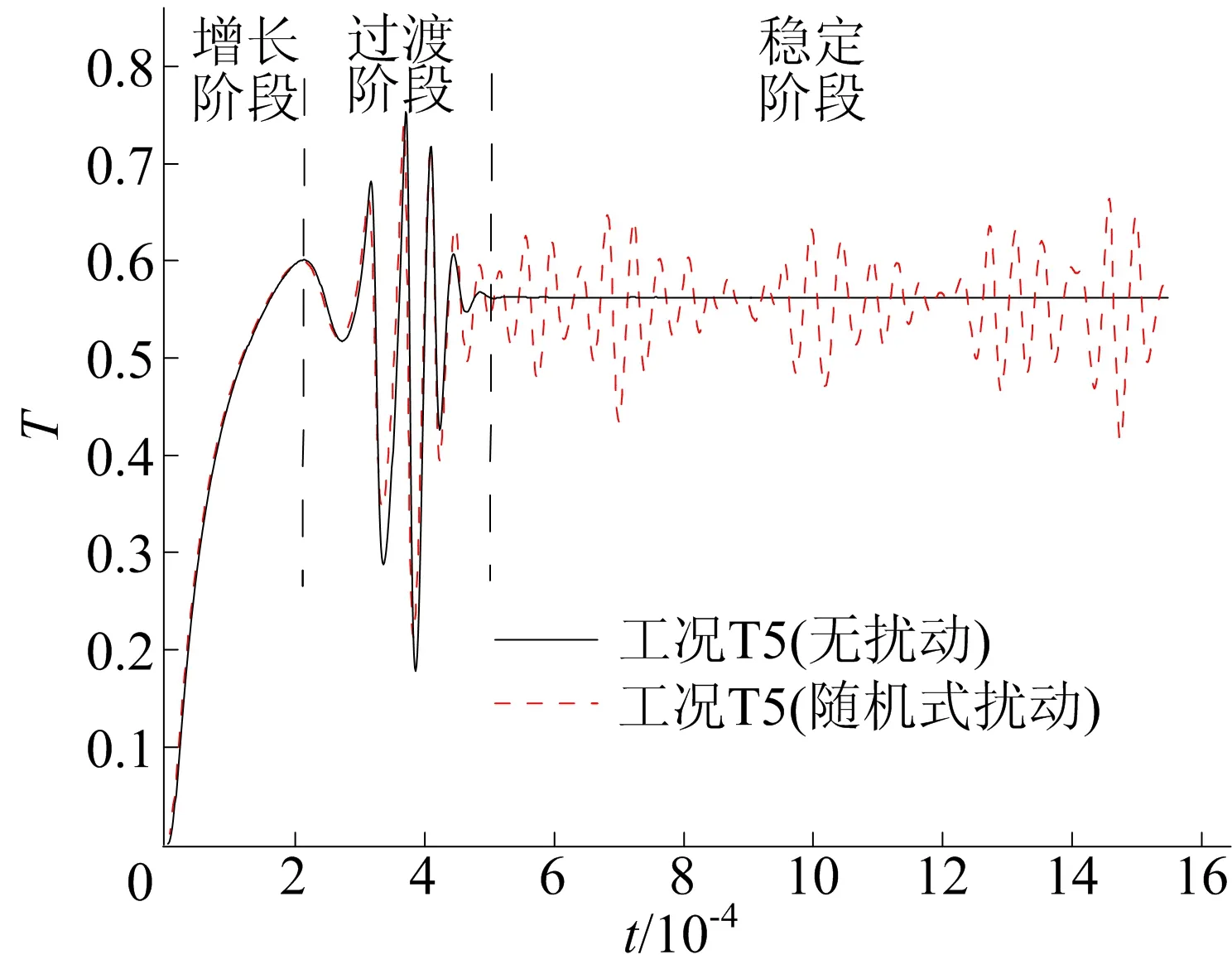
模拟所选二维模型如图1所示,左边界OF为恒温面,其高度为0.24 m,记为H。为避免水平边界对竖直边界层产生影响[10],分别向竖直恒温面上、下方向延长0.2H。考虑到黏性边界层的厚度影响[11],模型的宽度设置为0.5H。扰动区域设置在OE处,其范围为0 图1 模拟模型 表1 边界条件 假设流体为不可压缩流体,且采用Boussinesq假设,自然对流的二维无量纲控制方程组为: (1) (2) (3) (4) 其中:U=u/(γH-1);V=v/(γH-1);X=x/H;Y=y/H;t=τ/(H2γ-1);P=p/(ργ2H-2);T=(φ-φ0)/(φw-φ0);U、V、X、Y、t、P、T分别为u、v、x、y、τ、p、φ的无量纲形式;u、v分别为x、y方向的速度;p为压力;τ为时间;ρ为密度;φ为温度;γ为流体动力黏性系数;φ0为初始流体温度;φw为垂直恒温面温度。 规定频率为F,无量纲频率为f,频率按照f=FH2γ-1进行无量纲化,本文所述频率均为无量纲频率。 自然对流的状态取决于无量纲瑞利数Ra和普朗特数Pr,计算公式为: (5) Pr=γ/κ (6) 其中:g为重力加速度;β为热膨胀系数;κ为热扩散系数;γ为流体动力黏性系数;Δφ=φw-φ0。 扰动区设置在范围为0 模拟中,不同工况下流体的初始温度均为298.15 K,该状态下γ的值为0.892 92×10-6m2/s,β的值为0.000 25,κ的值为0.143×10-6m2/s,通过(6)式可以算得Pr为6.24。Ra的值与恒温面和流体间的温差、恒温面的高度有关,由于恒温面的无量纲高度恒定为1(量纲长度为0.24 m),因此Ra取决于恒温面和初始流体间的温差,即模拟通过改变恒温面的温度,达到改变Ra的目的。模拟工况所选用的Ra分别为5.31×108、7.97×108、1.06×109、1.33×109、2.66×109、3.98×109、5.31×109,上述Ra对应的壁面温度分别为300、301、302、303、308、313、318 K,对应的恒温面与初始流体间的温差分别为2、3、4、5、10、15、20 K。模拟工况见表2所列。 表2 模拟工况 分别对网格、时间步长和扰动振幅进行独立性检测,独立性检测工况见表3所列。选用不同网格数量、时间步长和扰动振幅进行模拟,记录不同工况下相同测点(X=0.004 2,Y=0.830 0)处的温度时间序列,再将测点的温度时间序列导入MATLAB中进行快速傅里叶变换,将时域内的温度信号处理至频域的频率信号,通过MATLAB导出温度时间序列的功率谱,功率谱显示了不同频率所对应的功率值,其中对应功率值最大的频率即为峰值频率。对比不同工况下的峰值频率和功率谱分布趋势,完成独立性检测。 表3 独立性检测工况 首先对网格大小为336×131、448×164的2种网格(工况a、工况b)进行模拟,模拟选用时间步长为Δt,其值为1.3×10-6,扰动振幅为A,其值为1,独立性检测如图2所示。 图2 独立性检测 测点(X=0.004 2,Y=0.830 0)处温度时间序列的功率谱如图2a所示。功率谱的横坐标f为温度变化的频率,纵坐标P(f)为每个频率所对应的功率值。 由图2a可知,在2种不同网格大小下,功率图分布趋势大致相同,且对应功率值最大的无量纲频率相同,均为23 676(对应的非无量纲频率为0.33 Hz),规定该频率为峰值频率fc。为保证计算的精确度,且避免计算量过大,下面选用网格大小为336×131的模型。 选用网格大小为336×131的模型,分别使用Δt、Δt/2、2Δt的时间步长(工况a、工况c、工况d)进行模拟,扰动振幅为A,测点(X=0.004 2,Y=0.830 0)处温度时间序列的功率谱如图2b所示。 由图2b可知,在3种不同的时间步长下,功率谱的分布规律相似,且峰值频率fc相同,均为23 676。为保证计算的精确度,选用Δt的时间步长。 选用网格大小为336×131的模型,分别使用振幅为A、A/2、3A/2扰动(工况a、工况e、工况f)进行模拟,时间步长为Δt,得到测点7的温度功率谱如图2c所示。 由图2c可知,在不同扰动振幅下,功率谱的分布规律相似,且得到的峰值频率fc相同,均为23 676。为保证计算准确度,选择振幅为A的扰动。 综上所述,本文选用网格大小为336×131、时间步长为1.3×10-6、振幅为1的模型进行模拟。 在ANSYS FLUENT定义运行文件,模拟为非稳态模拟,选用压力-速度耦合以及层流模型。流体采用Boussinesq假设,应用有限体积法和SIMPLE算法求解控制方程,不稳定项采用二阶向后差分格式进行积分,空间导数采用二阶中心差分格式进行离散。 根据独立性检测选用网格大小为336×131的模型,时间步长选用0.083 25 s,其对应的无量纲时间步长为1.3×10-6。为记录模拟开始后100 s内的自然对流边界层的变化情况,时间步长的步数为1 200,每一时间步长的最大迭代次数为20次,收敛方案中最大残差值设为10-4,按上述内容设置好后进行求解工作。 对表2中T1~T7工况,即不同瑞利数Ra下,竖直恒温面处的自然对流进行模拟。以T1、T5、T7工况为例, 3种工况下竖直恒温面处的自然对流热边界层如图3所示。 图3 T1、T5、T7工况下的竖直热边界层 图3中Y轴代表竖直恒温面,即模型中的OF边。由图3可知,热边界层内温度分层均匀,边界层流动处于层流状态,且在3种不同工况下,T1工况下热边界层厚度最大,T7工况下热边界层厚度最小。该现象证明,随着Ra增大,边界层厚度减小,边界层内温度梯度增大。 为探究自然对流边界层的不稳定性,确定热边界层的特征频率,在扰动区加入随机式扰动,使扰动区的温度呈2A(Rand(0,1)-0.5)的数学形式变化。对工况R1~工况R7,即随机式扰动下,不同Ra下的自然对流进行模拟。以R1、R5、R7工况为例, 3种工况下竖直恒温面处的自然对流热边界层如图4所示。由图4a可知,在R1工况下,热边界层出现明显的波动,非线性增强,且随着热边界层由上游发展至下游,其波动程度增强。由图4可知,R1工况下热边界层的厚度最大,R7工况下热边界层厚度最小,该现象证明随着Ra增加,随机式扰动下的边界层厚度逐渐减小,该现象与无扰动状态下的边界层规律相同。 图4 R1、R5、R7工况下的竖直热边界层 以工况T5 、工况R5为例,记录并对比2个工况下测点(0.004 2,0.830 0)处的温度时间序列,结果如图5所示。将无扰动与随机式扰动状态下测点处的温度时间序列划分为增长阶段、过渡阶段和稳定阶段[10](图5),在增长阶段和过渡阶段,测点的温度变化趋势相同,温度值相差不大,在稳定阶段存在明显差异。无扰动状态下,测点的温度稳定维持在定值处,随机式扰动下,测点的温度则呈现出不规则波动。该现象证明,边界层上游的随机式扰动对边界层在增长阶段和过渡阶段的影响不大,其影响主要体现于稳定阶段。 以R5工况为例,选取测点1(0.004 2,0.042 0)、测点2(0.004 2,0.170 0)、测点3(0.004 2,0.500 0)、测点4(0.004 2,0.830 0),并记录在随机式扰动下测点处的温度时间序列,结果如图6所示。通过对比4个测点处的温度时间序列,发现随着Y坐标的增大,即随着边界层高度的增加,测点在稳定阶段内的温度波动增加,该现象证明竖直自然对流边界层能够放大上游位置的扰动。其中,测点4在稳定阶段的温度波动最大,测点1在稳定阶段的温度波动最小。 为确定热边界层的特征频率,将上述4个测点在稳定阶段的温度时间序列(5×10-4 图5 T5 、R5工况下测点(0.004 2,0.830 0)处温度时间序列 图6 R5工况下测点1~测点4处温度时间序列 图7中,频率均为无量纲频率,纵坐标P(f)为功率值。观察测点1(0.004 2,0.042 0)处温度时间序列的功率谱,如图7a所示。在热边界层内测点1处,频率范围0~20 000对应的功率值较大,且峰值频率为10 762,该现象说明在边界层上游,低频带占主导作用。观察测点2(0.004 2,0.170 0)处温度的功率谱,如图7b所示。相对测点1而言,在热边界层内测点2的位置,频率范围为0~10 000对应功率值下降,频率范围为20 000~30 000对应的功率值上升,且峰值频率为23 676,该现象说明随着边界层高度的升高,占主导作用的频率带向高频区移动。观察测点3(0.004 2,0.500 0)、测点4(0.004 2,0.830 0)处温度的功率谱,如图7c、图7d所示,频率范围为15 000~30 000对应的功率值较大,峰值频率均为23 676,该现象说明在边界层的中下游,高频带占主导作用。上述现象证明竖直边界层的发展可分为上游低频区、过渡区、下游高频区3个阶段。由于热边界层的不稳定性取决于高频扰动[12],规定下游边界层的高频峰值频率为特征频率,即工况R5下的自然对流边界层的特征频率为23 676。 图7 R5工况下测点1~测点4处温度时间序列功率谱 为确定不同Ra的自然对流热边界层的特征频率,对工况R1~工况R7,即对随机式扰动下,不同Ra状态下的自然对流进行模拟,导出不同工况下测点4的温度时间序列,并对其进行快速傅里叶变换,得到不同Ra下自然对流边界层的特征频率,进而得到特征频率与Ra之间的拟合关系式,结果如图8所示。Ra为5.31×108、7.97×108、1.06×109、1.33×109、2.66×109、3.98×109、5.31×109状态下的竖直自然对流边界层所对应的无量纲特征频率分别为6 457、12 914、15 066、16 143、23 676、32 286、38 743,由此可知,在Ra为5.31×108~5.31×109的范围内,随着Ra增加,自然对流边界层的特征频率增加。 图8 特征频率fc与Ra的拟合关系式 应用Origin软件,对特征频率fc与Ra的值进行拟合,得到特征频率fc与Ra之间的关系式,即fc=0.226Ra0.641。 为了解频率为特征频率的正弦式扰动对热边界层不稳定性的影响,在扰动区设置频率为特征频率的正弦式扰动,使扰动区的温度呈T=Asin(2πfct)的数学形式变化。对工况S1~工况S7进行模拟,并导出各工况下自然对流热边界层图。以S1、S5、S7工况为例,3种工况下竖直恒温面处的自然对流热边界层如图9所示。 由图9a可知,工况S1下的热边界层产生剧烈波动,且随着热边界层由上游发展至下游,波动程度增强。对比图4、图9可知,相比于随机式扰动,正弦式扰动下热边界层的波动程度更大。由图9可知,随着Ra增加,热边界层的整体厚度减小,整体温度梯度增加,该现象与无扰动状态下的温度梯度边界层梯度规律相同。 图9 S1、S5、S7工况下的竖直热边界层 通过对竖直恒温面处的自然对流现象进行模拟,探究不同Ra状态下的自然对流边界层的不稳定性。模拟首先验证了竖直恒温面处自然对流边界层的不稳定性,以及热边界层可分为上游低频区、过渡区、下游高频区3个区域。另外,模拟结果表明在无扰动、随机式扰动和正弦式扰动状态下,随着Ra增大,竖直恒温壁面处的自然对流热边界层整体厚度均减小;在随机式扰动和正弦式扰动下,竖直恒温面处的自然对流热边界层沿竖直方向存在振荡,且相比随机式扰动,正弦式扰动下的热边界层的震荡幅度更大;Ra为5.31×108、7.97×108、1.06×109、1.33×109、2.66×109、3.98×109、5.31×109状态下的竖直自然对流边界层所对应的无量纲特征频率分别为6 457、12 914、15 066、16 143、23 676、32 286、38 743,Ra在5.31×108~5.31×109的范围内,自然对流边界层的特征频率与Ra间的耦合公式为fc=0.226Ra0.641。

1.2 数学模型
1.3 扰动设置
1.4 模拟工况

1.5 网格独立性检测

1.6 计算求解
2 模拟结果及分析
2.1 竖直恒温面处自然对流边界层的温度特性

2.2 随机扰动下的自然对流边界层不稳定性




2.3 正弦扰动下自然对流边界层不稳定性

3 结 论
