考虑流固耦合的空调管路动力学响应分析
2022-05-25卢剑伟任远凯
杨 凡,卢剑伟,任远凯
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
配管是空调器的重要部件,也是空调外机中最薄弱、最容易损坏的结构件之一,一直以来都是空调外机产品开发过程中的一个难点。配管振动的起因主要有2种:① 压缩机转子不平衡引起的自身振动;② 压缩机吸排气产生的制冷剂压力脉动产生的激励。空调器工作时,这2种情况会同时发生,且制冷剂压力脉动产生的激励会与压缩机振动引发的配管振动耦合在一起,因此,考察配管振动需要考虑流固耦合的影响。
为了考察配管系统的疲劳可靠性等问题,通常采用虚拟样机技术对压缩机配管系统进行动力学建模,并以压缩机载荷作为激励对配管系统的振动及应力等动力学响应进行评估。本课题组在前期工作中已经提出了稳态及瞬态工况下压缩机载荷激励的识别方法[1-3],掌握了压缩机激励下的配管动力学分析方法[4]。由于管内制冷剂的压力状况较难通过实验获取,本文尝试建立配管流固耦合分析模型,并通过传递矩阵法求解得到稳定工况下管内流体的压力分布。在此基础上,考虑流体载荷激励的影响,以某款空调配管系统为例进行流固耦合作用下配管动力学响应分析,为压缩机配管系统的振动分析与可靠性设计提供依据。
1 配管系统流固耦合动力学建模
1.1 典型管路元件流固耦合模型的建立
管路流固耦合形式主要包括泊松耦合、摩擦耦合和Bourdon耦合[5-6]。泊松耦合反映流体和固体变形之间的相互作用,是管路流固耦合分析的主要耦合形式;摩擦耦合是黏性流体与管壁之间的摩擦而形成的边界接触耦合;Bourdon耦合是由于弯管截面形状发生变化所产生的耦合效应。
流体管道示意图如图1所示,与水平成β角。
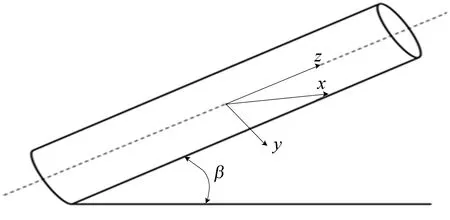
图1 直管示意图
方程的推导以Timoshenko梁模型为基础,由于黏性摩擦力对系统动力特性的影响很小,忽略摩擦耦合效应,考虑泊松耦合以及流体压力、重力等因素,动力学方程[7]描述如下。
(1) 轴向动力学模型。模型如下:
(1)
(2)
(3)
(4)
(2) 横向振动模型(y-z平面)。模型如下:
(5)
(6)
(7)
(8)
(3) 横向振动模型(x-z平面)。模型如下:
(9)
(10)
(11)
(12)
(4) 直管扭转振动模型。模型如下:
(13)
(14)

M=ρpAp+ρfAf,B=ρpIp+ρfIf,
弯管模型是由直管模型扩展而来,增加了由弯曲导致的不平衡项1/Rw,当Rw趋向于无穷大时,弯管的动力学方程与直管的方程相同。
1.2 传递矩阵法求解
上述方程组中共包含14个变量,可用状态向量y(z,t)表示如下:

因此,受到外部激励r(z,t)作用的直管流固耦合模型可写成如下矩阵形式:

(15)
对上述方程进行Laplace变换,令
Φ(z,s)=L(y(z,t)),R(z,s)=L(r(z,t)),
(16)
其中

H(z,s)=R(z,s)-Ay(z,t)|t=0-D/s。

(17)


(18)
进而有:
(19)
因此方程(19)的形式解为:
v(z,s)=E(z,s)v0(z,s)+q(z,s)
(20)
其中,v0(z,s)为未知的列向量,其值取决于边界条件,其余向量大小如下:
v(z,s)=[v1(z,s)v2(z,s)…v14(z,s)]T,
T=diag{λ1(s),λ2(s),…,λ14(s)},
q(z,s)=[q1(z,s)q2(z,s)…q14(z,s)]T,
将v(z,s)=V-1Φ(z,s),v0(s)=V-1Φ(0,s)代入方程(20),整理可得:
Φ(z,s)=MΦ(0,s)+Q(z,s)
(21)
其中:M=VE(z,s)V-1为管路传递矩阵;Q(z,s)=Vq(z,s)为外部激励和重力共同作用组成的状态向量。弯管的求解方法类似。
1.3 空调配管传递矩阵
压缩机配管系统通常由多段直管与弯管组成,因此需要计算每段管路的传递矩阵,建立整体的传递矩阵。假设空调管路含有n段直管和弯管,则整个首尾管路状态向量的传递关系可以表示为:
Φn=MnΦn-1+Qn(ln,s)=
Mn[Mn-1Φn-2+Qn-1(ln-1,s)]+Qn(ln,s)=
MnMn-1Mn-2Φn-3+MnMn-1Qn-2(ln-2,s)+
MnQn-1(ln-1,s)+Qn(ln,s)=…=
MnMn-1…M1Φ0+MnMn-1…M2Q1(l1,s)+
…+MnQn-1(ln-1,s)+Qn(ln,s),
整理可得:
Φn=M(n)Φ0+N(n-1)
(22)
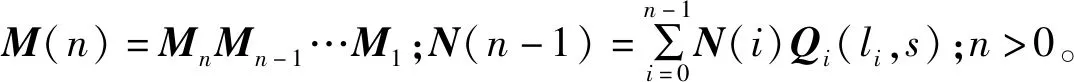
在求解配管系统中,当管路的轴线异面时,计算时需要进行坐标变换,坐标变换关系为:
Φm=SmΦm-1
(23)
Sm为坐标变换矩阵,其表达式为:
(24)
其中,β为坐标旋转角度。Φstart和Φend分别满足一个边界方程,即
DstartΦstart=Fstart,DendΦend=Fend。
对于空调配管系统,管路皆与质量较大的部件连接,故假设管路固支,在边界处流体压力及管路结构的各向振速均为0,则对应的矩阵形式[8]如下:
D=

(25)
联立方程得到总体的传递矩阵形式为:
DtotΦtot=F
(26)
其中
2 空调管路流固耦合动力学响应分析
2.1 有预应力的模态分析
为了进行配管系统的流固耦合动力学响应分析,首先要对管路进行模态分析,提取配管系统的模态参数。
本文以某型号压缩机配管系统为研究对象,其材料参数见表1所列。基于ANSYS软件按照表1参数建立该机型的有限元模型,如图2所示。其中,压缩机减振橡胶底角与压缩机钢制底角之间直接定义节点-节点自由度耦合约束,管路系统中的所有焊接采用刚性连接,配管与冷凝器、底盘连接处采用固定约束。
配管系统主要承受压缩机低频激励,因此配管结构低阶的模态是主要关注对象。由于配管管内制冷剂压力对配管结构会产生一定的预应力,因此,建模分析过程中考虑了制冷剂平均压力对配管系统模态的影响。有无预应力空调配管模态分析结果的对比见表2所列。

表1 材料参数

图2 压缩机配管系统有限元模型

表2 空调配管模态分析结果 单位:Hz
从表2可以看出,对于同一配管系统,在添加预应力后,其结构的各阶固有频率会相对增大。因此,在进行仿真分析时考虑预应力的影响是有必要的,这也与实际管路情况吻合。
2.2 空调配管谐响应分析
2.2.1 不考虑流固耦合的谐响应分析
通过对转子压缩机的结构分析可知,转子压缩机的主要激励为绕竖直方向的扭矩和径向力[9]。通过载荷激励反求出稳态工况下的压缩机载荷,基于建立的虚拟样机,以压缩机载荷作为激励进行谐响应分析,得到谐响应分析结果见表3所列。整机和各部件的位移云图如图3所示。

表3 不考虑流固耦合的配管谐响应分析结果

图3 不考虑流固耦合的压缩机配管系统位移云图
由表2和图3可知,当只有压缩机载荷时,配管系统中回气管振动较大,其余管路振动较小,低压阀接管、冷凝器接管最大应力值较小。
2.2.2 考虑流固耦合的谐响应分析
因为压缩机间歇性的吸排气,导致压缩机以脉冲形式吸排出高压气体,所以可假设排气管入口与回气管出口流体压力符合正弦函数,表达式如下:
P=P0+0.05P0sin(ωt)
(27)
其中:P为管内流体的平均压力;ω为转子压缩机工作频率。脉动压力的幅值一般为平均压力的5%。其余管路不与压缩机相连,流速和压力较为平缓,故假设管内压力均为平均压力。
根据(22)式建立排、回气管的整体传递矩阵,设置管路的边界条件,对排气管入口施加幅值为0.03 MPa的简谐激励,回气管出口施加幅值为0.01 MPa的简谐激励,得到与压缩机工作频率一致的流体压力值。将管内流体脉动压力和压缩机载荷同时作为激励对配管进行谐响应分析,得到的分析结果见表4所列。
整机和各部件的位移云图如图4所示。

表4 考虑流固耦合的配管谐响应分析结果
由表4和图4可知,考虑流体影响后,配管振动响应的最大位移点发生改变,排气管振动增大,回气管振动减小,并且整机及各部件的最大应力均有所增加。
由上述分析可知,流固耦合作用对配管动力学分析结果有较大影响,因此在进行配管的动力学分析时,有必要考虑冷媒脉动压力的作用。

图4 考虑流固耦合的压缩机配管系统位移云图
3 结 论
(1) 在稳态工况下,管路与流体压力之间的耦合作用对压缩机配管系统动力学响应具有较大的影响。考虑流固耦合后,排气管的振动与最大应力有较为明显的增大,且管路的位移分布发生较大变化。本文提出的考虑流固耦合的压缩机配管系统动力学响应分析方法为提高动力学响应分析的准确性提供了一定的参考。
(2) 配管管内制冷剂压力对配管结构会产生一定的预应力,由模态分析可知,考虑制冷剂平均压力后,配管系统各阶固频均有所提高,因此在进行仿真分析时,有必要考虑制冷剂压力对模态的影响。
(3) 从管路的振动位移云图来看,在压缩机工作频率下,配管系统的最大位移点在排气管U型弯位处,这为后期优化设计与减振方案提供了思路。
