基于灰色系统理论与ARIMA模型对涌水量预测研究

张润畦，商芷萱，蒋知廷，王 旭

(华北科技学院 安全工程学院，北京东燕郊 065201)

0 引言

我国煤矿水文地质条件极为复杂，煤矿水害是造成我国煤矿事故的一大重要因素。据统计，在过去的20多年里，有1094起矿井水害事故，死亡4426人，经济损失达亿元[1]，如图1所示。

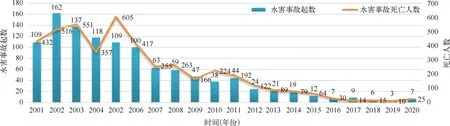
图1 近20年全国煤矿水害事故及死亡人数统计图

其中涌(突)水事故更是频繁多发，因此，为了避免事故的发生，应选取适当的方法对矿井涌水量进行预测，对煤矿安全生产有重要的实际意义。

随着国家对煤矿安全事业的投入，煤矿开采与生产过程中的设备、技艺、环境都有了极大的优化，矿井涌水量预测方法的创新速度也迅速发展[2]，初期提出了采用数学公式原理的比拟法和解析法，比拟法通常定义为以旧谋新，即利用某矿区原始涌水资料，谋划预测新采区的矿井涌水量的一种方法[3,4]；解析法中大井法最为出名，它是以矿井边界作为流量边界，把整个矿井的工作区概化为一个理想状态中的“圆形大井”[5,6]；随着数学知识的发展与计算机科学的进步，诞生了基于矿井水文地质概念模型，通过数值模拟软件，转化为数学模型的数值模拟方法[7]；随着研究发现，影响涌水量变化的因素之间也存在相互影响，它们相互耦合，相互关联，共同决定了涌水量的变化，通过研究其中的相互关系来对涌水量进行预测，形成一种新的方法，称之为相关分析法[8]；伴随着对涌水量预测的深入研究，发现影响其变化的因素太过于复杂，这些错综复杂的因素均表现为典型的非线性，因此，BP神经网络模型因其良好较强的抗干扰能力成为了一种主流方法[9]；为了实现通过少量已知信息预测未知信息，实现涌水量的短期预测，灰色系统理论应运而生[6,10]；后期研究发现，涌水量与时间存在明显联系，凭此建立起时间序列模型，近年来，时间序列模型频繁投入到矿井涌水量预测中，预测效果显著[11-13]。

为了满足煤矿对安全生产的要求，选取两种对水文地质参数的依赖性较小的方法进行对比。本文将对灰色理论GM(1∶1)模型和传统时间序列ARIMA两种方法进行分析，将实测值与预测值进行比较，分析二者的预测结果，以期找到更加适合涌水量预测的方法。

1 研究区概况

本文以山西平鲁后安煤矿实测涌水量资料整理得到的数据进行模型建立[14]，统计情况见表1。

表1 3年内矿井涌水量统计表

灰色系统理论通过Matlab建立GM(1∶1)模型拟合涌水量进行预测，时间序列模型通过SPSS建立传统ARIMA模型拟合涌水量进行预测。

2 灰色系统理论GM(1∶1)模型

2.1 预测步骤

2.1.1 数据检验与处理

(1)

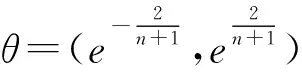
(2)

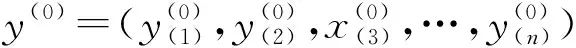
(3)

2.1.2 GM(1∶1)模型计算处理

(4)

之后生成均值序列：

(5)

式中，0≤α≤1，为权重。通常均值序列α=0.5。由此建立灰微分方程：

(6)

相应的GM(1∶1)白化微分方程为：

(7)

将灰微分方程移项得到：

(8)

式中，a,b为待定参数。上式可以写成矩阵的形式有：

(9)

即Xβ=Y。由最小二乘法可以确定参数矩阵β的估计值：

(10)

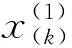
(11)

2.1.3 预测值检验

模型的预测效果通过精度的大小来判断，因此，检验过程就是要确定该灰色模型的精度是否符合要求[15]。

残差：

(12)

相对残差：

(13)

平均残差：

(14)

精度：

(15)

2.2 GM(1∶1)模型预测结果

本次模型的原始数据不满足级比检验，为使得模型可以运行，采取向右平移54个单位后(即c=54)再进行预测的方式，待预测结束后，将初步预测值去除54，即为最终预测值。

按表2标准评价精度等级[16]：

表2 精度判别表

GM(1∶1)模型预测结果见表3。

从表3可以看出，GM(1∶1)模型预测结果良好。

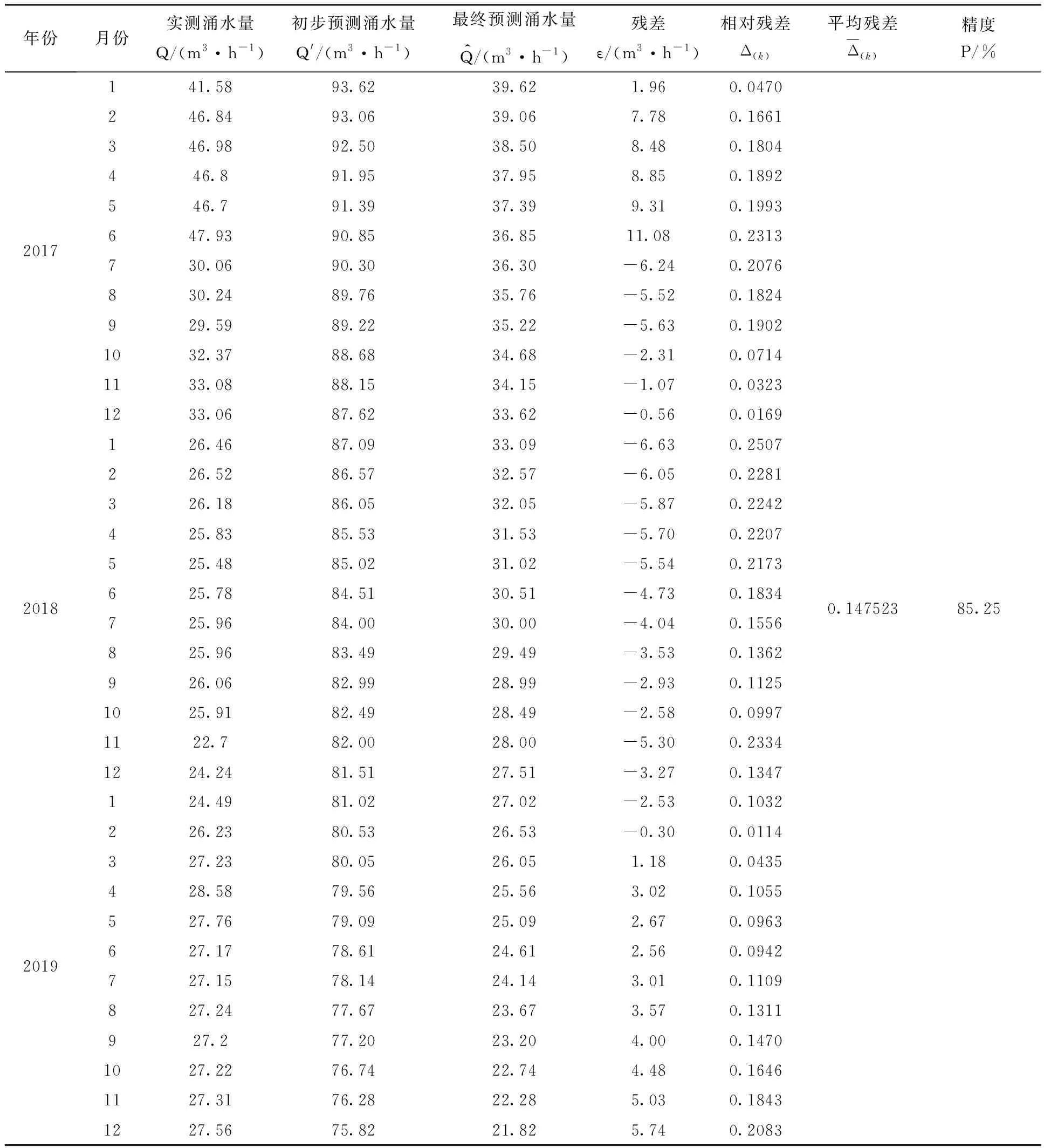
表3 GM(1∶1)模型误差分析

3 传统时间序列ARIMA模型

3.1 基本原理

本文采用ARIMA(p，d，q)模型，当p，d，q已知时，ARIMA的数学表示形式[17]为

(16)

式中，yt为t时刻y的预测值；φ为自回归系数；θ为移动平均系数；μ为常数；ζ为t时刻的误差。

3.2 建模步骤

3.2.1 平稳性检验

本文使用ADF检验，该检验用于稳定性检验，使用差分分析对数据进行稳定性处理，利用SPSS做出涌水量时间序列图，如图2所示。

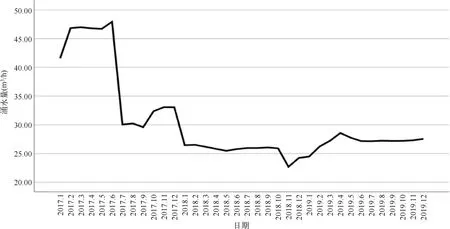
图2 原始涌水量时间序列图

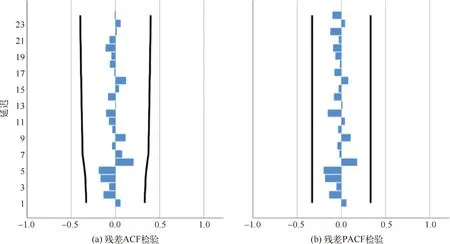
图3 残差检验结果图

从中可以看出原始数据为非稳定序列，在2017年6月份至7月份，发生大规模变化，因此需要通过差分运算进行校正。进行一阶差分后，进行平稳性检验，平稳性检验一般借助ADF检测[18]，通过查看ADF检验结果，根据分析t值，分析其是否可以显著性地拒绝序列不平稳的假设(P<0.05或0.01)。

检测结果见表4。本文通过EViews 11软件进行ADF检验，得到的显著性检验值t值为-6.584477，概率值p=0，证明该序列为平稳序列。

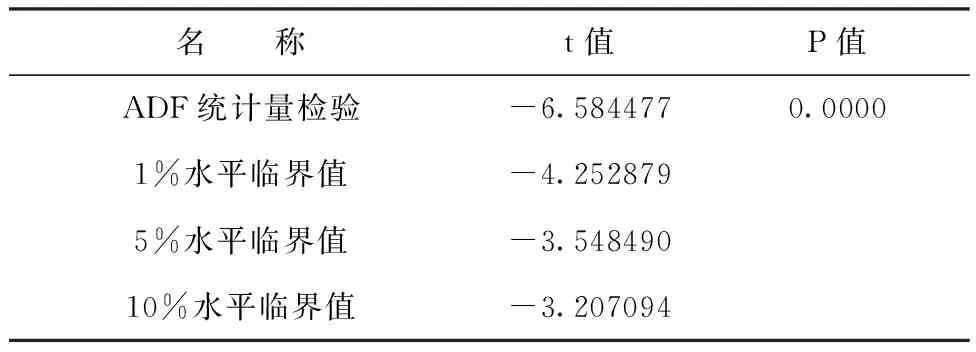
表4 ADF检验水平对应表

3.2.2 模型定阶及白噪声检验

查看差分前后数据对比图，判断是否平稳(上下波动幅度不大)，同时对时间序列进行偏相关分析，根据截尾情况估算其p、q值。

如图3所示，展示了自相关图(ACF)，包括系数，置信上限和置信下限。自相关图在q阶进行截尾，偏自相关图(PACF)拖尾，ARMA模型可简化为MA(q)模型。

本模型最终确定p，d，q均为1时，对残差进行检验，该序列通过了白噪声检验，时间序列模型拟合效果较好。

3.3 ARIMA模型预测结果

根据拟合结果，确定自回归系数为0.524；移动平均系数为-0.651，常数为-0.573。由此建立不考虑相关因素的传统ARIMA模型：

yt=0.524yt-1-0.651ζt-1-0.573

(17)

预测结果与实测数据拟合曲线如图4所示。

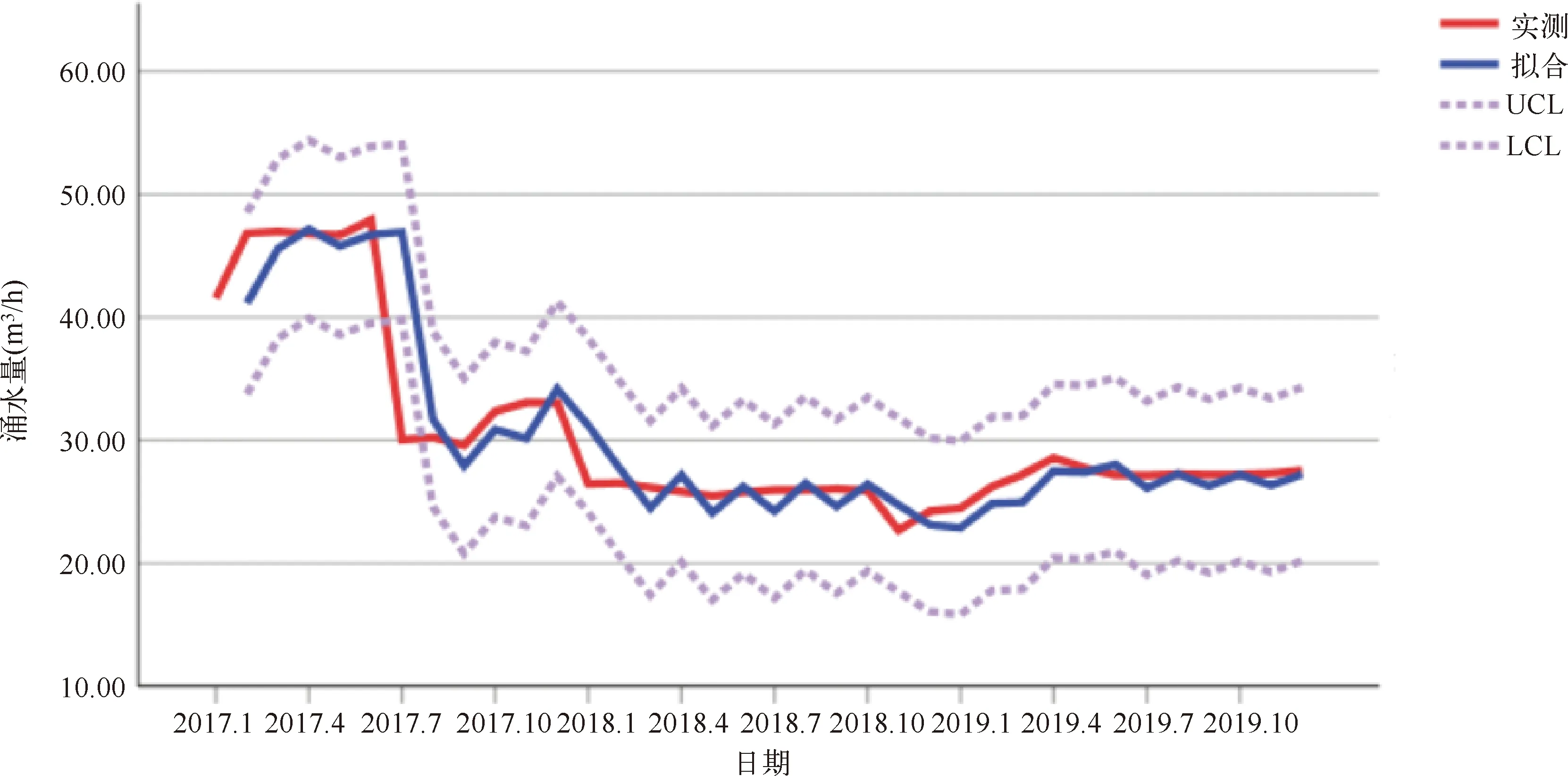
图4 实测数据与预测数据对比图

通过实测数据与预测数据对比可知，前期数据差异悬殊，拟合效果一般，中后期预测值与实测值差异较小，拟合曲线与实测曲线基本重合，说明拟合效果良好。

4 两种模型结果对比分析

4.1 数学评价方法

本文采用平均绝对值误差方法对两种模型进行评估比较。

平均绝对误差：

(18)

式中，f(xi)为样本预测值；yi为样本实际值；m为总样本数。

4.2 评价结果

基于建立的GM(1∶1)模型与ARIMA模型，回代入原始数据，与实测涌水量进行对比，结果见表5。

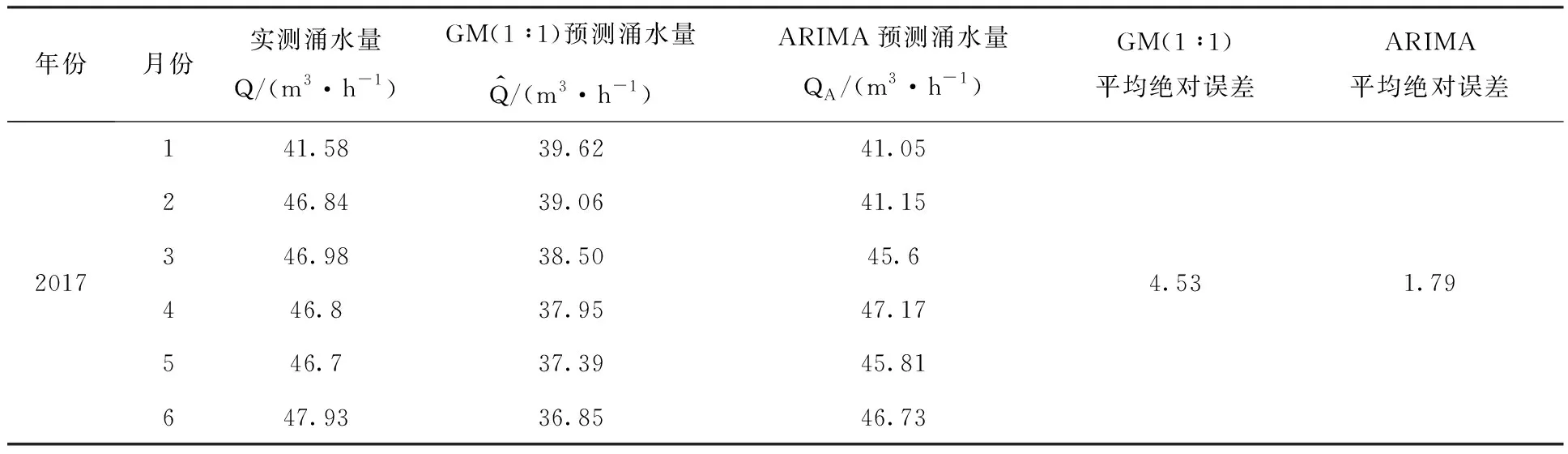
表5 两种方法误差对比

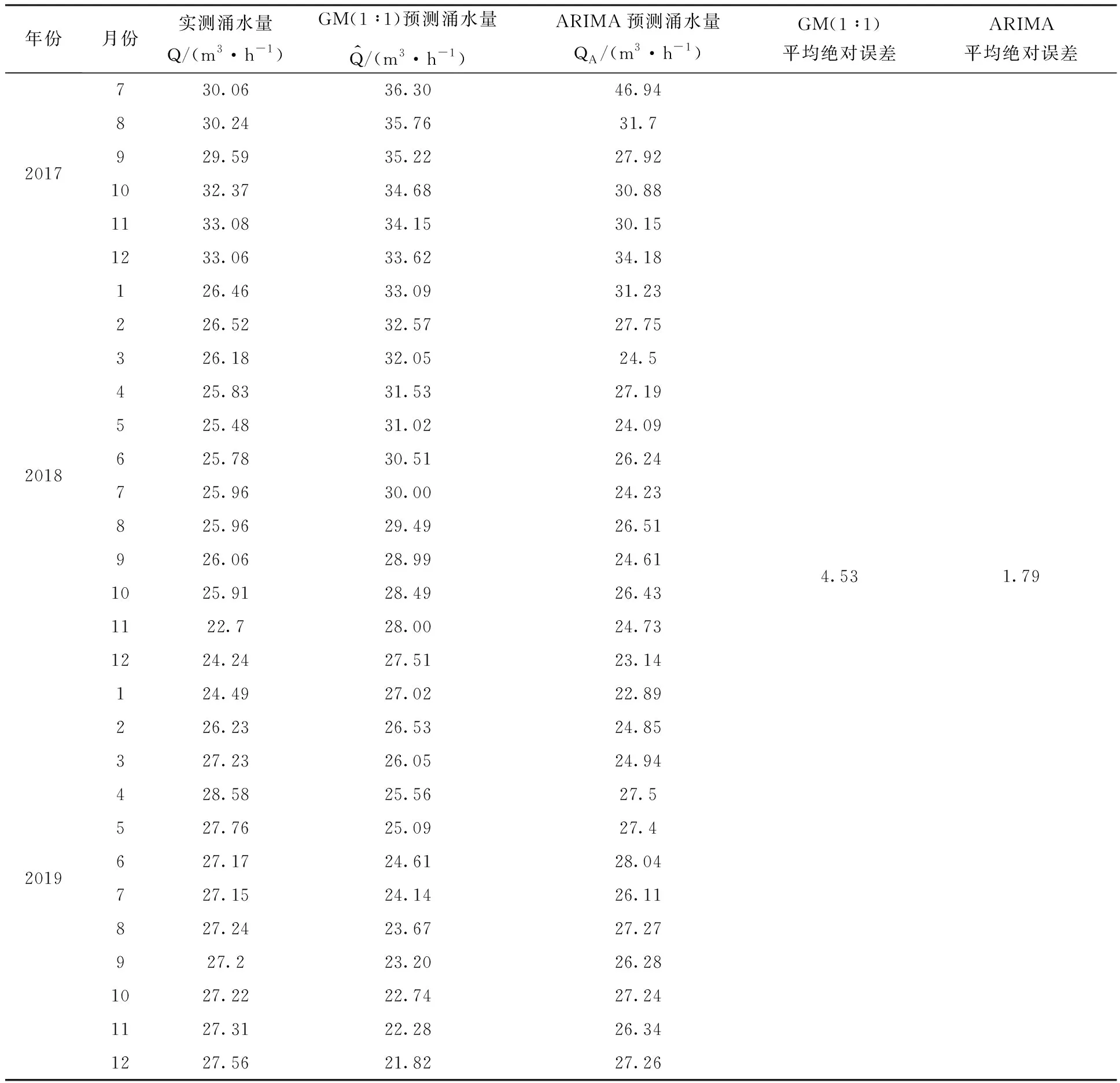
续表

由表5可以看出，GM(1∶1)模型平均绝对误差为4.53，ARIMA模型平均绝对误差为1.79，从数值关系上推断，ARIMA模型平均每个预测值与实际值之间上下浮动值小于GM(1∶1)模型，ARIMA模型预测效果良好。

4.3 拟合效果对比

如图5所示，GM(1∶1)模型呈线性下降趋势，无明显波动，未体现出充分的规律性，与实测涌水量变化曲线拟合效果不佳，与实测值相差较大；而ARIMA模型与实测涌水量相比，呈现出轻微滞后效应，变化曲线围绕实测涌水量曲线上下小规模浮动，拟合效果良好。

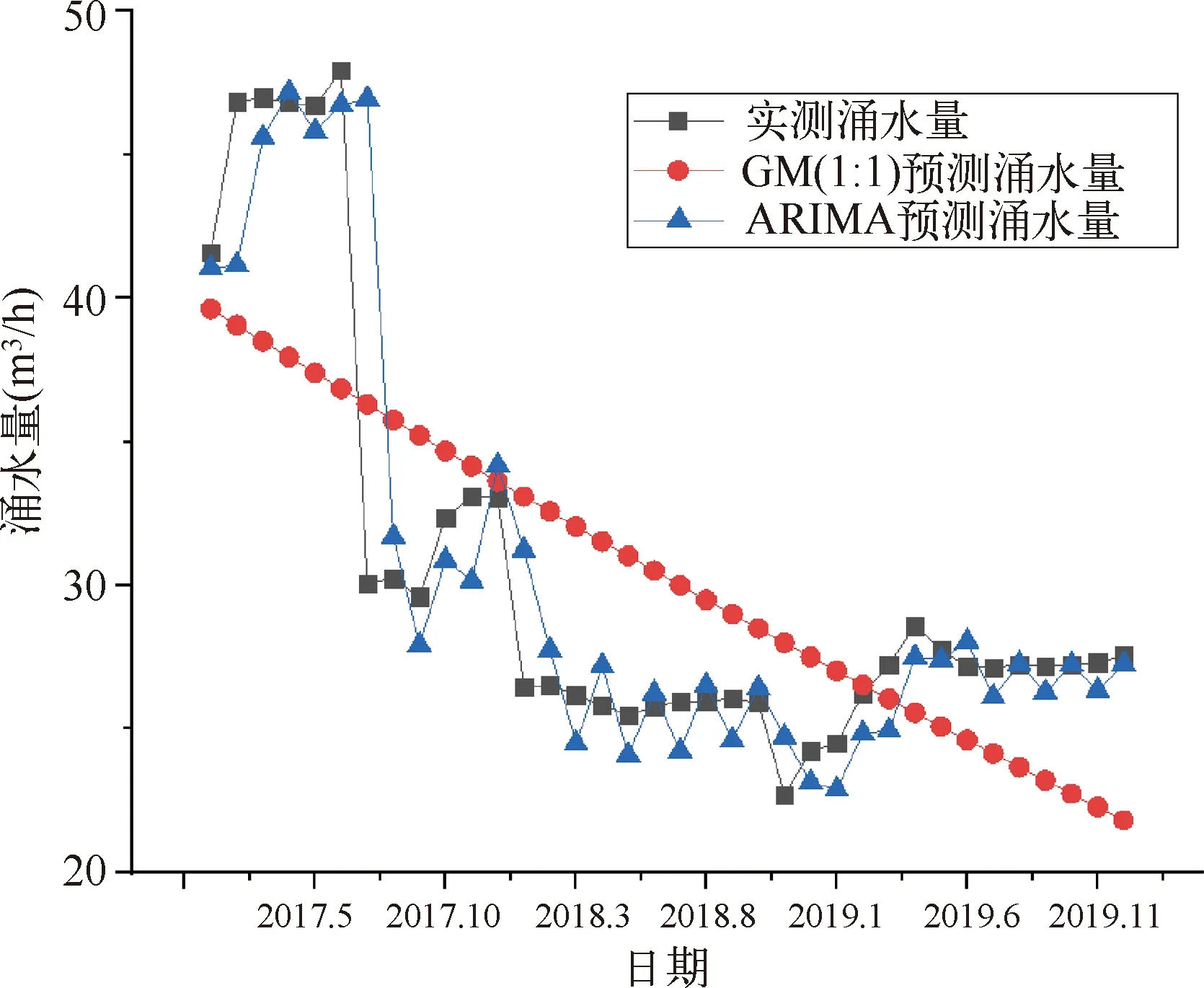
图5 模型拟合结果

5 结论

(1) 矿井涌水量是一个受多因素影响的非线性系统，仅靠单一因素分析其变化规律是不可行的。研究表明，灰色系统理论GM(1∶1)模型与传统时间序列ARIMA模型相比，传统时间序列ARIMA模型预测效果更佳。

(2) 灰色系统理论GM(1∶1)模型仅适用于短期预测和指数变化类型，对于波动程度较大的类型，其预测效果一般，并不适用于本类型煤矿涌水量预测。

(3) 通常所采用的数学建模参数估计方法计算过程均较为复杂，本文基于SPSS与Matlab软件进行建模分析，简化了繁琐的计算，使模型更加直观简便，便于应用。

(4) 若要对涌水量进行准确预测，应考虑更多影响因子，例如：降水量、地形、地质构造等。为了能够精准预测，未来应建立多因素综合预测模型，扩大对影响因素的考究，进一步提高模型的适用程度与预测精度。