寡头竞争下航线网络选择的动态博弈模型

景崇毅，卢 燕，吴孟瑶

（中国民航飞行学院经济与管理学院/机场管理与工程研究中心，广汉 618307）

0 引言

国际经验表明，布局合理的航线网络能够极大地提升整个国家的民航运输效率，对推动民航运输生产发展和国家综合交通运输系统建设具有重要的战略意义。民航十四五规划提出要构建布局完善、高效率运行的航空运输网络体系。以国际枢纽和区域枢纽机场为支点，构建高联通、广覆盖、便捷经济的国内航线网络，不断提升网络整体效应。对于航空公司而言，航线网络是航空公司生存和发展的基础，是提高自身竞争力的有效途径，它不仅受到宏观管理政策、区域发展环境、航线网络模式的影响，同时也受到市场需求状况、供给分布以及竞争环境等诸多因素的影响，是一项非常重要且复杂的战略决策。研究航线网络决策问题具有重要的现实意义和理论价值。

国外学者对航线网络选择的课题已有一定的研究成果。Kawasaki考察了一家航空公司在考虑需求方网络效应和旅客时间价值异质性的情形下，如何选择航线网络结构。Alderighi等在博弈论框架下讨论了航空公司航线网络结构的设计问题。Barla和Constantatos研究了在一个三航点网络中需求不确定性对垄断航空公司网络结构的影响。Oum等通过一个三城市网络上的双寡头博弈，分析放松管制后航空公司之间的战略互动对其网络选择的影响。Barla和Constantatos采用古诺静态博弈模型研究了需求不确定性和竞争对航空公司网络结构选择的影响。Aguirregabiria和Ho基于动态博弈模型从需求、成本和战略角度研究了美国的枢纽轮辐式网络。Zhe建立了一个不同于Barla和Constantatos的三阶段网络竞争模型，分别包括：网络结构决策、航班频率决策、产品定价决策。该模型主要从实证的角度分析航空公司合并的网络效应，以及网络外部性对网络结构的影响。Lin研究了两家枢纽公司通过建立子公司开展网络竞争的问题。Silva等基于双寡头模型，考虑拥堵外部性、航班频率、中转成本及枢纽区位等因素，研究了航空公司的网络竞争策略，同时还分析了监管者如何通过机场定价引导航空公司构建最优的网络结构。Babić和Kalić研究了双寡头竞争环境中航空公司如何选择航线网络结构，模型中考虑了产品差异化、航班频率、运力大小及平均航程等因素。Yang等建立一个双层规划模型，从动态交互的角度研究了寡头竞争市场中航空公司如何设计最优航线网络的问题，并利用台湾航空市场数据进行验证。Ciliberto和Zhang利用美国航空业数据检验了三个不同的市场进入模型：同时进入博弈、无战略威慑的进入博弈、有战略威慑的进入博弈，结论是现实数据最契合有战略威慑的进入博弈模型。Lordan等研究了不同商业模式的航空公司的网络鲁棒性，发现低成本航空的网络鲁棒性优于全服务航空。Ren利用静态进入博弈模型研究美国西南航空进入某网络后对其他航空公司支付函数和进入概率的影响。

国内学者对航线网络选择问题的研究并不充分，大多数研究集中在基于优化模型的网络设计问题。如柏明国等利用最短路优化算法求解枢纽网络的设计问题。邓亚娟等建立了需求不确定有容量限制的枢纽航线网络设计模型。高荣环和杨芳研究了竞争环境下枢纽航线网络的优化设计方案。乐美龙等基于机场容量包络曲线构建了随机需求下多分配、非严格的两阶段混合整数随机规划网络模型。李实萍在多个外部选择、多个市场以及双寡头竞争的环境下，通过构建航线网络结构选择的决策模型，研究网络结构的不同组合对航空公司竞争绩效的影响。汪瑜等针对市场补贴定价决策对航空公司枢纽航线的网络设计影响，基于双层规划思想，分别构建航空公司枢纽航线网络设计的上层规划模型和各民用运输机场空运市场补贴定价决策的下层规划模型。

通过以上文献梳理，我们发现目前关于航线网络选择的研究还存在两方面的不足：第一，理论假设与决策现实不符。现有研究一般基于静态博弈模型，即假定竞争者同时决策，或者即使没有同时决策，但后来者无法观察到在位者的决策结果，这与现实并不相符。现实中一般是某家航空公司首先进入某个市场，后进入者可以观察到在位者的网络及运力配置状况。从博弈的角度看，在位者也必然要考虑到后进入者的存在性及其可能采取的策略。为了更加贴合这种决策现实，本文采用Stackelberg动态博弈模型进行分析。第二，对不确定性的设定存在局限性。为了贴合这种决策现实，本文不仅考虑了单一市场本身需求的不确定性，还考虑了不同市场之间的相关性所导致的不确定性。

1 构建三阶段博弈模型

1.1 问题表述和参数说明

在图1所示的包含三个城市的航线网络中，已有一家在位航空公司，现另有一家航空公司将要进入该网络与其进行竞争。该城市网络中存在一个枢纽城市和两个非枢纽城市和。、和为航段。当通过枢纽网络飞行时，只需通过一个航段来完成一次旅行的旅客被称为本地市场，而需通过两个航段（和）来完成一次旅行的旅客被称为中转市场。对点对点网络而言，中转市场指的是原先只能通过枢纽网络进行中转的旅客。在本文中，将采用枢纽网络的航空公司称为“枢纽航空公司”，采用点对点网络的航空公司称为“非枢纽航空公司”。模型相关参数如表1所示。

图1 双寡头航空公司在三航点网络中的竞争示意图

表1 模型相关参数及含义汇总

续表1

我们将航空公司战略决策划分为三个阶段，在每一阶段，航空公司都进行一场完全信息下非合作的动态博弈。后进入的航空公司能够观察到在位航空公司选择的策略，故而后进入航空公司能够利用这些信息做出更理性的决策。三阶段决策内容分别如下：

第一阶段：需求未知时，航空公司选择航线网络结构：枢纽网络()或点对点网络()。

第二阶段：需求仍未知下，航空公司进行运力决策。运力投入是一项长期决策，取决于航空公司拥有的飞机数量、机场可用登机口和起降时刻的数量。如果在第一阶段选择了枢纽网络，那么航空公司将决定同时为本地和中转市场提供的运力；如果选择了点对点网络，航空公司将分别确定为本地和中转市场提供的运力。“运力”一词是指每家航空公司每条航线每周或每月能提供的最大座位数量。我们假定运力成本取决于网络结构，由于枢纽航空公司需要更多的枢纽资源投入和更复杂的调度管理，因此c＞c。

第三阶段：需求已知后，基于前两个阶段已经确定的网络结构和运力，航空公司参与Stackelberg数量博弈。本文中的“数量”是指受运力限制的航空公司每周或每月提供的实际座位数量。在需求明确后的第三阶段，枢纽航空公司仍然可以在本地市场和中转市场之间分配运力，而非枢纽航空公司却没有这样的灵活性。第三阶段的博弈是两个市场的动态竞争，航空公司争夺中转旅客和本地旅客。

通过逆推归纳法来求解博弈均衡。在需求不确定性解决后，航空公司在第三阶段的问题是已知在位航空公司的运力和网络结构的情况下，选择数量q(=1,2)来最大化π。由于航空公司的运营成本主要与总座位数有关，旅客的边际成本很小，可以忽略不计，因此将其视为零。在第二阶段运力博弈中，航空公司在给定网络结构的情况下，确定均衡运力。最后在第一阶段博弈中，航空公司考虑到在位航空公司的网络结构决策，根据预期利润∏来确定自身的网络结构。此外，为了确保航空公司在市场上的非负利润，令c≤u/2和c≤u/2。

1.2 模型创建

已知在位航空公司（公司1）的网络结构，新进入航空公司（公司2）有两种网络结构选择（或）。新进入航空公司的最佳响应网络结构可以通过图2所示的博弈树来确定。

图2 航空公司网络结构的序贯博弈示意图

如果航空公司采用的是枢纽网络，那么它在第二和第三阶段的问题可以分别表示如下：

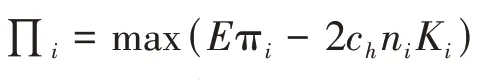
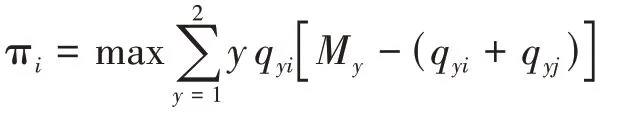
如果航空公司采用的是点对点网络，那么它在第二和第三阶段的问题可以分别表示如下：

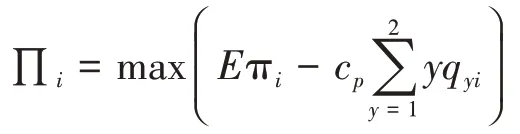
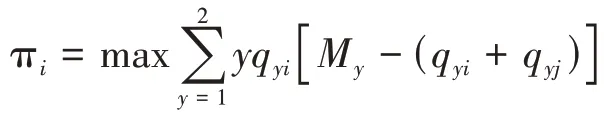
因为枢纽航空公司在第三阶段决策中仍然可以在本地市场和中转市场之间分配运力，因此，当双寡头博弈中有枢纽航空公司参与时，仍需将运力博弈和数量博弈单独分析，即该博弈仍是三阶段博弈。只有当两家航空公司都采用点对点网络时，三阶段博弈才退化为两阶段博弈。

1.3 假设条件

（1）为了简化分析，假设本地市场是对称的。市场、具有共同的需求函数，并且三个市场、和都是双向对称的，即从到的流量与从到的流量具有相同的特性。

（2）枢纽航空公司总是服务于中转市场（文献［6］中所述）。

（3）每一家航空公司都耗尽了它的运力（文献［5］和［11］中所述）。对于枢纽航空公司来说，+=n K；对于非枢纽航空公司来说，q=n K。强加假设（2）和（3）的目的是为了使市场出清，模型的分析处理更清晰明了，但并不会影响基本结论。

2 航线网络决策的博弈分析

我们通过比较航空公司在运力博弈中的预期利润来对网络结构博弈均衡进行分析。

2.1 博弈分析

首先根据第三阶段的Stackelberg博弈确定座位数量，在此基础上计算均衡运力，最后比较不同网络结构下的利润函数，以确定采用何种形式的网络结构。

表2和表3分别给出了寡头航空公司网络博弈的均衡运力及均衡利润，其中，第一、二项表达式分别表示在位航空公司和新进入航空公司的均衡运力及均衡利润。

表2 寡头垄断情形下航空公司动态博弈的均衡运力

表3 寡头垄断情形下航空公司动态博弈的均衡利润

证明：在假设条件下，以在位航空公司采用点对点网络，新进入航空公司采用枢纽网络为例进行证明，通过逆推归纳法求解均衡运力和利润。其余三种情况的证明与其类似。

（1）新进入航空公司(=2)在数量博弈中的利润如下：

通过分别求解关于和的一阶条件，解得：

该航空公司在运力博弈中的利润如下：

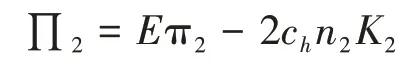
将和代入后，求解关于的一阶条件，解得：

因为后进入的航空公司在选择数量之前会观测到在位航空公司的数量，因此会根据在位航空公司投入的数量来选择自己的数量。将代回和后，会得到新进入航空公司关于在位航空公司数量的反应函数，即：

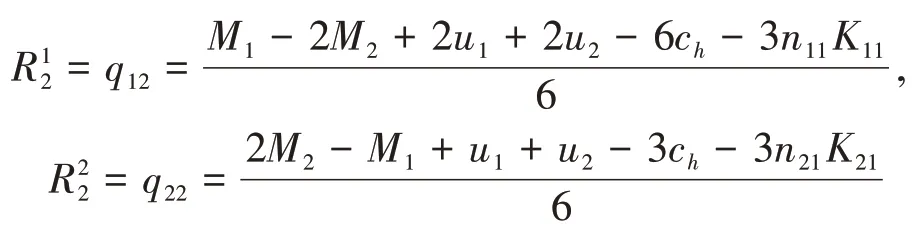
（2）在位航空公司(=1)在数量博弈中的利润如下：

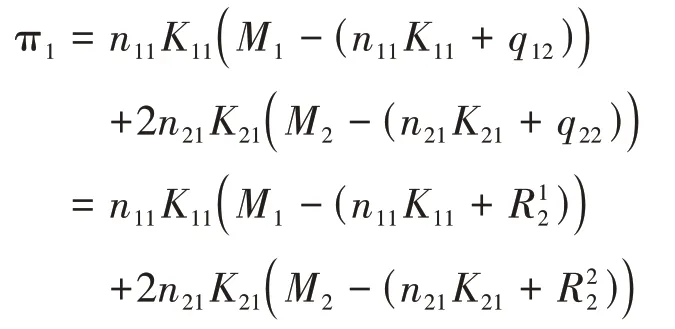
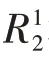
分别求解关于和的一阶条件，解得：

之后均衡运力及利润便可求出。

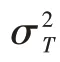
2.2 均衡网络分析

考虑到在位航空公司的网络结构，我们现对新进入航空公司最佳的响应网络进行分析。通过表3推导出以下命题。

命题1：

（i）如果在位航空公司采用枢纽网络，则满足以下条件时，新进入者的最佳响应网络是枢纽网络：

（ii）如果在位航空公司采用点对点网络，则满足以下条件时，新进入者的最佳响应网络是枢纽网络：

证明：（i）在位者采用枢纽网络时，令Δ∏=∏-∏＞0，

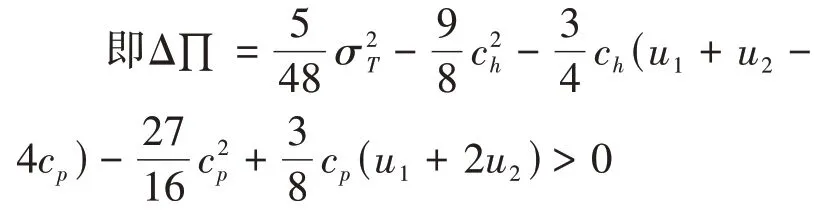
（ii）的证明与（i）类似。

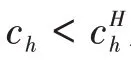
3 结语

本文运用动态博弈理论，研究了完全信息下双寡头航空公司的航线网络选择问题。为此，我们构建了一个三阶段动态博弈模型。在第一阶段，航空公司首先确定自己的网络结构；第二阶段，在需求未知下，航空公司确定投入的运力；第三阶段，需求已知后，利用Stackelberg模型，分析双寡头航空公司的数量博弈。通过逆推归纳法求解整个博弈的均衡解。

本文所使用的动态博弈模型考虑了市场不确定因素，通过假定市场上的需求符合线性逆需求函数p=M-(q+q)来实现，通过该需求函数，可以设定市场不确定性，不仅考虑了单一市场本身需求的不确定性外，还考虑了不同市场之间的相关性所导致的不确定性。而一般的动态博弈只是假定逆需求函数为p=-(q+q)，其中一般为常数，因此如果选择一般的动态博弈模型进行分析，则无法研究市场不确定性对航空公司网络结构选择的影响，以及市场规模对航空公司运力配置决策产生的影响。

基于假定条件，我们得到了双寡头航空公司博弈的均衡运力、均衡利润。研究发现，非枢纽航空公司在某市场上的均衡运力仅取决于该市场需求均值，而枢纽航空公司的均衡运力会受到两个市场需求均值的影响。市场不确定性为枢纽网络提供了巨大的灵活性价值，在竞争环境下，这种灵活性价值仍然存在。新进入者的最佳网络决策实质上是权衡灵活性价值和成本优势。当单位运力成本较低时，新进入者更倾向于获取灵活性价值，此时采用枢纽网络。