基于CFD的双褶数滤袋阻力特性的数值模拟

鲁进利，何 杰，庄乾双，钱付平，王 佳

(1. 安徽工业大学 a. 建筑工程学院; b. 能源与环境学院, 安徽 马鞍山 243032；2. 苏州恒清环保科技有限公司, 江苏 苏州 215600)

工业生产过程中产生的颗粒物、SO2、NOx等大气污染物严重危害人类健康，对其进行的排放治理成为工业生产过程中的重要环节。袋式除尘器具有收集效率高的优势，尤其对细颗粒物分离表现突出(过滤效率>99.99%)[1]，是实现超低排放的主流设备，在打赢蓝天保卫战中发挥着举足轻重的作用[2-3]。

褶式滤袋是在传统圆形布袋的基础上将一定长度的滤料折叠成褶形成的袋状过滤元件。由于褶式滤袋在有限空间上具有较大过滤面积的明显优势，相比于常规滤袋更受青睐[4]。当前国内外学者的研究主要聚焦于褶式滤袋本身结构参数对压降的影响。Theron等[5]结合数值和实验方法研究3种不同褶高和褶宽对褶式纤维过滤器压降和流场的影响，实验发现压降随着褶宽变大和褶高变小而减小，紧密和高褶皱会在滤料表面形成较大的速度梯度。Fotovati等[6]比较矩形褶和三角褶对压降的影响，证明颗粒在惯性较小时，三角褶引起的压降比矩形褶的要小；相反大颗粒高速过滤时，矩形褶优于三角褶。方璨等[7]通过数值模拟研究不同褶皱率的5种褶数及3种袋长对褶式滤袋除尘器的阻力特性和流场均匀性的影响,研究表明褶数N=12(褶皱率ɑ=1.12)的褶式滤袋的过滤阻力最小，袋长为3 m时压力和速度分布更均匀。Velali等[8]比较4种不同的褶皱重建方法，结果表明，流动阻力主要在滤筒的膜内部和褶皱中有显著影响。吴利瑞等[9]、Kim等[10]研究褶形结构在滤芯形成滤饼后变形和堵塞对过滤面积的影响，实际有效过滤面积只占50%～60%。过滤面积是影响除尘设备选型的因素之一，除尘器多孔介质颗粒的堵塞和过滤面积的减少会增加其压降，从而使除尘器的风机能耗增加[11-13]。还有相关研究发现涡流的形成和气流的集中会影响除尘器的除尘效果。Pereira等[14]分析4种不同入口位置对袋式除尘器能量效率的影响，发现实际中应避免气流再循环，以确保通过袋式过滤器表面的质量流量的均匀分配，从而减少能量损失。提高除尘器气流分布的均匀性，提高滤袋使用寿命，有效降低运行维护费用[15]。Rocha等[16]研究发现单个入口会产生高速区域导致滤袋高磨损和高压降，3个入口的过滤区域更均匀，表明更均匀的气体质量流量分配可有效减小压降。除尘器的过滤压降是过滤介质两端的压降与褶皱通道引起的压降之和，褶皱过滤介质表面的流场分布对预测过滤压降至关重要。

由上述可知，目前关于沿轴向褶式滤袋表面的压降分布规律研究还鲜有报道。基于此，本文中通过数值模拟研究除尘器不同入口速度和不同褶数对褶式滤袋轴向过滤压降分布的影响规律。鉴于单一褶数滤袋存在过滤压降分布不均匀的特性，提出一种新型组合式双褶数滤袋，如图1所示。滤袋的上半部褶的数量N为10和下半部褶的数量N为8不同，考虑到上下部褶数不同连接错位，因此结合处通过相同直径的圆环结构相连，褶皱处缝隙用滤料缝合。研究新型组合式双褶数(N=10&8)滤袋内外静压分布的强度和均匀性，并与常规褶式滤袋进行比较分析。新型组合式双褶数滤袋的研究可为除尘器结构优化、提高滤袋使用寿命和降低运行能耗提供理论参考。

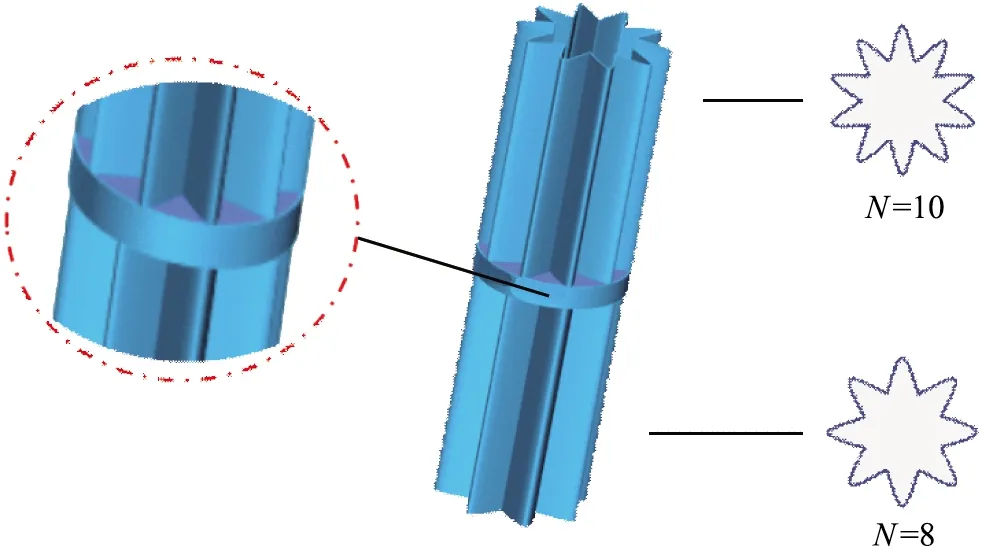
图1 新型组合式双褶数滤袋结构

1 数理模型

1.1 几何模型及网格划分

图2所示为褶式滤袋除尘器的结构模型和网格模型。由图2(a)可知褶式滤袋除尘器的结构和气流流向，模型的简化只考虑褶式滤袋除尘器入口至出口之间的气流流动，忽略连接件以及起固定作用的其他零部件的影响。整个模型主要由过滤室、灰斗和净气室3个箱体部分组成，圆形进风管连接灰斗，净气室上方连接圆形出风管；过滤室为长方体结构，褶式滤袋垂直悬挂于过滤室中。含尘气体通过灰斗侧部的进风管以下进风的方式进入到过滤室中，经滤袋过滤后进入到净气室，再由出风口排出。图2(b)为常规褶式滤袋和双褶数滤袋的简化模型，考虑到双褶数滤袋结构的复杂性，网格划分方式采用非结构，定义网格的边界，对滤袋部位的网格进行局部加密来提高计算精度，双褶数连接处局部加密。褶式滤袋的袋长l=1 050 mm，褶皱外直径D=324 mm，褶皱内直径d=180 mm。图3所示分别为单一褶数N=8(模型-1)，上褶数为10、下褶数为8(N=10&8，模型-2)，单一褶数N=10(模型-3)的3种滤袋模型。

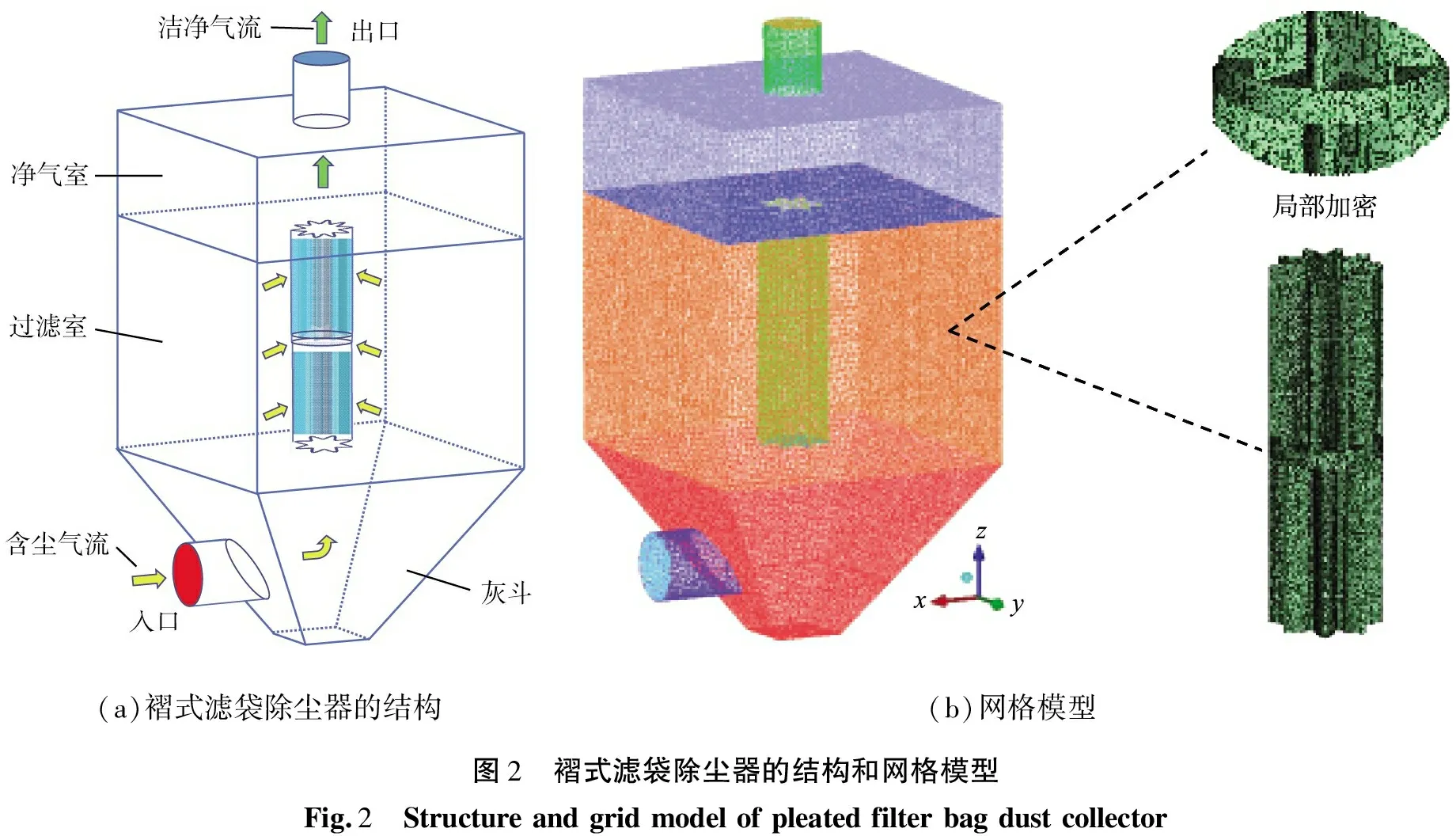
(a)褶式滤袋除尘器的结构(b)网格模型图2 褶式滤袋除尘器的结构和网格模型Fig.2 Structureandgridmodelofpleatedfilterbagdustcollector

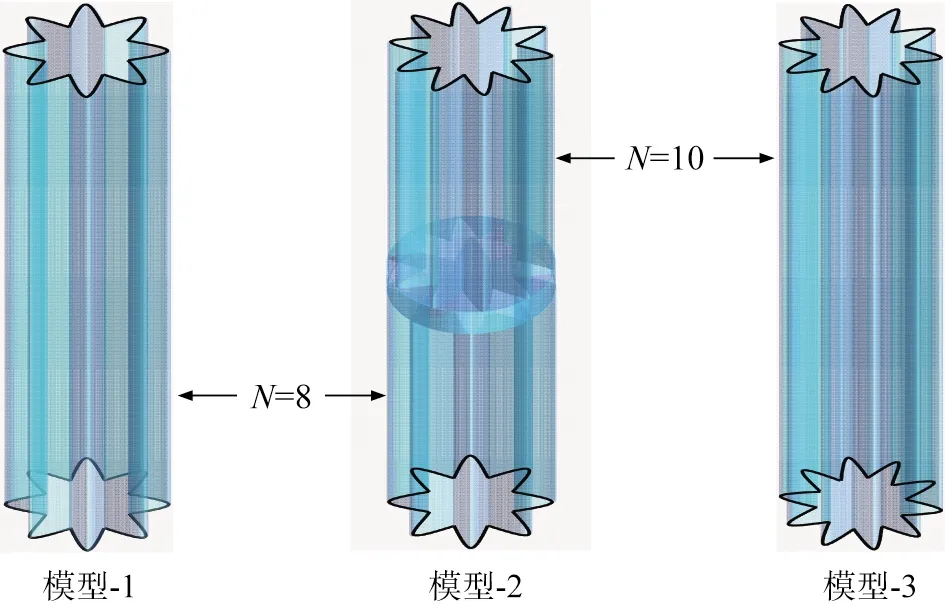
图3 褶式滤袋和双褶数滤袋的模型结构

1.2 计算模型和边界条件

假定流体是不可压缩、稳态、等温的湍流运动。进入除尘器的气流近似单相流，内部各物性参数各向同性，采用标准k-ε模型[17]。主要结构参数和用于数值模拟的主要边界条件如图4所示。对于流场的模拟，采用基于压力-速度耦合的SIMPLE算法，除尘器入口设置为速度入口，除尘器出口设置为压力出口，出口压力为1×105Pa。将灰斗、花板、袋底和所有箱体均设置为固体壁面，采用“无滑移”边界条件，近壁区运用壁面函数法计算[18]。褶式滤袋属于薄膜状多孔介质，因此可将滤袋介质看作一维简化模型，其边界条件设置为多孔跳跃模型(porous jump)；与多孔介质建模相关的系数可根据描述褶式滤袋内部径向流动的动量方程Darcy公式[19]来确定,

(1)

式中：v为流体径向速度，m/s；K为介质的渗透系数，m2；μ为流体的黏度，Pa·s；p为压降，Pa；r为介质厚度，mm。设置边界条件时，将介质厚度r设置为2 mm，渗透系数设置为6.5×10-11[20]。3种模型的各个工况下的模拟参数如表1所示。

表1 各工况的模拟条件

图5给出了褶式滤袋上均匀布置的6个压力监测点位置，高度方向上从滤袋的底部到袋口依次为测点1—6。相邻测点间距h=150 mm，3种褶式滤袋模型的各压力测点布置相同。

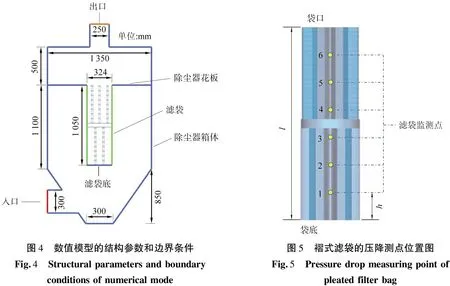
图4 数值模型的结构参数和边界条件Fig.4 Structuralparametersandboundaryconditionsofnumericalmode图5 褶式滤袋的压降测点位置图Fig.5 Pressuredropmeasuringpointofpleatedfilterbag

1.3 模型验证

为消除网格数对模拟结果的影响，需验证网格无关性，分别对网格数为89.3万、97万、107.5万、115.8万、125.4万、148.3万、194.5万的7种模型进行模拟计算，选取进出口质量流量差作为监测数据。图6所示为除尘器进出口质量流量差随网格数的变化，当网格数超过107.5万时的差值波动很小，即改变网格数量对模拟结果的影响已可忽略不计。为了保证模拟计算的精确度和有效降低计算时间成本，本研究中模型划分的网格数为107.5万，网格质量均达到0.37以上。

图6 进出口质量流量差随网格数的变化

为验证多孔跳跃模型和标准k-ε模型的可行性，依据文献[21]建立单个滤袋袋式除尘器结构模型，所得压降模拟值与文献中滤袋直径为160 mm和长度为3 000 mm的针刺毡滤袋的压降实验值进行对比。如图7所示，过滤压降的具体数值的变化趋势与文献结果基本吻合，误差在±8.69%以内，表明本文中所用多孔跳跃模型和标准k-ε模型的合理性。

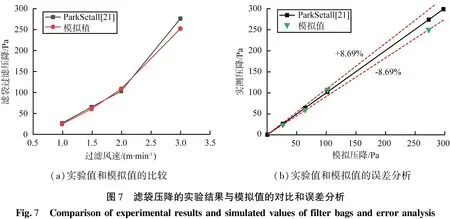
(a)实验值和模拟值的比较(b)实验值和模拟值的误差分析图7 滤袋压降的实验结果与模拟值的对比和误差分析Fig.7 Comparisonofexperimentalresultsandsimulatedvaluesoffilterbagsanderroranalysis

2 结果与分析

图8所示为入口风速v5=18 m/s时不同褶数滤袋xoz截面(y=0)的压力云图,其中图8(b)—(d)分别为3个模型的压力云图，其他入口风速vi情况压力分布基本相似，此处不再列出。由图8(b)和(c)可知，褶式滤袋内部的压力沿轴向分布不均匀。靠近袋口处的内外静压差明显大于靠近袋底处，且沿滤袋轴向从袋底到袋口呈梯次增加变化。主要原因是褶式滤袋在过滤过程中，其袋口为洁净气体出口，气体不断流出，导致滤袋内外压差变大，从而使得褶式滤袋上的压降分布存在一定差异。入口风速vi相同时，N=8和N=10情况下压力轮廓彼此相似。由图8(d)可知，双褶数滤袋内部的压力沿轴向从袋底到袋口相对呈现平滑变化。此外，当入口风速相同，双褶数滤袋轴向方向上的内外静压差变化小于常规褶式滤袋的，表明双褶数滤袋上、下部褶数的不同可使得整个滤袋轴向静压差分布更均匀，以确保通过滤袋表面的流量均匀分布，避免气流的集中，可以提供更低的压降。

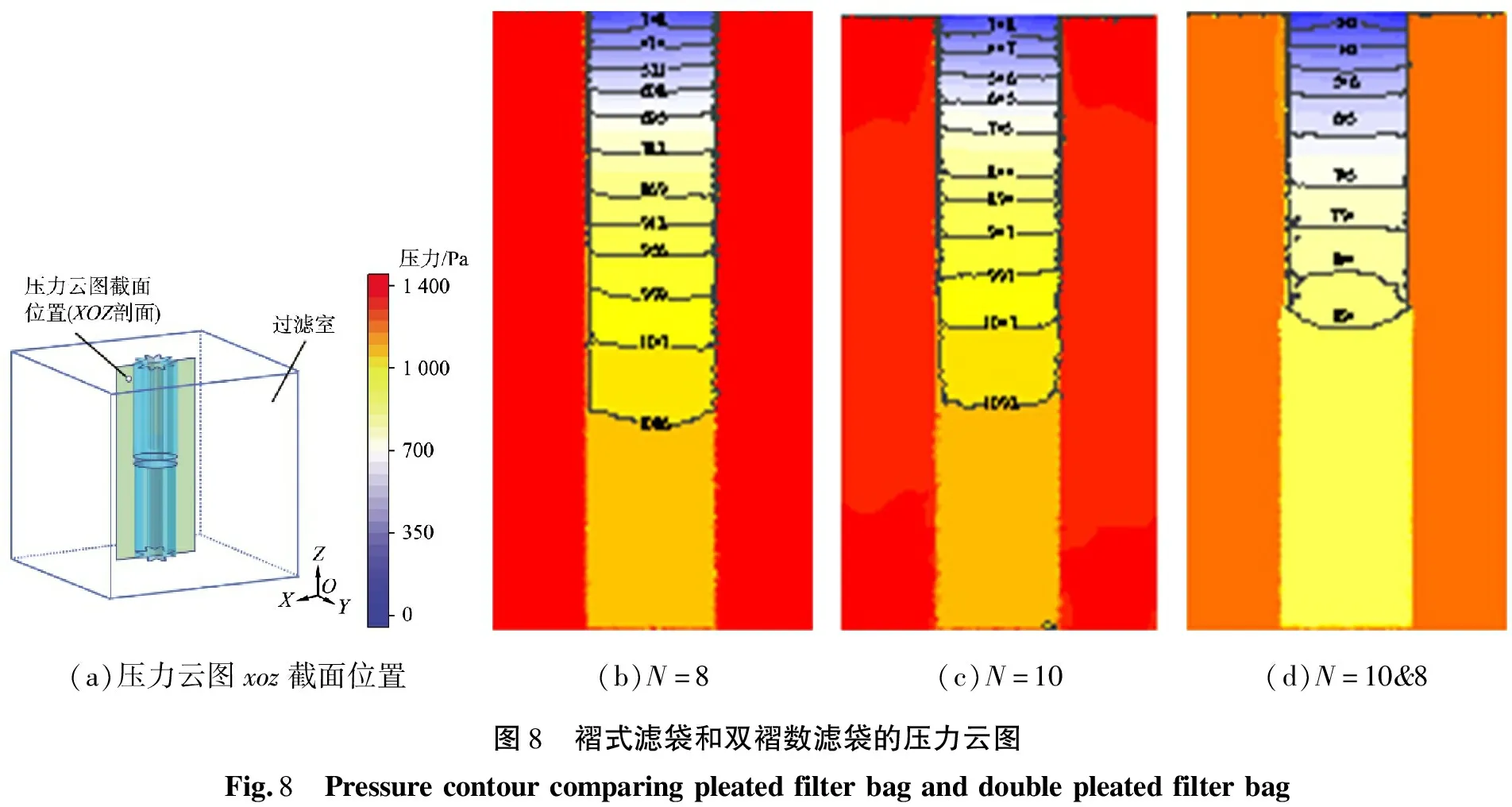
(a)压力云图xoz截面位置(b)N=8(c)N=10(d)N=10&8图8 褶式滤袋和双褶数滤袋的压力云图Fig.8 Pressurecontourcomparingpleatedfilterbaganddoublepleatedfilterbag

图9所示为5种入口风速对应的褶式滤袋轴向压降变化情况，图中纵坐标表示各测点压降值，横坐标表示测点沿滤袋轴向上的高度h。由图可知，褶式滤袋上半部分各测点的压降明显大于下半部分的，且越靠近袋口位置的压降越大，从袋口到袋底呈非线性降低趋势。测点1—3(垂直位置的下半部分)的压降值变化较小，测点3—6(垂直位置的上半部分)的压降值变化较显著。表明褶式滤袋的压降主要发生在滤袋的出口处，底部的压降很小。由图9(a)可知，对于褶数N=8、入口风速v1=10 m/s的压降曲线，靠近袋底高度h1(测点1)处的压降为217 Pa，靠近袋口(测点6)处的压降为357 Pa，测点间的压降差为140 Pa。当入口风速增大到18 m/s，测点1处的压降为282 Pa，测点6处的压降为772 Pa，2个测点压降差为490 Pa。从压降差值的变化和压降曲线的弯曲程度分析得出，随着入口风速变大，褶式滤袋的压降分布越不均匀。由此可知，入口风速是影响压降的重要参数之一。由图9(b)可知，褶数N=10褶式滤袋的压降曲线，不同褶数N的褶式滤袋均呈现出类似的压降分布不均匀性现象。区别在于，图9(b)中滤袋褶数的增加使得过滤面积增大，当入口风速相同时，N=10的各测点的压降值比N=8要相对较小。针对上述现象，从而模拟出新型组合式双褶数滤袋。

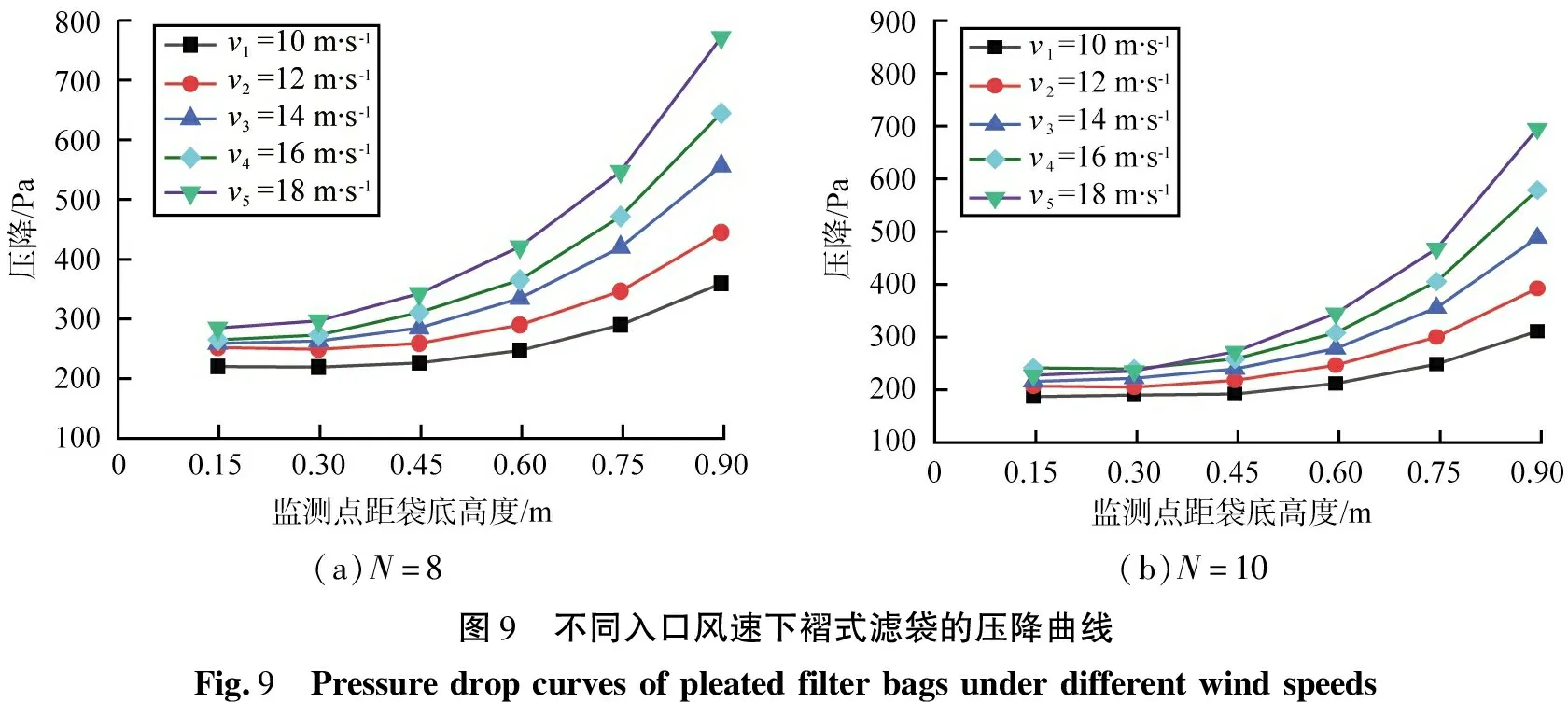
(a)N=8(b)N=10图9 不同入口风速下褶式滤袋的压降曲线Fig.9 Pressuredropcurvesofpleatedfilterbagsunderdifferentwindspeeds

图10所示为N=10&8的双褶数滤袋在5种入口风速下各测点的压降变化情况。入口风速v1=10 m/s，测点1处的压降为196 Pa，测点6处的压降为317 Pa，二者相差121 Pa。相比褶数N=8的滤袋，测点1、6之间的压降差降低了13.6%，表明双褶数滤袋可使袋底到袋口的压降值波动变小，靠近袋口的测点6的压降值比褶数N=8的滤袋降低了11.2%。当入口风速v5=18 m/s，测点1、6的压降分别是263、653 Pa，二者差值为390 Pa。相比褶数N=8的滤袋，测点1、6的之间压降差降低了20.4%，靠近袋口的测点6的压降降低了15.4%。上述数据对比分析表明，新型双褶数滤袋的特殊结构对滤袋的压降分布产生较大的影响，缩小袋底压降和袋口压降之间的差值，压降分布更均匀。

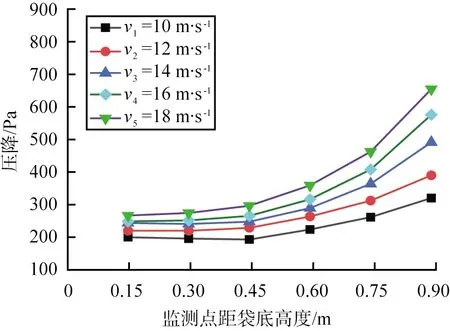
图10 N=10&8的双褶数滤袋的压降曲线

为进一步论证压降分布的不均匀性，引入不均匀度η和相对标准差S0这2个无量纲参数来反映褶式滤袋轴向上各位置压降的不均匀程度。不均匀度η用于描述各个测点上压降的不均匀，相对标准差S0表示为滤袋各测点位置的压降与各测点平均压降的离散程度，其值越小，表示压降分布的越均匀。具体公式如下：

(2)

(3)

图11所示为3种滤袋各测点的不均匀度和相对标准偏差。由图11(a)—(c)可知，3种滤袋的不均匀度都随着入口风速的增大而逐渐增大，表明除尘器的处理风量越大，滤袋上的压降分布越不均匀。靠近袋口位置的测点6(h=0.9 m)的不均匀度最大(距不均匀度0的距离)。当入口风速v5=18 m/s时，褶数N=10相较于褶数N=8滤袋测点6不均匀度增加16%。N=10&8的双褶数滤袋测点6不均匀度相较于N=8、10分别减小了5%和18%。图11(d)所示为不同入口风速时3种滤袋的相对标准差S0。从相对标准差的角度分析，随着入口风速的变大，相对标准差S0数值增大，压降分布的均匀性变差。在相同的入口风速下，双褶数滤袋的相对标准差比常规褶式滤袋的要小，且在入口风速vi=18 m/s时，双褶数滤袋压降相对标准差比另外2种常规褶式滤袋分别减小了7%和18%，压降分布的均匀性显著提升，表明新型双褶数滤袋有效改善滤袋过滤过程中的压降分布的不均匀性，随着处理风量的增加，几何结构参数对压降的影响更明显。

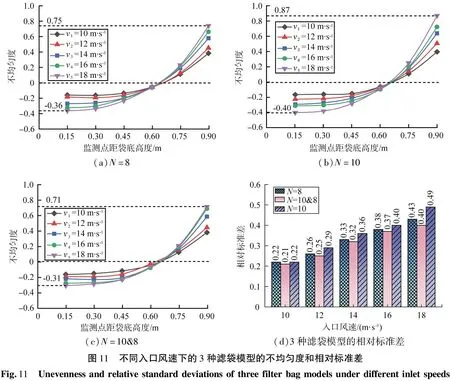
(a)N=8(b)N=10(c)N=10&8(d)3种滤袋模型的相对标准差图11 不同入口风速下的3种滤袋模型的不均匀度和相对标准差Fig.11 Unevennessandrelativestandarddeviationsofthreefilterbagmodelsunderdifferentinletspeeds

图12所示为不同入口风速下3种滤袋模型对除尘器进出口的过滤压降的影响。从图中可以看出，除尘器进出口过滤压降均随入口风速的增大而变大。相比褶数N=8和褶数N=10的滤袋，双褶数滤袋的过滤压降在不同入口风速下都有所减小，最大降幅为13.5%。因双褶数的特殊结构可以有效降低褶式滤袋压降分布的不均匀性，即新型滤袋上半部褶数的增加，过滤面积增大使得气体流量分配更均匀。压降分布越均匀导致更低的过滤阻力，从而减少能量损失。

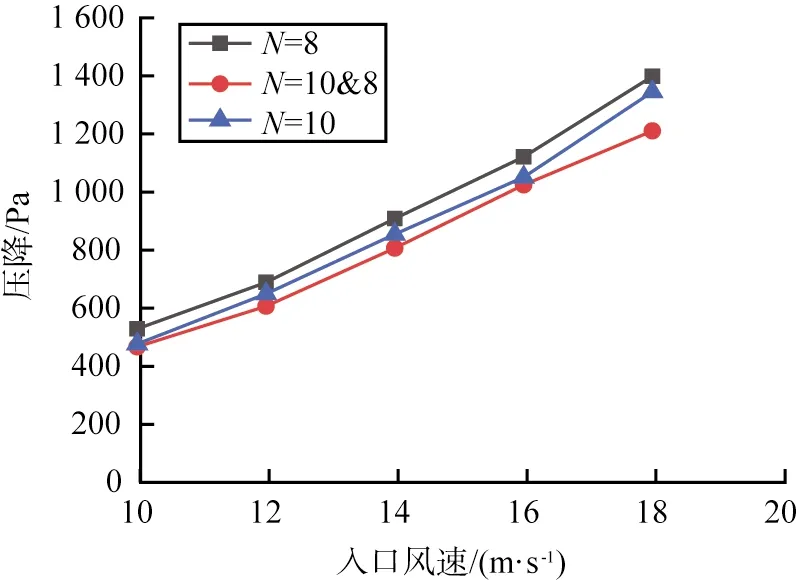
图12 除尘器进出口过滤压降随着入口风速的变化曲线

3 结论

1)褶式滤袋在过滤过程中，靠近袋口上半部的压降明显大于靠近袋底下半部的，且越靠近袋口位置压降越大，与滤袋顶部相比，底部的压降较小，从下到上呈现非线性增大趋势；入口风速是影响压降分布的重要参数之一，滤袋顶部的压降随着入口风速的增加而增加，表明风量越大，压降分布越不均匀。

2)不同褶数的褶式滤袋上下串联在一起的组合结构对滤袋的压降分布产生较大的影响，缩小了袋底压降和袋口压降之间的差值，压降分布更均匀，在入口风速为10 m/s的条件下，与褶数为8的滤袋相比，双褶数滤袋的顶部和底部压降差降低了13.6%，当入口风速增至18 m/s时，两者压降差降低了20.4%，表明双褶数的结构能确保滤袋具有更均匀的压降分布。

3)随着入口风速的增加，常规褶式滤袋和双褶数滤袋的不均匀度和相对标准差都逐渐变大。相比常规褶式滤袋，双褶数结构有效降低了压降分布的不均匀性，其进出口过滤压降在各风量下都有所降低，最高降低了13.5%，从而可有效降低除尘器能耗。