基于BP 神经网络的沙柳地上生物量预测模型

程冀文，王树森＊，罗于洋，张 岑,2

(1. 内蒙古农业大学沙漠治理学院，荒漠生态系统保护与修复国家林业和草原局重点实验室，内蒙古 呼和浩特 010018；2. 清水河县老牛湾镇人民政府 内蒙古 呼和浩特 011614)

沙柳（Salix psammophilaC.Wang et Ch.Y.Yang）又名北沙柳，在库布齐沙漠有广泛分布，常作固沙造林树种[1-2]，也是我国北部地区防风固沙的优良树种和当地典型的能源树种[2-3]。通常情况下，沙柳在沙丘中下部有少量分布，在滩地沙区大量密集分布[4]。沙柳具备生长速率较快的特点，并且人工栽培沙柳在短时间内就能产生体积很大的灌丛，因此能够在水土保持与荒漠化防治、水源涵养、气候调节等生态效益方面起到重要的作用[5]。由于沙柳木质优良，还可以广泛用于造纸、人造板等工业用途[6]。

在干旱半干旱风沙区，沙生灌木有着防风固沙、水土保持等作用，通常野外调查使用的直接收割法会对地表造成破坏从而发生土壤侵蚀现象[7]。因此探究灌木生物量与易测因子间的关系，建立沙生灌木生物量模型对沙生灌木生物量研究有很大的助力。目前，国内外学者在生物量模型方面有大量的研究[8-10]，通常选取林木因子作为自变量构建灌木生物量模型，但是由于各区域之间自然环境条件的巨大差别，以及不同气候区灌木植被的形态特性等具有很大不同，因此很多地区灌木的生物量预测模型仅在当地有较好的解释力。因此对于灌木构建适应其生境的生物量预测模型是十分必要的[11]。

近年来，许多学者将BP 神经网络应用在林业上[12-14]。研究发现，BP 神经网络模型精度相较于传统更好[15-19]。但是目前的研究大多集中在高大乔木的生物量估算方面，对于运用BP 神经网络进行灌木，尤其是沙生灌木的生物量估算却鲜有报道。因此，利用沙柳的不同林木因子建立BP 神经网络生物量估算模型，探究BP 神经网络在沙生灌木生物量方面的应用是必要的。本研究以库布其沙漠沙柳为研究对象，建立了沙柳BP 神经网络的生物量预测模型，探究不同林木因子对沙柳BP 神经网络生物量预测模型的影响，以期为沙柳以及其他沙生灌木生物量建模与估测工作提供参考依据。

1 材料与方法

1.1 研究区概况

研究区域地处库布齐沙漠，处于鄂尔多斯市杭锦旗独贵塔拉镇境内，地理坐标为108°15′～108°24′ E ，40°48′～40°39′ N ，属于典型温带大陆性干旱、半干旱季风气候。年均降水量约400 mm[20]。其范围内木本野生植物主要有小叶杨（Populus simoniiCarr）， 沙 枣（Elaeagnus angutifoliaLinn）， 沙 柳（Salix psammophilaC.Wang et Ch.Y. Yang）等[6]。

1.2 研究方法

1.2.1 数据采集 外业数据采集时间为2017 年4 月。在研究地选择迎风坡风蚀、丘间低地沙埋和未沙埋3 种立地条件，共选择91 株沙柳。根据沙柳的形态学特性，选取用于BP 神经网络生物量预测模型建模的因子有丛高（H）、地径（D）、冠幅（C）、基部分支数（Nt）、单枝最大分支数（Nb）、单枝最大分枝次数（Nbt）、枝条粗度（Db）、芽眼数（Ne）。采用皮尺和游标卡尺对以上林木因子进行测量和记录（表1）。记录工作结束后，将所选取的沙柳齐地面刈割，使用电子天平现场称取鲜质量。将现场刈割的沙柳枝条带回实验室使用烘箱70℃烘干24 h 至恒质量，使用天平称取干质量，计算沙柳地上部分生物量。

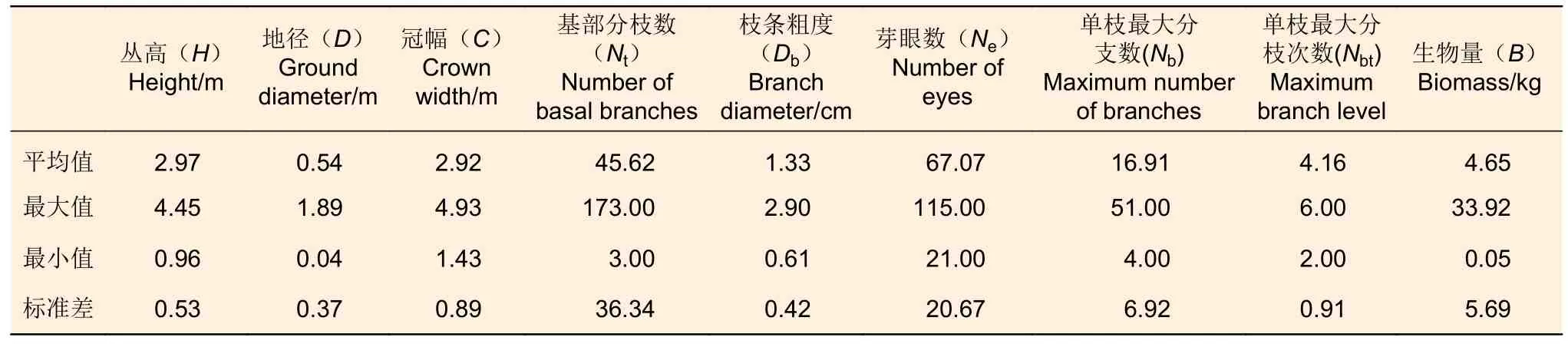
表1 建模数据统计Table 1 Summary statistics for model modeling and validation

1.2.2 BP 神经网络 BP 神经网络由包括输入层、隐层和输出层共3 部分组成（图1），BP 神经网络中神经元结构如图2 所示，x1～xn(1, 2,3, ···,n)为输入信号，ω1～ωn(1, 2, 3, ···,n)为权重，b为偏置，∑为求和节点，σ为激活函数。按照Kolmog-orov 定理，单隐层的BP 神经网络将能够无限接近任意连续的非线性曲线[21]。但过分拟合会导致模型的泛化能力差，所以在实际的应用中还要结合样本本身的特性来控制拟合程度。

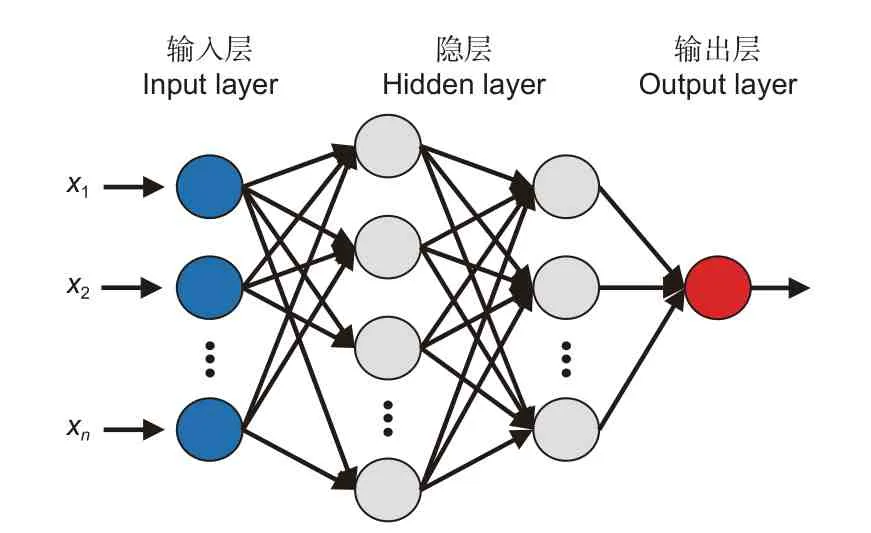
图1 BP 神经网络结构Fig. 1 Structure of BP neural network

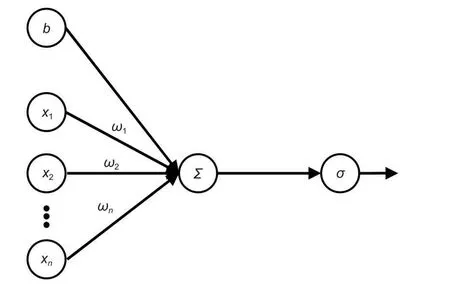
图2 神经元结构Fig. 2 Neuron structure

1.2.3 BP 神经网络模型的建立 构建沙柳BP 神经网络生物量预测模型使用Matlab 软件中的nntool 工具箱，以沙柳林木因子作为输入层，沙柳生物量实测值为训练目标。为确定BP 神经网络的隐层节点数的经验公式，其中：Nh为隐层节点数，Nin为输入层节点数，Nout为输出层节点数，对比其估测精确度及泛化能力以确定最佳隐层节点数。建模时，设置目标精度为0.001，最大迭代次数为1 000，学习率为0.01，隐层传递函数为logsig，输出层传递函数为purelin，使用后的模型训练算法为L-M 算法。

1.2.4 归一化处理与反归一 对于参与建模的数据采取归一化处理，可以让神经网络的训练效率有所提升，并且在拟合后还必须对输出数据采取反归一处理，使输出数据重新转换回沙柳的生物量的输出值。据此，本研究通过下列公式对输入因子数据和输入目标数据进行归一化处理：

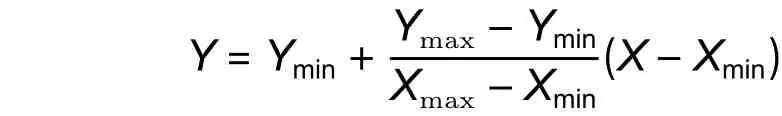
式中：X为未进行处理的值；Xmax、Xmin为代表未进行处理数据组中的最大和最小值；Y为进行处理后的值；Ymax和Ymin分别为进行处理后的数据组中的最大和最小值。

当BP 神经网络拟合结束后，对所得数据进行反归一处理，也就是将程序运行得到的数据映射到实际预测值。

1.2.5 模型评价与检验 采用决定系数R²，均方根误差（RMSE）和平均绝对误差（MAE）对模型性能进行评价。

2 结果与分析

2.1 模型输入因子的筛选

前期可供作为输入因子的备选指标有丛高（H）、地径（D）、冠幅（C）、基部分支数（Nt）、单枝最大分支数（Nb）、单枝最大分枝次数（Nbt）、枝条粗度（Db）、芽眼数（Ne），对各因子与生物量（B）之间进行相关性分析，结果如图3 所示。

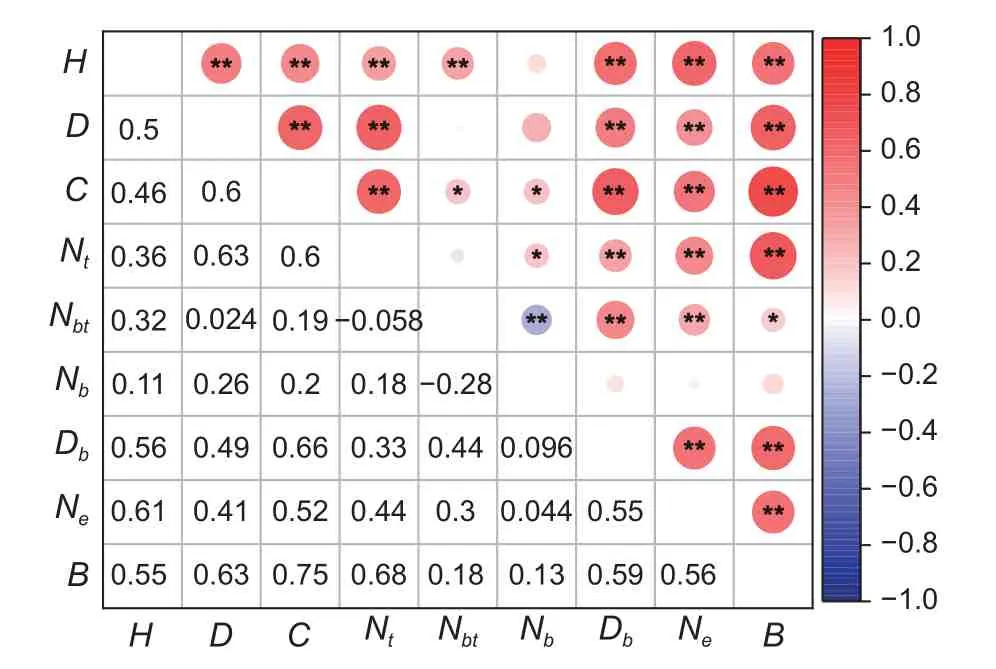
图3 沙柳各因子相关性分析Fig. 3 Relationship of factors inSalix psammophila

其中各因子与生物量相关性表现为：冠幅（ 0.751） ＞基 部 分 支 数（ 0.677） ＞地 径（ 0.631） ＞枝 条 粗 度（ 0.589） ＞芽 眼 数（0.555）＞丛高（0.550）＞单枝最大分枝次数（0.179）＞单枝最大分枝数（0.132），其中丛高、地径、冠幅、基部分支数、芽眼数、枝条粗度与生物量间表现为极显著相关（P＜0.01）；单枝最大分枝次数与生物量间表现为显著相关（P＜0.05）；单枝最大分枝数与生物量之间显著相关。由此选取丛高、地径、冠幅、基部分支数、芽眼数、枝条粗度为模型最终输入因子。对于传统生物量模型而言，将丛高、地径、冠幅、基部分支数、芽眼数、枝条粗度分别作为自变量拟合生物量模型。对于BP 神经网络模型而言，根据其相关性高低逐个加入模型输入层，确定输入层为输入因子数为1～6。

2.2 BP 神经网络模型的建立

根据相关性大小，共设置6 组输入变量Nin分别为1～6。输出变量Nout为生物量。由于输出值都为1，输入变量为1～6，则根据经验公式可得，当输入因子数为1 时，BP 神经网络隐层数Nh的取值范围为2.41～11.41之间；当输入因子数为2～5 时，BP 神经网络隐层数Nh的取值范围最小值为2.73～3.45，隐层数Nh的取值范围最大值为11.73～12.45；当输入因子数为6 时，BP 神经网络隐层数Nh的取值范围为3.65～12.65。由于神经网络训练结果有一定的波动，为增加模型的容错率，则将隐层数Nh选取为整数，当输入因子数为1 时，BP 神经网络隐层数Nh的取值范围为2～11 的整数；当输入因子数为2～5 时，BP 神经网络隐层数Nh的取值范围为3～12 的整数；当输入因子数为6 时，BP 神经网络隐层数Nh的取值范围为4～13 的整数。对不同输入因子数各10 隐层的模型分别训练10 次，不同输入变量拟合情况见表2。

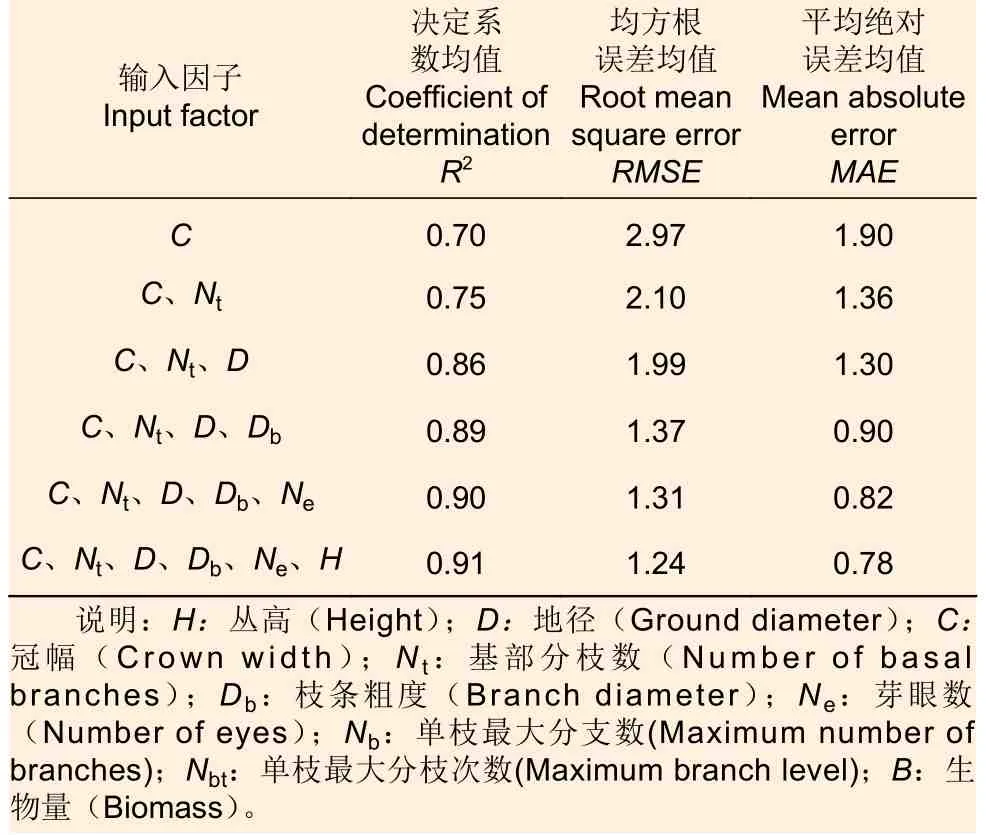
表2 BP 神经网络模型不同输入变量拟合优势度评价Table 2 Evaluation of fitting dominance of different input variables in BP neural network model

可以看出，模型的精度随着输入因子个数的增加而增加（图4），当输入因子数量为5 时，模型精度相比输入因子数量为4 时提升不明显，为了平衡模型的易用性和精度，则选择4 输入因子为模型的最优输入变量数。

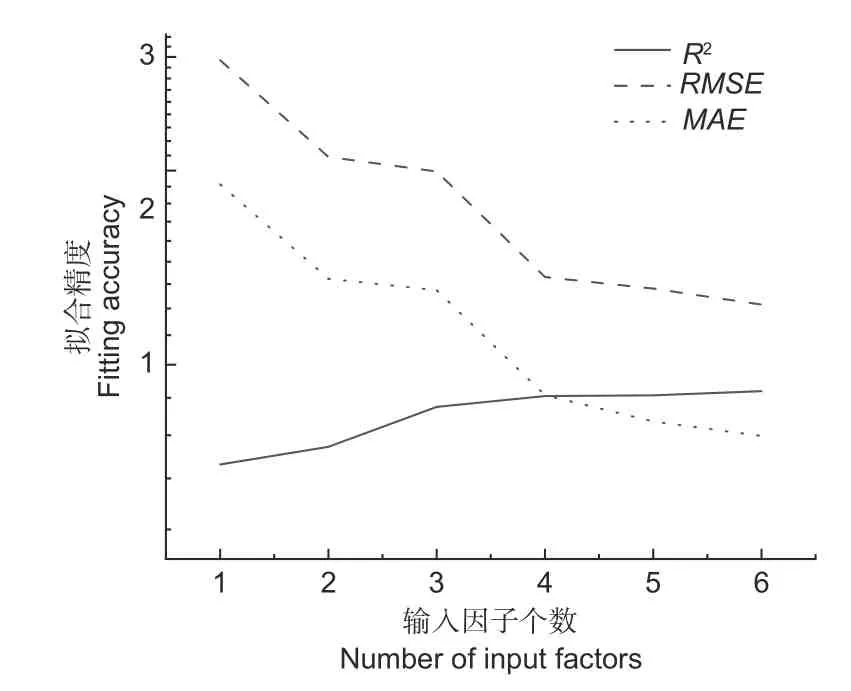
图4 随着输入因子增加模型性能变化Fig. 4 Fitting accuracy with different number of input factors

2.3 BP 神经网络最优模型的确定

当输入因子数为4 时BP 神经网络隐层数Nh的取值范围为3～12 的整数，不同节点数的模型拟合情况(见表3)，其中当隐层数为9 时，其R2在各隐层数中表现为最大，RMSE和MAE表现为最小，由此得知，当隐层数为9 时，模型拟合效果最好。

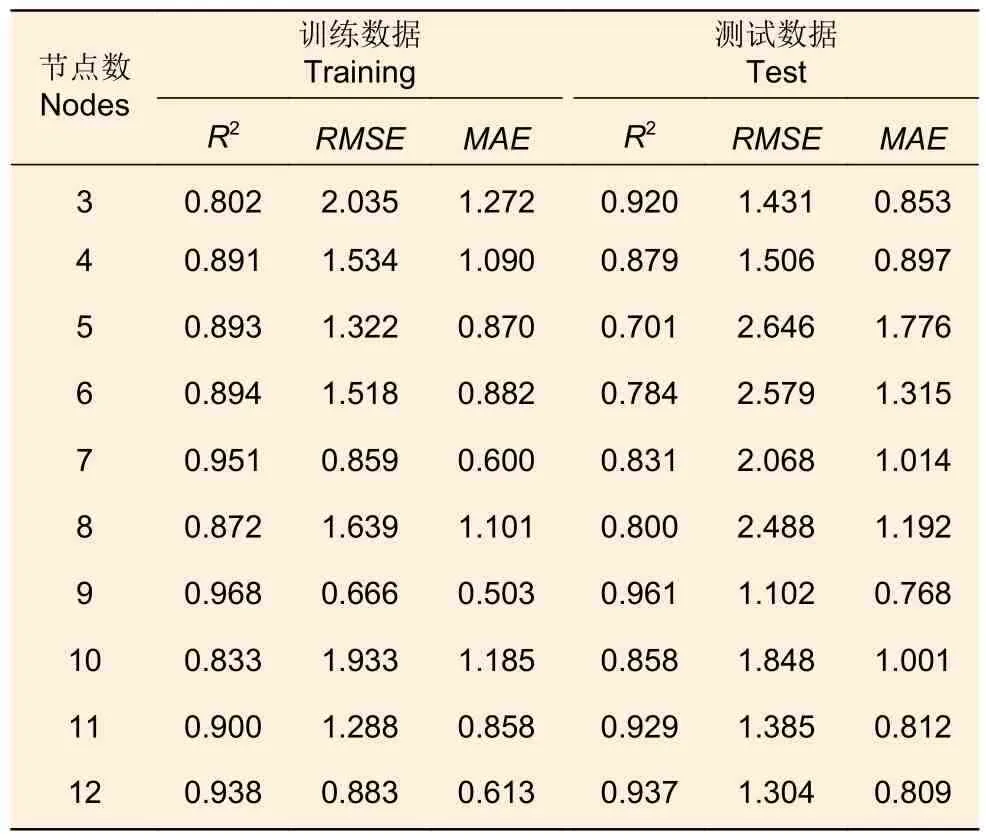
表3 输入因子数为4 时BP 神经网络模型拟合优势度评价Table 3 Evaluation of fitting dominance of BP neural network model when the Ninfactors is 4

由此，最佳输入变量和最佳隐层数确定后，在同一个隐层节点数的基础上不断训练模型，最终选择合适的结构为最后的模型，其中：最优结构[输入层节点数(Nin)∶隐层节点数(Nh)∶输出层节点数(Nout)]=4∶9∶1。经过训练所得传递函数模型为：

H= purelin (1.506 1h1+ 1.151 6h2+ 0.226 53h3−1.447 2h4−0.234 79h5+ 1.225 4h6−1.263 5h7−0.155 27h8−2.062 6h9−0.853 28)；

h1= logsig (0.844 89C+ 1.865 2Nt+ 3.207 6D−4.063 2Db+ 6.167 7)；

h2= logsig (6.942C+ 0.381 08Nt+ 4.981 5D−1.046 5Db−5.647 2)；

h3= logsig (1.635C−2.413 6Nt−0.163 18D−4.040 7Db−2.106 9)；

h4= logsig (0.940 89C+ 2.839 6Nt−6.912 5D−1.823 8Db−1.757 9)；

h5= logsig (1.224C−2.715 7Nt−2.839 4D−4.562 5Db−2.169)；

h6= logsig (1.193 2C+ 3.811 7Nt−7.989 1D−0.911 14Db−0.853 18)；

h7= logsig (1.955 4C−2.838 1Nt+ 2.935 2D−1.89Db+ 3.127 6)；

h8= logsig (−3.880 3C+ 0.570 5Nt−2.167 3D−2.634 9Db−3.617 8)；

h9= logsig (−3.781 5C+ 2.025 1Nt+ 2.536 2D+0.408 18Db−4.022 4)；

3 讨论

灌木生物量模型应选择所研究灌木的易测因子作为模型构建的自变量，往往不同形态特征的灌木，宜采用不同的变量构建生物量模型，所以应根据所研究灌木的形态特征来选取最优灌木易测因子作为模型构建的自变量[11]。由于BP 神经网络模型的自身特性，增加输入变量的数量，可以使得模型的泛化能力提高，增加模型精度[22-23]。对于本研究来讲，模型输入变量尽可能的囊括沙柳所有可以测量的形态指标，并以沙柳各因子与沙柳生物量的相关关系为基础进行筛选，在最优模型中输入因子包括冠幅C、基部分支数Nt、地径D、枝条粗度Db共4 种。输入变量中输入因子数量的增加可以使得模型精度不断上升。

在风沙区，由于风大沙多，灌木基部容易产生沙埋的现象，使得基径的测量比较困难，考虑到模型在日常生产中的易用性和实用性，在构建生物量模型时要结合实际工作考量不同的建模因子[24]。本研究中地径与生物量相关性为0.631。如果使用相关性不如地径但更为简单易测的两个或多个因子进行建模，是否在模型性能上可以替代相对不易测的地径参与建模的模型呢？在未来的沙区灌木生物量模型研究中，应将实际工作中灌木因子的测量难易程度加入建模输入因子筛选的条件中，对比低相关但相对易测因子与高相关性但测量困难的因子对生物量估算模型性能的影响。

本研究选择6 种BP 神经网络的输入因子均为沙柳的测树因子，并未包括环境因子，将林分因子和气候因子等变量共同参与生物量预测模型的拟合，对于模型的性能有较大的提高[17]。坡向、坡位、立地条件、海拔和林分密度等环境因素对林木的生长发育也有很大的影响，将以上因子加入到模型的拟合会有效提高模型精度[25]。本研究中尚未将丘间低地未沙埋、丘间低地沙埋、迎风坡风蚀3 种立地条件考虑到模型的建模当中，接下来的研究中要探究不同立地条件对的沙柳BP 神经网络生物量预测模型的影响。

4 结论

本研究以库布其沙漠沙柳为研究对象，为其分别建立传统沙柳生物量模型和基于BP 神经网络的沙柳生物量模型，探究不同建模因子下的沙柳生物量估算模型变化。根据沙柳生长因子相关性大小，输入变量所包含的输入因子由1 种逐渐增加至最大6 种，拟合发现，随着输入变量中输入因子的数量不断增加，输入变量达到6 种时R2（0.91）、RMSE（1.24）、MAE（0.78）所表现出的模型性能最好，输入变量每增加1 种后，模型性能提升幅度不尽相同，当输入因子数量为5 时，模型精度相比输入因子数量为4 时提升幅度较小，考虑到在模型使用时要同时兼顾其使用精度和野外实地调查时的工作强度和调查量大小，故选择输入变量中，输入因子为4 种时为最佳，则其输入层最优输入因子数为4 种。在确定模型结构输入为4，输出为1 的前提下，对模型各隐层数不断训练，当隐层数为9 时，模型性能表现为最优，则基于BP 神经网络的沙柳生物量估算模型最优结构[输入层节点数(Nin)∶隐层节点数(Nh)∶输出层节点数(Nout)]=4∶9∶1。