移频转发密集假目标干扰效应分析与应用研究
2022-05-24王志凇化斌斌任新涛
王志凇,化斌斌,孙 彬,任新涛
(中国人民解放军32200 部队,辽宁 锦州 121007)
0 引言
移频转发干扰利用线性调频脉冲压缩雷达固有的距离-多普勒频移间存在强耦合的弱点,通过对截获的雷达发射信号调制一个附加频率后转发给原雷达,达到距离假目标干扰效果,是对抗线性调频脉冲压缩雷达的行之有效的手段。
线性调频脉冲信号的斜刀刃形状模糊函数特性,导致其在距离-多普勒频移间存在强耦合,进而引起距离随多普勒变化的视在漂移而产生测距误差。由此出发,文献[2-4]分别论述了单点移频、阶梯波移频和随机噪声移频干扰对线性调频雷达的干扰效果;文献[5]进一步对比分析了移频干扰对线性调频和相位编码信号的干扰效果。上述文献大多采用定性、半定量方式分析移频干扰的影响效果,并借助仿真手段进行验证,对通过移频转发产生密集多假目标的机理分析不够深入,同时未定量表征干扰的影响效应,移频量与最终引起距离误差之间的解析表达式尚未推导得出。这对于移频干扰的工程应用多有不利。
显然,对于移频干扰要注意在干扰过程中隐蔽移频量这一典型特征。例如,为了防止雷达测量出移频量,干扰时要求移频量不能过大。但对于自卫式干扰,如果不足够大,则假目标有可能变成为信标。比较实用的方法是对移频量施加特定的变化规律,使雷达无法有效地利用该特征来计算真假目标的距离差。改变移频量,可以采用阶梯波移频、线性函数移频、分段线性函数移频等典型方法,它们会产生不同的假目标干扰效果。
基于此,本文从深入分析移频转发干扰对线性调频脉冲压缩雷达的作用机理入手,建立起失配干扰峰值、假目标时延、假目标主峰宽度等干扰效应与干扰参数的解析表达式,然后从工程应用角度出发,设计出阶梯波移频、线性函数移频、分段线性函数移频三种典型移频方法,并通过仿真实验逐一进行验证和对比分析,从而完成移频转发密集多假目标干扰影响效应的定量表征。
1 移频转发干扰作用机理
线性调频信号的复数表达式为:
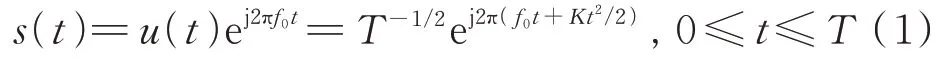
式中,()为信号复包络,为脉冲宽度,=为调频斜率,为调制带宽。
分析线性调频信号的模糊函数可以得到如下结论:在进行距离-多普勒二维联合估计时,线性调频脉冲信号的时延与频移之间存在着强耦合,如果对截获到的雷达信号移频后再转发给原雷达,就能够实现距离欺骗的目的。干扰系统对截获的雷达信号移频后转发,干扰信号进入雷达接收机,在匹配滤波器的输入端表现为频率发生了的频移,因此移频干扰信号可以表示为:

式中,为附加频移,经过匹配滤波后的输出为:
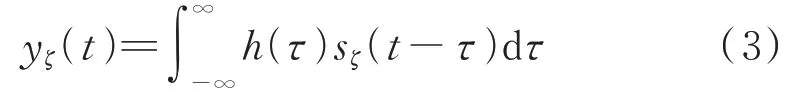
省略对式(3)的详细推导,直接给出匹配滤波输出的解析表达式(即式(4)),结果表明:移频干扰经雷达匹配滤波后的输出信号是一个单频振荡信号,其中心频率为+2+/2,振荡包络为:
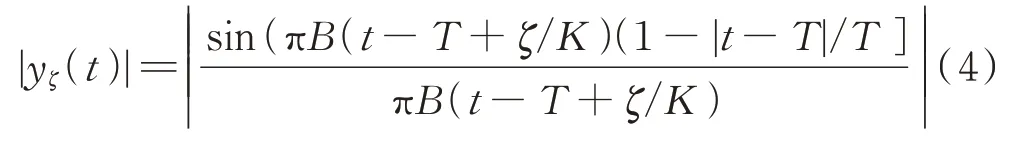
振荡包络的波形如图1 所示。从图中可看出,当频移=0 时,脉压输出在输入脉冲结束时刻出现主峰,主峰宽度为[-1,1],输出信号包络按照sinc()函数规律衰减。当频移非零时,脉压输出主峰将偏移到=-/处,> 0 则主峰导前,反之则主峰延后。从原理上分析,是因为延迟-和频移间存在耦合作用,所以附加有频移的回波经匹配滤波处理后会引起失配,输出主峰宽度展宽、幅度按照三角包络下降,相应的干扰功率会出现失配损失,频移越大,失配越严重。
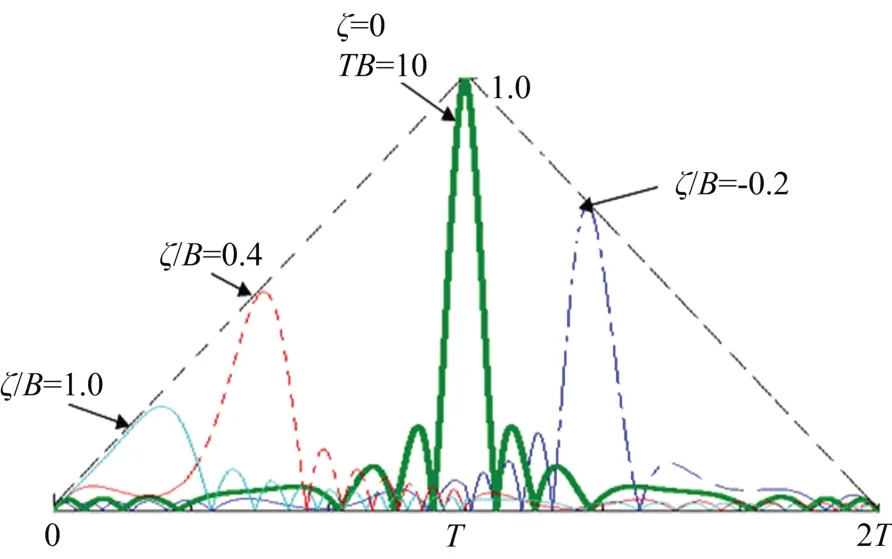
图1 移频干扰匹配滤波后输出包络
下面从匹配滤波器和干扰信号的频谱入手进行进一步对比,如图2 所示。
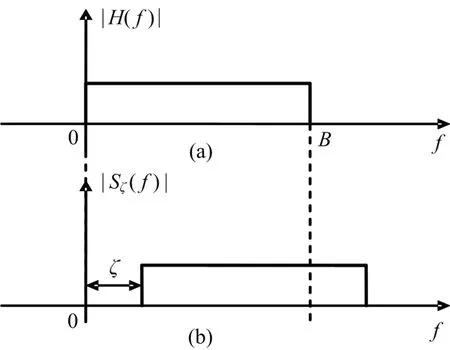
图2 匹配滤波器和移频干扰信号的频谱
当>>1 时,匹配滤波器的幅度谱在频率范围[0,]内近似为一矩形,如图2(a)所示。对于移频信号,干扰信号的幅度谱在[,+]内近似也为一矩形,如图2(b)所示。只有二者重合的部分才能够产生有效干扰输出,当||越大,它们重合度越小,即假目标的能量越小,当||≥时将不再产生假目标。综合可知,如果雷达接收相同功率的干扰和目标,则失配干扰峰值y与匹配信号峰值的关系式为:
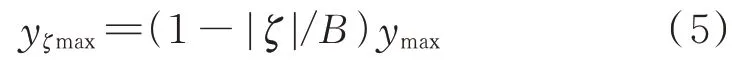
从式(4)可知,假目标相对于真目标发生的时延为:

可见,当||越大时时延越大。同时根据辛格函数性质得到假目标主峰宽度为:

干扰信号中的频移一方面使雷达受到距离欺骗(表现为使信号包络发生时移,假目标回波相对地发生前移或后移,从而产生距离欺骗干扰效果),另一方面它还会使雷达匹配滤波后的单频振荡的中心频率发生改变(相对于真目标回波经匹配滤波后的振荡中心频率),改变量为/2,并且只与频移量有关,这便是移频干扰的典型特征。
2 阶梯波移频干扰影响效应
阶梯波移频干扰的思想是将整个脉冲宽度均匀地等分为段,每个子段长度Δ=。设干扰机起始调制频率为,频率间隔为Δ,则在每个子段内附 加 的 频 移 依 次 为 ζ=+Δ,其 中=0,1,…,-1。其中的每一段干扰信号,对于匹配滤波器而言它都是一个窄的失配线性调频脉冲,故每段干扰信号都可能产生一个假目标,但因为只有在[,]范围内的干扰频谱分量才能在匹配滤波器输出端产生响应,而每个假目标频率宽度为Δ+Δ,所以在没有时域混叠的情况下,产生的假目标个数为:

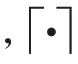
假目标相对于真目标的时延由式(6)确定,即第个假目标相对于真实目标的时延为:
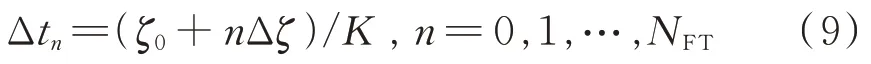
经过分析可知,距离目标最近的-1 个假目标的峰值为信号峰值的1,最远的一个假目标幅度将小于它的1。为了避免多个假目标在时域上产生混叠,调制频率间隔Δ引起的前移距离必须大于干扰输出的3 dB 宽度。
3 线性函数移频干扰影响效应
线性函数移频的思想是干扰机调制频率按时间线性变化。如果在整个脉冲宽度内,干扰机调制的初始频率为,调频斜率为K,则干扰信号本身的调制带宽为B=KT。根据移频转发干扰作用机理分析,这种干扰经匹配滤波器的输出与真实目标回波经过匹配滤波器的输出相比不再是一个峰值,而是被展宽了,形成覆盖前移干扰。覆盖前移干扰近端与真目标的延时为:
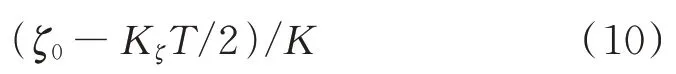
相应地覆盖宽度为:
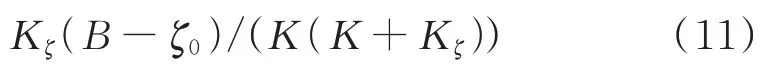
由式(10)和式(11),能够比较容易地得到覆盖前移干扰远端与真目标的延时。接下来推导覆盖前移干扰峰值与匹配信号输出峰值的定量关系。用复数包络来进行分析,干扰信号包络为:
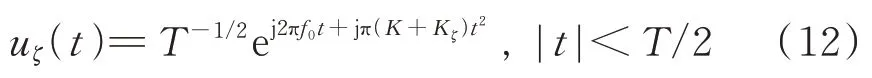
对式(12)的信号进行匹配滤波,对匹配滤波输出的频谱进行Fourier 反变换,省略具体的推导过程,最终得到输出信号为:

在式(13)中,当-满足式(10)和(11)定义的范围时,,近似为常数,在其他区间近似为0,则干扰峰值为:

从式(14)可以看出,覆盖前移干扰的峰值幅度与干扰机调制的初始频率、信号脉冲宽度等无显著关联,主要取决于调频斜率。因此,覆盖前移干扰峰值与匹配信号输出峰值的定量关系为:
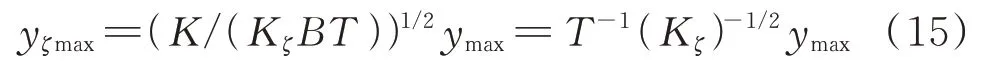
4 分段线性函数移频干扰影响效应
类似于阶梯波移频法的思想,分段线性函数移频也是把整个脉冲宽度均匀地等分为段,每个子段长度为,初始调制频率为,间隔为Δ,且在每个时间间隔内频率按线性函数变化,其移频规律示意图如图3 所示。图中,每个时间间隔内的频率是线性增加的。
按照图3 所示的规律,把整个100 μs 的脉冲均匀分为4 段,干扰机起始调制频率为1.5 MHz,步进间隔为0.4 MHz,每个子段内的调制斜率可以进行设置。按照前2 节的分析,通过改变初始点频率或斜率以及各段的间隔频率,将会得到不同位置不同形状不同数目的覆盖干扰。
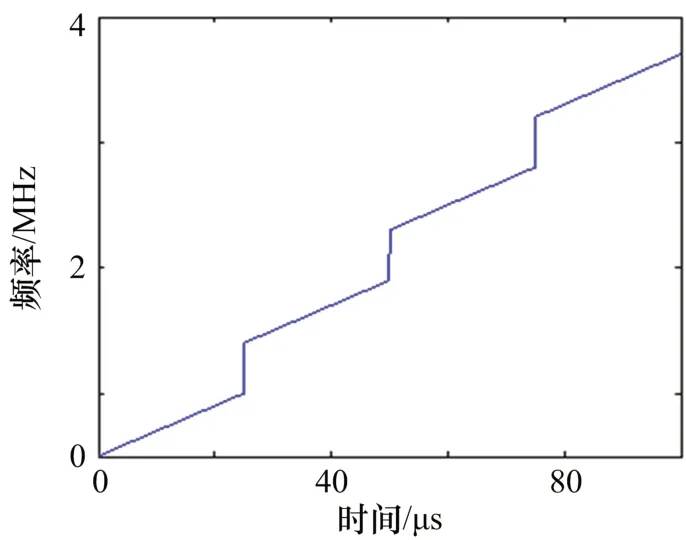
图3 等间隔分段线性移频
5 仿真实验
本节设置典型参数,分别完成理想工作、阶梯波移频干扰、线性函数移频干扰、分段线性函数移频干扰四个场景下的匹配滤波与包络检波,从而完成移频转发干扰效果定量分析。
5.1 理想场景
假设雷达脉冲宽度为100 μs,调制带宽10 MHz,仿真采样率为20 MHz,采用正交双通道采样。目标真实距离为12.5 km。在接收机中设置接收窗口,起始距离为5 km,结束距离为20 km。采用归一化功率值,信噪比设定为10 dB。
依据目标所处真实距离产生对应的时间延迟,生成回波复信号序列,并按照设定的信噪比叠加接收机热噪声。接下来采用频域处理的方法来实现匹配滤波(脉冲压缩)处理,具体步骤为:首先求取发射信号本地样本的频谱,然后获取回波信号序列的频谱,二者相乘后进行频域相乘,进行Fourier 反变换和循环移位,再按照补零FFT 点数进行序列截断处理,便得到了匹配滤波后的结果,最后进行包络检波操作,并进一步将包络进行归一化操作。
在理想工作场景下,得到如图4 所示仿真结果。由于不存在人为频移干扰,不会因距离-多普勒频移耦合而导致主峰位置偏离,所以经过脉压、包络检波等操作后,主峰位于12.5 km 处,与目标的真实距离相同。根据设置的参数,脉压比为1 000,因而窄脉冲宽度约为0.1 μs,此时对应的距离分辨率约为15 m。
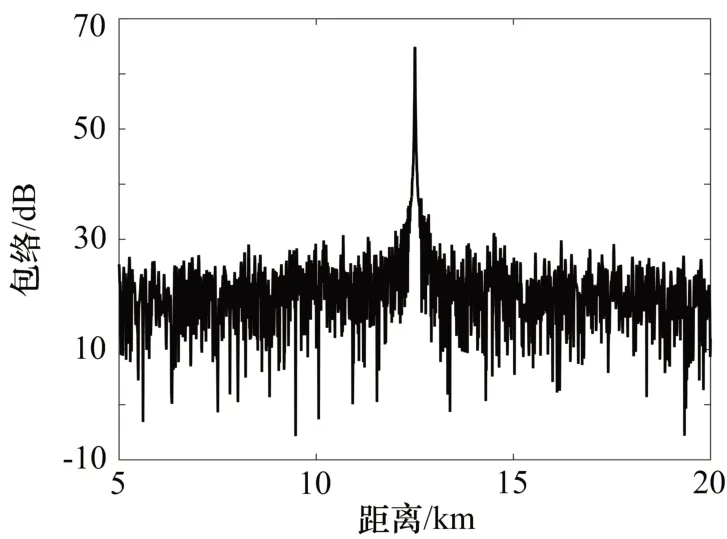
图4 理想条件仿真结果
5.2 阶梯波移频干扰场景
在理想工作场景基础上,考虑阶梯波移频干扰影响效果。首先假设将100 μs 的脉冲等分为5 份,每个子段的脉宽为20 μs,暂不考虑干扰机起始调制频率,调制频率间隔设置为0.2 MHz(正向调制)。当干扰机截获雷达辐射脉冲信号后,首先将其存储在DRFM中,干扰启动后由DRFM 复制出原雷达信号,再在上变频时通过给上变频本振调制一个额外频移,从而产生移频干扰信号。
综合考虑接收窗口及干扰机对雷达信号的截获时序,得到如图5 所示的移频变化,从中可直观地看到分为5 个子段进行阶梯移频。上述阶梯波移频干扰信号通过脉冲压缩后,由于每一段干扰信号对于匹配滤波器而言它都是一个窄的失配线性调频脉冲,故可能产生一个假目标。按照设置参数,每个假目标的频率宽度为Δ+Δ,经计算为2.2 MHz,按照式(8)最终产生的假目标个数为5 个,这与图6(a)所示的仿真结果一致。
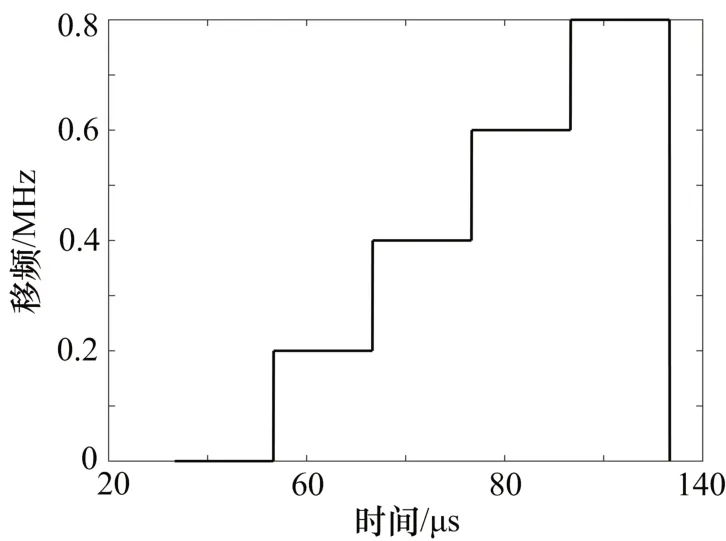
图5 阶梯移频
同时,因为调制频率间隔引起的前移距离大于干扰输出的3 dB 宽度,所以可以确保多个假目标不会重叠在一起,与第2 节中的理论分析一致。另外,因为每一段干扰信号都视为一个窄的失配的线性调频脉冲,所以它产生的干扰主峰应该比单个假目标展宽得更多,图6(a)仿真结果证实了这一点。采用负向调制时,根据前述理论分析,此时附加的移频量为负值,主峰延后,将相应地产生延后的多个假目标,如图6(b)所示。
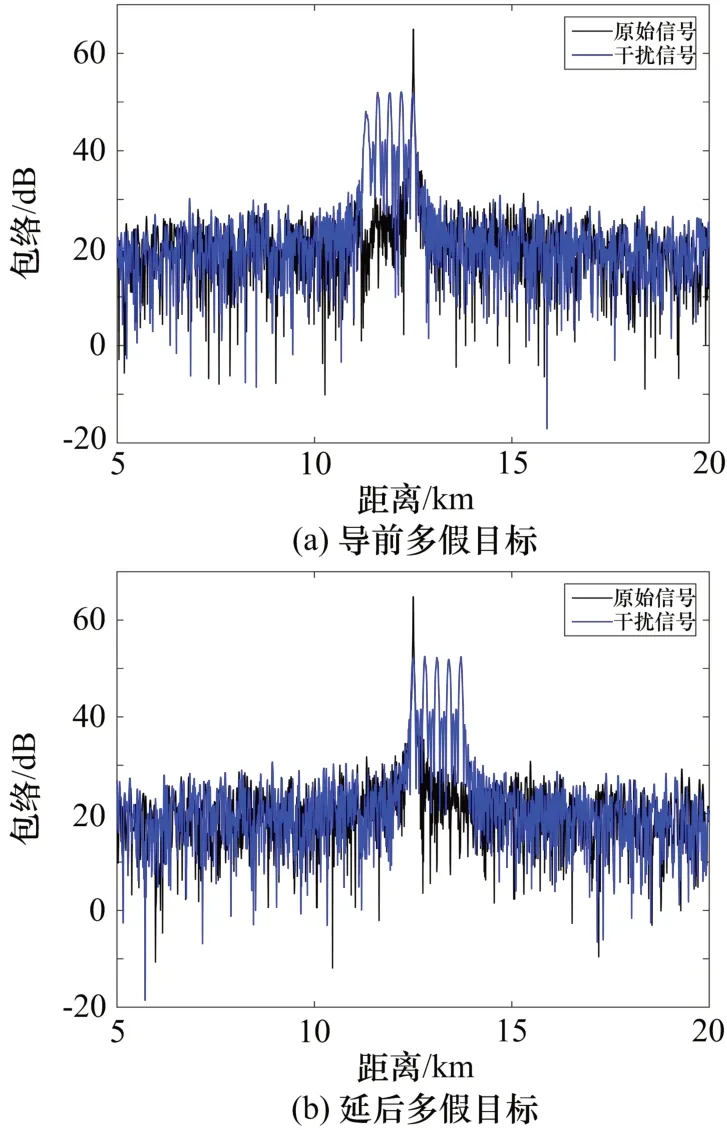
图6 阶梯移频干扰仿真结果
通过观察图5 所示的阶梯波移频法的移频规律发现,它的移频量实际上是一个线性函数的离散化结果。正是由于其移频量的离散变化,最终导致出现了多个假目标。为了进一步验证调制频率间隔对于干扰结果的影响,将频率间隔设置为1.0 MHz,其它参数不变。经过匹配滤波后,得到如图7 所示的结果。从图中可看出,因为只有在[,]频率范围内的干扰才能够有效地通过匹配滤波器,所以产生的假目标数量减少为4 个,干扰主峰也展宽得更多。
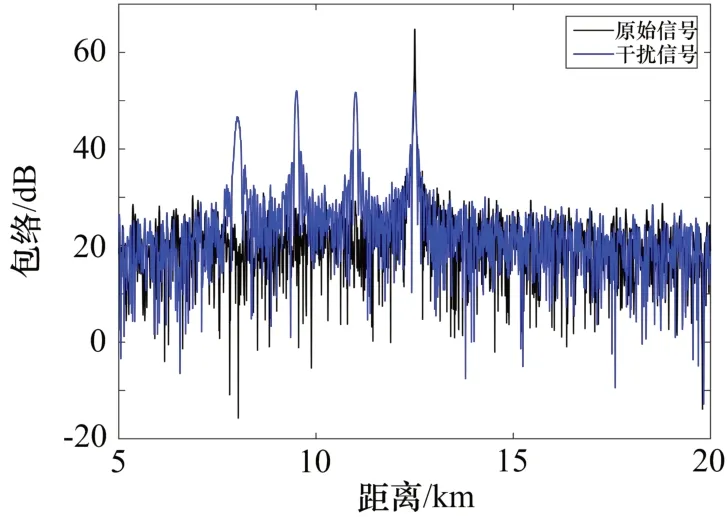
图7 增加频率间隔后阶梯移频干扰仿真结果
5.3 线性函数移频干扰场景
本节考虑线性函数移频干扰效果,假定干扰机起始调制频率为1.0 MHz,线性函数移频调频斜率为20 kHz/μs,其余参数保持不变。通过仿真,得到如图8 所示的覆盖干扰。按照式(10)来计算覆盖前移干扰近端与真目标的延时,在当前参数设置下该延时恰好为0,这与图8 所示结果一致。按照式(11)来计算覆盖宽度,经过计算为15 μs,对应距离范围为2.25 km,同样与仿真结果一致。
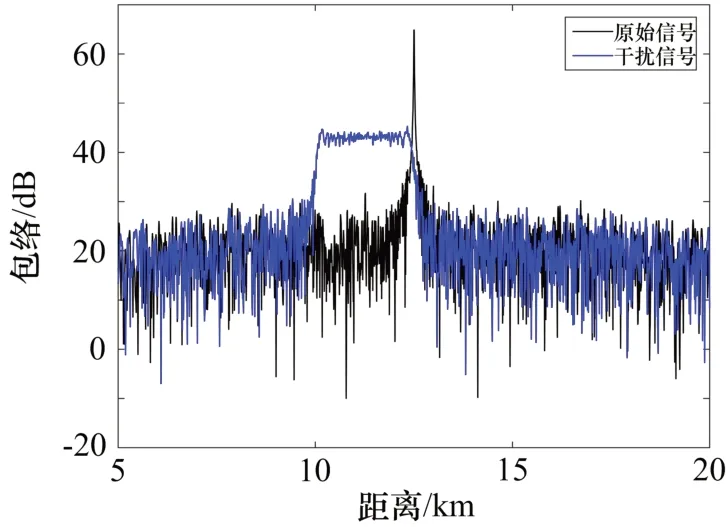
图8 线性函数移频干扰仿真结果
干扰机采用不同线性函数,例如改变初始点频率或斜率,将会得到不同位置不同形状的覆盖干扰。干扰机起始调制频率值保持不变,适当减小调频斜率至10 kHz/μs,其余参数保持不变。通过仿真,得到如图9 所示的覆盖干扰。
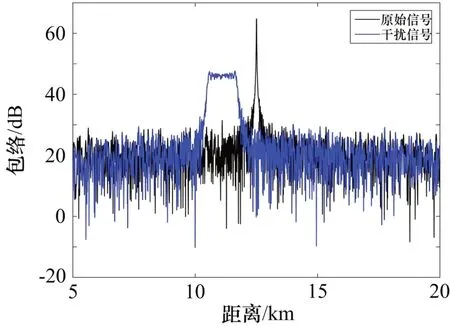
图9 减小调频斜率后线性函数移频干扰仿真结果
按照同样的方法,计算得到此时覆盖前移干扰近端与真目标的延时为50 μs,覆盖宽度对应的距离范围为1.227 km,均与图9 仿真结果一致。
5.4 分段线性函数移频干扰场景
按照图3 所示规律,把整个100 μs 的脉冲均匀分为4 段,干扰机起始调制频率为1.5 MHz,步进间隔为0.4 MHz,调频斜率为20 kHz/μs,其余参数保持不变。
通过仿真,得到如图10 所示的多个覆盖干扰。根据理论计算,覆盖干扰假目标数目为3 个,与实际仿真相符。同样地,通过改变初始点频率或斜率以及各段的间隔频率,还会得到不同位置不同形状不同数目的覆盖干扰。将干扰机起始调制频率为-1.5 MHz,其余参数均保持不变,产生的覆盖干扰效果将随之改变。

图10 分段线性函数移频干扰
如果组合其中(可包括前面分析的单个假目标)的2 种或更多种方法,还将会产生更复杂的干扰效果,文中不再赘述。
6 结束语
本文在深入分析移频转发干扰对线性调频脉冲压缩雷达的作用机理的基础上,建立起干扰效果与干扰参数的解析表达式,然后从工程应用角度出发,设计出阶梯波移频、线性函数移频、分段线性函数移频三种典型移频方法,并通过仿真实验逐一进行验证和对比分析,从而完成移频转发密集多假目标干扰影响效应的定量表征,主要结论如下:
1)移频转发干扰一方面使雷达受到距离欺骗,另一方面使雷达匹配滤波后的单频振荡的中心频率发生改变,且仅与频移量有关。
2)采用阶梯波移频方法,移频干扰可产生多个距离假目标欺骗干扰效果,且只有在[,]频率范围内的干扰才能产生假目标。
3)采用线性移频方法,移频干扰可产生单个遮盖干扰效果,覆盖前移干扰近端延时、覆盖宽度、干扰峰值幅度可精确推导得出。
4)采用分段线性移频方法,移频干扰可产生多个遮盖干扰效果。通过改变初始点频率或斜率以及各段的间隔频率,将会得到不同位置不同形状不同数目的覆盖干扰。
5)组合阶梯波移频方法、线性移频方法、分段线性移频方法中的2 种或更多种方法,还会产生更复杂的干扰效果。
