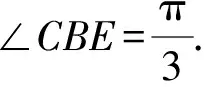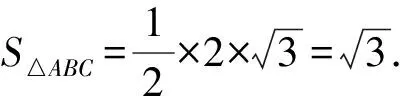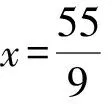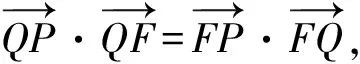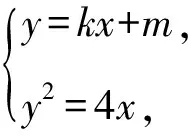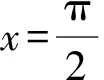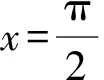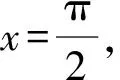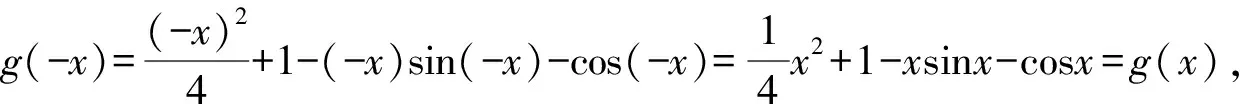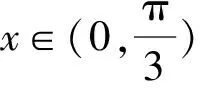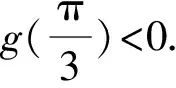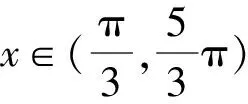2022届高考模拟考试文科数学试题(本试卷适合老高考地区文科考生使用)

李昌成

(新疆乌鲁木齐市第八中学 830002)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,时量120分钟．满分150分．

第Ⅰ卷

一、选择题(本大题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的)

1.已知集合M={x|-34}，则M∪N=( ).

A.{x|x<-5或x>-3}

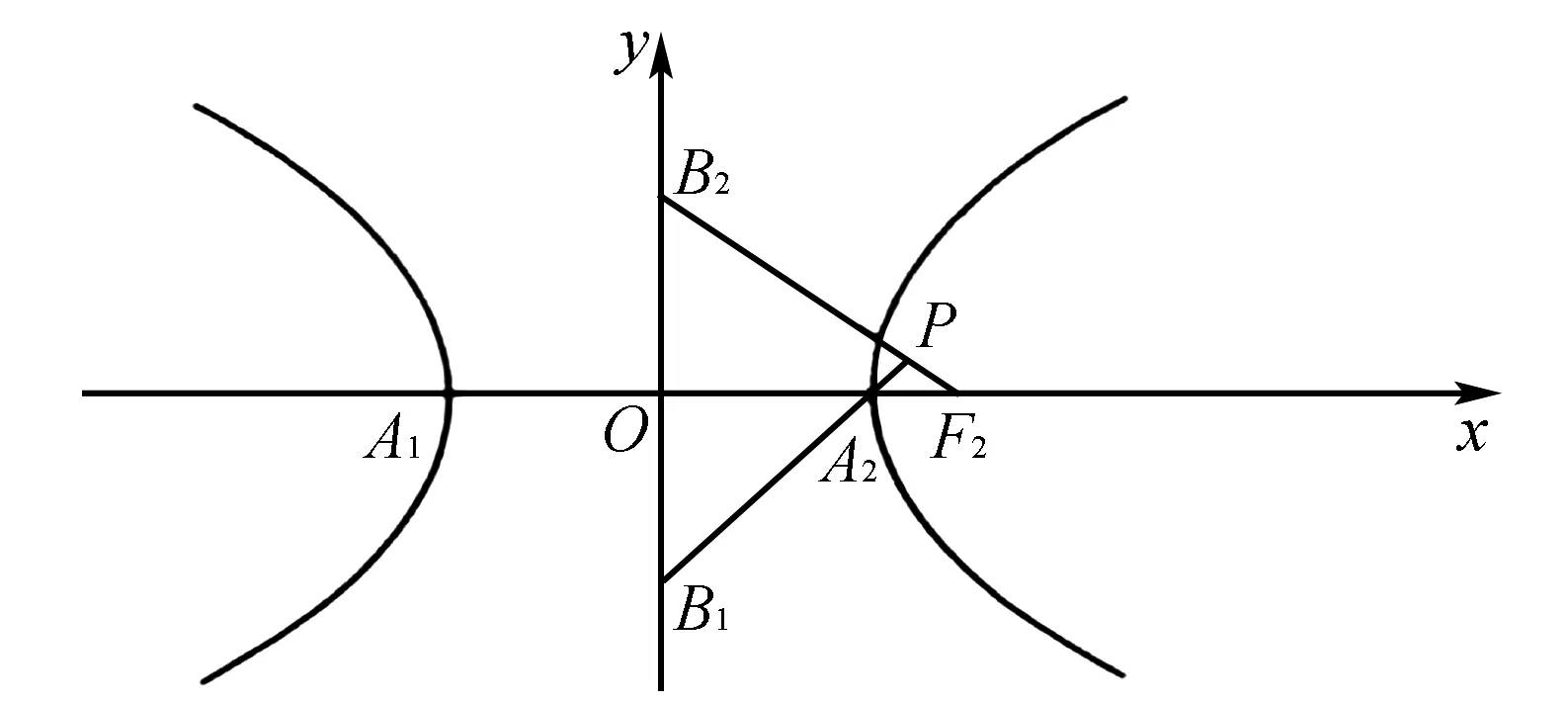
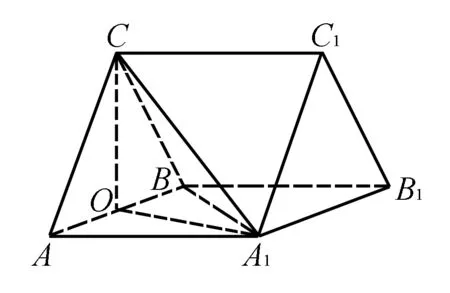
B. {x|-5

C. {x|-3

D. {x|x<-3或x>5}

2.已知a=(3,-1),b=(-1,2),c=2a+b，则c=( ).

A.(6,-2) B.(5,0) C. (-5,0) D. (0,5)

A.1+i B.1-i C. -1+i D. -1-i

4.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想的内容是：每个大于2的偶数都可以表示为两个素数的和，例如：10=5+5=3+7(其中3+7与7+3算同一种方法)，在大于4且不超过16的偶数中，随机选取两个不同的偶数，则两个偶数都可以有两种方法表示为两个素数的和的概率为( ).

5.一个总体中有600个个体，随机编号为001，002，…，600，利用系统抽样方法抽取容量为24的一个样本，总体分组后在第一组随机抽得的编号为006，则在编号为051～125之间抽得的编号为( ).

A.056，080，104 B.054，078，102

C. 054，079，104 D. 056，081，106

6.我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯( ).

A.1盏 B.3盏 C. 5盏 D. 9盏

图1

A.6 B.7 C. 8 D. 9

11.图2网格纸中小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为( ).

图2

第Ⅱ卷(非选择题，共90分)

二、填空题(本大题共4小题，每小题5分)

13.等比数列{an}中，4a1,2a2,a3成等差数列，若a1=1，则公比q=____．

16.如图3，双曲线的中心在坐标原点，焦点在x轴上，A1，A2为双曲线的顶点，B1，B2为双曲线虚轴的端点，F2为双曲线的右焦点，延长B1A2与F2B2交于点P，若∠B1PB2为锐角，则该双曲线的离心率的取值范围是____．

图3

三、解答题(解答应写出文字说明、证明过程或演算步骤.)

(1)求角C．

(2)若BC=4，△ABC的中线CD=2，求△ABC的面积．

18.(本小题满分12分)如图4，在三棱柱ABC-A1B1C1中，O为AB的中点，CA=CB，AB=AA1，∠BAA1=60°．

图4

(1)证明：AB⊥平面A1OC;

(2)若AB=CB=2，OA1⊥OC，求三棱锥A1-ABC的体积．

19.(本小题满分12分)十九大提出：坚决打赢脱贫攻坚战，做到精准扶贫，某省某科研机构帮助某贫困县的农村村民真正脱贫，坚持扶贫同扶智相结合，积极引导该县农民种植一种名贵中药材，从而大大提升了该村村民的经济收入．2019年年底，该机构从该县种植了这种名贵药材的农户中随机抽取了n户，统计了他们2019年因种植中药材所获纯利润(单位：万元)的情况(假定农户因种植中药材这一项一年最多增加11万元)，并分成以下几组：[1,3)，[3,5)，[5,7)，[7,9)，[9,11]，统计结果见下表所示，已知样本中数据落在[9,11]这一组的频率为0.1.

纯利润1,3[)3,5[)5,7[)7,9[)9,11[]频数2030a4020

(1)求n和表中a的值；

(2)试估计该贫困县农户因种植中药材所获纯利润的平均值和中位数(同一组中的数据用该组区间中点值为代表)．

(1)求动点P的轨迹C的方程．

(2)设动直线y=kx+m与曲线C相切于点M，且与直线x=-1相交于点N，试问：在x轴上是否存在一个定点E，使得以MN为直径的圆恒过此定点?若存在，求出定点E的坐标;若不存在，请说明理由．

(1)求f(x)在区间(0,2π)上的极值点；

(2)证明：g(x)恰有3个零点．

请考生在第22，23题中任选一题做答，如果多做，则按所做的第一题记分，做答时请写清题号.

(1)求曲线C2的直角坐标方程；

23.(本小题满分10分)已知函数f(x)=-x2+ax+4，g(x)=|x+1|+|x-1|．

(1)当a=1时，求不等式f(x)≥g(x)的解集；

(2)若不等式f(x)≥g(x)的解集包含[-1,1]，求a的取值范围．

参考答案

一、选择题

1.A 2.B 3.D 4.D 5.D 6.B 7.C 8.A 9.D 10.B 11.C 12.A

二、填空题

三、解答题

17.(1)由正弦定理及已知条件，得

两边同乘ab，得a2+b2-c2=-ab．

(2)方法1设AC=x，AD=BD=y，

由余弦定理，得

即x2+16-4y2=-4x.

①

根据余弦定理，得

因为∠ADC与∠BDC互补，

所以cos∠ADC+cos∠BDC=0.

即2y2-x2-8=0.

②

方法2延长CD至点E，使DC=DE，连接AE，BE，则所得四边形ACBE是平行四边形.

又因为CE=2CD=4，BC=4，

所以BE=4，AC=4．

18.(1)因为CA=CB，O为AB中点，所以OC⊥AB.

因为AB=AA1，∠BAA1=60°，

所以△AA1B为等边三角形，即OA1⊥AB.

又OC∩OA1=O，OC，OA1⊂平面A1OC，

所以AB⊥平面A1OC．

(2)因为AB=CB=2，

所以△ABC为边长是2的等边三角形，

因为OA1⊥AB，OA1⊥OC，AB∩OC=O，AB，OC⊂平面ABC，所以OA1⊥平面ABC.

即OA1是三棱锥A1-ABC的高.

所以a=200-20-30-40-20=90．

(2)计算可得样本中的数据落在每个区间的频率分别为0.1，0.15，0.45，0.2，0.1，所以农户种植中药材所获纯利润的平均值为2×0.1+4×0.15+6×0.45+8×0.2+10×0.1=6.1(万元)．

因为前2组的频率为0.25<0.5，前3组的频率为0.7>0.5，所以样本的中位数在第三组，设样本的中位数为x(万元)，

20.(1)设点P(x,y)，则Q(-1,y).

得(x+1,0)·(2,-y)=(x-1,y)·(-2,y).

化简得动点P的轨迹C的方程为y2=4x．

k2x2+(2km-4)x+m2=0.

由Δ=0，得km=1.

假设存在点E(x0,0)满足ME⊥NE，则

①

当x0=1时，①式恒成立．

所以存在一个定点E(1,0)，使得以MN为直径的圆恒过此定点．

21.(1)f′(x)=xcosx(x∈(0,2π))，

因为g(0)=0，所以x=0是g(x)的一个零点.

即要确定g(x)在R上的零点个数，只需确定x>0时，g(x)的零点个数即可．

当x>0时，

又因为t(x)开口方向向上，对称轴为x=2，

所以g(x)在区间(0,+∞)内有一个零点，

由于g(x)是偶函数，所以g(x)在区间(-∞,0)内有一个零点，而g(0)=0.

综上，g(x)有且仅有三个零点．

(2)曲线C1的极坐标方程为ρ=4cosθ，曲线C2的极坐标方程为ρ=4sinθ．

23.(1)当a=1时，f(x)=-x2+x+4，

当x>1时，令-x2+x+4≥2x，

当-1≤x≤1时，令-x2+x+4≥2，

解得-1≤x≤1，则f(x)≥g(x)的解集为[-1,1].

当x<-1时，令-x2+x+4≥-2x，此时无解，则f(x)≥g(x)的解集为Ø．

(2)依题意-x2+ax+4≥2在[-1,1]恒成立.

即x2-ax-2≤0在[-1,1]上恒成立.

解得-1≤a≤1，故a的取值范围是[-1,1]．