2021年全国甲卷理第5题的多视角解答赏析

李 勇

(贵州省贵阳市息烽县第一中学 551100)

1 试题呈现

题目已知F1，F2是双曲线C的两个焦点，P为C上一点，且∠F1PF2=60°，|PF1|=3|PF2|，则C的离心率为( ).

2 试题解答

解析不妨设C是中心在原点，焦点在x轴上的双曲线，如图1所示.

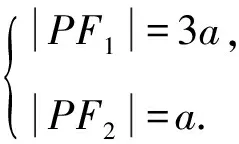
视角1特值法(条件附值推结果).

令a=1，则|PF2|=1，|PF1|=3.

图1

在△F1PF2中，由余弦定理，得

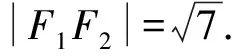
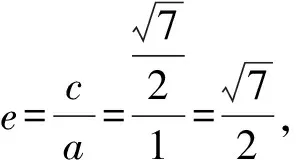
点评对部分条件附值，有利于降低试题在运算过程中的难度，提高解题效率.

视角2 特值法(结果附值，验证是否满足条件).

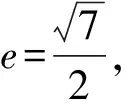
在△F1PF2中，由余弦定理,得

点评对目标附值，通过逆向思维，验证是否满足条件，排除选项，这是在解答选择题时常用的一种方法，它也有利于降低试题在运算过程中的难度，提高解题效率.

视角3 排除法(点与圆的位置关系).

因为O为F1F2的中点，

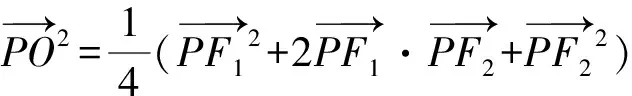
因为∠F1PF2=60°，

所以点P在以F1F2为直径的圆的外部.

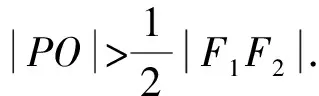
所以排除B，C，D，故选A.

视角4排除法(大角对大边，大边对大角).

由|PF1|=3a，|PF2|=a，|F1F2|=2c，

得|PF2|最小.

若|F1F2|最大，由∠F1PF2=60°，

则△PF1F2的内角和小于180°，这与三角形的内角和定理矛盾.

故|PF1|最大，所以∠PF2F1>∠F1PF2=60°.

所以排除B，C，D，故选A.

点评利用大角对大边，大边对大角，得出a，c的关系，从而得出离心率的范围，排除其他选项.

视角5面积法(已知三角形两边和它们的夹角的面积公式和海伦公式).

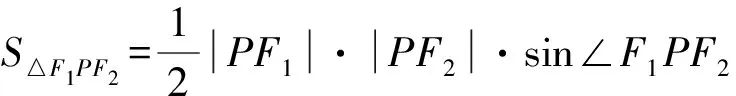
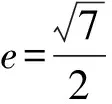
由|PF1|=3a，|PF2|=a，|F1F2|=2c，

得|PF2|最小.

若|F1F2|最大，由∠F1PF2=60°，则△PF1F2的内角和小于180°，这与三角形的内角和定理矛盾.

故|PF1|最大，所以∠PF2F1>∠F1PF2=60°.

所以3a>2c.

点评利用等面积法计算出离心率的值，再利用大角对大边，大边对大角排除干扰答案.

视角6面积法(双曲线焦点三角形的面积公式和海伦公式).

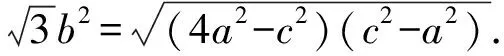
点评利用等面积法计算出a，b，c的关系，再配合a2+b2=c2，解出a，b关系，最后利用离心率公式求解.

视角7面积法(已知三角形两边和它们的夹角的面积公式和双曲线焦点三角形的面积公式).

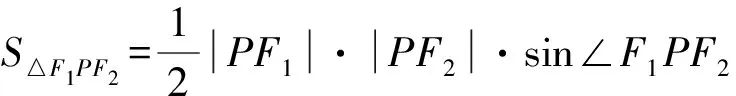
点评利用等面积法计算出a，b的关系，然后利用离心率公式求解.

视角8面积法(双曲线焦点三角形的面积公式和双曲线的焦半径公式).

设点P的坐标为(x0，y0),

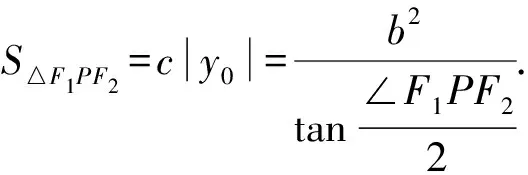
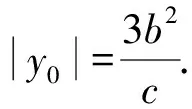
由双曲线的右焦半径公式,得

|PF2|=ex0-a.

则4a2-3b2=c2.

点评利用等面积法计算出点P的纵坐标，利用焦半径公式计算出点P的横坐标，然后将其代入双曲线的方程中，解出a，b，c的关系，再配合a2+b2=c2，解出a，b关系，最后利用离心率公式求解.

视角9余弦定理.

在△F1PF2中，由余弦定理，得

|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos∠F1PF2.

点评直接利用余弦定理解出a，c的关系，再后利用离心率公式求解.

视角10正弦定理.

因为|PF1|=3|PF2|，由正弦定理,得

sin∠PF2F1=3sin∠PF1F2.

又因为∠F1PF2=60°，

所以∠PF2F1+∠PF1F2=120°.

所以3sin∠PF1F2=sin(120°-∠PF1F2)

=sin120°·cos∠PF1F2-cos120°·sin∠PF1F2

又因为sin2∠PF1F2+cos2∠PF1F2=1，

在ΔF1PF2中，由正弦定理,得

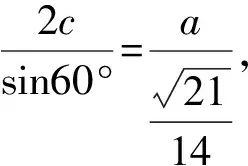
点评多次利用正弦定理解出a，c的关系，再利用离心率公式求解.

视角11正弦定理→双曲线的离心率公式.

因为|PF1|=3|PF2|，由正弦定理,得

sin∠PF2F1=3sin∠PF1F2.

又因为∠F1PF2=60°，

所以∠PF2F1+∠PF1F2=120°.

所以3sin∠PF1F2=sin(120°-∠PF1F2).

所以3sin∠PF1F2=sin120°·cos∠PF1F2-cos120°·sin∠PF1F2.

又因为sin2∠PF1F2+cos2∠PF1F2=1，

由双曲线的离心率公式

点评利用正弦定理解出三角形的三个内角的正弦值，再利用离心率公式求解.

视角12正弦定理→双曲线的焦半径公式.

因为|PF1|=3|PF2|，由正弦定理,得

sin∠PF2F1=3sin∠PF1F2.

又因为∠F1PF2=60°，

所以∠PF2F1+∠PF1F2=120°.

所以3sin∠PF1F2=sin(120°-∠PF1F2).

所以3sin∠PF1F2=sin120°·cos∠PF1F2-cos120°·sin∠PF1F2.

又因为sin2∠PF1F2+cos2∠PF1F2=1，

设直线PF2的倾斜角为θ，

则cosθ=cos(∠PF1F2+60°)

=cos∠PF1F2·cos60°-sin∠PF1F2·sin60°

由双曲线的焦半径公式

又a2+b2=c2，

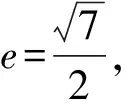
故选A.

点评利用正弦定理解出焦半径所在直线的倾斜角的余弦值，代入焦半径公式中得出a，b，c的关系，再配合a2+b2=c2，解出离心率.

不管解答哪一类试题都要掌握其实质，掌握其规律，规范其步骤，探究其变式.久而久之，学生的数学思维能力、数学解题能力、数学核心素养等定会有大幅度的提升.