2021年全国Ⅰ卷理科解析几何压轴题的多角度探析
2022-05-23彭耿铃
彭耿铃
(福建省泉州市第七中学;福建教育学院数学教育研究所 362000)
2021年全国Ⅰ卷理科解析几何压轴题,突出学科素养和区分导向,着重考查考生的运算能力以及综合运用数学思想方法分析问题、解决问题的能力,体现了解析几何压轴的应用价值,在考试评价中落实区分度的根本任务,对选拔高层次人才有很好的导向和选拔作用.
1 试题呈现

(1)求C的方程;
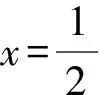
2 试题解析
2.1 第(1)问解析

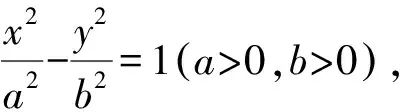


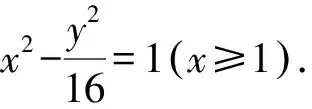
2.2 第(2)问解析

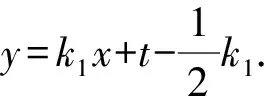

消去y并整理,得
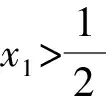
由韦达定理,得

设直线PQ的斜率为k2,同理可得
因为|TA|·|TB|=|TP|·|TQ|,
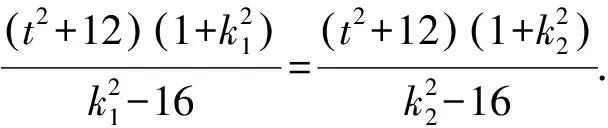
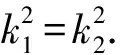
显然k1-k2≠0,故k1+k2=0.
因此,直线AB与直线PQ的斜率之和为0.
解法2(两根法) 同解法1,得
因为|TA|·|TB|=|TP|·|TQ|,
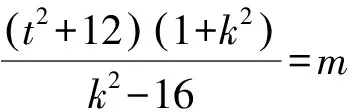
即kAB,kPQ为方程(t2+12-m)k2+t2+16m+12=0的两根.所以kAB+kPQ=0.
因此,直线AB与直线PQ的斜率之和为0.
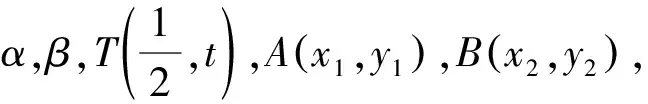

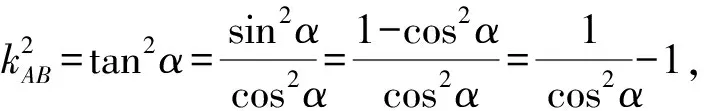

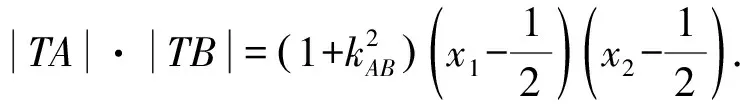
下同解法1,得

因为|TA|·|TB|=|TP|·|TQ|,
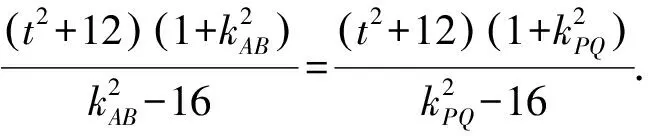

即(kAB-kPQ)(kAB+kPQ)=0.
显然kAB≠kPQ,故kAB+kPQ=0.
因此,直线AB与直线PQ的斜率之和为0.

(16m2-1)y2+32mny+16(n2-1)=0.
由韦达定理,得
所以|TA|·|TB|=(1+m2)(y1-t)(y2-t)
同理设直线PQ的方程为x=ay+b,
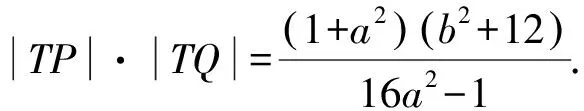
因为|TA|·|TB|=|TP|·|TQ|,
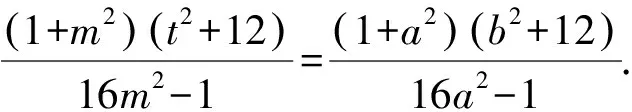
整理,得m2=a2.
即(m-a)(m+a)=0.
显然m-a≠0,故m+a=0.
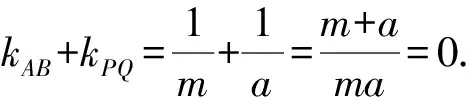
所以直线AB与直线PQ的斜率之和为0.
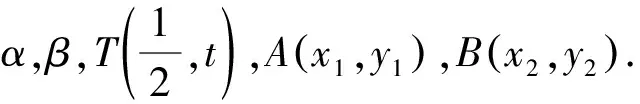
设直线AB的方程为x=my+n,直线PQ的方程为x=ay+b,则



所以|TA|·|TB|=(1+m2)(y1-t)(y2-t).
下同解法4,得
|TA|·|TB|=(1+m2)(y1-t)(y2-t)
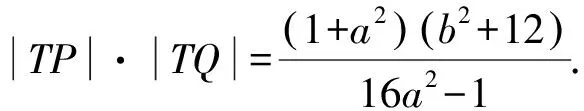
因为|TA|·|TB|=|TP|·|TQ|,
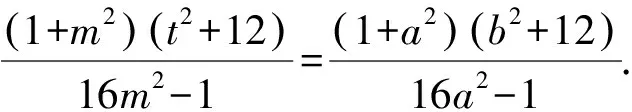
整理,得m2=a2.
即(m-a)(m+a)=0.
显然m-a≠0,故m+a=0.
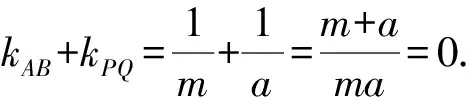
所以直线AB与直线PQ的斜率之和为0.
解法6(巧用圆系方程) 因为|TA|·|TB|=|TP|·|TQ|,
所以A,B,P,Q四点共圆.
设直线AB的方程为x=my+n,
直线PQ的方程为x=ay+b,
构造同时过A,B,P,Q四点的二元二次曲线系方程:λ(16x2-y2-16x)+(x-my-n)(x-ay-b)=0,
因为此方程表示的曲线为圆,
所以x·y的系数-(m+a)=0.
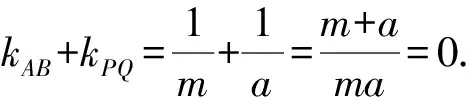
所以直线AB与直线PQ的斜率之和为0.
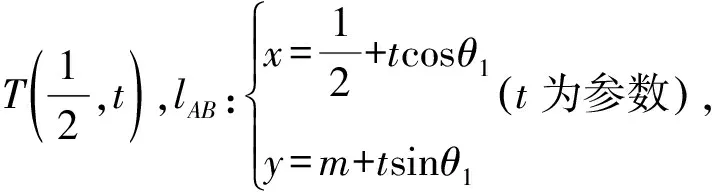
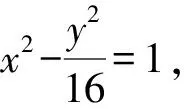
不妨设|TA|=t1,|TB|=t2,则
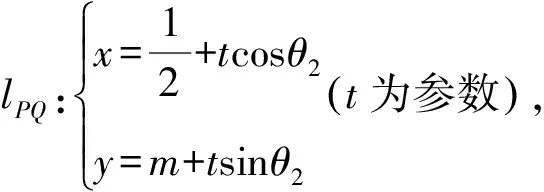
因为|TA|·|TB|=|TP|·|TQ|,

因为lAB和lPQ不重合,所以θ1≠θ2.
故θ1=π-θ2.
所以直线AB与直线PQ的斜率之和为0.

设T(0,n),lAB:y=mx+n,lPQ:y=kx+n,
得(16-m2)x2+(16-2mn)x-(n2+12)=0.
设A(x1,y1),B(x2,y2),则由韦达定理,得
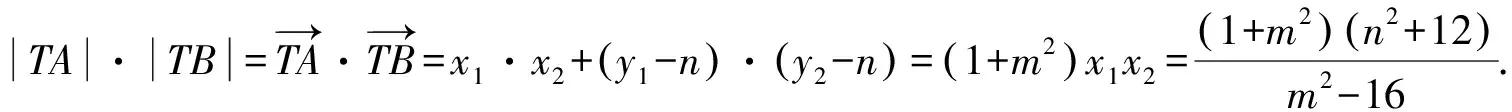
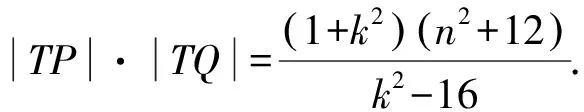
因为|TA|·|TB|=|TP|·|TQ|,
所以整理可得m2=k2.
即(m-k)(m+k)=0.
显然m≠k,故m+k=0.
因此,直线AB与直线PQ的斜率之和为0.
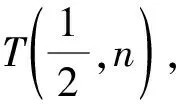
lAB:y=k1x,lPQ:y=k2x.

设A(t1,y1),B(t2,y2),则由韦达定理,得


因为|TA|·|TB|=|TP|·|TQ|,
即(k1-k2)(k1+k2)=0.
显然k1≠k2,故k1+k2=0.
因此,直线AB与直线PQ的斜率之和为0.
以上的九种证明方法从不同角度合理地解决问题,因此教师在日常教学中,应引导学生多视角思考,引导学生用不同方法来解决数学问题,引导学生以平易近人的思维探寻压轴题的解题思路,如何以自然而然的思维来解决压轴题,这样才能更好地培养学生的思维品质,提高学生运算、分析问题和解决问题的能力,从而提高学生的数学核心素养.
