紧抓基底 明辨真假“距离”——一道向量题的解法质疑与思考

刘稳殿

(陕西省白河高级中学 725801)

在讲解高三数学试卷时，用最简单、最迅速的办法解出小题是高三师生追求的共同目标，教师在讲解小题时惯性思维占去了部分思考空间，也为师生解题提供了简便快捷的通道.教师带领学生思考一个问题的多种解法，有利于学生思维的发散与知识的融合.但如果学生对问题的理解深度尚浅，学生自行钻研可能因为忽略条件走入误区，那么，此时对于小题进行大做不仅能够发现学生错因，而且能发现本题精髓及解题奥秘，更能进行拓展，开阔学生思维深度与广度，做以适当总结，即可明了知识点对应的解题类型与解题方法.以下探讨一道高三模拟的向量题：

图1

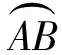
则x2+(y-1)2表示点(0,1)到点(x,y)距离的平方.

图2

所以，当点C在点A处时，x2+(y-1)2的值最大，为12+(0-1)2=2 .

图3

则x2+(y-1)2表示点(0,1)到点(x,y)距离的平方.

所以，当点C在点B处时，x2+(y-1)2的值最大，为02+(-1-1)2=4 .

质疑1两种解法思路相同，为何答案不同？

学生解答出现的问题是：

本题一般解法如下：

方法1 如图2所示，显然有

所以点A坐标为(1,0)，

点B坐标为(0,1)，

点C坐标为(x,y).

则x2+(y-1)2表示点B(0,1)到点C(x,y)距离的平方.

所以，当点C在点A处时，x2+(y-1)2的值最大，为12+(0-1)2=2 .

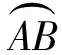
所以(x-1)2+y2=(cosθ-1)2+sin2θ

=2-2cosθ.

因为θ∈[0°,90°]，

所以cosθ∈[0,1].

所以当θ=90°时，cosθ=0,(x-1)2+y2取得最大值2.

质疑2式子x2+(y-1)2是表示点(0,1)到点(x,y)距离的平方吗？

图4

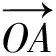
所以点A坐标为(1,0)，

点B坐标为(0,1),

点C坐标为(x,y).

则x2+(y-1)2表示点B(0,1)到点C(x,y)距离的平方.

所以，当点C在点A处时，x2+(y-1)2的值最大，为12+(0-1)2=2 .

图5

所以x2+(y-1)2≥2.

即x2+(y-1)2的最大值为2 .