岩体结构对岩质滑坡运动过程和堆积特征的影响研究

张恩铭，程谦恭,2，林棋文，谢 宇，王玉峰,2，姚志勇，孙先锋

（1.西南交通大学地质工程系,四川 成都 611756；2.高速铁路运营安全空间信息技术国家地方联合工程实验室（西南交通大学）,四川 成都 611756；3.中铁第一勘察设计院集团有限公司,陕西 西安 710043）

大型岩质滑坡具有高位、隐蔽性强和高速远程等特点[1-2]，严重威胁着周边及山前平原地区居民的生命财产安全[3-5]。近年来，我国深受这类灾害的威胁。2019年7月23日，贵州省六盘水市水城县鸡场镇山体斜坡，在持续降雨等影响下失稳启动，随后演化为碎屑流，携带着巨大能量进行刮铲和堆积，沿途冲击和掩埋多处居民建筑，最终造成约1 600 余人受灾、20 余幢房屋被埋、43 人遇难、9 人失联，造成直接经济损失约1.9 亿元[6]。2008年5月12日汶川8.0 级大地震诱发了大量的大型岩质滑坡，其中发生在青川县的东河口滑坡，在短时间内以大于20 m/s 的速度冲入前沿的红石河，并在对岸爬高70 m 后继续向前滑行1.5 km，摧毁了整个东河口村，约700 人被掩埋[7]。2009年6月，重庆市武隆县发生大规模滑坡，体积约为50×106m3的岩体发生整体滑移，运动速度极快，并在较短时间内迅速解体，越过坡体前缘沟谷后冲向对岸。由于对岸山体的阻挡作用，大量滑体物质转向，沿沟谷向下游运动，形成长2 200 m，厚30 m 左右的堆积区，导致12 幢房屋损毁，并且掩埋正在开采的矿井入口，造成10 人伤亡，64 人失踪，8 人受伤[8]。由此可见，大型岩质滑坡破坏性极强且发生突然，应充分了解其致灾范围，在早期对其进行识别并提前防范，将灾后损失降到最低。因此，十分有必要对岩质滑坡运动距离和堆积特征进行相关研究。

目前关于岩体结构对滑坡运动和堆积过程的影响尚未充分研究，已经存在的动力学模型及其数值模拟方法也很少考虑岩体结构[9]。但是岩体结构往往伴随整个大型岩质滑坡的滑动过程，控制破坏机制与运动方式。在滑坡源区，岩体被结构面切割成不连续体，其运动特征同完整岩体有很大区别，不同产状、规模、组合情况和粗糙程度的结构面切割后的块体的运动特征和堆积特征也各不相同[10]。Pollet 等[11]在现场调查中发现Flims 滑坡源区滑体为巨型块状灰岩，在运动过程中虽发生一定程度的破碎，但堆积体的岩层层序仍与源区的层序极为相似；而发生在四川茂县的新磨村滑坡，由于该处倒转褶皱和断裂较为发育，因此源区岩体中包含多组结构面，滑体在滑动过程中不断发生破碎，转变成高速碎屑流向下运动，经不断的碰撞耗能最终沉积下来[2,12-16]。可见，岩体结构差异会使得滑体表现出不同的运动形式和能耗模式，使得致灾范围有着显著区别[17]。所以明确源区不同结构类型岩体对大型岩质滑坡运动距离和堆积特征的影响规律是十分有意义的[18]。

近年来，部分学者在滑坡运动的相关研究中考虑了岩体结构的影响。Manzella[19]通过使用相似块体和碎屑颗粒进行室内试验，发现源区中堆叠整齐的块体的运动速度要快于随机叠放的相似块体和松散碎屑颗粒的运动速度，并且有着更远的运动距离；Bowman等[20]通过使用含有结构面的煤块，在离心机内小规模再现脆性岩体的动力破碎过程；Haug 等[21]使用相似块体进行室内试验，通过改变物源区相似块体的高宽比等条件，发现源区块体的不同结构最终会直接影响滑块的破碎程度，并间接影响其运动距离；Charrière等[22]通过现场对Frank 滑坡进行调查，发现源区岩体结构面在滑坡动力破碎过程中起着至关重要的控制作用，并且也影响滑坡堆积体表层堆积特征；Lin 等[23]使用可破碎的相似块体进行室内试验，通过改变源区相似块体的节理组数、节理方向等条件，发现初始结构对破碎程度等有极大影响。目前这些研究主要集中于讨论岩体结构对破碎程度的影响，并且考虑岩体结构的形式较为单一。为了充分考虑不同岩体结构对运动距离和堆积特征的影响，本文以乱石包滑坡为依据进行简化，采用相似材料进行物理模型试验，数值模拟的尺寸完全还原室内物理模型试验，数值模拟中材料的参数根据单轴压缩试验结果进行校正，摩擦和阻尼根据实际情况进行设置。经验证，数值模拟可以较为准确的重现室内试验结果，具有合理性。

在上述基础上，本文设置了四种工况，使用离散元数值模拟方法，通过模拟不同结构面强度、结构面密度、结构面方向和岩块强度下岩质滑坡碎屑化运动过程，研究了结构面和结构体特征对岩质滑坡破碎特征、运动形式和运动距离的影响规律及影响机制。

1 研究方法

1.1 试验及工况设置

数值模拟模型是以室内斜板试验为依据建立的，通过对滑坡进行简化，室内斜板试验主要包括：物源区，由透明亚克力板围成；运动区，1 m×3 m 的斜板；堆积区，2 m×3 m 的水平底板（图1）。

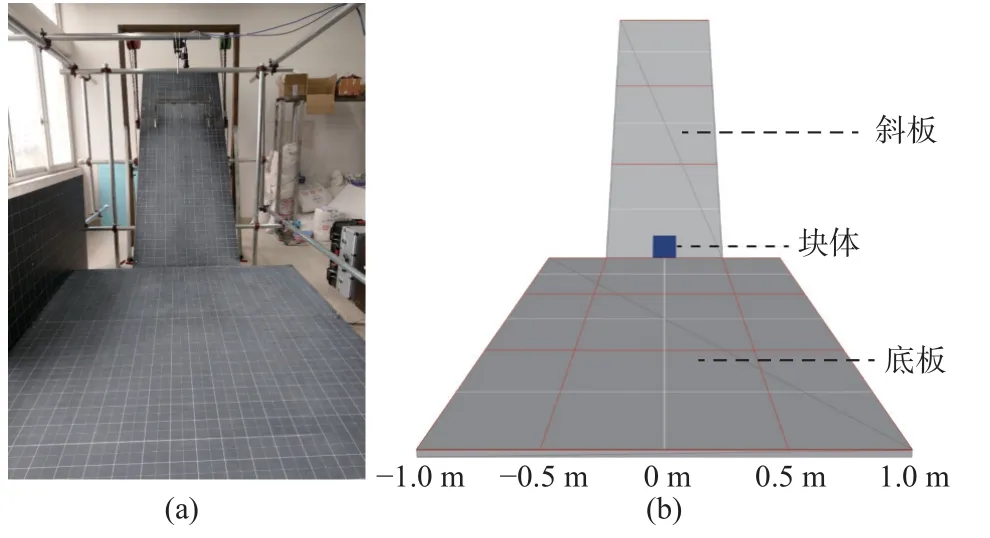
图1 （a）室内试验装置和（b）斜板试验数值模拟模型Fig.1 (a) Experimental setup and (b) numerical simulation model diagram of inclined plate experiment

相似块体以乱石包滑坡岩体为原型，依据量纲分析计算出的相似材料理论强度参数，再选取相应的原材料进行制样，制得的相似材料可以基本满足理论力学特征。有关试验装置、相似材料和相关物理模型试验可以参考之前的工作[24]。

整个试验过程包括无初速度的释放源区物料，使相似块体沿斜板向下滑动，斜板与地板转折处正上方的高速摄影机（baumer VCXU-02M）记录转折处的撞击过程，斜板装置的正前方和水平底板上堆积区正上方分别设有照相机（尼康D7000）记录运动过程。

为了充分研究岩体结构对滑坡运动过程和堆积形态的影响，本文用数值模拟的方法，主要对结构面强度、结构面密度、结构面方向和岩块强度进行研究。设置工况如表1，单个完整块体的尺寸为200 mm×200 mm×36 mm，通过改变模型结构面5 mm 内的黏度值模拟不同强度的结构面。以结构面强度为研究对象时，结构面的黏度值不断增大；以岩块强度为研究对象时，令结构面黏度值恒定，使岩块黏度值不断增大；以其他参数为研究变量时，结构面黏度值保持不变（具体设置见表1）。

1.2 DEM 模型的建立

本文使用数值模拟软件PFC3D 对岩体失稳运动过程进行模拟。将PFC3D 中的基本单元球（ball）经黏结组成的整体模拟颗粒材料，在颗粒材料周围以墙（wall）围成其边界（主要采用的黏结模型为线性模型和线性平行黏结模型）。颗粒材料的宏观性质通过集合体中球的运动和相互作用决定。PFC3D以牛顿运动定律和力与位移定律为基础。通过循环计算更新颗粒之间接触力及颗粒位移关系[25-26]。每一个时步对应一种状态。在动态模拟中，时步值很小，每个时步内颗粒只会和相邻颗粒产生相互作用，并不会对其他颗粒产生影响，颗粒的宏观运动由每个时步的位移和力的累计确定。

PFC3D 中宏微观参数并非完全对应。因此，在数值模拟之前应该先对微观参数进行标定，一般常用单轴压缩试验和巴西劈裂试验等[27-28]。本文通过单轴压缩试验获得相似块体的宏观参数（泊松比，抗压强度等），再通过试错的办法来调整微观参数值，使模型的宏观参数满足要求，来标定黏结模型的微观参数值（表2）。图2（a）是数值模拟试样和室内试验试样的应力应变曲线对比图，图2（b）是模拟试样和试验试样的破坏形式，从中可以看出二者具有相似的破坏形式，并且应力应变曲线也有着相似的趋势。

图2 （a）相似材料的应力应变曲线对比图和（b）单轴压缩试验下相似材料破坏特征图Fig.2 (a) Stress-strain curves of the block in DEM simulations and experiments and (b) fracture characteristics of samples in the uniaxial compressive test of laboratory and DEM simulation

离散元模型中，斜板规格完全还原室内试验的规格，如图1。选用墙单元作为水平底板和斜板，相似块体材料由球（ball）组成，接触本构模型选用平行黏结模型。结构面的设置方法采用Zhao 等[29]给出的建议，通过对结构面约4～5 mm 范围内的颗粒去掉黏结来实现。与物理模型试验不同，颗粒材料不是在斜板顶部释放，而是在转折端以3.75 m/s 的初速度释放，如图1（b）中蓝色块体所示，初速度是通过物理模型试验在同一位置获得的，这样做是为了消除相似材料在斜板上滑动过程中发生旋转所带来的误差。离散元模型中主要由施加阻尼和摩擦进行能耗，摩擦取值为0.577，与物理模型试验中取值一样；此外，通过与完整块体室内斜板试验的结果对比，当数值模拟宏观参数与试验结果一致时，确定数值模拟微观参数值（表2）。

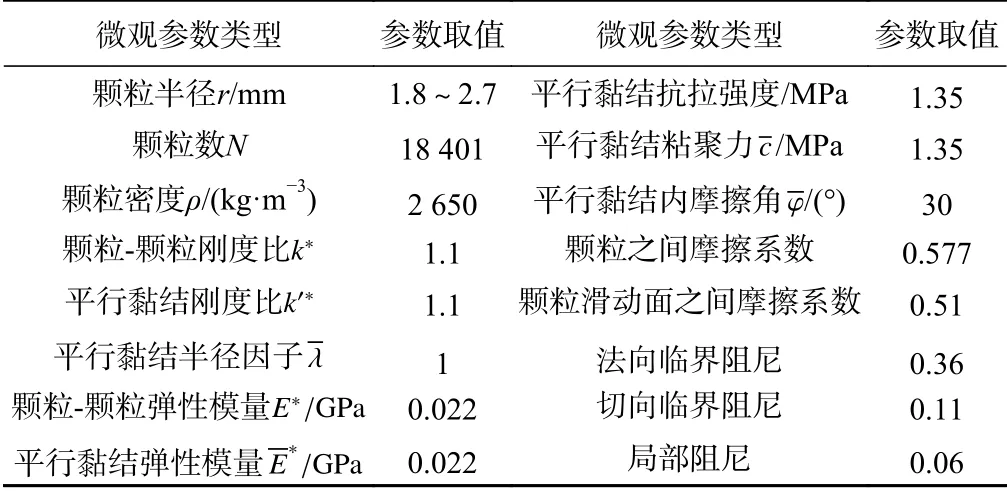
表2 数值模拟微观参数值Table 2 Calibrated values of the input micro-parameters of the numerical simulations

1.3 模型验证

本小节对完整工况进行一次数值模拟，并从堆积形态、粒径分布等方面进行对比及讨论，主要考虑的参数有前缘运动距离Lf、质心运动距离Lg、分布面积Sa和相对破碎率BR[30]，再将Lg、Lf和Sa进行无量纲化处理，便于统一对比。其中Lg为滑块运动前后质心之间的水平距离；Lf为堆积体最前端与滑缘最后端之间的水平距离；L为滑块沿斜面下滑长度；h为滑块厚度；l为滑块长度；为了便于统计将颗粒累积质量占比为95%所处的位置定义为堆积体最前端；分布面积Sa的算法为：Sa=w·Ls，其中w定义为堆积体两侧颗粒累积质量占比分别达到95%所处位置之间的距离，Ls为块体最前端与转折段之间的水平距离（图3）；相对破碎率[20,31]是评估块体破碎程度的一种量化指标。

图3 模型参数示意图Fig.3 Schematic diagram of model parameters

从图4（a）堆积形态对比图可以看出，物理模型试验和数值模拟的堆积特征具有一致性，粒径分布为大块体（绿色）居多，碎屑颗粒（蓝色）较少且分布在底面，较大的块体主要集中在转折端附近。由图4（b）的运动参数可以看出，试验和模拟的Lg和Sa基本可以保持一致，数值模拟中Ls偏大，这是因为数值模拟中破碎岩体破碎成基本单元（ball）后，无法继续发生破坏，且运动性更高，导致了Ls稍大。

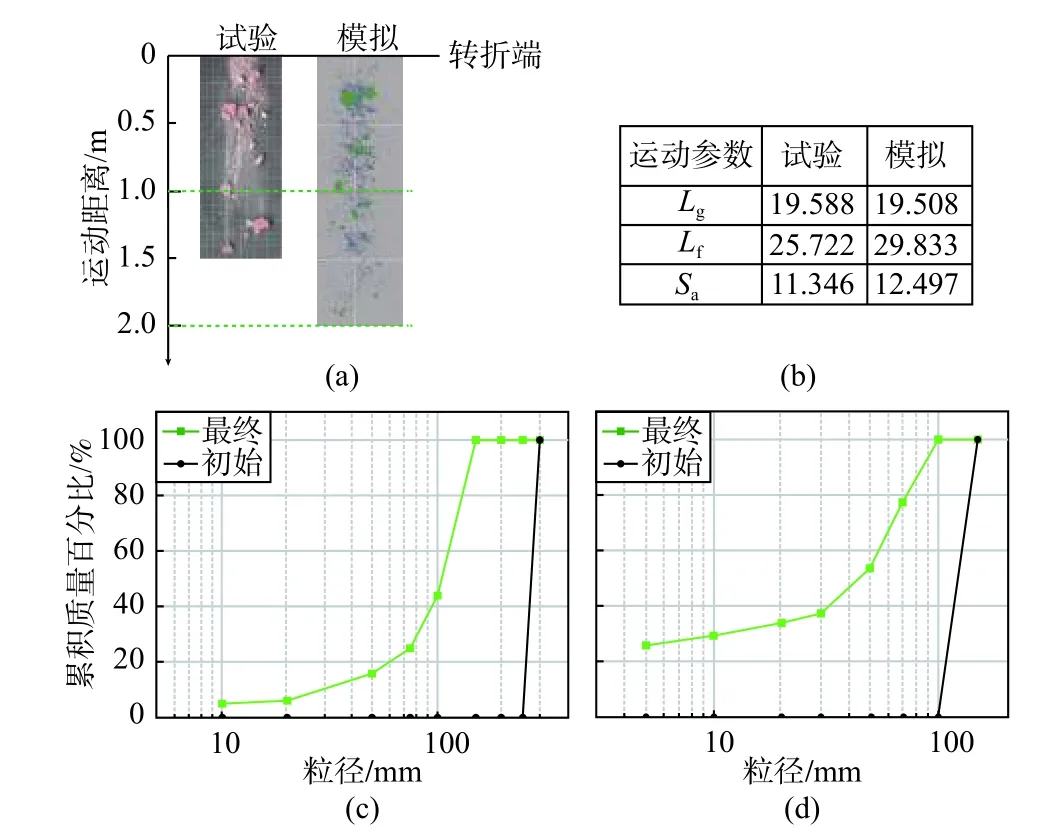
图4 （a）试验与模拟堆积特征对比、（b）主要参数、（c）试验与（d）模拟初始及最终粒径分布图Fig.4 (a) Deposit characteristics of intact block in the DEM simulations and experiments，(b) major parameters，(c)fragment size distribution of intact block in the DEM simulations and (d) fragment size distribution of intact block in experiments

由于上述问题导致数值模拟中无法采用常规方法统计粒径，因此本文采用如下方法统计数值模型的粒径[30]，具体算法如式（1）：

式中：Deq,i——模型中等效粒径/m；

Vi——体积/m3。

图4（c）与图4（d）反映出室内试验和数值模拟两者的粒径分布规律基本一致，但是因为数值模型中颗粒半径以及颗粒数无法对室内试验做到完全还原，且数值模型中的最小单元无法继续破坏，所以模拟中统一将最小单元的质量都归于5 mm 内，这也就导致模拟工况的粒径分布与试验工况略有不同，且破碎率0.278 也大于室内试验计算得到的0.155。

通过对比分析，验证了数值模拟的结果经过处理可以较为准确的拟合物理模型试验的结果，并且可以对各种试验条件进行理想化处理，避免试验中的人工误差，也可以通过数值模拟研究室内试验难以观察到的其他现象，因此该模型可以很好地模拟室内斜板试验。

2 影响因素分析

2.1 结构面强度

岩体结构面强度的变化对岩体的破坏形式起着控制作用。一般来说，当结构面强度较低时，块体先顺着结构面产生破坏，进而破坏扩展到整体；当结构面强度增大时，结构面和岩块可能会一起发生破坏，甚至岩块先于结构面发生破坏。图5 表现了不同结构面强度下，岩块在碰撞转折段瞬间（t=0.002 5 s）的裂纹分布特征及沉积形式，其中岩块强度恒定。从裂纹分布图中可以看出，无论结构面强度的高低，岩块前端的底部都分布极多的裂纹，这说明在受到碰撞之后，前端底部相较于其他部位的破碎更为严重。观察低结构面强度工况（SJ-0.05）可知，碰撞时裂纹大多集中于结构面，说明破坏是沿着结构面发展的，结构面贯通，岩体发生破坏。随着结构面强度逐渐变高，块体后部的水平向（顺层）结构面和纵向结构面处产生的裂纹逐渐减少，结构面贯通程度降低，块体后部的裂纹也逐渐变少，前部裂纹逐渐变得密集并开始出现较明显的连续裂纹，岩体破坏形式发生改变。对于横向结构面而言，SJ-0.05 到SJ-0.3 中大量裂纹都集中于横向结构面上且横向结构面贯通，在SJ-0.5 中由于结构面强度较高，横向结构面并未贯通，裂纹也是断续产生的，这会使块体作为一个整体的运动时间长于结构面强度较低的工况。

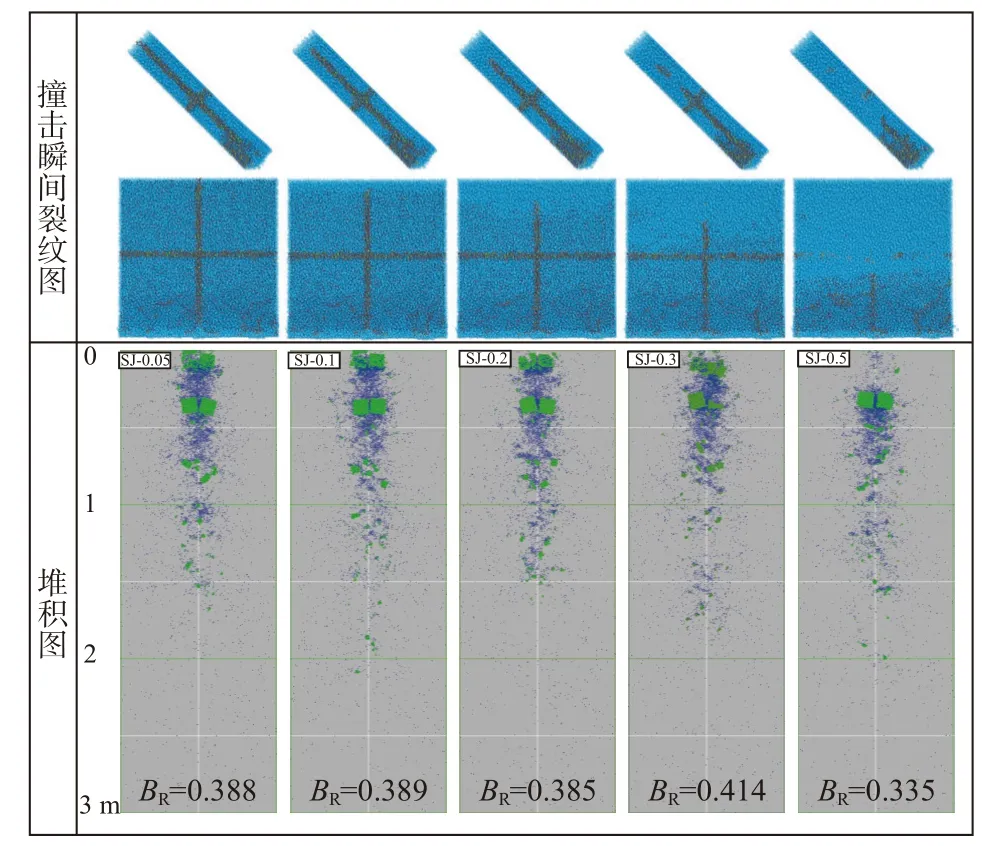
图5 不同结构面强度下撞击瞬间裂纹分布及最终堆积图Fig.5 Crack distribution and deposit characteristics of sliding masses with different joint strength

对于SJ-0.05、SJ-0.1 和SJ-0.2 工况而言，破碎率都较为接近，分别为0.388、0.389 和0.385，且最终堆积形态基本一致，说明结构面强度较低时，结构面控制着岩体的破坏形式和堆积形式；同SJ-0.3（BR=0.414）和SJ-0.5（BR=0.335）工况相比，堆积形态同结构面强度较低的工况有较大差别，这也说明结构面强度较高时，块体的破坏形式和堆积形式由结构面和结构体共同控制，破坏不仅发生在结构面处，也发生在块体的其他位置。因此，结构面强度变大，裂纹变稀疏，块体后部的破坏程度降低。

从图6 可以看出Lf和Sa与结构面强度的相关性不大，结构面抗拉强度对Lf的影响幅度在4%左右浮动，而对Sa的影响幅度在14%左右，说明结构面抗拉强度的大小对于块体的运动形式具有一定程度的影响；Lg随结构面强度的增加而增加，结构面抗拉强度提升10 倍，Lg增加3%，工况SJ-0.5 的Lg最大，这是因为结构面抗拉强度较大，撞击瞬间横向结构面并未完全未贯通，块体作为一个整体的运动时间较长，因此标准化质心运动距离较大。

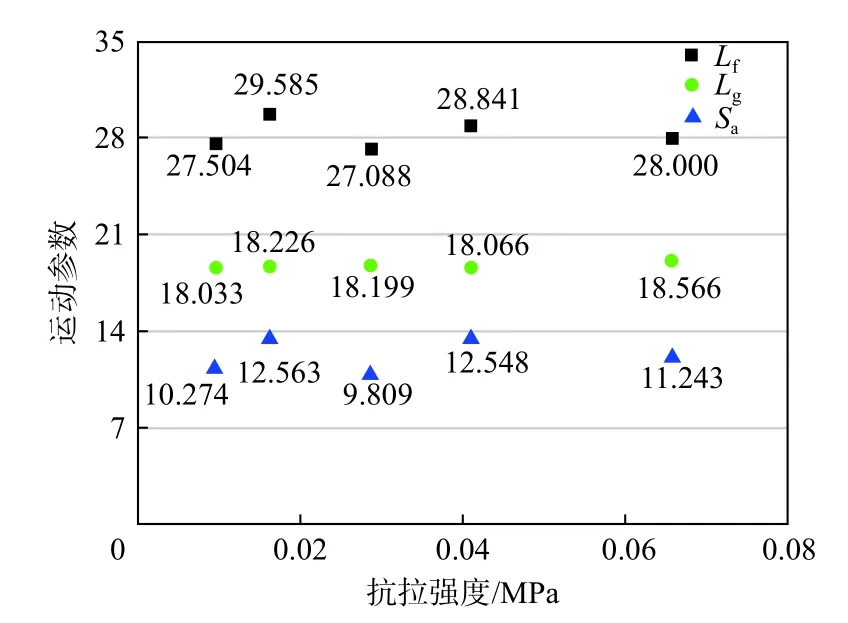
图6 运动参数随结构面抗拉强度的变化Fig.6 Motion parameters of different joint strength

2.2 结构面密度

图7 是不同结构面密度工况的最终堆积形式。从图中可以看出M1 工况完整岩体破碎后形态各异，而M2 和M3 工况块体破碎后还有部分较为完好的保持原始块体的形状，这种堆积形式表明破坏更容易沿着结构面发生；此外可以看出M1 工况块体在碰撞过后继续向前运动了一定距离再开始堆积，而M2 和M3工况块体则是一经碰撞，立马在原地进行堆积，甚至有部分块体滞留在转折端上部区域，这也表明结构面对于岩体堆积位置有着明显的影响；从破碎率可以看出，结构面密度越大，岩体破碎率越高。

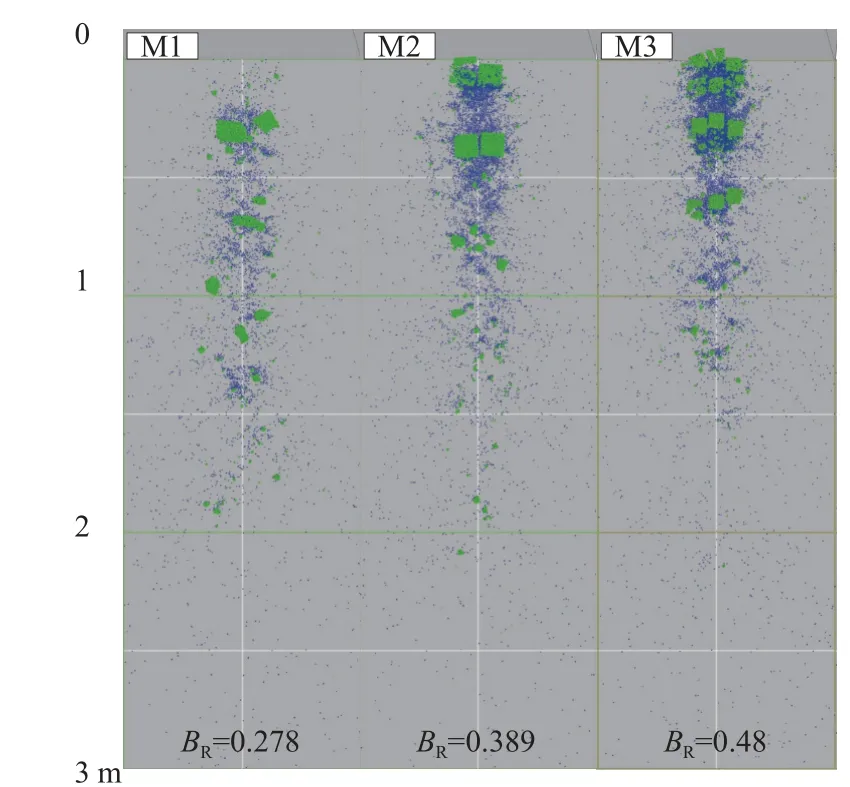
图7 不同结构面密度堆积图Fig.7 Deposit characteristics of sliding masses with different joint densities

图8 是不同结构面密度工况BR随时间变化的关系。由图可见破碎主要是发生0～0.05 s 之内，后续的破碎相对较小，可以忽略不计，说明块体与转折端的碰撞是产生破碎主因。另外，碰撞后较短时间内，破碎率与结构面密度呈正相关，即碰撞时结构面密度越大，破碎程度也就越高。

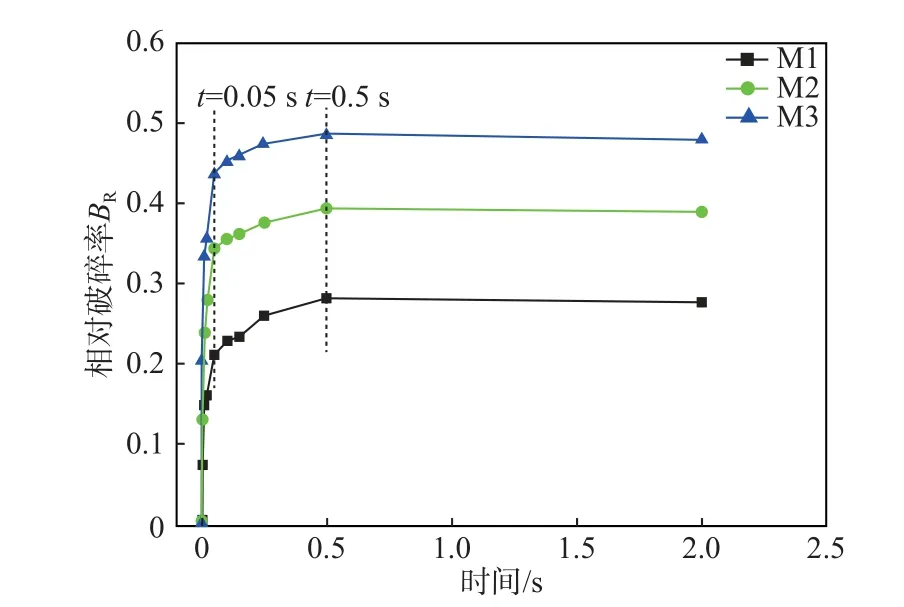
图8 不同结构面密度工况下BR 随时间的变化Fig.8 Relative breakage ratio versus time under different joint densities

从图9 可以看出随着结构面密度不断增大，Lg逐渐减小，而对前缘运动距离Lf和Sa并没有显著影响；当结构面密度进一步增大时，Lf和Sa都表现出骤降的趋势。因此，当结构面密度增加到一定程度时，块体的各项运动参数都呈下降趋势，且块体的破碎程度会增大。

图9 不同结构面密度工况下运动参数图Fig.9 Motion parameters of different joint densities

2.3 结构面方向

图10 是不同结构面方向工况堆积图，图11 是不同结构面方向工况运动参数图。从图10 中可以看出三种不同工况的堆积形式各不相同。D1 是横向结构面块体，块体被结构面分割成前中后三部分，破碎程度从前往后依次降低，且后部块体较为完整，这表明由于前部块体的阻挡，后部块体在撞击转折端时的速度较低，不足以发生破碎；D2 是纵向结构面块体，块体被结构面分割成左中右三部分，最终堆积形式具有一定的对称性，各部分破碎形式较为相似；D3 是水平向结构面（顺层）块体，块体被结构面切割成上中下三层，破碎程度较大，在转折端处有较多堆积，说明下层块体在上层块体和转折端的约束下，撞击时的速度较小。D3 工况堆积体中碎屑颗粒（蓝色）明显多于D1与D2 工况，三种工况的破碎率大小关系为：D1＜D2＜D3，说明顺层岩块破碎的可能性更高。

图10 不同结构面方向工况下堆积图Fig.10 Deposit characteristics of sliding masses with different joint directions

由图11 中可知，D1 和D2 的运动参数比较接近，对于D3 工况而言，Lg与Lf均降低10%左右，Sa则缩减接近30%。这表明顺层岩块在发生碰撞后更易发生破碎且破碎程度更大，并且层间咬合与摩擦会产生极大的能耗，最终使得运动距离变近，Sa降低。

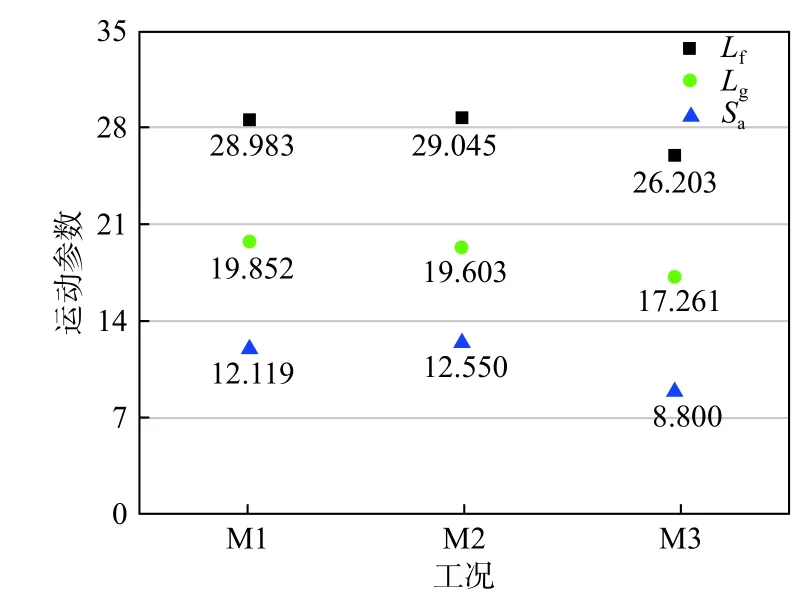
图11 不同结构面方向工况下运动参数图Fig.11 Motion parameters of different joint directions

2.4 岩块强度

影响堆积形式和破碎程度的因素除结构面参数外，岩块本身的强度也是不可忽略的。图12 和图13是不同岩块强度工况的最终堆积图，从图中可以看出，S1-0.5 和S2-0.5 都存在着大量的单个颗粒，分布在堆积体底部，表面只有极少数的块体分布，破碎程度很高，破碎率分别为0.503 和0.564，当岩块强度不断增大时，堆积体主要以大尺寸块体为主，碎屑颗粒数目逐渐减小。同时在岩块强度相同的情况下，结构面块体S2 的破碎率要始终高于完整块体S1，这说明岩块强度恒定，结构面会使堆积体的破碎程度有所增加。

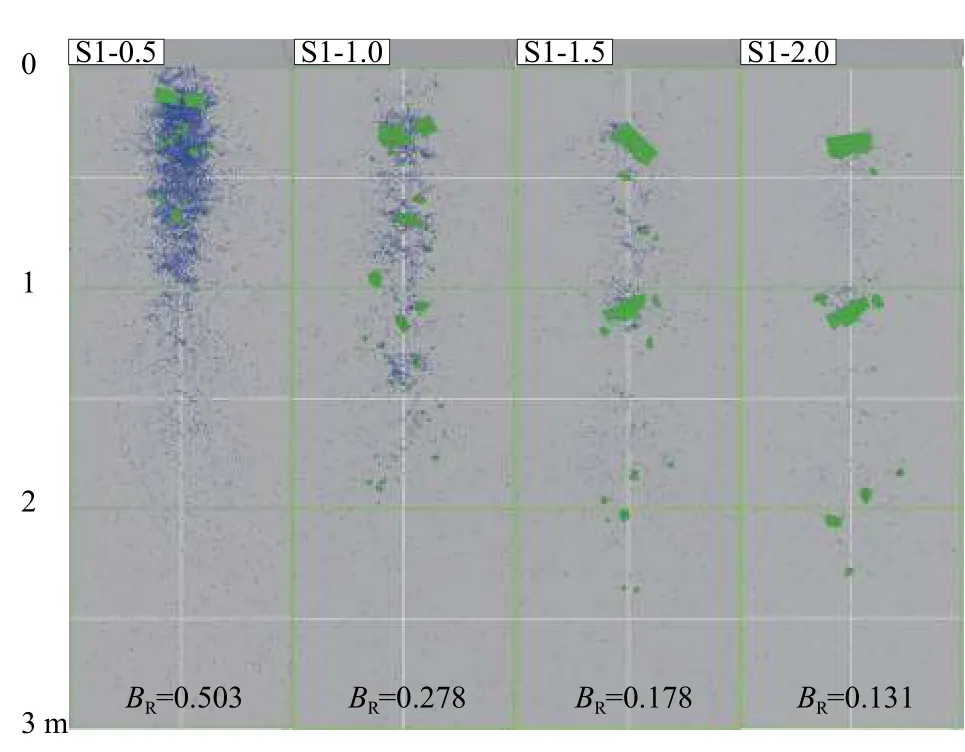
图12 不同岩块强度下S1 工况堆积图Fig.12 Deposit characteristics of S1 with different block strength

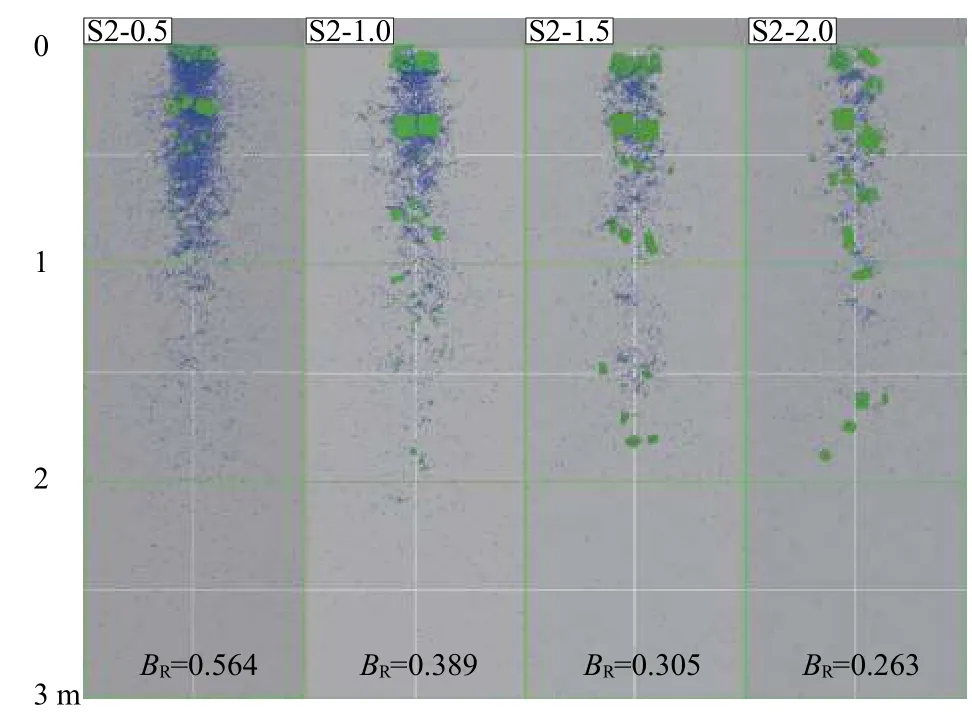
图13 不同岩块强度下S2 工况堆积图Fig.13 Deposit characteristics of S2 with different block strength

图14 为工况S1、S2 的岩块强度与运动参数之间的关系，当岩块强度不断增大，S1（完整岩体）和S2（含结构面岩体）的Lg也随之变大，但完整岩体工况的增幅为15%左右，比含结构面岩体工况增幅明显。由图14 可知，完整岩体工况在低强度时，一经碰撞就立马在原位进行堆积。而岩块强度增加时，块体先运动一定的距离，然后停积；而含结构面岩体工况在不同强度下，一经碰撞就立刻就地堆积一部分。这说明结构面的存在会显著影响岩体的堆积形式，大幅度降低堆积体后缘运动距离。岩块强度的增加使得S1 的Lf也有所增大，增幅为15%左右；而工况S2 的Lf先升再降，且当岩块强度较大时，S1 的Lf大于S2 的Lf。就分布面积Sa而言，岩块强度的不断增大，使得Sa先快速下降后趋于稳定，最终缩减了约40%左右。

图14 S1、S2 工况岩块强度与运动参数关系图Fig.14 Motion parameters of S1 and S2 with different uniaxial compression strength of block

3 讨论

对于斜板数值模拟试验的建模模型而言，斜板可以看作是倾斜的滑动面，底部平板可以看作是无侧限的堆积区，整个运动过程可以描述成结构面岩体在平直的倾斜滑动面经加速后撞击底面，在平面撒开区无侧限的进行运动和堆积的全过程，根据Hutchinson[32]的分类依据，斜板数值模拟试验可以看作平移型滑动。尽管模拟较为简单，不足以涵盖自然界中滑坡的所有复杂的运动要素，但对于滑坡的运动过程和堆积形式的初步研究是合理并可行的[20-21,33-34]。

在前面的研究中，可以看出岩体结构伴随整个大型岩质滑坡的滑动过程，控制着滑坡的破坏机制与运动方式。由于岩质滑坡结构面中胶结程度的不同，导致结构面强度有着显著差别，由模拟结果可知，在结构面强度较低的情况下，结构面的存在会影响到Lf、Lg和Sa，但并没有表现出较为明显的趋势，而当结构面强度较高时（SJ-0.5），Lg增大。之所以有这样的结果，首先因为结构面强度增加，破碎率明显降低，由于破碎而引起的能量消耗也随之减少，因此质心运动增加，另外由于较高的结构面强度，使得块体在撞击转折端的瞬间横向发育的结构面并没有贯通，破碎时间延后，在水平底板上保持相对完整的形态运动了一段时间，这期间破碎颗粒之间相互作用所消耗的能量低于前面几组工况，因此有较大的Lg。就结构面密度而言，结构面密度越大，表明岩体所处的应力环境越复杂，可能同时或先后经历过多次强烈的构造作用，其性质较原岩可能会有很大改变，如M3 工况相较于M1工况，岩体性质更为脆弱，一旦失稳，在运动过程中更易破碎（图9），且破碎过程发生在整个运动全过程，在撞击地面时尤为突出，又由于破碎导致运动过程中颗粒之间相互作用导致能量消耗[23]，导致Lf和Sa降低，符合De Matos[35]提出的大型岩质滑坡运动过程中碎屑化进程受结构面密度影响的观点。这表明对于结构面密度较大的岩体在失稳滑动后的运动距离和分布面积均有一定程度的减小。对于顺层结构面工况D3 而言，岩体被结构面切割成薄层状，层与层之间的摩擦和咬合作用消耗大量的能量，并且在撞击时更容易发生破碎，使得Lf和Lg降低，这印证了Locat 等[36]和 Crosta 等[37]的结论。与此同时，影响滑坡运动过程和堆积体最终形式的还有岩体强度，较低强度岩体而言，岩体强度较高的滑体其Lf和Lg也有一定程度的提高，反之，Sa会在一定限度内降低，这是因为强度较大的岩体在运动过程中产生额碎屑颗粒较少，其内部由于颗粒间相互作用而造成额能量消散程度较低，最终导致较长的运动距离。

Haug[38]建立了物理模型试验尺度下块体破碎程度与滑坡运动距离的经验关系，并与真实滑坡进行对比。其中，块体破碎程度用mc表示，即试样总质量M与破碎后最大块体的质量mmax之比。我们将数值模拟结果与Haug 的模型试验和真实滑坡进行对比，绘制了图15。图中，蓝色曲线是Haug 根据其经验公式（式2）代入合适参数后绘制的拟合曲线；黑色曲线是选取本文数值模拟的对应参数，基于Haug 经验公式绘制的模拟结果拟合曲线。从对比图中可观察到，数值模拟中破碎块体的运动距离整体小于物理模型试验，其原因在于我们的模拟使用了相对较高的底面摩擦系数，以及数值模拟中块体破碎消耗更多的能量[24]。Haug 的试验结果显示，当m＜5 时，H/D（源区岩体后缘距水平面垂直距离H，源区岩体后缘距堆积体前缘水平距离D）呈下降趋势，运动距离增长，堆积范围增加；当m＞5 时，由于破碎程度进一步增大，加剧了颗粒之间相互作用，导致耗能逐步增加，运动距离有所减小，H/D开始缓慢增长。而数值模拟结果显示，整体上随破碎程度增加，H/D逐渐上升，与Haug的分析一致，说明破碎有助于滑坡在堆积区扩散更大的范围。真实滑坡破碎程度与运动距离显示出极大的离散性。因此，可以认为，摩擦系数控制了滑体的运动距离，而破碎程度进一步影响滑体的扩散范围，两者共同作用，最终决定高速远程的滑坡危害区域。

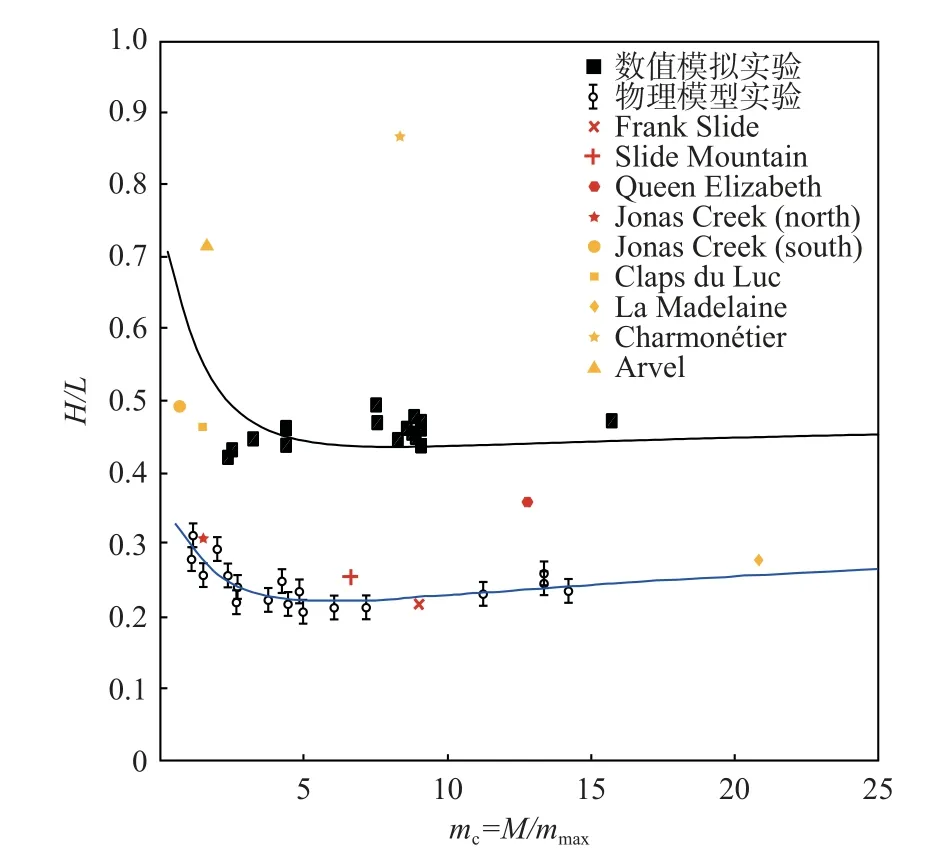
图15 破碎度与表观摩擦系数关系图Fig.15 Heim’s ratio for experiments with different degrees of fragmentation

其中，根据Haug[21]文中建议，令α=0.11，β=0.68，γ=2.0；根据试验设置，令µ=0.51，θ=45°。

数值模拟中还有一个比较重要的现象，当岩体强度相同时，结构面的存在会影响相对破碎率的大小（图13、图14），结构面岩体工况S2-2.0 的相对破碎率明显高于完整岩体S1-2.0，但是随着破碎程度的增加，Lf和Lg都出现了不同程度的降低，这同Haug 等[21]室内试验得出的结论相反，并且也不符合Bowman[20]论文中所总结的真实案例的现象。造成这样的结果是因为数值模拟中颗粒数较少（相较于物理模型试验），所以颗粒间连接的断裂需要耗费更多的能量；并且数值模拟中粒径的统计也同物理试验存在区别，这就导致离散元模型无法较为准确的模拟碰撞过程中滑体前端底部的局部塑性变形和冲击力[24]。因此在后续的研究中应该进一步完善参数标定的方法，使数值模型更为准确。

4 结论

在自然条件下滑体通常以不连续体的形式存在，其中存在着大量的结构面，结构面的各种属性及岩块强度等因素都会影响岩质滑坡的运动距离和堆积特征。通过对不同结构面强度、结构面密度、结构面方向和岩块强度下岩质滑坡碎屑化运动过程进行离散元数值模拟，研究了结构面和结构体特征对岩质滑坡破碎特征、运动形式和运动距离的影响规律及影响机制。主要研究结果如下：

（1）岩体结构面强度的变化对岩体的破坏形式起着控制作用。一般来说，当结构面强度较低时，块体先顺着结构面产生破坏，进而破坏扩展到整体；当结构面强度增大时，结构面和岩块可能会一起发生破坏，甚至岩块先于结构面发生破坏，且块体后部的破坏程度降低。结构面抗拉强度由小变大，Lg整体呈现出增大趋势。结构面抗拉强度对前缘运动距离Lf的影响幅度在4%左右，而对分布面积Sa的影响幅度在14%左右；Lg随结构面强度的增加而增加，结构面抗拉强度提升10 倍，Lg增加3%。

（2）Lf、Lg和Sa在结构面密度较高时，与结构面密度呈负相关；块体的相对破碎率与结构面密度呈正相关，破碎主要发生在撞击转折端瞬间，且破坏首先沿结构面方向产生。

（3）水平向结构面岩体的破碎率要大于其他方向结构面岩体的破碎率。与其他方向结构面岩体相比，水平向结构面岩体的Lf和Lg均降低10%左右，Sa则缩减接近30%，这表明顺层岩块失稳后破碎的可能性更大，同时破碎程度更高，并且层间相互作用会产生大量能耗，使Lf、Sa降低。

（4）岩块强度增加，使堆积体中单个颗粒的数目减少，堆积体主要以大尺寸块体为主，破碎程度减小。岩块强度恒定，结构面会使堆积体的破碎程度增加。岩块强度与完整块体工况S1 的Lf和Lg呈正相关，且最终增幅在15%左右，均大于结构面岩体工况S2 的增幅。对于Sa，S1 和S2 均快速下降后保持稳定，岩块强度增大到一定程度时，Sa不再发生明显变化，最终缩减了约40%。