天体运动中的3个时间问题的思考

牛书强

（乌鲁木齐八一中学，新疆 乌鲁木齐 830000）

1 圆周运动中的时间问题

圆周运动的追及相遇问题较为常见，但是在教学中发现月球环绕地球一周只有27.3天，并不是30天，引起了我的思考.

问题1.当地球位于太阳和木星之间且三者几乎排成一条直线时，称之为“木星冲日”，2016年3月8日出现了一次“木星冲日”.已知木星与地球几乎在同一平面内沿同一方向绕太阳近似做匀速圆周运动，木星到太阳的距离大约是地球到太阳距离的5倍，则，下一次的“木星冲日”时间在哪一年？

问题2.我们知道，一个月大约是29.5天，但是月球绕地球公转一周并不是29.5天，而是27.3天，两个时间为什么会不同？

所谓一个月是指相继两次满月的时间间隔，满月时太阳，地球和月球在同一直线上，若近似认为月球绕地球公转与地球绕太阳公转的轨道在同一平面内，而且均为正圆，又知这两种转动同向，相继两次满月时，太阳、地球和月球的相对位置示意图如图1.

图1

2 椭圆运动中的时间问题

2021年高考中出现了椭圆的周期求解，这引起的我对椭圆运动的时间的思考.

问题1.椭圆运动的周期.

问题2.运动1/4椭圆所用的时间.

图2

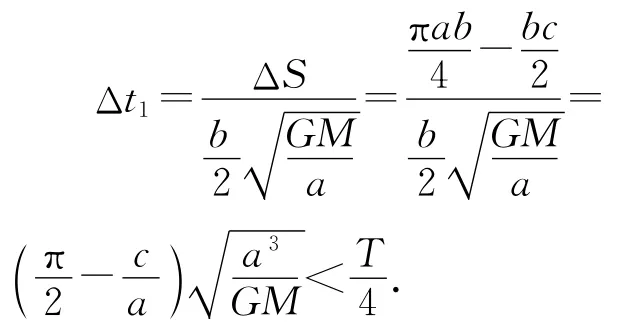
同理，可以推出由3位置到2位置所用的时间

由1位置到2位置所用的时间

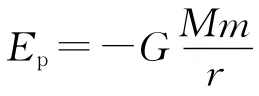
3 简谐运动中的时间问题

天体中简谐运动，在高考中不太常见，但是在强基计划的考试中经常出现，有两道经典例子如下.

例1.如图3，一小行星上有一个从表面A点到球心O的很窄的试验用、内壁光滑的矿井，行星表面A点处，无初速地掉入一物，则A掉到O点所经历时间是多少，已知行星半径为R，行星表面的重力加速度为g，行星质量均匀分布，不考虑行星自转.

图3

解析：应用知识点，质量分布均匀的球壳对壳内物体的引力为0.以O点为坐标原点建立竖直向上为正方向的x轴，物体处于位置x时，受到的地球引力，方向指向地球球心O点，大小为

例2.如图4，设想在地球表面A、B两地之间开凿一直通隧道，在A处释放一小球，小球在地球引力的作用下从静止开始在隧道内运动，忽略一切摩擦阻力.试求小球从A到B所需时间.已知地球半径为R，地球表面的重力加速度为g，地球质量均匀分布，不考虑地球自转.

图4