应用质点系质心动能定理法求解碰撞问题
2022-05-23徐华兵
徐华兵
(浙江省金华第一中学,浙江 金华 321015)
1 问题提出
笔者在给学生讲授动量、动量定理习题时碰到一道连续多个物体完全非弹性碰撞求解碰后速度问题,用牛顿运动定律和运动学公式法求解非常繁琐且复杂,而用质点系质心动能定理法求解却较为简单方便.
例1.在光滑水平面上的一条直线上,排列着一系列可视为质点、质量均为m的物体1、2、3、4,在1之前放着一个质量M=4m的物体A,相邻物体间的距离均为l,最初所有物体均静止,如图1所示.现用一水平力F推A,从而发生一系列完全非弹性碰撞.求:当运动物体与第4号物体相碰前的瞬间,其速度为多大?

图1
解析:物体A与物块1、2、3相继碰撞,碰撞过程中质量不断变化,物体的加速度不断变化.所以若用牛顿运动定律和运动学公式求解,必须对质点系与物体4碰前过程分子过程处理.
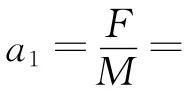

点评:本题是质点系质点完全非弹性碰撞问题,在碰撞过程中物体的质量不断变化,恒力F作用下加速度不断变化,用常规思路求解,必须分子过程处理,而且过程及其复杂.而此时若应用质点系质心动能定理法求解只需要找出力F作用前后质心位置,求出质心位移;算出质点系合外力对质心做的功,最后应用质心动能定理列式计算即可.
2 质点系质心动能定理表达式推导
质心是质点系统的质量分布中心,在给定的坐标框架下质心的位置矢量为
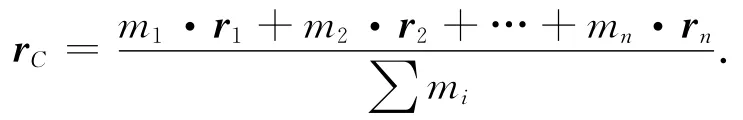
对时间t求导得
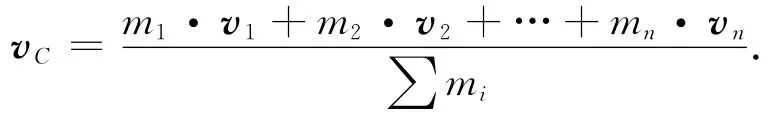
将速度v对时间t求导得

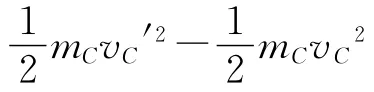
3 质点系质心动能定理求解碰撞问题分类剖析
根据质点系质点在运动过程中所受外力是恒力还是变力,可将质点系质点间的碰撞问题分为恒定合外力F作用下的碰撞问题和变合外力F作用下的碰撞问题.下面分上述两类情形剖析质点系质点间的碰撞问题.
3.1 质点系受恒定合外力F作用类碰撞问题
质点系受恒定合外力F作用类碰撞问题是指质点系内质点在整个运动过程中受恒定外力F作用的碰撞问题.但由于运动的质点不断增多,质量不断变大,虽是恒定合外力,运动质点的加速度却在不断变化,过程较为复杂;若采用质心动能定理求解碰撞后质点速度能简化运动过程,求解较为方便.
例2.一光滑杆上套3个质量为m的光滑圆环,相邻圆环间距都为l,如图2所示.现给环1施加一恒力F,环1在恒力F的作用下向着环2运动,环1和环2碰后在原来恒力F作用下一起向着环3运动.已知所有的碰撞为完全非弹性碰撞,求环1、2、3系统碰后的速度v3.
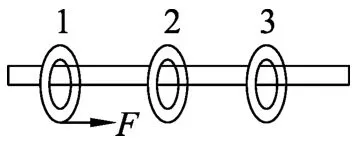
图2

变式1:一光滑杆上套n个质量为m的光滑圆环,相邻圆环间距都为l,如图3所示.现给环1施加一恒力F,环1在恒力F的作用下向着环2运动,环1和环2碰后在原来恒力F作用下一起向着环3运动,与环3碰后,环1、环2和环3在原恒力F的作用下向着环4运动,依次碰撞下去……已知所有的碰撞为完全非弹性碰撞.求与第n个环碰后系统的速度vn.
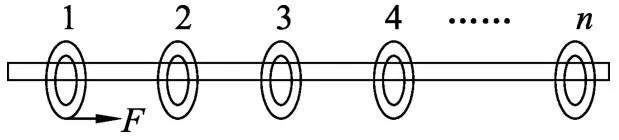
图3

点评:上述例2也可应用牛顿运动定律和运动学公式求解,且能快速求出,不是很繁琐;应用质点系质心动能定理求解的优越性还没完全表现出来.而变式1将质点系碰撞质点个数由3个拓展到n个,若用牛顿运动定律和运动学公式求解将会非常复杂,且运算量非常繁琐;而用质点系质心动能定理求解过程简洁明了清晰,优越性尽显.
3.2 质点系受变合外力F作用类碰撞问题
质点系受变合外力F作用类碰撞问题是指质点系内质点在整个运动过程中受变化合外力F作用的碰撞问题.由于运动质点系的合外力F不断变化,运动质点的加速度也在不断变化,从牛顿运动定律和运动学公式角度分析过程复杂;宜用质点系质心动能定理法求解.
例3.一粗糙杆上套3个质量为m的圆环,已知圆环与杆间的动摩擦因数为μ,相邻两圆环间距为l.现给环1一个初速度v0,使它向着环2运动,与环2碰后粘在一起,继续向环3运动,与环3发生碰撞,如图4所示.若环1、环2和环3间的碰撞都为完全非弹性碰撞,求:环1、环2和环3碰后粘合体的速度v3.

图4

变式2:一粗糙杆上套n个质量为m的圆环,已知圆环与杆间的动摩擦因数为μ,相邻两圆环间距为l.现给环1一个初速度v0,使它向着环2运动,与环2碰后粘在一起,继续向环3运动,与环3发生碰撞…直到与第n个环发生碰撞,如图5所示.若所有环间的碰撞都为完全非弹性碰撞,求与第n个环碰后粘合体的速度vn.
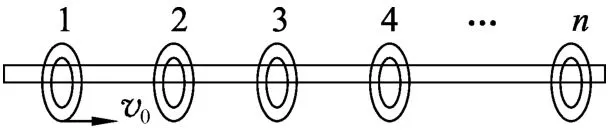
图5

点评:例3和变式2都属于受变化合外力F作用类质点系碰撞问题,若从牛顿运动定理和运动学公式角度求解质点系碰撞后的速度,过程较为复杂,难度较大;尤其是变式2中质点系从有限个较少的质点拓展到n个质点.此时,若用质点系质心动能定理法求解质点系内质点碰后速度,过程清晰明了简单.
质点系质点间完全非弹性碰撞问题在高中物理力学试题中常常出现,由于质点系研究对象多,碰撞过程复杂,这类试题从牛顿运动定律和运动学公式角度求解往往计算量大,且过程复杂,及其容易出错.本文为这类试题的求解提供了一种简单的方法——应用质心动能定理法求解质点系碰撞问题,希望对广大同行教师在讲授这类试题时有所帮助.
