物理实验探究过程中科学解释能力测评研究

李玉冰 丁格曼，2

（1.华南师范大学物理与电信工程学院，广东 广州 510006；2.华南师范大学物理学科基础课实验教学示范中心，广东 广州 510006）

哲学家基切尔和萨尔蒙曾说过：“为自然现象提供假设是科学探究的基本目的”.［1］随着时代发展，科学的本质从探究与实验逐渐改变为解释与论证.［2］这样的社会背景下，在《普通高中物理课程标准（2017年版）》中，科学解释被纳为物理学科核心素养中科学探究的一个重要组成要素.［3］由此可见，基于物理学科背景，评价并诊断学生的科学解释能力发展情况显得尤为重要.因此，本研究在Rasch模型的基础上，开发物理实验探究过程中的科学解释能力测评工具，并对测评工具进行质量检验，尝试测评高一学生在物理实验探究过程中的科学解释能力，并分析其特点.

1 高中生物理实验探究过程中科学解释能力测评框架

笔者初始分析国内外学者对科学解释、能力、实验探究的相关研究，［4-7］其中黄蕙欢［7］（2017）学者在科学解释CER框架的基础上界定了学生物理科学解释能力.本文沿用该框架，细化界定物理实验探究过程中的科学解释能力，即学生在物理实验探究过程中能利用已有的物理知识和从观察、实验或模型中获取的新证据、对问题或现象通过逻辑推理的方式进行判断、说明的能力，具体包括实验论断提出能力、证据提取能力、科学推理能力和辅助能力，如表1所示将其再进行细分.

表1 物理实验探究过程中的科学解释能力

此外，学生在实验探究过程中的科学解释能力是所界定的各部分能力彼此作用下的综合情况，不能简单地加减各部分能力.

在界定什么是科学解释能力后，要想测评学生在物理实验探究过程中的科学解释能力，还需要对该能力进行水平划分.考虑到SOLO分类理论具有较强的可操作性，［8］并且可以将质性评价与量性评价相结合，［9］本文结合SOLO分类理论以及《普通高中物理课程标准（2017版）》中学业质量水平部分关于科学解释的划分，考虑到抽象拓展水平有时候连专家都不一定可以达到，故将科学解释能力划分成4个水平，具体如表2所示.

表2 物理实验探究过程中的科学解释能力水平划分

2 高中生物理实验探究过程中科学解释能力测评工具的开发

2.1 开发过程

物理实验探究过程中的科学解释能力是一种内隐的、从后天习得的能力类型.该能力可以依据学生回答问题的思维方式进行测量与评价.在比较访谈法、问卷调查法、纸笔测试法等常见且行之有效的测量方法后，考虑到纸笔测试法容易获取大量数据，并且与学生的适配性较强，测试时学生容易发挥出正常、真实的水平，因此本研究采用纸笔测试法对学生在实验探究过程中的科学解释能力进行测评.题目类型选择开放式问题和封闭式问题相结合.

而为保证所开发的测量工具具有较好的信效度，本文选择项目反应理论作为理论支撑，其基本思想是展现被测试的对象在各个试题上的回答情况与其内在的某种品质之间的关系，其项目特征曲线就是用来表示这种关系的.［10］如图1项目特征曲线所示，其显示具有θ能力的被试者答对某个项目的概率为P.利用该理论建立起具有固定不变的参数的测评项目，统一对比不同的测验量表分数.

图1 IRT理论的项目特征曲线

上文已经划分了学生在实验探究过程中的科学解释能力水平层次，而科学解释在实验探究过程中主要体现在对实验进行假设、分析实验数据、解释实验现象和形成实验结论等环节上.故本研究围绕科学地解释实验情况、对实验中的变化情景做出解释性假设、分析实验证据和总结实验结论、论证和辩护自己的实验观点，通过举例、使用图像或模型等方法辅助说明实验问题等内容进行试题命制.

根据测评内容和要求命制试题后，邀请物理教学研究者和部分骨干教师对试题提出修改意见，并邀请部分学生进行试做后提出答题体验，结合两者的意见对试题进行修改后试测.统计试测结果后运用 Winsteps软件进行数据分析，基于Rasch模型检验试题的信度、效度、区分度以及数据—模型拟合参数等，对不符合要求的试题进行修正后再进行实测.

2.2 质量评估

本文在试测对象上选择高一年级中选修物理科目的A班、B班两个班级的学生，其中A班为重点班，B班为平行班，该群体学生的物理成绩跨越30分到100分，具有较好的代表性.本轮共发放120份试题，回收的有效试卷为70份，试卷的有效回收率为68%.根据各个题目的评分标准，对学生的回答进行赋分，从而得到本研究的数据.

由于本测评工具具有较多的开放性试题，为保证评分者赋分的可靠性，本文运用Kendall's W（肯德尔和谐系数）考查评分者评分的一致性.在评分过程中随机抽取10份试卷，利用SPSS数据处理软件统计3位评分者间的肯德尔和谐系数为0.893，渐近显著性系数为0.004，说明此份试题的评分标准比较公平公正，受主观因素影响较小（表3）.

表3 初测评分者信度统计表

在此基础上，将所得到的数据输入Winsteps软件，检测所编制的测评工具是否符合Rasch模型.结果表明，该测评工具的整体信度为0.97，分离度为5.70（正常需要大于2），总体的数据—模型拟合参数MNSQ接近1、ZSTD接近0，说明该试题的信度比较理想，同时分离度也较好，符合Rasch模型的要求，可进一步进行分析.而从单维性检验上看，试题的总体单维性较好，但有4道试题不符合单维性要求，需要进行调整.而对各道试题进行单独分析发现，只有项目7的数据与模型不拟合，说明有部分能力水平低的测试对象回答正确，部分能力较好的测试对象却在此题上回答错误.

3 高中生物理实验探究过程中科学解释能力表现的测评分析

实测选择了广州市某高中高一年级的5个物理班级，其中2个为重点班，3个为平行班.本次共回收130份测评试题，有效份数为112份，有效回收率为86.2%，其中男生样本57份，女生样本55份.首先，再次检验该试题的有效性和可靠性，其中利用SPSS计算其评分者信度为0.952，渐近显著性系数为0.002，符合要求.而利用Winsteps软件计算其信度为0.98，区分度为6.52，除项目9和项目1的非加权标准差均方略超出-2到2的可接受区间外，其余均符合Rasch模型的使用要求.然后继续检验单维性、项目—被试反应、点—测相关系数、模拟标准误差均大致满足Rasch模型的使用要求，适合用此模型进行后续分析.

3.1 样本学生总体表现水平

Rasch模型可以通过将原始分转换为logit得分，将被试能力、项目难度放在同一把量尺上进行比较.表4是实测学生科学解释能力分布情况的统计数据，样本学生的最高logit得分和最低logit得分相差3.14，说明测试对象具有较广的科学解释能力水平分布；而标准差为0.64，说明测试对象的科学解释能力水平存在较为显著的差异.如图2，依据学生的logit得分绘制各个分数的频率分布直方图，可以发现所测对象的科学解释能力整体呈正态分布.

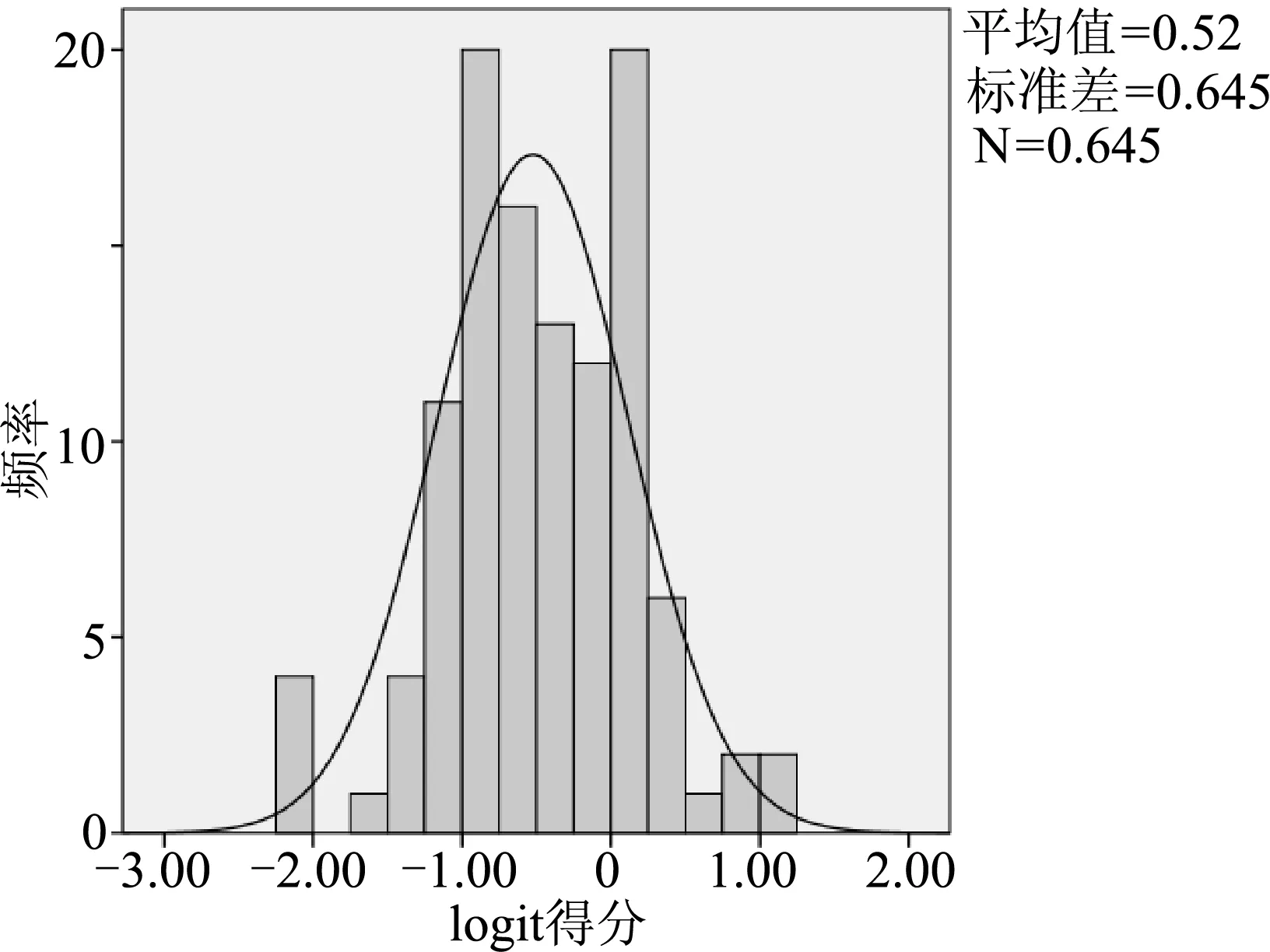
图2 学生logit得分的频率分布直方图

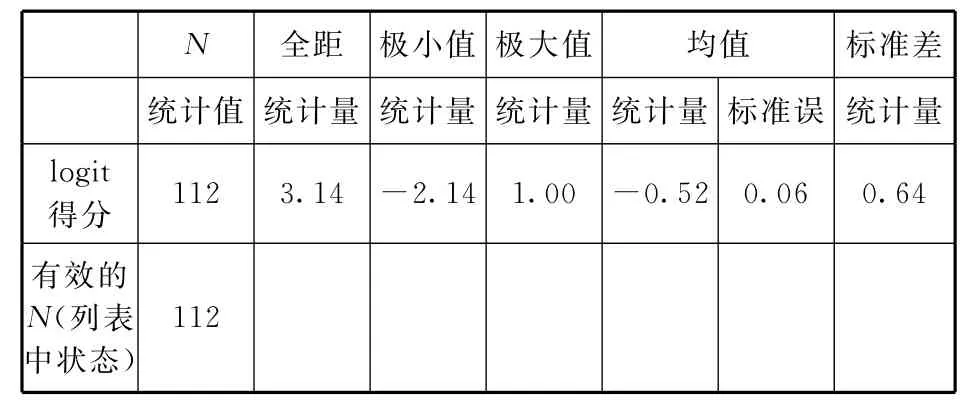
表4 学生logit得分的描述性统计

另外，本研究根据整体怀特图来划分样本学生在实验探究过程中的科学解释能力，划定的水平分界值具体如下：处于水平4的学生应该是大部分项目得3分的，logit≥1；处于水平3的学生应该大部分项目得2分，-0.67≤logit＜1；处于水平2的学生应该是大部分项目得1分的，-1.88≤logit＜-0.67；处于水平1的学生，logit＜-1.88.

根据划定的能力值范围，统计样本学生数，得到学生在各个能力水平上的百分比如图3所示.由图可发现，学生的科学解释能力水平集中在水平2和水平3，占总人数的94.64%.

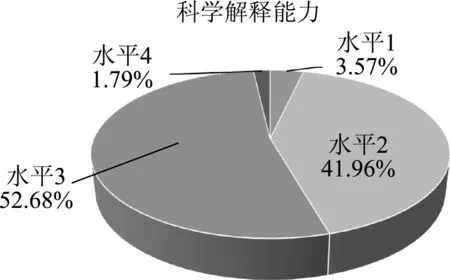
图3 学生实验探究过程中的科学解释能力水平分布情况

3.2 样本学生科学解释能力与物理成绩的相关性分析

将所测学生的科学解释能力得分和其物理成绩进行相关分析，运用学生高一上学期期末考试的物理成绩作为本次物理成绩的衡量标准，该阶段学生已经具备此份科学解释能力测评试题所需的全部知识，且高一上学期期末考试学生相对比较重视，故用此份成绩作为学生的物理成绩进行分析.

根据图4的散点图可以大致看出学生在实验探究过程中的科学解释能力与物理成绩之间存在线性相关关系.在此基础上进行科学解释能力和物理成绩间的双变量相关分析.表5、表6为皮尔逊相关的分析结果.

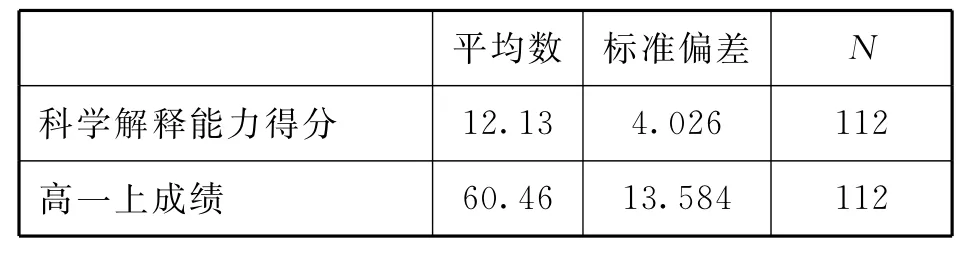
表5 描述性统计资料

表6 相关性统计数据

续表

图4 科学解释能力得分与物理成绩的相关散点图

从表中可以看出，学生物理成绩平均分为60.46，能力测评平均分为12.13，双变量相关性检验得到的皮尔逊相关系数为0.475，在0.01水平上显著相关，说明学生在实验探究过程中的科学解释能力与学生的物理成绩具有正相关性，平时物理成绩较好的学生在实验探究过程中的科学解释能力也比较好.这是因为进行科学解释其实是需要一定的科学知识作为依托的，但两者间的相关性系数小于0.5，说明并不具备强烈相关性，也就是并不是平时物理成绩好的学生就一定具备良好的科学解释能力.

3.3 不同性别学生科学解释能力的比较分析

将男生和女生的科学解释能力进行独立样本T检验，看看两者之间是否存在显著性差异.

从表7中数据上看，男生的科学解释能力平均值为12.44分，女生的科学解释能力平均值为11.82分，男生的能力均值比女生高0.62分，说明男生的表现比女生稍微要好.但从方差齐次检验结果显示，如表8中数据，对于学生的能力水平，其F值为0.942，显著性概率为0.334，大于显著性水平0.05，符合方差齐次.而均值方程的t检验结果显示，双侧显著性概率为0.417，大于0.05，说明男生和女生之间在实验探究过程中的科学解释能力无显著性差异.

表7 不同性别学生实验探究过程中科学解释能力的描述性统计

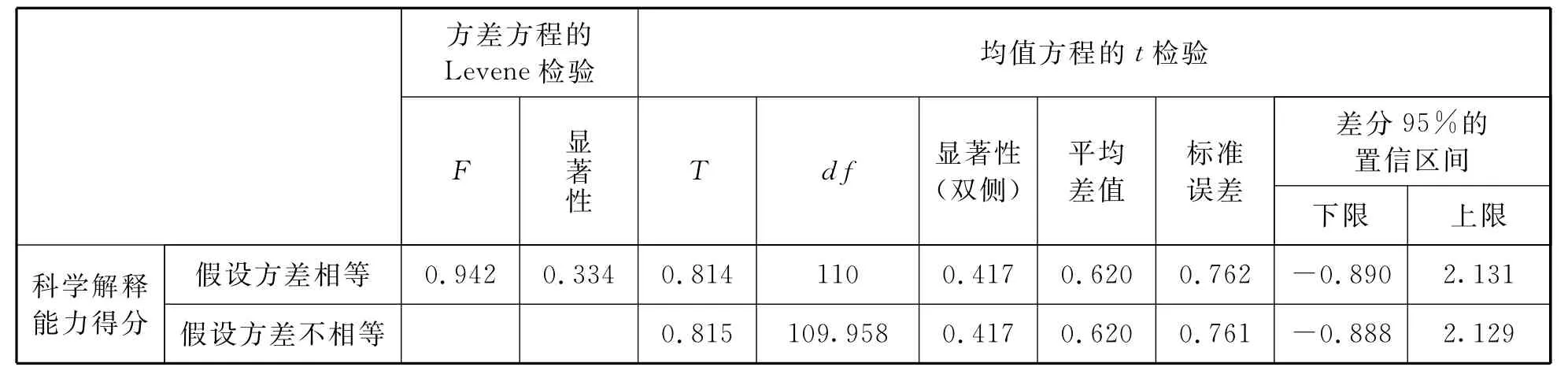
表8 独立样本T检验

4 高中生科学解释能力培养现状

考虑到物理课堂是学生实验探究过程中的科学解释能力的主要培养阵地，本研究设计了针对教师的科学解释能力培养调查问卷.该问卷涉及对科学解释的认识和科学解释的培养现状两方面的内容，经过一周的网络问卷发放后，共回收81份有效问卷，其中教龄10年以上的教师占69.51%，35.37%的调查对象是高级教师，40.24%的调查对象是中学一级教师.他们多是教学经验丰富的教师，对中学物理教学较为熟悉.

将调查结果回收统计发现，高达91.36%的教师认为在实验探究过程中很需要科学解释能力，肯定了培养学生科学解释能力的重要性，但实际上仍有54.32%的教师对科学解释了解甚少.而在培养现状上，61.73%的教师认为自己在日常教学中会较为注重学生科学解释能力的发展，但仍会因考学压力、课时紧张、系统性理论指导的匮乏以及没有具体的实施方案等多种影响因素，无法顺利培养学生的科学解释能力.

5 测评结果讨论与教学建议

本文以测评学生在物理实验探究过程中的科学解释能力为目标，构建测评框架并开发相应的测评工具，通过检验发现设计的测评工具符合Rasch模型的相关质量指标，具有可信度.而分析被试在实测过程中的科学解释能力表现可发现，总体来看被试在实验探究过程中的科学解释能力得分呈正态分布，绝大多数学生都处于水平2和水平3，并且其能力与物理成绩具有正相关性，但并不是强烈相关.虽然男生被试在实验探究过程中的科学解释能力测试得分略高于女生被试，但不同性别的被试在实验探究过程中的科学解释能力无显著性差异.而从被试的答题情况上分析发现具有3点不足：一是被试在解释过程中依赖于定性分析，定量解释上欠缺明显；二是部分学生在科学解释过程中难以抓住关键研究量，避开干扰量；三是部分学生在尝试解释过程中存在证据与推理混乱的现象，无法准确获取证据信息并运用其进行推理解释.

科学解释能力作为物理核心素养中的重要组成部分，将会影响学生的未来成长以及对复杂问题的应对情况.而物理课堂是学生实验探究过程中的科学解释能力的主要培养阵地，在剖析教师调查数据后可察觉，部分教师不太了解科学解释，自身对于科学解释的知识储备也不足，虽能意识到科学解释的重要性但缺乏实践，因此提出以下建议.

（1）吸纳相关知识，联动互补共建.

培养学生的科学解释能力首先需要教师具备充足的科学解释知识，笔者认为可以从教师的继续教育出发：一方面是可以利用线上、线下等多种形式进行科学解释的相关研讨，疫情期间各大线上会议软件的频繁使用，无疑也给现阶段的教学研讨提供新的方式，通过组织线上的分享会、研讨会联系教师们进行科学解释材料的相关分享与研读；线下则可以参与各地的名师工作室、教师培养计划等，从中汲取相关知识，使科学解释培养有法可施、有路可循；另一方面是教育主管部门或学校可以适当召开关于科学解释培养、核心素养解读的相关教育培训，有意识地为提高学生的科学解释能力出谋划策，落实立德树人的培养目标.

（2）显化科学解释，营造解释氛围.

要想培养学生的科学解释能力，最先要在课堂上显化科学解释，让学生知道科学解释包括论断、证据、推理等三要素，并且要尝试运用教学语言为学生们示范如何进行科学解释，引导学生在之后的实验探究环节中如何形成有依据的论断、如何获取证据、如何从证据中总结规律、如何基于有效的逻辑推理解释实验现象或结论等，在实验探究的过程中落到实处、强化培养学生的科学解释能力.此外，在教学中，教师可以适当改变以往传统的命题方式，创设情景设计结构不良试题，引导学生在解决真实物理问题的过程中锻炼科学解释.