基于共形阵的角度和极化信息联合估计算法
2022-05-23曲志昱戴幻尧
曲志昱, 孙 萌,*, 戴幻尧
(1. 哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001; 2. 先进船舶通信与信息技术工业和信息化部重点实验室, 黑龙江 哈尔滨 150001; 3. 中国洛阳电子装备试验中心, 河南 洛阳 471003)
0 引 言
共形阵列是将天线单元共形贴附于载体表面而构成的天线阵列。一般来说,共形阵列具有安装简单、节省空间、空气阻力小和波束扫描范围广等优点,在星载、机载、弹载及通信领域有着广泛的应用前景[1-3]。但由于载体曲率的影响,各个天线单元方向图指向不一致,从而呈现出多极化特性[4],同时载体的遮挡效应会使得一部分天线单元接收信号幅度下降或无法正常接收来波信号,从而导致测向算法性能急剧恶化。
针对这一问题,国内外学者开展了广泛研究并取得了一定的研究成果[5-18]。文献[5]针对各个天线单元向图指向差异的问题进行研究,采用三次欧拉旋转变换实现了局部坐标系和全局坐标系的转换,为共形阵列的波达方向(direction of arrival, DOA)估计奠定了基础;文献[6]将经典多重信号分类(multiple signal classification, MUSIC)算法移植到共形阵列天线中,推导了MUSIC算法在共形阵列中的估计性能;文献[7-8]针对锥面共形阵列分别采用降维搜索MUSIC算法和四维搜索MUSIC算法实现了DOA和极化参数的联合搜索;文献[9-10]针对锥面和柱面共形阵列,先将DOA参数和极化参数去耦合,然后采用旋转不变子空间(estimation of signal parameters via rotational invariance techniques, ESPRIT)算法的思想实现了DOA和极化参数的联合估计;文献[11-12]针对圆柱共形阵列采用插值的方式,将原有阵列转换为虚拟嵌套阵列,然后分别采用ESPRIT算法和总体最小二乘(total least square, TLS)-ESPRIT算法实现了DOA参数的估计;文献[13-14]引用四元数概念,采用四元数降维MUSIC算法依次估计出来波信号的DOA参数和极化参数,实现多参数联合估计;文献[15-16]采用插值技术实现嵌套虚拟阵列,并采用MUSIC算法实现了来波信号的DOA参数估计;文献[17]采用子阵分割和插值的方法解决了共形阵列的遮挡效应,并采用ESPRIT算法实现了DOA参数的估计;文献[18]利用张量结构,采用基于变化域张量的MUSIC算法实现了DOA和极化参数的联合估计。
现有参数估计算法主要考虑从理论模型计算理论导向矢量,结合测向算法进行DOA和极化参数的联合估计,在实际工程应用中可能会出现估计精度较低,甚至无法应用的情况。为此,本文从另一种角度考虑此类问题,利用天线实测方向图数据重构导向矢量,天线阵元的实测方向图数据中包含了各个天线阵元的空间位置信息以及极化指向角信息,同时天线方向图是在综合了幅相误差、耦合误差、位置偏差等各种误差之后得到的数据,所以有理由利用天线的方向图数据重构阵列的导向矢量,最后结合测向算法完成参数估计。
由于没有实测的方向图数据,所以本文首先利用三维电磁场仿真软件CST (Computer Simulation Technology)对共形天线阵列进行仿真获取方向图数据,用以模拟真实的方向图数据,然后以此为基础重构空域相位—极化敏感矩阵,进而得到重构的导向矢量矩阵,最后结合极化MUSIC算法[19]进行多参数联合估计。由于本文改进算法中的导向矢量是方向图矩阵通过分解重构的方式获取的,因此相对于理论的导向矢量计算,本文改进算法明显具有更低的运算量。通过蒙特卡罗仿真实验验证了本文改进算法的有效性和优越性。
1 共形天线结构及数学模型
考虑由N=8个偶极子天线构成的均匀圆环共形阵列,贴附于半径为r的圆柱表面,如图1和图2所示。
在直角坐标系下各个阵元的坐标为(xi,yi,zi),i∈(1,2,…,N)。假设在某个t时刻有M(M X(t)=AS(t)+N(t) (1) 式中:X(t)=[x1(t),x2(t),…,xN(t)]T为N×K维阵列接收数据矢量;S(t)为M×K维的信号矩阵;N(t)为N×K维的加性高斯白噪声矩阵。 A=[a(θ1,φ1,η1,γ1),a(θ2,φ2,η2,γ2),…,a(θm,φm,ηm,γm),…,a(θM,φM,ηM,γM)] 式中:A为N×M维的阵列流型矢量,即联合导向矢量;γm为第m个信号的极化辅助角(0≤γ≤π/2);ηm为第m个信号的极化相位差(-π<η≤π),第m个信号的导向矢量为 (2) (3) (4) 式中:h(ηm,γm)为第m个信号的极化矢量,它只与信号的极化状态有关;Φ(θm,φm)为将第m个信号的极化矢量从球坐标系转换为直角坐标系下的坐标变换矩阵,只与入射信号的方位角和仰角相关。 βn为该天线单元的垂直指向角,定义如图3所示。 (5) 理论上讲,电场可以在任意一对正交极化基上分解,其中应用比较广泛的一种分解方法为球坐标系分解法,如图4所示。 (6) (7) 则天线单元对来波信号的响应E可由下式表示: (8) (9) (10) (11) 将式(11)代入式(9)可得 (12) 利用阵列输出矢量X(t)的K次独立快拍计算样本协方差矩阵: (13) 对矩阵Rxx进行特征分解,可以得到 (14) 式中:US为大特征值对应的特征矢量所张成的子空间,即信号子空间;UN为较小特征值对应的特征矢量所张成的噪声子空间。理想情况下信号子空间与噪声子空间相互正交,即信号子空间中的导向矢量与噪声子空间也相互正交: (15) (16) (17) 将其代入式(16)可得: (18) (19) (20) 式(20)左乘非零矩阵Dcg(θm,φm)HUN,得到 (21) 所以有下式成立: (22) (23) 根据上述公式推导计算可知,在无噪理想条件下,H(θ,φ)矩阵在真实的M个信号DOA处发生秩亏损现象,由满秩变为奇异矩阵,即H(θm,φm)(m=1,2,…,M)为奇异的Hermite矩阵;而Dcg(θm,φm)HDcg(θm,φm)为Hermite正定矩阵,所以{H(θm,φm),Dcg(θm,φm)HDcg(θm,φm)}矩阵束的最小广义特征值为0。由式(22)可知H(θm,φm)h(γm,ηm)=0,所以h(γm,ηm)与{H(θm,φm),Dcg(θm,φm)HDcg(θm,φm)}的零广义特征值对应的广义特征向量满足比例关系,即 (24) 由信号极化辅助角γ和极化相位差η的定义可以得到极化参数的计算公式: (25) (26) 步骤 1利用共形阵列获取信号矩阵X(t)并计算相应的协方差矩阵: Rxx=E[X(t)XH(t)] (27) 步骤 2对协方差矩阵Rxx进行特征分解,获取N-M个较小特征值对应的特征矢量,作为噪声子空间UN(其中M已知或已准确估计)。 步骤 4根据得到的噪声子空间UN和空域导向矢量Dcg(θ,φ)构造谱函数PMUSIC,根据式(23)在全空域范围内谱峰搜索获得来波信号的方位角和仰角。 步骤 5将来波信号的入射角度信息带入H(θm,φm)和Dcg(θm,φm)HDcg(θm,φm)中,组成矩阵束{H(θm,φm),Dcg(θm,φm)HDcg(θm,φm)}。 步骤 6对上述矩阵束特征分解获取最小特征值对应的广义特征矢量,再根据式(25)和式(26)获得来波信号的极化参数。 本节通过仿真实验对所提方法进行验证,然后与经典极化MUSIC算法[19]进行对比。采用如图1所示的圆环共形阵列,半径r=100 mm,阵元个数为8,且均匀分布在圆柱表面,偶极子天线平行于水平面放置,窄带远场信号的入射频率为2.5 GHz。 (1) 使用CST软件仿真图1所示的共形阵列方向。仿真结果包括各个天线单元总幅度方向图、方位分量幅度方向图、方位分量相位方向图、俯仰分量幅度方向图、俯仰分量相位方向图,天线1总幅度方向图如图5所示。 由图5仿真的方向图结果可以看出,天线单元对未遮挡的来波信号的幅度响应明显强于遮挡方向来波信号的幅度响应,整体与理想方向图数据十分接近,因此可用该仿真方向图数据模拟真实方向图数据。 (2) 验证方法有效性。设有两个频率为2.5 GHz的窄带远场信号,参数分别为 [θ1,φ1,γ1,η1]=[265°,53°,54°,21°] 噪声为零均值加性高斯白噪声,信噪比为13 dB,快拍数为128。基于重构的导向矢量,结合改进极化MUSIC算法进行空域—极化域联合估计仿真,结果如图6和图7所示。 图6是通过式(23)在角度域(φ,θ)内二维搜索得到的谱图;图7是在DOA参数得到之后利用式(19)在极化域(γ,η)内二维搜索得到的结果,四个参数的搜索步长均为0.2°。由仿真结果可以看出,本文所提的方法可以十分准确地估计出来波信号的DOA与极化参数,验证了该算法的有效性。 (3) 仿真分析算法性能,包括算法对信源的成功分辨率分析和参数估计误差分析。仿真条件与仿真实验2的条件一致,信噪比从10 dB逐步增加到35 dB,步进5 dB,每个信噪比下进行500次蒙特卡罗实验。当所有的参数(θ,φ,γ,η)估计值与入射信号的真值均相差2°以内时,定义此次测向成功,总成功分辨率为总成功分辨次数与总仿真次数之比,仿真结果如图8所示。 参数估计误差分析包括DOA参数的均方根误差分析与极化参数的均方根误差分析,定义入射信号的二维DOA参数均方根误差为 (28) 同理入射信号的二维极化参数均方根误差为 (29) 式中:k∈{1,2,…,500}为蒙特卡罗实验次数。参数估计误差随信噪比变化曲线图如图9~图12所示。 由上述误差曲线图可以看出,随着信噪比的增加,所有算法的参数估计成功概率均逐步增加;在较低信噪比下,相对于其他的方法,本文算法估计成功分辨概率更高,参数估计均方根误差更小。根据仿真结果可知,本文算法具有更高的估计性能。 本文针对共形天线阵列固有的遮挡效应和多极化特性,提出一种用天线方向图矩阵重构导向矢量的方法,并基于此提出改进极化MUSIC算法,实现了对来波信号DOA和极化参数的联合估计,且无需考虑参数配对问题。相比于经典极化MUSIC算法,本文所提方法具有更高的估计精度和分辨率,同时由于本文导向矢量的计算采用方向图矩阵重构的方式实现,因此避免了理论导向矢量计算中的较大计算量。计算机仿真实验验证了算法的性能,并可应用至任意形状的共形天线阵列。若采用实测天线方向图数据,本文方法可以推广至实际工程应用中。
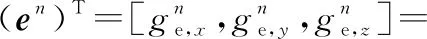


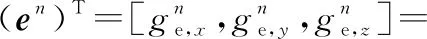


2 多参数联合估计算法原理

2.1 导向矢量重构





2.2 方位角及仰角估计






2.3 极化参数估计

2.4 算法步骤

3 仿真实验及性能分析
[θ2,φ2,γ2,η2]=[165°,63°,60°,48°]4 结 论
