基于低轨星网的多目标协同跟踪滤波技术

翟 光, 王妍欣, 孙一勇

(北京理工大学宇航学院, 北京 100081)

0 引 言

星网探测系统将天基观测器和光学传感器相结合,以其覆盖范围广、精度高、传感距离远而受到广泛的关注。与单颗卫星相比,星网能够整合整个卫星星座采集的数据,实现目标的连续跟踪[1-2]。由于卫星探测范围内可能存在多个目标以及光学传感器的各种不确定性,因此根据量测值无法直接反推目标的位置[3]。一旦将错误的测量值分配给目标,会对估计结果产生巨大影响。当目标进行机动时,目标的动力学模型随即改变,增加了多目标协同跟踪的难度。因此,研究一种针对低轨星网的多目标跟踪算法具有重要意义。

基于低轨星网的多目标的跟踪问题可以分为数据关联阶段和多目标状态更新阶段。数据关联技术是状态估计问题的前提,在多目标协同跟踪中起着重要作用[4]。多目标数据关联技术旨在建立目标与量测值之间的映射关系,并实现对量测值的分配。最近邻数据关联(nearest neighbor data association, NNDA)算法是最著名的数据关联算法之一,其通过比较目标预测位置和测量值之间的距离来区分目标的相关测量和杂波干扰。除了最近邻思想,还有一种基于概率分析的数据关联思想,如概率数据关联(probabilistic data association, PDA)[5]解决了杂波背景下简单目标的数据关联问题。在PDA算法的激励下,相关学者又提出了联合PDA(joint PDA, JPDA)[6]和多假设跟踪(multiple hypothesis tracking, MHT)[7]实现多目标的数据关联。JPDA算法考虑了多个量测来源于其他目标可能性,但算法所需的计算量呈指数级增长[8]。MHT算法被证明是一种适用于多目标跟踪的贝叶斯最优算法,但其精确解的计算存在困难[9]。为了减少计算量,又开发了廉价JPDA(cheap JPDA, CJPDA)[10]、次优JPDA (suboptimal JPDA, SJPDA)[11]和多帧分配(multiple frame assignment, MFA)[12]算法。然而,大部分数据关联算法都是根据对目标的三维量测信息进行关联,根据光学传感器平面的二维量测信息即目标的方位角进行多目标数据关联的算法很少。由于任意两个不关联的角度轨迹都可能产生幻影目标,因此必须确定测量值的来源,将来源于同一目标的量测值进行关联。为解决这一问题,文献[13]提出最小距离偏差算法,文献[14]提出二面倾角算法。然而这些算法都利用了几何约束,无法实现时间维度上的数据关联。因此,有必要开发一种数据关联算法,从空间和时间两个维度解决数据关联问题。

状态更新阶段即是根据测量值的关联结果估计多个目标的状态。卡尔曼滤波(Kalman filter, KF)是一种应用最广泛的状态估计算法[15]。虽然KF已被证明在高斯白噪声假设下能获得线性离散系统在方差最小意义下的最优估计[16],但由于低轨星网和目标的动态特性,KF不适用于多目标跟踪。为了将KF扩展到非线性系统中,学者们进行了大量的研究。在现有的非线性滤波器中,扩展KF(extended KF, EKF)因其实现简单、计算量小而得到广泛应用,由于EKF采用二阶泰勒展开对非线性系统进行近似,忽略了高阶项,因此只适用于弱非线性系统。为了更精确地逼近非线性系统,文献[17-18]采用基于无迹变换的无迹KF(unscented KF, UKF)来解决多目标跟踪问题。综合考虑对非线性系统的逼近精度和计算量之间的平衡,本文采用基于UKF的状态更新方法。然而,目标的机动序列对跟踪系统未知会使得滤波器的性能显著下降[19-20]。一般来说,由目标机动引起的滤波发散问题可以通过膨胀协方差以增加新测量值权重的方法解决[20-21]。但这种方法只适用于脉冲式机动。文献[22-23]提出了一种基于协方差膨胀的衰减记忆滤波器来解决机动目标跟踪(maneuvering target tracking, MTT)问题。这两种算法的思想都是增加测量值的权重,但其代价是跟踪精度的降低。文献[24-25]通过将未知机动增广到估计状态,提出了增广KF(augmented KF, AFK)。但由于状态维度的增加带来了更大的计算量。为解决这个问题,学者们提出了变结构滤波算法[26],利用KF和AKF,既能保持机动目标的跟踪精度,又能提供较好的非机动目标跟踪性能。在变结构方法的推动下,多种算法得到发展,如变状态维度(variable state dimension, VSD)算法[27],增强VSD(enhanced VSD, EVSD)算法[28]等。与单滤波器相比,交互式多模型算法[29-30]则是对多个单独模型跟踪的估计值进行加权求和,得到组合状态估计,但同时运行多个滤波器必然增加了计算量,特别是对于非机动目标,不仅不会提高跟踪性能,反而会降低定位精度。

本文针对低轨星网只能获得目标方位角信息的测量特性,通过设计指标函数来确定测量值的分配,将三维关联转化为测量平面关联,有效地实现多目标的数据关联;并将状态更新与数据关联算法相结合,建立了多机动目标跟踪算法的总体框架。通过机动检测函数确定机动的开始和结束,从而完成状态估计器在标准UKF和增广UKF(augmented UKF, AUKF)之间的切换。最后通过仿真试验对算法的可行性与有效性进行验证。

1 数学模型

1.1 目标弹道动力学模型

导弹离开大气层后,进入自由飞行段,在不考虑空气动力学和地球自转的情况下,目标运动仅受到重力和发动机推力的影响。考虑带有推进器的多个目标,取目标j(j=1,2,…,Nt)在地心惯性坐标系下的位置[x,y,z]T和速度[vx,vy,vz]T为状态向量,即

X(j)=[x,y,z,vx,vy,vz]T,j=1,2,…,Nt

(1)

式中:Nt为t时刻目标总个数。多目标在地心惯性坐标系下的动力学模型可以描述为

(2)

式中:μ0=3.986×105km3/s2为地心引力常数;W(j)(t)表示目标的系统噪声,其方差阵为Q(j)。

1.2 弹道目标天基观测模型

低轨星网的卫星以一定的构型在空间分布,其中Walker星座是一种常用的圆形轨道星座,星座内卫星的轨道具有相同的高度、倾角和偏心率,其星座构型可用N/P/f描述,其中N为卫星总个数,P为卫星分布的轨道面数,f为相邻轨道面卫星相对相位因子。设星座中某颗卫星编号为m,则卫星m的升交点赤经和近地点角距可以表示为

(3)

对于配备光学传感器的卫星,当目标进入卫星的探测范围,如图1所示,就可以获取目标的方位角信息。对于目标j,若满足如下条件则可被卫星i探测到:

(4)

式中:α(i)表示卫星i的半视场角;η(ij)表示卫星i和目标j之间的夹角;ST表示由卫星至目标的位置矢量;OS表示地心至卫星位置矢量。根据余弦定理,式(4)可以写为

(5)

(6)

式中:[xs,ys,zs]T表示卫星在地心惯性坐标系中的位置向量。

若卫星和目标满足式(5)和式(6),则表示目标处于卫星的探测范围。对于携带光学传感器的卫星,可以得到目标在星固坐标系下的方位角和俯仰角,根据目标j和卫星i在地心惯性坐标系中的状态矢量,可以得到目标在地心惯性坐标系下的量测方程:

(7)

从量测方程中也可以看出,量测值中包含卫星的位置信息,因此利用量测信息得到的目标状态估计值必然与卫星自身定轨精度相关。为了在低轨星网的观测条件下实现多目标的协同跟踪,除了卫星星座的定轨精度,还必须保证各卫星时间基准和空间基准的统一,只有在统一时空架构下获取的观测信息才能用于多目标的数据关联及状态更新。因此,本文提出如下假设。

(1) 卫星配备完善的自主导航体系,能够满足在星座构型保持及重构过程中的自主定位。因此在本文中认为卫星的导航精度很高,卫星自身的导航误差不足以影响对目标的跟踪精度。

(2) 用于多目标跟踪的低轨星座经过准确的时空对准,且网络传输无延迟,即用于协同跟踪的量测值都是同一时刻获得的,且无延迟地传送到处理中心。

2 多目标协同跟踪滤波

2.1 基于卡方分布的数据关联

本文的目的是设计一种针对低轨星网的多目标协同跟踪滤波算法。由于根据单颗卫星获得的目标方位角无法反推目标的三维位置信息,使得针对三维轨迹的数据关联算法失效。实现对多目标的状态估计的前提是明确不同量测值的来源,即量测值的数据关联。低轨星网的多星对多目标观测关系随时间变化情况如图2所示。从图2中可以看出,要实现多目标的协同跟踪,一方面需要根据量测的来源将当前时刻的量测进行分组;另一方面,需要建立当前被检测目标与历史目标之间的映射,以绘制完整的轨迹。

(8)

定义一个目标被一颗卫星观测到一次为一组量测,则星座对多目标的量测组数为

(9)

为了根据这Ntrk组量测得到多目标的三维轨迹,对NNDA算法进行改进,利用变结构框架实现多目标的数据关联和状态估计。

由于光学传感器只能得到目标的方位角信息,本文构建虚拟的量测跟踪门,并利用卡方分布对量测数据进行分配,以实现测量平面的数据关联。基于卡方分布的数据关联算法主要包括如下步骤。

(10)

(11)

(12)

式中:h为选定的时间步长。

进一步得到状态的一步预测值为

(13)

(14)

(15)

(16)

(17)

(18)

式中:Assi表示卫星i观测到的量测与已有目标的数据关联结果。

2.2 信息融合与多目标状态更新

由第2.1节设计的数据关联指标函数可以实现量测量的分配,进而可以通过KF算法对多星的测量结果进行数据融合从而实现多目标状态更新。但是由于目标机动存在不确定性,若不考虑目标机动会导致目标状态方程的不准确,进而导致滤波精度降低。AKF被广泛用于未知机动推力恒定的目标状态估计。然而,由于AKF增加了系统状态,其实时性不如标准KF。本文跟踪的目标是弹道导弹的自由飞行段,目标受力特性较为简单,仅受重力和发动机推力的影响,不需要考虑空气动力,因此目标机动的原因只有发动机的推力,可以较为准确地建立以目标动力学模型为基础的状态方程。针对标准KF和AKF的切换问题,提出了变结构估计(variable structure estimation, VSE)。在VSE的激励下,本文开发了一种可变结构UKF(variable structure UKF, VSUKF)来自适应地估计未知机动。在VSUKF框架内,如果检测到机动,滤波器结构将切换为AUKF,即

(19)

当机动结束时,则利用UKF估计目标的状态,即

(20)

为了根据量测分配矩阵得到目标的量测矩阵,定义如下算法函数:

C=Meas(A,B)

(21)

cj=aA(i)bA(i),i=1,2,…,n;j=1,2,…,rank(A)

(22)

式中:A(i)=diag(a1,a2,…,ai)为矩阵A的分块矩阵;A(i)=rank(A(i))为矩阵A(i)的秩。

由此,目标k的量测矩阵可以表示为

(23)

式中:I1×2=[1,1]表示1×2维的矩阵，且矩阵元素全部为1。

与量测值对应的卫星位置矩阵可以表示为

(24)

根据数据关联的结果,目标k的状态估计值为

(25)

(26)

(27)

计算量测值采样点:

(28)

(29)

计算滤波增益矩阵:

(30)

将式(23)和式(30)代入式(25)可以得到

(31)

均方误差阵更新:

(32)

(33)

(34)

(35)

(36)

2.3 变结构框架下的机动信息估计

对于机动目标,在机动开始或结束时准确地改变滤波器结构是目标状态准确估计的前提。但由于无法准确得知目标的机动序列,通过设置机动探测器以准确探测机动的开始和结束。在目标机动初始阶段,虽然滤波器的估计协方差几乎保持不变,但其测量残差会增加,因此根据测量残差对机动的灵敏度,构造如下机动开始检测器:

(37)

(38)

若满足:

(39)

类似地,构造如下机动终止检测器：

(40)

(41)

与交互多模型算法相比,变结构滤波框架不需要同时运行多个滤波器,而是通过机动检测器判断机动的开始和结束,从而实现不同滤波器之间的切换,计算量较少,适用于本文中目标的受力场景。对于机动目标,滤波器在目标机动时切换为AUKF,可以对目标的位置、速度和机动加速度信息进行估计,在目标非机动时则采用UKF;对于非机动目标,则一直采用UKF进行状态更新,以避免AUKF降低跟踪精度。

3 跟踪滤波性能评估

基于低轨星网的多目标协同识别与跟踪是一个多传感器多目标问题,跟踪目标的卫星个数随时间变化,且由于多目标轨迹的不同,星网对每个目标的跟踪效果也会有差异。为评估星网对多目标跟踪识别性能,本文从对多目标的关联准确度以及对多目标的跟踪精度两个方面建立评价指标。

(42)

(43)

其中,N(k)表示对目标k的采样总个数。

由于本文研究的是星网对多目标的识别与跟踪问题,为了研究不同算法的性能对比,只考虑单个目标的跟踪精度过于片面,由此需要引入一个指标综合考虑对多个目标的估计结果。

为了评估多目标跟踪问题的性能,将最优子模式分配(optical sub-pattern assignment, OSPA)距离应用于星网对多目标状态估计的误差分析。OSPA距离可以理解为p阶逐对象式误差。这个误差由本地误差和势误差组成。定义多目标t时刻的状态估计值和真实值集合为

(44)

(45)

式中:Mt和Nt分别表示估计值集合和真实值集合,两个集合的势分别为mt和nt。对于任意正整数n∈N={1,2,…,n},Πn表示{1,2,…,n}排列的集合。OSPA距离定义为

(46)

(47)

式中:p为与阶数相关的参数,决定了OSPA距离对错误估值的灵敏度;d(c)(Mi,Nπ(i))表示两个向量之间的截断欧式距离:

(48)

式中:d(Mi,Nπ(i))表示欧式距离,即

(49)

其中,c表示截断参数。采用截断欧式距离是为了避免某个估计值发散或估计值与真实值不匹配而导致的评估指标失效。

(50)

式中:c决定了分配给本地误差和势误差的相对权重。

4 仿真分析

为了验证所提出的多目标数据关联与状态估计算法的有效性和适用性,本节进行了数值仿真。仿真时长和采样间隔分别设置为1 700 s和1 s,仿真开始时间设置为2020年11月25日04:00:00.00。考虑星基光学系统建立在构型如表1所示的Walker Delta型星座上;同时考虑如表2所示的多个目标。为了验证所提算法的有效性,分别在多目标机动和非机动场景下利用星网对多目标进行跟踪。

表1 星座构型

表2 多目标信息

4.1 非机动场景下仿真验证

目标相距越近,目标的识别难度越高。为了验证算法的有效性,设计目标1和目标3的运动轨迹相距很近,目标2和目标5的落点相近。在目标非机动的情况下,多目标的真实运动轨迹如图3所示。

图4为非机动场景下星网中可探测到目标的卫星个数。从图中可以看出,由于目标和卫星均处于运动状态,跟踪目标的卫星数量实时变化,若在星间接力的过程中无法准确识别目标,则无法实现目标的连续跟踪,或者导致滤波发散。图5和图6分别是采用本文算法得到的多目标位置和速度跟踪误差。从图中可知本文所提出的滤波器能够有效地利用星网实现多目标的识别跟踪,对目标速度的估计误差值大约500 s后就可以收敛到0.02 km/s以下,但是由于多传感器间接力跟踪的缘故,对位置的估计误差没有收敛到某一值附近,但是依然保持在10 km以下。

表3给出了非机动场景下星网对各个目标的MAA,从表中可以看出,对目标的MAA均在91%以上。但值得注意的是,分配精度会在某些时刻下降。这是因为在这些时刻,目标的实际位置非常相近,且由于跟踪的无源性,其在像平面的角轨迹更容易相互覆盖。虽然目标位置较近时对MAA有所影响,但是由于本文采用了卡方分布的原理,只采用较为可靠的量测值,在仅采用角轨迹的情况下依然能对多目标状态进行准确估计。

表3 非机动场景下各目标的MAA

4.2 机动场景下仿真验证

一旦目标进行机动,由于目标的非合作特性,因此无法提前获知目标的机动序列,这会导致动力学模型的不准确,进而导致对目标状态估计精度的降低。为此,本节测试了在目标机动场景下算法的性能。多目标的机动信息如表4所示。其中目标1、目标2、目标4为机动目标,机动开始/结束时间、机动幅度各不相同。值得注意的是由于这些目标的非合作特性,天基光学系统无法预先得知目标的机动信息。图7展示了机动场景下5个目标的真实运动轨迹。

表4 多目标初始状态和机动信息

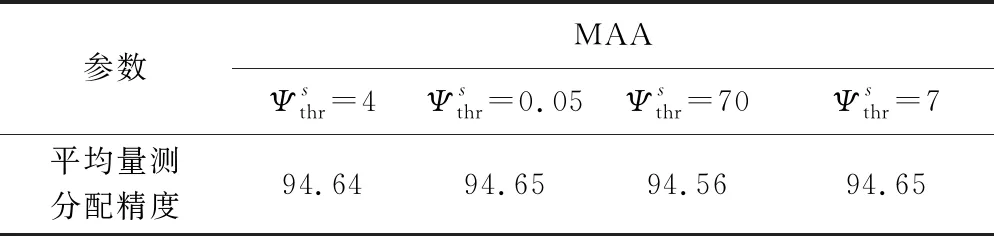
表5 机动场景下平均MAA

4.3 与其他算法的对比分析

利用低轨星网对多目标的识别跟踪分为数据关联阶段和多目标状态更新阶段,且这两个阶段是迭代进行,为了验证本文算法的有效性,本节采用不同的多目标状态更新算法。将以VSUKF与AEKF、UKF和AUKF为状态更新算法进行仿真对比,对比结果如图10和表6所示。从表6中可以看出,VSUKF的MAA最高,说明在目标机动情况,与本节提到的其他算法相比,采用VSUKF作状态更新滤波器的算法下可以对多目标进行更准确的数据关联。从图10可以看出,AEKF算法对位置和速度估计的OSPA距离明显大于VSUKF和AUKF算法,这说明UKF算法的线性化误差小于EKF算法,即UT变换比一阶泰勒展开能更好地对非线性系统进行近似。从图10(b)的结果可以看出,UKF算法在对目标速度估计方面比其他算法有更好的性能,而从图10 (a)对目标位置的结果可以看出UKF在初始阶段的OSPA距离相对较小,但在t=419 s时对目标位置估计的OSPA距离开始明显增大,而这恰好是机动开始的时刻。这表明UKF在无机动情况下性能良好,但在目标机动时对位置的估计误差显著增大。t在0～750 s时AUKF的位置估计和速度估计的OSPA距离与VSUKF相似,而t在750～1 000 s时VSUKF的性能优于AUKF。这是因为t在750～1 000 s时目标未发生机动,均方误差矩阵已经经过足够的时间收敛到一个稳定的值。因此,本文提出的VSUKF已经切换到标准UKF,使得VSUKF和UKF对速度估计的OSPA距离几乎相同,如图10(b)所示。由此说明本文采用的VSUKF算法在机动和非机动阶段都能得到满意的估计,且与AUKF相比,它的计算量更小。

表6 不同算法的MAA

从以上仿真对比中可以看出,当目标处于非机动阶段时,采用UKF算法的状态估计精度要明显高于AUKF算法;但是当目标处于机动状态,由于UKF算法没有考虑目标的机动特性,导致目标动力学模型不能准确反映实际情况,估计误差增大,而AUKF算法则实现了较高的估计精度。本文提出的变结构滤波框架综合考虑了估计精度和算法的计算量,通过机动检测器进行UKF和AUKF之间的切换,既减少了计算量,又提高了估计精度。在本文提出的算法中,多目标数据关联与目标状态更新过程是迭代进行,紧密相连的,所以在VSUKF算法进行状态更新基础上进行的数据关联结果也是较为准确的。

5 结 论

为了解决低轨星网对多目标的跟踪问题,本文提出了基于卡方分布的多目标数据关联算法和基于UKF滤波的多目标状态更新算法。根据多目标在量测平面的量测残差,基于卡方分布的假设,计算量测分配矩阵,在此基础上,通过变结构滤波框架和UKF滤波对多目标的位置、速度和加速度信息进行估计。仿真结果表明,该算法在目标机动和非机动情况下均有效,且在较低的计算量下能够达到与UKF和AUKF几乎相同的估计性能。