基于鲁棒EKF的MEMS-INS/GNSS/VO组合导航方法

李文华, 汪立新, 沈 强, 李 灿, 吴宗收

(火箭军工程大学导弹工程学院, 陕西 西安 710025)

0 引 言

随着导航技术的不断发展,各种导航手段和数据处理方法不断涌现,组合导航和信息融合技术的研究和发展方兴未艾。多源传感器信息融合系统相比于单一传感器系统具有更高精度和稳定性,尤其在各种复杂环境下仍可实现长时间高精度导航。传统惯导/卫导组合导航在各导航邻域已得到广泛的应用,但在卫星信号受干扰无法使用时难以保证导航精度,在复杂环境下稳定性较差。

微机械惯性导航系统(micro-electro-mechanical system, inertial navigation system, MEMS-INS)体积小、成本低,但精度较差;全球导航卫星系统(global navigation satellite system,GNSS)定位精度高,实时性好;视觉里程计(visual odometry, VO)自主性强,可以提供较高精度位置、姿态信息,近年来发展迅速。为此,构建基于MEMS的INS/GNSS/VO组合导航方法以提升导航系统在复杂环境下的可靠性和稳定性,且整个导航系统体积小、成本低、可适用性强。

目前,卡尔曼滤波(Kalman filter, KF)方法在组合导航中应用广泛,但是当建立模型不准确、外界扰动较大时,卡尔曼滤波算法容易发散,且标准KF仅适用于线性系统。针对非线性系统,最常用和有效的方法是扩展KF(extended KF, EKF),但EKF依然无法克服观测量受噪声干扰时对导航精度的影响,鲁棒性较差。

1964年,Huber结合两种范数提出了广义极大似然估计方法,即Huber方法,其鲁棒性优于基于范数的估计方法。针对系统存在异常观测值的问题,研究者们将Huber方法或对其改进后与KF结合起来进行组合导航,以提升导航系统的鲁棒性,但KF不适用于非线性系统,而组合导航系统往往是非线性的。文献[15-17]将Huber方法与非线性滤波方法结合起来进行组合导航,取得不错的效果。

针对以上问题,本文将Huber方法与EKF融合,提出一种基于鲁棒EKF的MEMS-INS/GNSS/VO组合导航方法,以有效提升系统在复杂环境下以及观测量受噪声干扰时的可靠性和鲁棒性。

1 组合导航滤波模型

本文构建的MEMS-INS/GNSS/VO组合导航系统以INS为主,当GNSS信号有效时,采用MEMS-INS/GNSS组合导航,当GNSS信号无效时,采用MEMS-INS/VO组合导航。

建立组合导航系统的线性滤波模型如下:

(1)

式中:为状态向量;为量测向量;-1为状态一步转移矩阵,可参考文献[4]进行设置;为量测矩阵;是均值为0方差阵为的系统噪声向量;是均值为0方差阵为的量测噪声向量。

选取15维状态向量如下:

(2)

当GNSS信号有效时,选取INS和GNSS的速度误差和位置误差作为组合导航系统的观测量:

(3)

对应量测噪声协方差阵由GNSS接收机速度量测噪声和位置量测噪声构成,对应的量测矩阵如下:

=[,,]

(4)

VO可以提供较为精确的姿态和位置信息,但VO提供的是以第一帧图像为参考坐标系的世界坐标系下的结果,需转换到地理导航坐标系(系)下。当GNSS信号无效时,选取INS和VO的姿态误差和位置误差作为组合导航系统的观测量:

(5)

对应量测噪声协方差阵由VO速度量测噪声和位置量测噪声构成,对应的量测矩阵如下:

(6)

(7)

2 基于Huber的鲁棒EKF

在工程实践中遇到的导航系统往往是非线性的,即系统方程和量测方程均是非线性的。EKF可解决系统方程和量测方程均为非线性时的估计。EKF是对原系统和量测先进行泰勒级数展开,略去高阶项后近似为线性系统,再应用第一节所建模型作线性Kalman滤波估计。

假设系统非线性模型如下:

(8)

则EKF方程如下:

(9)

基于KF或EKF的导航系统在复杂环境下易受到干扰,异常观测值会严重影响导航精度,鲁棒性较差。而Huber滤波方法通过重新构造量测噪声协方差阵可以有效降低异常观测值对系统的影响,提升系统的鲁棒性。

Huber代价函数结合了和范数的特性,是Huber所提出的M估计中最常用的代价函数,其表达式如下:

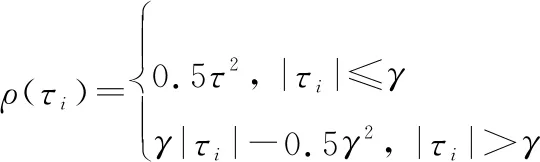
(10)

Huber权值函数表达式如下:

(11)

式中:()由()求导所得,即()=′()。

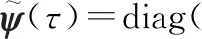
(12)

利用式(12)对量测噪声协方差矩阵进行修正,得到修正后的量测噪声协方差阵如下:

(13)

用式(13)替代式(9)中的量测噪声协方差阵,即为基于Huber的鲁棒EKF算法(robust extended Kalman filter based on huber method, HREKF)。HREKF本质上是对量测噪声协方差阵进行重加权,对不同大小的观测残差构造不同的权重,进而重构量测噪声协方差阵,以克服异常观测值对导航精度的影响,达到提升系统鲁棒性的目的。HREKF的详细步骤如下:

由式(12)构造权值矩阵,并根据式(13)计算修正后的量测噪声协方差阵;

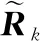
3 试验与分析

为验证所提方法可靠性和鲁棒性,采用仿真试验和KITTI数据集中一段行车轨迹进行分析。

3.1 仿真试验

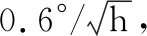
设计一个持续1 300 s的运动轨迹,如图1所示,包含加减速、直线、转弯、爬坡、下坡等机动动作。

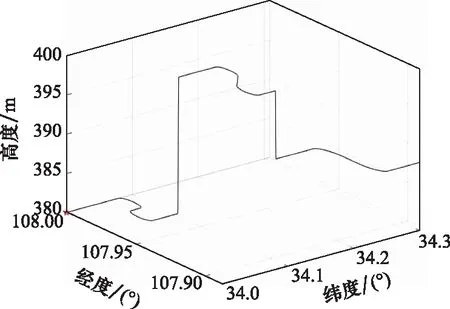
图1 运动轨迹

为验证所提方法在传感器有效性改变情况下的可靠性以及存在异常观测值情况下的鲁棒性,设置大角度的初始姿态误差为[1°,1°,5°];设置GNSS信号在630～650 s、700～720 s期间不可用;在400～500 s、800～900 s期间加入混合高斯噪声:

=(1-)+

(14)

式中:为污染分布的比值;为污染高斯噪声的概率分布;为GNSS输出信息的概率分布;为干扰分布。

在1 100～1 200 s期间异常,即将量测噪声的幅值调大4倍;并采用Sage-Husa量测噪声自适应KF (adaptive KF, AKF)、EKF和所提HREKF算法的滤波结果进行对比分析。

式(14)所示的分布被称为污染高斯分布,当干扰分布为具有较大标准偏差的高斯分布时,污染高斯分布也被称为混合高斯分布。本文中设置干扰分布的标准差为GNSS信号的20倍,污染分布的比值为01。

基于3种滤波方法的MEMS-INS/GNSS/VO组合导航系统仿真结果如图2～图4所示。由图2～图4可以看出,在整个时间段内3种滤波方法都能保持较高精度,且当GNSS信号在630～650 s、700～720 s期间不可用时,VO的引入仍可约束惯导的累积误差,输出较高精度的导航结果。其中,水平位置误差在15 m以内,水平速度误差在1.5 m/s以内,水平姿态误差在130′以内,验证了INS/GNSS/VO组合导航系统的可靠性。

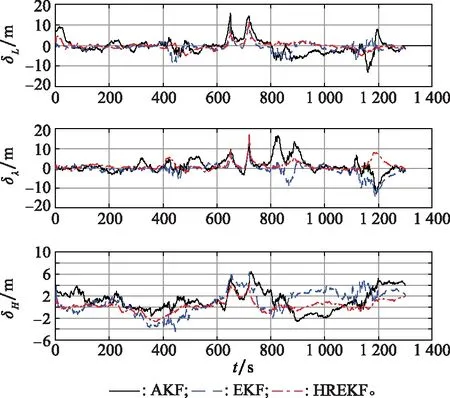
图2 仿真实验位置误差

图3 仿真实验速度误差

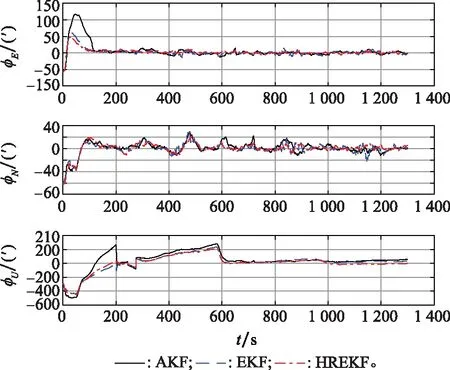
图4 仿真实验姿态误差

对比图2～图4中3种滤波方法误差结果,可以看出,HREKF算法融合结果的精度都高于AKF和EKF,且当存在大角度的初始姿态误差时,HREKF的滤波结果相较于AKF和EKF可以更快更准确的收敛,说明HREKF算法能够较好地处理非线性系统。当GNSS输出信号受到污染以及在4倍初始误差情形下,AKF和EKF滤波效果变差,对导航精度影响较大,但HREKF通过重构量测噪声协方差阵,降低了误差的发散程度,仍能输出较高精度结果,表明了所提HREKF算法有较强的鲁棒性。

为定量分析不同滤波方法、不同情形对导航系统精度的影响,分别计算了在全时段(0～1 300 s)、混合高斯噪声(800～900 s)和4倍初始误差(1 100～1 200 s)下3种滤波方法各导航参数结果的均方根误差(root mean square error, RMSE),如表1所示。

表1 仿真实验各参数RMSE

从表1中可以看出,HREKF各导航参数的RMSE在全时段都优于AKF和EKF,尤其在混合高斯噪声和4倍初始误差情形下,HREKF的导航精度明显优于AKF和EKF,进一步表明了基于HREKF的MEMS-INS/GNSS/VO组合导航方法的可靠性和鲁棒性。

3.2 KITTI数据集验证

为验证本文所提组合导航方法在实际工程应用中的可靠性和有效性,采用KITTI数据集对其进行验证。KITTI数据集是目前国际上最大的自动驾驶场景评测数据集,该数据集提供多种传感器数据,其中包含基于MEMS的OXTS RT 3003惯性导航系统,2个灰度相机,2个彩色相机。

实验中采用KITTI数据集中的两段行车轨迹(“2011_09_26_drive_0036”和“2011_09_30_drive_0033”)对所提方法进行验证。原始IMU数据为100 Hz,矫正后灰度图像为10 Hz。采用ORB SLAM2框架对图像处理后的结果作为VO输出。陀螺漂移为36°/h,加速度计零偏为1 mg。以数据集中卫星信号提供的经纬度信息和水平速度信息作为参考基准。

KITTI数据集中2011_09_26_drive_0036序列卫星信号轨迹如图5所示,为验证本文方法性能,假设卫星信号在20～30 s、50～60 s期间无效;2011_09_30_drive_0033序列的卫星信号轨迹如图6所示,假设卫星信号在50～60 s、125～145 s期间无效;并采用Sage-Husa量测噪声AKF,EKF和HREKF算法的滤波结果进行对比分析。

图5 drive_0036运动轨迹

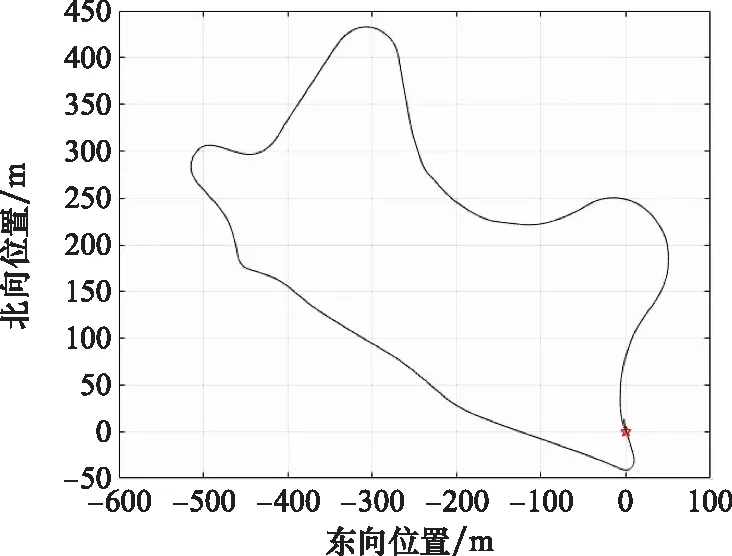
图6 drive_0033运动轨迹

对两个序列采用3种滤波方法进行组合导航的水平位置和速度误差结果如图7～图10所示。从图中可以看出,当卫星信号失效时,VO的加入仍可约束惯导的累积误差,输出较高精度的导航结果,在卫星信号失效20 s的情形下,水平定位误差保持在12.5 m以内。

图7 drive_0036水平位置误差

图8 drive_0036水平速度误差

图9 drive_0033水平位置误差

图10 drive_0033水平速度误差

为定量分析不同滤波方法在实际场景下的导航精度,计算了2011_09_30_drive_0033序列的水平位置和速度RMSE,如表2所示。从表2中可以看出,HREKF的水平位置和速度RMSE结果均优于AKF和EKF,而EKF将量测噪声协方差阵设置为固定值,其导航精度有时会低于AKF,但HREKF通过修正量测噪声协方差阵,可以输出较高精度导航结果,验证了基于HREKF的INS/GNSS/VO组合导航方法拥有较高的可靠性和鲁棒性。

表2 drive_0033中各参数RMSE

4 结 论

本文研究了基于鲁棒EKF的INS/GNSS/VO组合导航方法,将EKF算法与Huber方法结合,并在传统卫星/惯导组合导航方式基础上加入了VO。仿真和KITTI数据集实验结果表明,组合导航系统在GNSS信号失效时仍能输出较高精度的导航结果,且HREKF滤波结果相较于AKF和EKF拥有更高的精度和鲁棒性,验证了提出组合导航方法的可靠性和鲁棒性,非常适用于成本低、体积小的工程应用背景。