PMSM比例谐振自抗扰电流谐波抑制方法

方 淳,陈 哲,窦满峰

(1.航空工业第一飞机设计研究院，西安710089；2.西北工业大学，西安710129)

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因控制精度高转矩脉动小而广泛应用于航空机电系统驱动与伺服机构中。在燃油泵、液冷泵和风机类负载场景应用中，PMSM无位置传感器控制技术代替旋转变压器，降低了电机本体体积重量，对应解码电路的取消也提升了驱动器与不同系统PMSM的通用适配性，使机电系统的保障性与维护性得到提升。

永磁同步电机转子位置估计依赖静止参考系下的电压和电流信号的质量。其中电压是指令电压，理想情况下谐波含量较小，而电流是实际采样的电流，在机载燃油、液冷系统驱动用PMSM在零下50℃起动时，由于液体介质低温下粘滞性增加，导致典型泵类负载特性曲线出现非线性负载扰动，在电机端产生大量电流噪声与高次谐波。在dq轴坐标系下，上述谐波表现为6k次谐波分量，这其中6次谐波的幅值最高，影响程度最大[1]。谐波电流使PMSM三相电流发生畸变，难以从估计反电动势中准确地估算转子位置和速度[2-7]，造成电机无位置传感器控制性能下降，影响航空机电系统低温环境适应性。

抑制电流谐波对提高PMSM无位置控制性能尤为重要。从控制角度而言，电流谐波抑制需要针对系统内外扰动所造成的稳态误差进行补偿。文献[3]采用多个旋转坐标系下的PI控制器，通过实时提取谐波电流并注入谐波电压从而消除电机电流中的谐波，然而该算法实现复杂。文献[4]提出一种基于比例谐振的电流规划控制方法，该方法根据规划电流轨迹的傅里叶展开，采用基于比例谐振的电流环分别实现对电流基波和主要高次谐波的控制。文献[5]采用比例谐振控制器(PR)来抑制电压电流谐波。文献[6]提出一种基于PR和自抗扰控制器(ARDC)简单 串联的结构，降低了并网电流中的谐波含量。

本文为抑制电流谐波的影响，提升永磁同步电机转子位置估计的精度，提出一种基于PR-ADRC的电流环控制策略，在扩展状态观测器(Extended State Observer，ESO)的前馈通道中融入比例谐振控制器，抑制6次电流谐波。本文给出了ESO和QPLL正交锁相环(Quadrature Phase Locked Loop，QPLL)对转子位置速度的估计原理，分析传递函数并给出了PR-ADRC电流环的参数选取和稳定性证明，并通过实验验证了6次谐波电流抑制后的反电动势和转速估算精度改善效果。

1 转子位置速度估计

1.1 电机数学模型

在旋转参考系下dq轴电流控制中采用PR-ADRC取代传统的PI控制器。电机dq轴电流动态方程可以描述为

(1)

转子位置、速度估算方法依赖于静止参考系中的电流电压矢量[7]。忽略电机的非对称性以及饱和效应、涡流损耗等情况，PMSM在静止参考系下电压动态方程可表示为

(2)

式中,p是微分算子，uαβ=[uαuβ]T表示定子电压矢量，同样静止参考系上的电流动态方程可表示为

(3)

其中，iαβ=[iαiβ]T表示定子电流矢量，eαβ=[eαeβ]T为反电动势矢量，可表示为

eαβ=ωeψf[-sinθecosθe]T

(4)

式中,ωe和θe分别表示转子角速度和位置。

1.2 ESO估算反电动势设计

根据上述电机模型，考虑稳定性条件[8]，构建ESO估算反电动势方案如图1所示。

图1 自适应ESO对反电动势的估算流程图

图中,iαβ和uαβ是系统输入，eαβ是系统的未知扰动，系统输入和集中扰动可表示为

(5)

建立对应ESO方程：

(6)

其中,Z1=[Z1αZ1β]T和Z2=[Z2αZ2β]T分别表示估计的定子电流和估计的集中扰动，β1β2为观测器增益，估计误差为ε1=[ε1αε1β]T。

当ESO稳定时，定子电流的估计值和集中扰动将收敛至真实值。因此反电动势的估计值可表示为

(7)

1.3 正交锁相环(QPLL)设计

本文采用反电动势标幺化的QPLL从估算反电动势中提取转子速度和位置信息。QPLL结构如图2所示。反电动势的幅值在不同的工作速度下发生变化，通过标幺化QPLL依然可以提供较好的位置和速度估计效果。QPLL闭环传递函数为

(8)

图2 QPLL估算转子位置速度流程图

2 电流谐波抑制策略

2.1 PR-ADRC电流环设计

为抑制电流谐波，改善系统动态响应和参数摄动。本文采用基于PR控制器的ADRC的设计方法。以q轴电流环为例，PR-ADRC结构如图3所示。

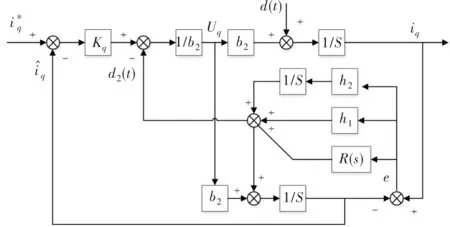
图3 基于PR控制器的PR-ADRC结构框图

与PI控制器相比，PR-ADRC的优势为加入了谐振控制器R(s)。本文采用准谐振控制器实现对一定频率带宽的抑制，同时可根据实际情况并联多个谐振控制器，对已标定的不同频率谐波进行抑制。其传递函数为

(9)

式中,Kr为谐振控制器的增益；ωc为谐振控制器的带宽；ω1为谐振频率。根据前文分析，在ADRC的ESO中添加6次谐波的谐振控制器，削弱6次谐波电流，改善转子位置估计精度。

ADRC数学表达：

(10)

前馈通道h1和R(s)构成一个PR控制器，且：

(11)

通过上述两步改进，最终系统的扰动传递函数Gf2(s)可表示为

(12)

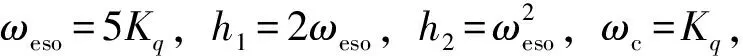
2.2 PR-ADRC电流环控制稳定性分析

系统的零极点分布如图4所示。随着Kq的增加，所有的极点都远离虚轴，并且所以极点都在s平面的左半部分，这证明了系统是稳定的。

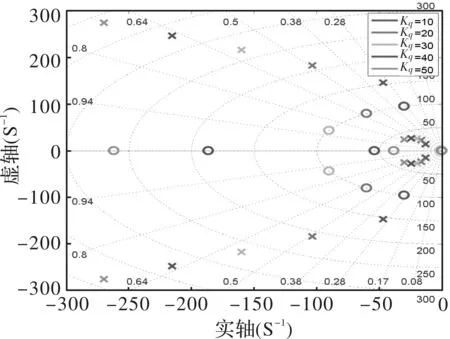
图4 不同Kq值下的系统零极点图

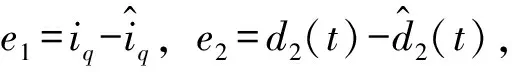
(13)

系统状态矩阵为Hurwitz矩阵，因此系统是渐近稳定的。

本文设计的永磁同步电机控制无位置传感器控制方案的整体框架如图5所示。其中图2、图3分别对应ESO和QPLL的设计方案。电流环基于PR-ADRC改进控制，速度环基于常规PI控制。

图5 基于PR-ADRC的电机控制整体框架

3 实验验证

3.1 实验平台及实验条件介绍

在Higale半物理仿真平台上用某型燃油泵驱动用永磁同步电机对所提方法进行实验验证。实验平台如图6所示。

图6 实验平台

被控电机参数如表1所示。

表1 200 W永磁同步电机参数

实验中，PWM开关频率为8 kHz，给定负载转矩为0.5 Nm，给定转速为750 r/min，对应基波频率为50 Hz。为了保证实验对比的公正性，实验中速度环均采用带宽为60 rad/s的PI控制器，且电流环控制器带宽设置均为400 rad/s，而PR-ADRC控制器的参数设置如下：Kq=400rad/s，ωeso=2000 rad/s，Kr=2000，ω1=150 rad/s。

3.2 负载电流FFT分析对比

为了验证改进后电流环降低三相电流谐波的效果，图7和图8分别给出了在死区时间为2 μs，转速为750 r/min，负载转矩为0.5 Nm下基于传统PI控制器和基于PR-ADRC控制器的FFT分析结果图。

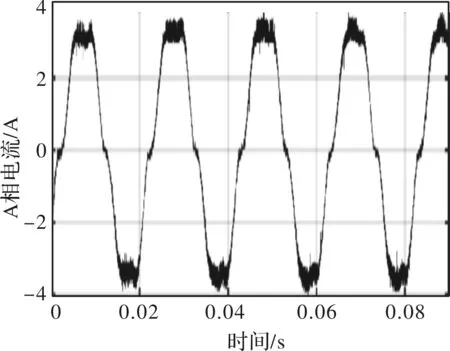
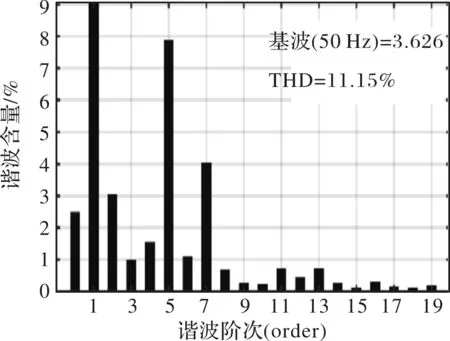
图7 基于PI控制器的FFT分析

图8 基于PR-ADRC控制器的FFT分析

图7基于常规PI控制器方法结果中，A相电流中含有明显的5次和7次谐波，总谐波失真THD为11.15%。图8基于电流环PR-ADRC控制结果显示， A相电流中的5次和7次谐波电流下降超过50%，其总谐波失真THD下降为6.15%。后者对于谐波电流抑制效果明显。

3.3 反电动势及位置速度估计对比

进一步验证改进后电流环的反电动势和位置速度估计效果，图9和图10分别给出了在转速为750 r/min，负载转矩为0.5 Nm下，稳态时基于传统PI控制器和基于PR-ADRC控制器的反电动势和位置速度估计的实验结果。

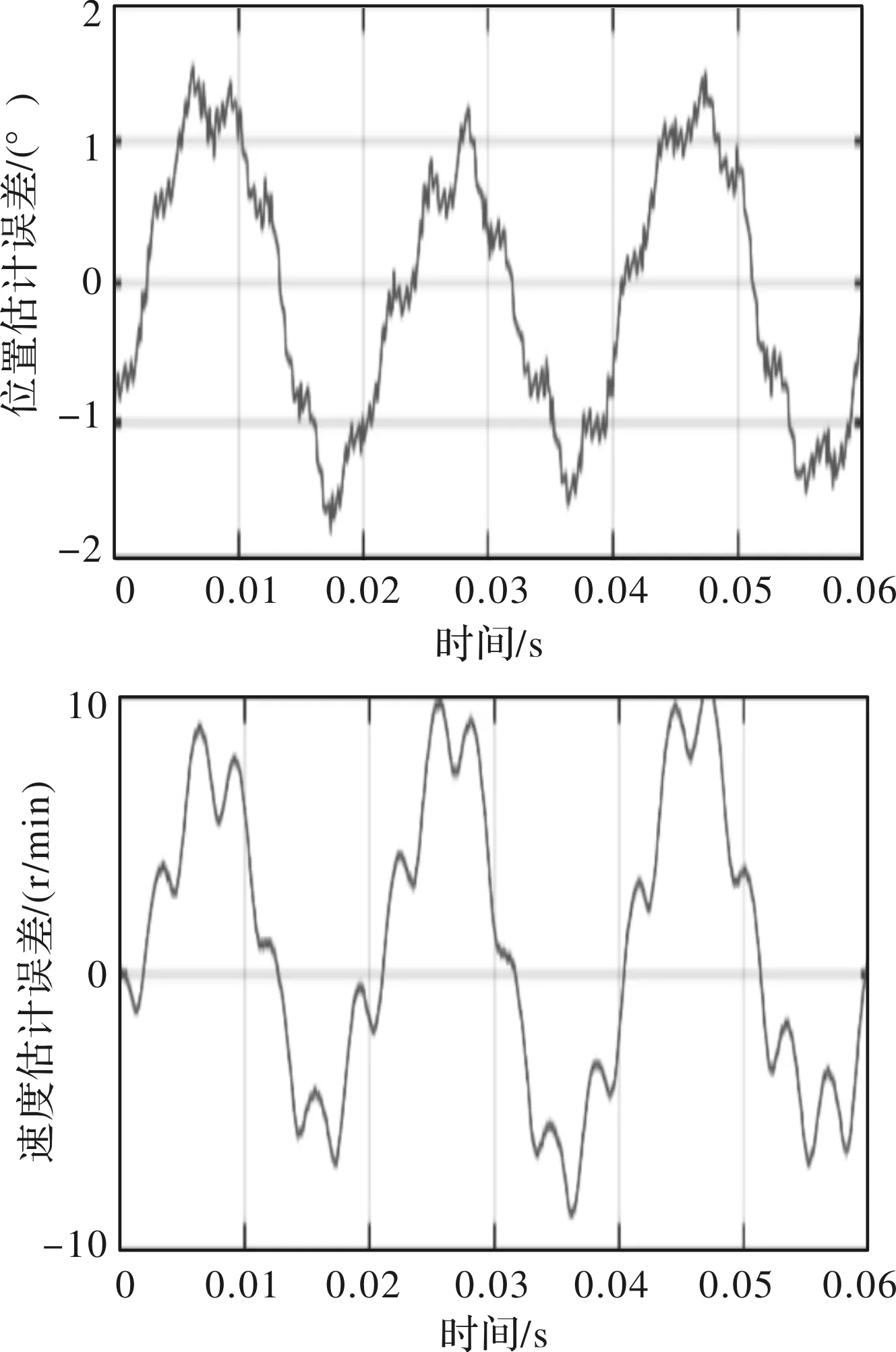
图9 基于PI控制器的电动势和位置速度估计结果

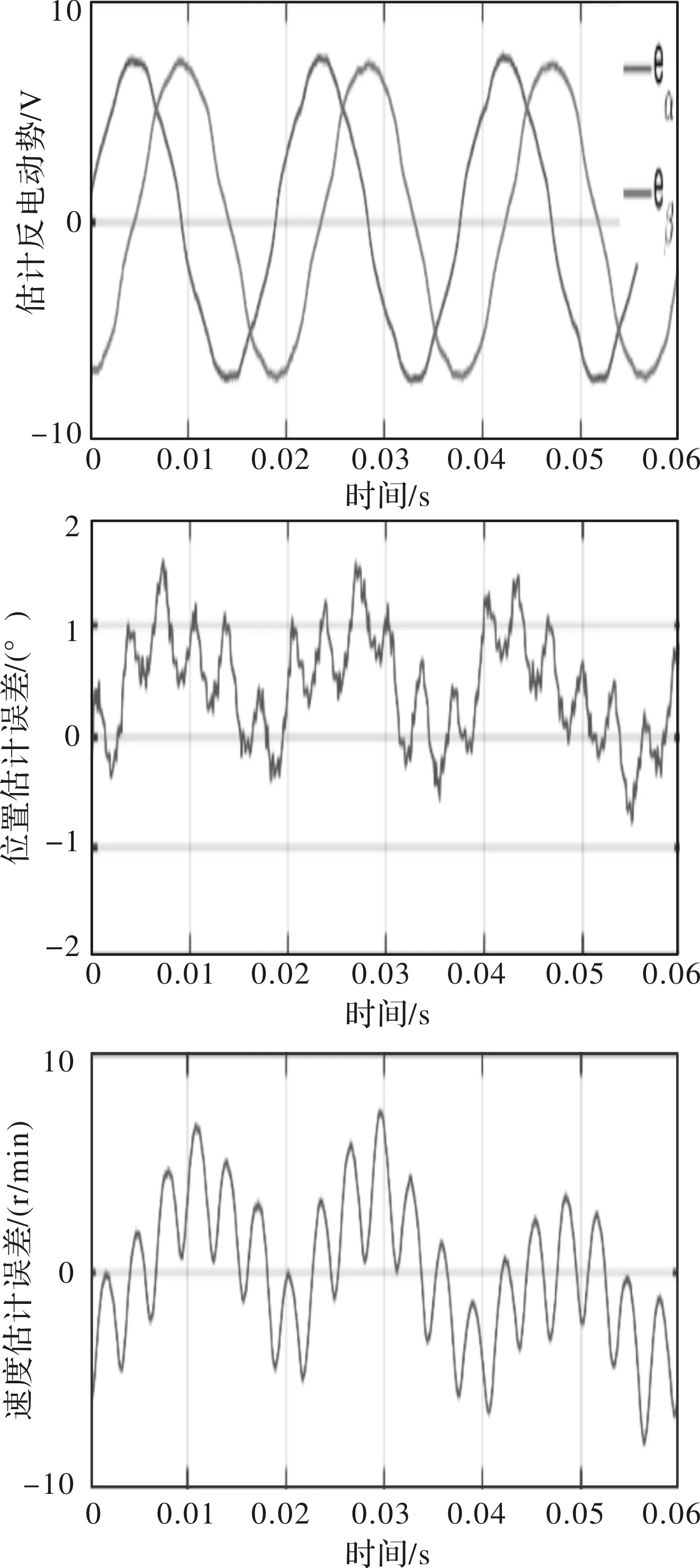
图10 基于PR-ADRC控制器的电动势和位置速度估计结果

常规PI电流环控制方法的转子位置和速度估计误差分别为(-1.7°，+1.5°)和±10 r/min；PR-ADRC电流环控制方法的转子位置和速度估计误差分别为(-0.7°，+1.5°)和±7 r/min，PR-ADRC电流环控制方法的误差更小。实验结果证明，采用基于PR-ADRC方法的电流环控制器在对电机进行无位置控制时，具有更好的转子位置和速度估计效果。

4 结 论

本文针对航空燃油、液冷泵类系统低温液体粘滞导致永磁同步电机无位置传感器控制精度下降的问题，在dq轴旋转坐标系以及αβ轴静止坐标系下对永磁同步电机进行了建模分析。设计了扩展状态观测器结合正交锁相环技术的无位置传感器控制方法，并分析了电流谐波产生的原因。为加强对谐波电流的抑制效果，提升低温环境泵负载的无位置控制精度，本文提出了一种基于比例谐振与自抗扰控制的PR-ADRC电流环控制策略。实验证明采用基于PR-ADRC方法的电流环控制器对谐波电流抑制效果明显，在对低温环境的泵驱动电机进行无位置闭环控制时，可具有更好的环境适应性。