带多个信道的布尔控制网络可观测性

沈宇桐，徐 勇

(河北工业大学理学院，天津 300401)

0 引言

1969年，美国学者Kauffman提出一种用于刻画细胞与基因调控网络的模型—布尔网络(Boolean Networks，BNs)[1]。在该模型中，每个基因被抽象为一个网络节点，其状态表达可量化为0(不活跃)或1(活跃)，每个基因在t+1时刻的状态根据t时刻与其相邻基因的逻辑关系进行更新，因此在对所有基因的初始状态进行赋值后，相应的基因动态行为就能被确定。实际上BNs作为一种物理网络模型，可用一个网络图进行描述，图1为3个节点的BNs结构图。与其他网络相比，BNs结构简单，是最基础的2值逻辑动态系统，具有不动点、极限环等重要的拓扑结构，因此它的大部分结果可以推广到多值逻辑网络、混合值逻辑网络等网络系统。BNs在物理系统、生化系统及系统科学等实际系统中有着广泛的应用。例如：Albert等人[2]通过计算BNs的周期得到大型交互系统的一般路线图；Heidel等人[3]将确定BNs循环结构的方法应用到生化系统，验证了生化信号传导网络的结构可能存在混乱的猜想；Kauffman等人[4]利用随机布尔网络的稳定性证明了细胞的活态随着进化而变得更加稳定。

图1 布尔网络 Fig.1 Boolean networks

为了进一步研究BNs，将带有外部输入的BNs描述为布尔控制网络(Boolean Control Networks，BCNs)[5]。由于遗传网络具有逻辑性，且早期缺乏处理逻辑动态系统的适当工具，学者们对BCNs的研究成果有限。最近，程代展教授[6]提出一种新型代数工具——矩阵的半张量积(Semi-Tensor Product of Matrices，STP)。应用STP理论将布尔系统表示为离散的线性系统，解决了BNs中许多具有挑战性的问题，如稳定性与镇定性[7-8]、能控性与可观测性[9-10]、同步性[11-12]、最优控制与干扰解耦[13-14]及BNs的输出追踪与重构问题[15-17]。应用STP理论对BCNs相关问题进行研究已经成为一个热点课题。

在许多情况下，控制系统需要从输出数据中获取输入信息，因此分析系统的可观测性尤为重要。近年来，BNs可观测性的研究不仅为复杂系统的建模提供了新观点，也提供了一种利用外部输入操纵生物系统的方法。目前对BCNs可观测性的研究也越来越深入，文献[18]研究了布尔多层控制网络的可观测性并验证特殊层中每个节点的可观测条件；基于文献[18]，文献[19]进一步研究概率布尔多层网络的可观测性条件，并将其结果应用于癌细胞网络的监测；文献[20]提出利用布尔网络可达性验证系统可观测的方法；文献[21]进一步将布尔控制网络的可观性问题转化为集可控性问题，得到系统可观测性与重构性的相应结论。

可观测性在网络安全领域更是发挥着重要作用，被用来研究网络攻击和检测问题[22-25]。网络攻击作为外界的未知输入会对系统产生影响，为了更好检测系统的抗攻击能力，系统开发者需要观测未知输入存在时系统的状态[26]。近年来,学者们研究的多为输出从单个信道接收系统状态数据的BNs，文献[27]受文献[28]的启发，提出了依一定概率将状态数据运输到某个可被观测的输出信道的网络。

本文在文献[27]的基础上进行推广，首次提出带多个信道的BCNs模型，并给出模型可观测的条件与反馈控制器的设计算法。从网络安全角度，在攻击者决定攻击某个信道时，输入状态可能已从其他信道完成传输，使得攻击无效，大幅度提高了网络安全级别。

1 预备知识

本节介绍STP理论的相关符号、重要定义及引理。

定义2[6]给定A∈Mp×m，B∈Mq×m，矩阵A与B的Khatri-Rao积记作A*B，定义

A*B=[Col1(A)⊗Col1(B),…,Colr(A)⊗Colr(B)]∈Mpq×m

引理1[6]设f(x1,x2,…,xn)为一个逻辑函数，在向量形式下f:Dn→D存在唯一的逻辑矩阵Mf∈L2×2n，称为f的结构矩阵，使得

2 主要内容

2.1 带多个信道的布尔控制网络的代数表示

考虑BCNs：

(1)

xi(t+1)=Miu(t)x(t),i=1,2,…,n

(2)

对式(2)作Khatri-Rao积，得

x(t+1)=Lu(t)x(t)

(3)

其中，L=M1*M2*…*Mn,L∈L2n×2m+n。

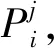
yi(t)=gi(x1(t),x2(t),…,xn(t)),i=1,2,…,p

系统式(1)的网络结构如图2所示，令E为所有可能输出的模态标识矩阵

图2 带多个信道的布尔控制网络Fig.2 Boolean control networks with multiple channels

对上式作Khatri-Rao积，

y(t)=Hix(t)

BCNs依一定概率在多个信道上进行选择性输出，采取期望表示

[y(t)]=H[x(t)]

(4)

2.2 带多个信道的布尔控制网络的可观测性

(5)

则带多个信道的BCNs式(3)和(4)是可观测的。

根据文献[27]中BNs的可观测性，本文给出带多个信道的BCNs可观测性定义，且与文献[18]中BCNs可观测性的定义不同。

基于带多个信道的BCNs式(3)和(4)的代数表示与可观测性定义3，给出该模型可观测的充要条件。

Colα(ϑs0)≠Colβ(ϑs0),α≠β

其中

⋮

[y(s0)]=HL(I2m⊗L(I2m⊗L(…(I2m⊗L(I2m⊗L)…)))))u(s0-1)u(s0-2)…u(0)x(0)

即

(6)

因为系统式(3)和(4)是可观测的，由定义3可知，线性方程式(6)关于未知向量x(0)的解是一一对应的，因此可得到Colα(ϑs0)≠Colβ(ϑs0),α≠β。

(7)

由式(7)可得

(8)

若式(8)不成立，即存在有限时间s′0∈{1,2,…,s0}，使得则在有限时间s′0下，存在α0≠β0，使得ϑϑ因此线性方程式(6)关于未知向量x(0)的解不是一一对应的，矛盾。

证明成立。

2.3 基于状态反馈控制的可观测性研究

考虑状态反馈控制

(9)

u(t)=Kx(t)

(10)

其中，K=K1*K2*…*Kn,K∈L2m×2n。

根据自由控制序列下系统式(3)和(4)的可观测性条件，结合文献[6]中的降阶矩阵Φn，即对于任意x∈Δ2n有x2=Φnx，给出系统式(3)和(4)在状态反馈控制下可观测的判定定理。

Colα(θs0)≠Colβ(θs0),α≠β

其中

证明：根据式(3)和(4)和式(10)，可得

⋮

[y(s0)]=Hx(s0)=Hx(0)

即

(11)

由定义3和式(11)可知：在状态反馈控制式(10)下，系统初始状态可以由输出序列唯一确定，类似于定理1的证明，线性方程式(11)有唯一的解当且仅当矩阵θs0的每一列均不相等，即对于给定的状态反馈控制式(10)，初始状态x(0)可由输出唯一确定，即

证明成立。

结合文献[27]中的定义3，本文给出带多个信道的BCNs式(3)和式(4)的输入状态x(0)由输出序列{y(0),y(1),…,y(s0)}可观测时，状态反馈控制的结构矩阵K的一种计算方法。

算法1

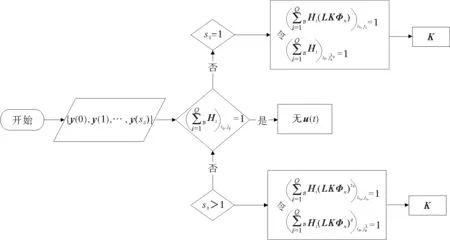
图3 算法1的流程图Fig.3 Flowchart of Algorithm 1

且满足

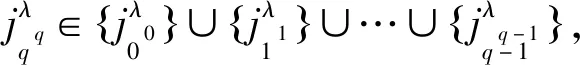
该算法的计算复杂度较高，仅适用于设计较小s0下状态反馈控制的结构矩阵K。

3 算例分析

给出以下两个例子验证本文结果的有效性。

例1考虑式(12)BCNs

(12)

输出网络为

(13)

假设y1(t)有2个信道，y2(t)有3个信道，即

(14)

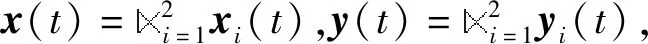
x(t+1)=Lu(t)x(t)

(15)

[y(t)]=H[x(t)]

(16)

采取状态反馈控制

(17)

将式(10)代入式(15)得x(t+1)=LKΦnx(t)，其中K=δ4[3,2,2,2]，Φn=δ16[1,6,11,16]。经计算：

例2考虑如式(18)的BCNs

(18)

输出网络为

(19)

假设y1(t)有2个信道，y2(t)有3个信道，即

(20)

经计算：H1=δ4[2,2,2,3]，H2=δ4[2,2,1,3]，H3=δ4[2,1,2,3]，H4=δ4[2,4,4,3]，H5=δ4[2,4,3,3]，H6=δ4[2,3,4,3]，L=δ4[4,2,3,3,3,1,4,4,4,2,3,3,1,3,2,2]。

应用算法1，构造状态反馈控制的结构矩阵K,使系统式(18)和式(19)的初始状态x(0)由输出序列{y(0),y(1)}可观测。

步骤1：当s0=0时，经计算

4 结论

本文提出带多个信道的BCNs模型，主要研究经多个信道选择性输出后，BCNs的可观测性问题。基于矩阵的半张量积理论，给出带多个信道的BCNs的代数表达，借助于该代数表示及可观测性定义，得到自由控制序列与状态反馈控制下，BCNs可观测的充分必要条件。最后，给出一种算法构造反馈控制矩阵，使得带多个信道的BCNs是可观测的。