一种基于校验矩阵的非系统卷积码识别方法

眭惠巧,赵一菲,李亮辉,温子欣

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北工业大学 人工智能与数据科学学院，天津 300401；3.天津理工大学 集成电路科学与工程学院，天津 300000)

0 引言

数字无线通信中，通信信号在通信信道传输过程中会受到各种加性噪声、信道衰落、码间串扰等影响而造成通信可靠性降低。为克服通信信道环境引起的通信质量下降，数字通信系统发送端通常采用信道编码技术增强发送信号在信道传输时抵御外界干扰的能力，在通信接收端采用相应的解码技术检测或纠正错码，从而提高通信可靠性[1-2]。

合作通信条件下，收发双方根据通信链路设计时选定的编码方式和参数进行编码和译码。通信侦察和非协作通信中，接收方对通信发送端采用的信道编码方式完全未知，为侦听敌方通信信号中传输的信息，需先对通信发送端采用的信道编码方式进行识别[3]。

信道编码根据监督元与信息组的关系，分为分组码和卷积码两大类，其中卷积码由于充分利用了各码组之间的相关性具有良好的性能应用，且码长和信息位较小，因此在码率和设备复杂性相同的条件下，卷积码的性能均优于分组码，应用越来越广泛，尤其非系统卷积码在现代卫星通信中具有重要地位，对非系统卷积码识别具有重要意义。

实际工程应用中，数字通信系统设计通常结合使用帧同步、信道编码、伪随机扰乱、交织编码、CRC校验等多项技术来实现接收方和发送方的同步以及提高系统传输性能[4]。因此，工程应用中对包括卷积码在内的信道编码识别通常结合帧同步、帧长、协议等分析结果，通过试解码和CRC校验来判定，且对有限集合进行试解码需要大量数据，存在运算量大、效率低等问题。基于理论分析识别方法主要有欧几里德算法[5-6]、Walsh-Hadamard分析法[7]、高斯消元法[8]等，这些方法仅适用于(n,1,m)卷积码，且运算量大，工程实用性不高。

本文给出了一种基于校验矩阵的识别方法，对有限集合内非系统卷积码进行校验识别，适用于(n,k,m)编码，运算量小，便于工程实现。

1 卷积码的矩阵

卷积码构造简单，性能优越，但其数学理论不如循环码完整严密。卷积码的编码器可以看作一个由k0个输入端和n0个输出端组成的时序网络，卷积码编码器某时刻的输出不仅与该时刻输入编码器的信息组有关，而且与以前若干时刻输入编码器的m组信息有关，通常以编码约束度m表示相互约束的子码个数。卷积码一般用(n0，k0，m)表示。n0为子码长度，k0为对应一个子码输入的信息码个数。如果在n0位长的子码中，前k0位是原输入的信息码，则称该卷积码为系统码，否则称为非系统码[9]。

卷积码的描述方式有矩阵描述法、多项式描述法和树图描述法，其中矩阵描述法更适合于理论的分析。一个卷积码可以完全由监督矩阵H∞或生成矩阵G∞所确定，(n0，k0，m)卷积码的生成矩阵和监督矩阵的一般形式为：

并且二者存在下列关系：

式中，G∞和H∞分别由它们的第一行和第一列决定，记为g∞和h∞，称为基本生成矩阵和基本校验矩阵。

基本生成矩阵和基本校验矩阵也可以用多项式表示：

g(D)=g0+g1D+…+gmDm，

h(D)=h0+h1D+…+hmDm。

在g∞中g0g1…gm为k0×n0阶非零矩阵，其余元素均为0矩阵，而在h∞中h0h1…hm则为(n0-k0)×n0阶非零矩阵，其余元素均为0矩阵。矩阵gi和hii∈[0,1,…,m]的每个元素取值为1或0。

由于一个卷积码的h∞矩阵一旦确定，码的监督矩阵H∞和生成矩阵G∞也就完全确定了，因此h∞是决定码的很重要的矩阵。

从上述分析可以看出一个卷积码由参数n0、k0、m和一个长度为(n0-k0)×n0×(m+1)的非零向量h∞决定，向量的每个元素取值为1或0。

2 非系统卷积码的识别

2.1 非系统卷积码识别原理

假设一个卷积码编码器的输入序列d∞和输出序列C∞可以分别表示为：

d∞=(d0,d1,d2,…)，

C∞=(C0,C1,C2,…)，

二者都是半无限序列并且存在下列关系：

C∞=d∞G∞。

因为非系统卷积码的生成矩阵和校验矩阵也存在下列关系：

因此容易得到：

H∞由h∞决定，并且h∞中仅有m+1个非零矩阵h0h1…hm，因此有：

其中，i∈[-∞,+∞]为整数。

假设编码后的序列C∞经过信道传输后在接收端接收到的未进行解码的序列为：

其中，Ci和ri均为1×n0阶矩阵。

当信号在传输中未引入错误码时，有C∞=r∞，因此有下列关系成立：

利用该关系可以进行卷积码的盲识别，乘积为0认为校验通过，否则为不通过。实际中可取一定量数据进行计算，设定校验通过率门限，依据大量数据校验结果与门限的比较确定接收码序列是否采用该非系统卷积编码以及采用卷积码的参数n0、k0、m。

2.2 非系统卷积码识别的实现

上节介绍了对非系统卷积码校验识别的原理，但在实际中，接收端接收到的码流是一个贯续的二进制比特流：

在接收端无法确知哪个比特是码字ri的开始。

上述运算是在假设n0和h0h1…hm已知的情况下进行的，但实际上盲识别时n0、k0、m和h0h1…hm都是未知的，因此增加了识别的难度。

但是实际中n0、k0确定了卷积码的码率，常用的编码码率有1/2、1/3、1/4、2/3、3/4、7/8几种，因此n0、k0的可能取值及组合为有限集合。而其中2/3、3/4、7/8的卷积码由1/2卷积码删余得到，且删余矩阵一般采用标准删余格式。

m+1是卷积码的约束长度。由于常用的卷积码解码方法有维特比译码和序列译码等，维特比算法的存储深度由约束长度决定，当m<10时有较大的吸引力。当约束长度较大时，一般采用其他译码方式，但由于受译码速度等的约束，m通常也不会太大，而且卷积码的构造没有固定的构造方法，基本上用试凑法或计算机搜索求得，因此其取值有基本固定的选择范围。如文献[7]给出了性能适用于Viterbi译码的可用非系统卷积码及基本生成矩阵[2]，可用以建立取值集合。

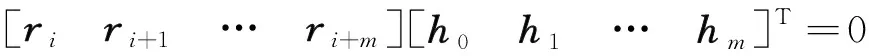
考虑到信号在传输过程中可能引入一定的误码，识别时可增大需要利用的接收码流数量，同时根据传输质量和对误码率预估设定一个校验通过率门限。当确定了一个码字的起始比特后，沿码流以n0为步进依次进行计算，统计计算结果的非零比例与设定的门限比较，当统计结果小于门限时则可以确定卷积码及其参数。

识别的处理流程如下：

① 建立n0、k0和m的元素集合；

② 建立常用卷积码的校验矩阵的先验数据库，实际中只须存储卷积码的基本校验矩阵构成的有限向量h0h1…hm；

③ 取其中一种可能的n0、k0、m和h0h1…hm；

⑥ 重复步骤④～⑤；

⑦ 计算校验通过率，并判断是否大于门限值；

⑧ 如大于门限值则确定接收的编码方式，且序列的起始比特即是码字的开始比特；

⑨ 如校验通过率小于门限值，则滑动窗最初的起始比特沿序列后移1 bit，重复步骤⑤～⑧；

⑩ 如滑动窗最初的起始比特沿序列后移n0后仍未识别出，则重复步骤③～⑩。

3 仿真实验

为了验证本文提出方法的可行性与性能，采用随机二进制信息序列，分别采用表1所列4种编码方式进行非系统卷积码编码，对编码后数据引入随机分布误码模拟信道传输中产生的差错。编码后数据引入误码取值范围为0.1%～1%，利用表1所列4种编码对应的校验矩阵[10]对存在不同误码率的编码数据进行校验，分别进行100 000次校验试验，试验结果如图1所示。

图1 识别性能仿真结果Fig.1 Recognition performance test results

由图1可知，随着误码率增加，校验通过概率会随之降低。对未删余的非系统卷积码，在1%误码条件下有90%以上的校验通过率，对删余的卷积码，能在大部分条件下满足80%以上的校验通过率，仅7/8卷积码在高误码率时低于80%，因此验证该算法能够对各种不同速率的卷积码完成识别。工程中，根据对不同编码方式校验通过率仿真结果设置门限，可以达到在3‰误码条件下整体识别正确率优于90%的识别性能。

4 结论

本文分析了卷积码的校验矩阵和编码序列的关系，针对非系统卷积码，提出了利用常用编码方式的校验矩阵对接收解调码流进行校验验证，从而判定非系统卷积码识别的方法，并用该方法对多种不同速率的卷积码识别性能进行了仿真试验，验证了方法的有效性，给出了该方法的识别性能。该方法运算量小，适于工程中实现和应用。