基于生成对抗网络的密钥生成方法及其在微光图像加密中的应用

2022-05-22李锦青刘泽飞满振龙

兵工学报 2022年2期

李锦青 ,刘泽飞 ,满振龙

(1.长春理工大学计算机科学技术学院,吉林长春 130022;2.吉林省网络与信息安全重点实验室,吉林长春 130022)

0 引言

图像因其信息量大、传输方便等特点,在互联网中得到了广泛应用。光学信息系统由于具有并行处理信息的特点,其在海量信息处理方面展现了数字信息系统无可比拟的优势,特别是处理的图像越复杂、信息量越大,这种优势就越明显。夜视技术就是利用微光和红外线这两个条件,把来自目标的人眼不可见的微光或红外光信息经过信号传感、采集、处理和显示等技术转换为人眼可以感受的可见光[1-2]。其中微光电视、微光夜视仪在对敌固定目标的监视以及对我方重要目标的警戒和安全保卫工作中,都发挥着重要作用[3-4]。但由于微光图像中包含了公安、军事、空间技术等关键信息,保护微光图像免遭恶意攻击逐渐凸显出其重要性,微光图像加密技术受到了国际学术界的广泛关注。此外,不同于可见光图像,微光图像中噪声复杂,纹理特性模糊,光照不均匀,具有信噪比低、灰度等级少等显著特征。传统的可见光图像加密技术直接利用混沌系统产生的随机序列进行加密,这种方式在安全性方面存在不足。随着研究的深入,光学变换的线性关系所带来的安全隐患也逐渐暴露出来。

混沌系统对初值和控制参数具有高度敏感、遍历性、伪随机性和不可预测性,因此在图像加密中得到了广泛应用[5]。混沌系统的非线性特性可以有效地抵消光学加密中线性变换带来的安全风险。然而,部分基于混沌的加密方案常存在一些不足[6-7],例如计算机的有限精度造成较短的周期长度,是混沌密钥流产生器的重要问题之一[8]。为了解决密钥的随机性和安全性问题,研究者们提出了许多关于混沌系统或各种其他技术的密钥生成方案[9-10]。

随着人工智能技术的飞速发展,深度学习已广泛应用于信息安全的各个领域。人工智能时代的图像信息安全越来越受到研究者的关注[11]。自2014 年首次提出生成对抗网络(GAN)以来[12],GAN 已成为计算机视觉[13]、自然语言处理[14]和恶意攻击检测[15]等领域的热门话题。由于GAN 训练结果的随机性和差异性,本文将混沌序列作为训练集和控制生成器,获得比混沌序列具有更多随机性的数据样本,避免了高维混沌系统迭代周期长、耗时等问题。可以得到比混沌序列具有更多随机性的数据样本,同时加快了密钥的生成速度,为微光图像批量加密节省了时间,能够满足实时处理包含重要军事机密等信息的微光图像的需求。

本文的主要贡献如下。

1)首次将量子细胞神经网络(QCNN)产生的超混沌序列作为GAN 的训练集,设计了一种快速随机密钥生成方法。

2)提出了一种与明文相关的二维指针计算方法,以获得与明文相关的随机相位掩模。

3)设计了一种基于GAN 的微光图像加密算法,实现了微光图像的快速安全加密。

1 GAN 密钥生成方法

密钥的随机性已成为影响密码系统安全性的重要因素。GAN 是一类用于无监督机器学习的人工智能算法,它由两个神经网络组成,在一个零和博弈框架中相互竞争[14]。

式中:G为生成网络;D为鉴别网络;v(G,D)为损失函数;x为训练集;Ex～pd为实际输入数据的分布;lgD(x)为鉴别器的判断值,D(x)为D网络模型,用来确定实际数据和训练z是否是输入G网络模型的噪声;Ez～pz(z)为噪声数据的分布;lg(1 -D(G(z)))为生成数据的判断值,G(z)为G网络模型生成的数据。通过最大值和最小值的连续博弈,对G网络模型和D网络模型进行循环交替优化,直到两个模型达到纳什均衡。

量子点和量子细胞自动机是通过库仑相互作用传输信息的新型纳米电子设备[16]。与传统技术相比,量子元胞自动机具有超高集成度、超低功耗、无引线集成等优点。近年来,国内外学者利用细胞神经网络和量子细胞自动机的结构,在薛定谔方程的基础上构建了QCNN。由于量子点之间的量子相互作用,QCNN 可以从每个量子元胞自动机的极化率和量子相位中获得复杂的线性动力学特性,用来构造纳米级超混沌振荡器。对于耦合两个单元的QCNN,可以用以下微分方程来描述:

式中:g1、g2为极化率;h1、h2为量子相位;a1、a2为每个单元中点之间能量的比例系数;b1、b2为相邻单元极化率差异的加权影响因子。当a1=a2=0.28、b1=0.7、b2=0.3 时,系统处于混沌状态。

由于QCNN 是一个高阶超混沌系统,迭代速度较慢,计算量大。将QCNN 产生的超混沌随机矩阵作为GAN 的训练集输入到GAN 中,学习生成随机数据作为加密系统的安全GAN 密钥池。训练后生成的随机数与混沌系统生成的随机数具有类似的特征,即新的随机数同样具有混沌特性。例如随机性和敏感性,在3.1 节中通过NIST 测试检验了其随机性,敏感性表现为当由QCNN 以不同初值或控制参数生成的不同混沌随机序列作为学习对象时,GAN同样也会学习并生成完全不同的随机数。但是GAN 生成的随机数也存在着与混沌系统不相同的特征,如由于学习和训练过程是非监督的,生成的随机数列不受人为控制,即具有不可复现性。总之,GAN 密钥生成方法在保证密钥特性的前提下有效地提高了密钥生成速度。

2 微光图像加密算法

将GAN 密钥生成方法应用到新的微光图像加密算法中,并设计了一种与明文相关的二维坐标指针计算方法,在每次加密时,都会从密钥池中利用明文相关控制参数与用户设定的参数计算出一个特定的位置,然后从密钥中获取不同的随机序列作为置乱密钥。本文算法描述中仅给出了一个置乱加密框架,但实际每次置乱操作都是设定与明文和用户均相关的不同操作,攻击者无法通过已知明文或选择明文攻击来攻破该加密算法。

混沌系统生成的密钥经过GAN 训练后,得到GAN 密钥池,从GAN 密钥池中选择两个混沌随机相位掩膜用于扩散阶段。加密整体过程如图1 所示,RM1和RM2为两个相位掩膜。原始图像先经过了置乱,随后进行双随机相位分数傅里叶变化(FFT),从而得到最终的密文图像。

图1 加密流程图Fig.1 Encryption flowchart

加密具体步骤如下:

步骤1选择一个大小为M×N的明文图像,像素矩阵为P。

步骤2通过迭代混沌系统(2)式生成伪随机序列H1、H2、H3、H4,并将其作为GAN 的训练集。训练后,可以得到完全随机的密钥池Kr(密钥的随机性测试见3.1 节)。

式中:GAN(·)为生成对抗网络模型函数,如(2)式所示。

步骤3从明文图像P中计算与明文相关的二维指针,如(4)式:

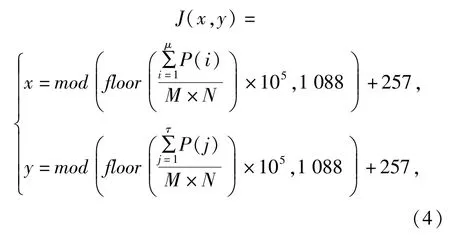
式中:x、y为指针对应的横坐标和纵坐标;J(x,y)为明文相关的二维指针;μ、τ为用户控制参数,均取值80;P(i)为像素值;mod(·)为取余函数;floor(·)为向下取整函数。

步骤4通过使用明文相关指针J(x,y),从密钥池Kr中选择两个相位掩膜RM1和RM2,生成方法如图2 所示。图2 中,x1、y1为另一对明文相关指针J(x1,y1)对应的坐标。

图2 明文相关二维指针选相掩模方法原理图Fig.2 Schematic diagram of phase selection mask method for plaintext correlation 2D-pointer

步骤5通过混沌指针从密钥池中选取M×N大小的随机序列,由小到大进行排序,得到索引矩阵I,对明文图像进行排序置乱,得到矩阵Ps。

式中:sort(·)为对l进行排序的函数;reshape(·)为矩阵变形函数;Pg为生成的置乱图像。

步骤6对置乱图像Pg进行光学双随机相位分数傅里叶变换加密,以获得最终的加密图像。

加密流程结束,由于本文提出的加密方案为对称加密,其解密过程即为整个加密过程的逆过程。

3 性能安全分析

选取256 ×256 大小的明文图像“树”和“鹿”作为测试对象,图3 给出了该加密方案的加密或解密实验结果。

图3 实验结果Fig.3 Experimental results

3.1 GAN 密钥池的随机性分析

使用NIST 测试评估密钥池中整体密钥的随机性。表1 列出了密钥的NIST 测试结果。由表1 可见:GAN 密钥生成方案能够通过所有的NIST 测试(共16 种测试项),每个测试都有一个测试结果;P为检验序列分布均性的指标,如果P值大于0.01,则测试成功,表明该密钥生成方法所生成的随机密钥从近似熵、离散傅里叶变换、频率、线性复杂度等多角度符合随机性要求。

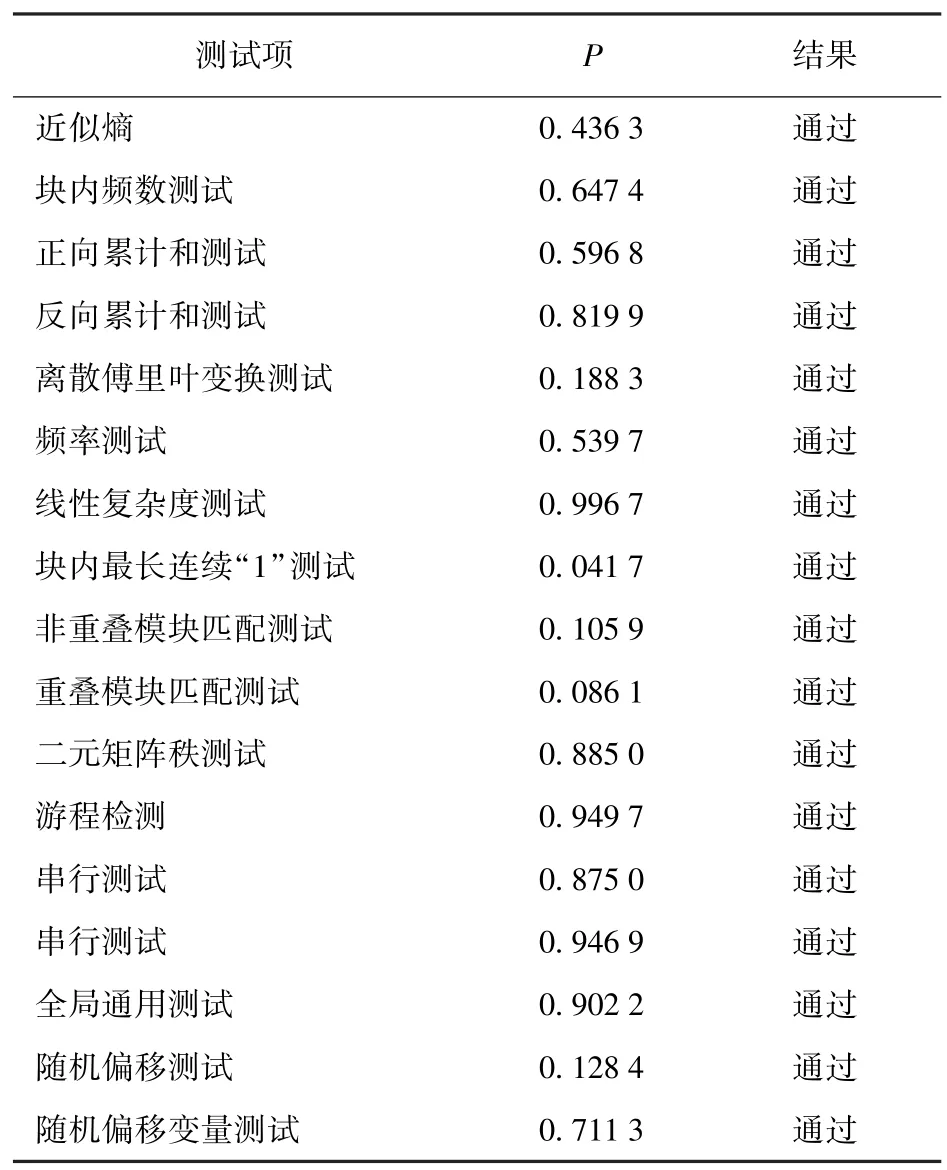
表1 NIST 测试Tab.1 NIST test

3.2 密钥空间分析

密钥空间是衡量加密系统抵抗暴力攻击的重要指标。理想的图像加密算法应具有大于2100的密钥空间,以提供高安全性[17]。加密方案使用QCNN 的4 个初始值和4 个控制参数作为加密和解密密钥。因为初始密钥的每个精度是10-16,所以密钥空间为(1016)8＞2384。因此,密钥空间达到了安全标准,能够抵抗各种暴力攻击。

3.3 直方图分析

图4 所示直方图反映了图像灰度分布的统计特征。从图4 中可以看出,加密图像直方图的像素分布是平坦均匀的,类似于白噪声,可以很好地隐藏明文图像的灰度信息,从而有效地抵抗统计分析攻击。

图4 直方图分析Fig.4 Histogram analysis

3.4 相邻像素相关性分析

一个优秀的加密算法可以很好地破坏明文图像相邻像素之间的相关性,该相关性可由相关系数定量描述。图5 和图6 分别给出了两幅明文图像和密文图像的像素分布。从图5 和图6 中可以看出,明文图像的相邻两个像素通常具有很强的相关性,而加密图像中的像素分布更均匀,扩散性更好,有效地破坏了平面图像的相邻像素相关性。

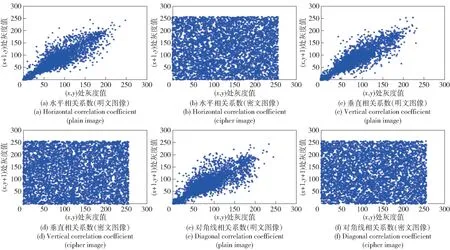
图5 树的明文图像和密文图像的像素相关性分析Fig.5 Correlation analysis between plain image and cipher image of trees

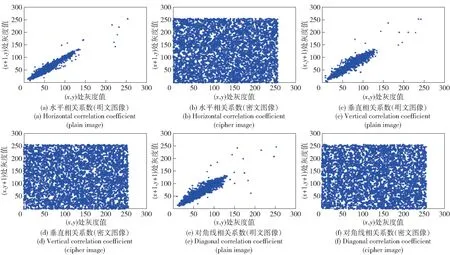
图6 鹿的明文图像和密文图像的像素相关性分析Fig.6 Correlation analysis between plain image and cipher image of deer

本文同时计算了原始图像和密文图像在水平、垂直和对角线方向上的相关系数,计算结果见表2。由表2 可见,密文图像的相关系数趋于0,与其他同类算法[18-20]相比,本文加密方案更高地隐藏了相邻像素之间的关系。

表2 明文图像和加密图像的相关系数Tab.2 Correlation coefficients of plain images and cipher images

3.5 信息熵分析

信息熵反映了图像中每个灰度值或亮度值的均匀性。对于8 位灰度图像,理想的信息熵应该是8。

当信息熵越接近8 时,图像携带的确定性信息越小,信息越接近随机噪声,加密性能越好。其熵值H(m)可通过(7)式计算:

式中:mi为第i个像素值;N为符号mi∈m的总数;p(mi)为符号mi出现的概率。表3 列出了密文图像的信息熵结果。由表3 可知,与文献[19 -21]中的算法相比,该方案在信息熵方面有更好的表现,并且加密图像的像素分布更具随机性。

表3 密文图像信息熵Tab.3 Information entropy for cipher image

3.6 差分攻击分析

差分攻击分析的目的是分析明文图像细微变化引起的密码图像变化程度,密码图像变化程度越大,加密系统的图像敏感度越强。本文通过像素数变化率(NPCR)和统一平均变化强度(UACI)计算加密算法对明文的敏感度。NPCR 和UACI 定义分别为

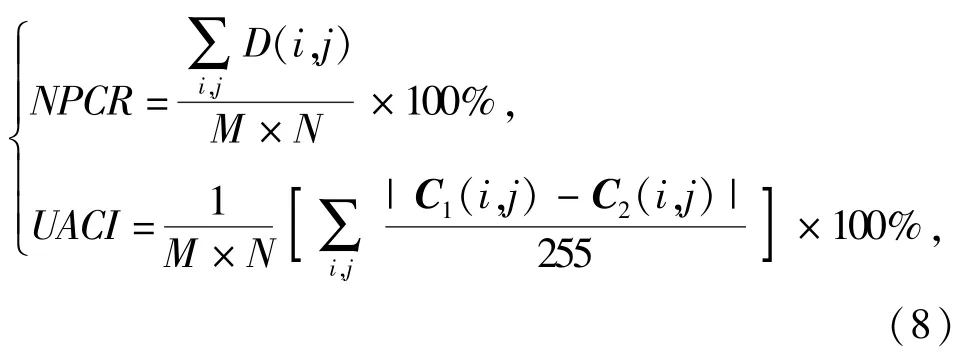
式中:i、j为图像中像素值的位置;C1、C2分别为两个密文图像,

由(8)式可知,NPCR 越接近理论值99.609 4%,UACI 越接近理论值33.463 5%,说明抵抗差分攻击的能力越强。表4 列出了本文方案NPCR 与UACI的计算结果,及其与其他同类算法的对比[19,21-22]。可见本文方案的实验结果与理想值非常接近。

表4 NPCR 和UACI 值Tab.4 NPCR and UACI values

3.7 速度性能分析

除了加密算法的安全性以外,加密速度也是实际应用过程中的一项重要指标。本文提出的方案在MATLAB 2015b 平台,配置为Intel(R)Core(TM)i7-6500U @2.50 GHz 处理器,8.00 GB 内存的个人计算机中完成。表5 列出了使用本文算法对两幅原始微光图像“树”和“鹿”进行加密所需的时间。由表5 可以看出,与其他加密算法相比[23-25],本文提出的算法满足快速加密的需求。