课堂教学中培养小学生数学语言表达能力的策略

顾万全

（江苏省淮安市淮海小学教育集团）

数学语言表达能力作为《义务教育数学课程标准（2011年版）》规定的教学培养目标之一，一直被数学教师所重视。培养学生的数学语言表达能力，要求在理解数学知识的基础上，用简洁而精确地的语言表达数学含义。课堂中，教师应该在传授知识点的同时提升学生的数学学语言表达能力，从关键词入手，引导学生掌握多种表达形式，做到正确理解、转换及规范表达。

一、抓住关键词，规范专业用语

数学语言表达要求准确和简洁，课堂中，教师要抓住数学语言表达的关键词，规范专业用语，使学生学会用准确和简洁的数学语言进行表达。在课堂中，部分学生陷入表达困境是因为数学语言的匮乏，对数学知识理解了，但无法用准确地数学语言表达出来。这时，就需要教师有针对性地加以规范，给出正确的表达方式，帮助学生掌握数学关键词，进而学会表达。

在教学人教版《义务教育教科书·数学》五年级下册第三单元“长方体与正方体”时，教师先要帮助学生建立长方体和正方体的概念，并对其组成特征进行分析。在这一过程中就涉及到了对长方体特征的描述，教师要引导学生对长方体模型进行观察和感知，并说出它是由几个面围成的。当学生回答出“6 个面”时，教师应继续补充：“的确是6 个面，但是这句话如何表达得更完整呢？”有学生回答：“长方体是由6 个面组成的”。针对表达中的“组成”二字，教师可引导学生展开探究：试分析一下由6 个面组成的还可以有什么图形？经过实际探究学生发现，许多物体都可以由6 个面组成，比如可以拼一个六角形围栏，还可以搭成一座小桥。这样，学生就发现了前面表达中存在的不准确现象：长方体确实是由6个面组成的，但是6 个面组成的物体并不一定是长方体。此时，让学生思考最开始提问时教师所用的词语，学生终于发现了“围成”这一关键词，进而得到了规范的数学语言表达：长方体是由6 个面围成的立体图形。

在数学语言表达中，关键词具有十分重要的作用，一个关键词使用不当就有可能使表达产生歧义或者误解。因此，教师要鼓励学生大胆表达，并针对学生表达中出现的不规范或不够专业的词语进行纠正，引导学生学会抓住数学语言表达中的关键词，提升其数学语言表达能力。

二、基于知识本质，强化表达形式

数学语言表达有多种形式，各种表达形式之间在很多情况下可以互换互通。教学中，基于不同知识本质，选择不同的数学语言表达形式，有助于学生对知识进行准确表达和直观理解，对于发展学生的数学思维有着不同的促进作用。因此，教师应引导学生对适用于不同数学知识本质的语言表达方式进行探究，强化多种数学语言表达形式，发展数学思维能力。

（一）发展形象思维，用图形语言表达

图形语言是形象思维的良好载体，用图形语言表达，可以将抽象的数学概念含义和信息转换为直观可见的图形，有助于学生借助形象思维直观地理解数学含义，发现问题当中的主要信息，分析并解决问题。因此，教师要注重图形语言表达能力的培养，抓住学生形象思维发展的黄金时期，提高学生的数学形象思维能力。

在教学“梯形的面积”一课时，我先出示一个梯形的直观示例，并给出梯形的上、下底以及高的长度，让学生结合平行四边形面积的求法计算梯形面积的大小。有的学生联想到在推导平行四边形面积公式时，要对平行四边形进行切割和平移，将其转换为长方形之后进行求解，进而思考：梯形是否也可以被切割重组为一个已经学过的简单图形呢？我鼓励学生在演算纸上通过图形语言表达，直观地尝试表达出对梯形进行切割重组的过程。通过探究学生发现，该梯形可以通过延长上底左侧到下底右侧进行切割得到两个三角形，这两个三角形的高大小相等，而底边则分别为原梯形的上、下底。所以，梯形的面积可以由切割后的两个三角形面积的大小相加求得。这样，就得到了梯形面积计算的图形语言表达，再通过三角形面积公式就可以计算得出原梯形的面积为b×h÷2+a×h÷2=（a+b）×h÷2。其中，a、b分别为梯形的上、下底，h为高，从而得出了梯形面积的计算方法。

在求解多边形面积公式时，通过图形化的表达语言，可直观地展示在推导复杂图形面积时所用到的图形转化思想，通过割补方案，利用已有公式的简单图形表示出未知图形的面积求法。这样，不但可以促进学生创新能力的提升，而且能够强化图形语言表达能力，提高形象思维能力。

（二）发展抽象思维，用符号语言表达

符号语言是数学学科中应用最广泛的一种表达方式，是数学学科抽象性的重要体现。符号语言具有抽象性和简洁性的表达特点，其通过将数学问题抽象化从而把复杂的问题抽象为间接的符号表达，以便于理解和表述。课堂教学中，教师要注重对学生符号语言表达能力的培养，要在锻炼学生数学逻辑思维能力的同时发展其抽象思维能力。

在教学“乘法分配律”一课的相关内容时，我引导学生在理解运算原理的基础上，基于符号语言对运算原理进行表述。先通过一个实际问题的求解让学生理解乘法分配率的运算原理：某位同学在商店购买了两支铅笔和两个橡皮，其中铅笔单价1.5 元，橡皮单价1 元，该同学总共花了多少钱？根据所学的四则运算公式，学生认为总的花费等于铅笔的总价加上橡皮的总价，即1.5×2+1×2=3+2=5 元。然后，我追问：“在计算这个算式的时候有没有发现什么规律呢？用2.5×2这个算式算出来的结果与原式计算得出结果有什么关系？”通过对第二个算式进行计算学生发现，两者得出的结果相同，进而继续对第一个算式进行分析，发现原式中两个乘法运算的乘数相同，在第二个式子中同样是乘数2，但是第一个因数则变成了原式中两个因数的和，也就是原式=1.5×2+1×2=（1.5+1）×2。最后，我引导学生对这一运算规律进行抽象化表达，利用符号语言表示式中的数字。学生可以得出a×c+b×c=（a+b）×c，从而得出了乘法分配律的符号表达。

符号表达形式是对数学运算过程或者数学概念的高度抽象化表达，教师在课堂中强化学生的数学符号表达能力可以促进学生对数学知识本质的理解。因此，在教学过程中教师要深化对符号语言表达的理解，引导学生顺利完成从形象思维到抽象思维的发展过渡。

三、引导多重转换，实现灵活互译

学生数学语言表达能力强的一个重要体现是多种表达形式之间的互译互通：通过不同表达形式之间的转换快速理解数学概念、分析数学题目以及解决数学问题。因此，教师在教学过程中要有意识地引导学生在不同表达形式之间相互转换，基于数学知识本质建立起不同表达形式之间的联系，有效提升学生的数学语言表达能力。

（一）辨别数量关系，文字与符号语言互译

在利用数学知识解决生活问题时，一个重要方法是辨别出题目中所包含的数量关系，先利用文字语言表述自己的理解和解题过程，之后利用符号语言实现数学计算。其中，文字语言具体形象，便于理解；符号语言简洁明了，方便计算。在教学过程中实现两者的有机融合，对于增强学生分析和解决问题的能力有着十分积极的作用。

在教学“实际问题与方程”这一课时，教师要针对实际问题，引导学生挖掘题目当中所包含的数字关系，并将用文字语言表述的数量关系转换为符号语言（也就是方程式）之后再解决问题。教师可先提出问题：小明在运动会跳远项目中取得了3.68 米的好成绩，打破了学校的跳远纪录，已知这个新纪录超出原纪录0.08 米，请问原纪录是多少米？在这个问题中，要引导学生挖掘题目中包含的表征数量关系的词语，辨别其中蕴含的数量关系，然后结合题目中给出的数据和数量关系设未知数进行求解。通过对问题进行分析学生可发现，题目中包含的“超出”二字蕴含数据量大小之间的关系，结合上下文可以分析得出，原纪录比新纪录小0.08米，也就是原纪录加上0.08 米等于新纪录3.68 米。接着，教师可让学生尝试将这一文字语言表述转换为方程的符号语言表达形式，即把原纪录设为未知数x，那么利用符号语言表达形式表示这一数量关系可以得出x+0.08=3.68，从而借助数量关系实现了符号语言和文字语言之间的转换。最后，学生可利用小数减法3.68-0.08=3.6计算得出原跳远纪录长度为3.6米。

符号与文字语言表达之间的转换是方程思想的直接体现，教师要引导学生结合实际问题，对文字语言和符号语言进行互译转换，这样可以提高学生分析和解决实际问题的能力，强化学生对于数学符号语言表达抽象性的感悟。因此，教师在课堂教学中要有针对性地引导学生对数量关系进行辨别，基于数量关系实现符号语言和文字语言之间的表达和转换。

（二）图解概念内涵，图形与文字语言互译

在数学学科中，许多数学概念和内涵都是通过文字形式来表达的，小学阶段学生的认知特点是以形象思维为主，因此学生很难对这些基于文字语言描述的抽象数学概念有直观的理解。所以在小学数学教学中，要充分利用图形语言直观形象的优势，图解概念内涵与冗长的文字描述，进行等量互译，以便学生能直观地理解数学知识点。

在教学“正比例”一课时，我结合一组具有正比例特点的数据例子，引导学生自主探究，利用图形的形式描述出数字之间的关系，并通过观察，绘制出图形，对正比例的概念和含义进行总结。我先提出问题：某造纸厂每天对生产出的纸张数量进行统计，发现在第1、2、3、4、5 天内生产的量分别为70、140、210、280、350吨，请分析该工厂的生产量和生产天数之间有什么关系？（如表1）

表1 生产量与生产天数关系

学生试着用图形语言的方式进行表述。我引导学生将该组数据放在表格中进行图形语言表达，表格中每行的一个格子代表一天，而每一列的一个格子代表70 吨的产量，按照给出的数据将在不同天数所对应的生产量吨数在表格中画圈标出，之后将所有的圈连起来就完成了这一组数据的图形语言表达（如图1）。

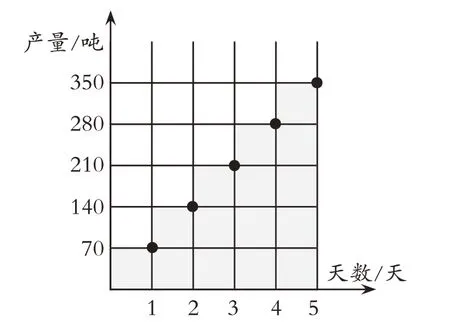
图1

通过观察图形学生发现，他们绘制出的是一条直线，该直线上每一个点都代表相应的生产天数，每一列的数值则表示在对应生产天数下的总产量。这样，他们就获得了对于正比例概念的图形显示，观察出两个相关联的量呈直线发展。

通过图形语言与文字语言的互译转换，学生更加直观地分析出了正比例的数学概念。因此，教师要充分考虑到学生在小学阶段以形象思维为主的认知特点，在课堂教学中引导学生利用图形语言对教材中的文字概念进行表述，在表达形式互换的过程中帮助学生获得对数学概念的理解，提高数学图形语言表达能力。

（三）描述变化过程，符号与图形语言互译

基于抽象思维的数学符号语言表达形式对于提升学生的逻辑思维能力和抽象思维能力有着十分重要的意义。符号语言表达能力的培养应该以图形语言为基础，用符号语言对图形当中的变化过程进行描述，实现由形象思维到抽象思维的过渡，助力学生顺理成章地得到符号语言表达形式，促进学生对数学知识本质的理解。

在“圆柱的表面积”一课的教学中，我要求学生掌握圆柱体表面积公式的推导方法，并能够灵活运用。对于这一几何类问题，教师要利用图形的变换过程引导学生通过直观观察来得到圆柱体表面积的构成。教师可通过多媒体设备进行动画演示，给出圆柱体的展开过程，引导学生发现，圆柱体表面积实际上是由两个底面和一个侧面组成的，将侧面沿一条高进一步展开之后可以得到一个长方形。根据图形变换过程学生可以知道，圆柱体的表面积就是展开后三个图形的面积之和。教师再引导学生探究展开后的两个圆形以及一个长方形与展开前圆柱特征之间的数量关系。学生会发现，得到的两个圆形面积与圆柱的上、下底面积完全相同，而最后展开的长方形的长和宽分别为之前圆柱的底面周长和高。根据“圆柱展开后总的面积保持不变”这一原理，学生将上述展开过程中的图形变换转换为数学符号语言，得出计算公式S圆柱=2×S底面+S侧面=2×πr2+2πr×h，其中r为上、下底面圆的半径，h为圆柱的高。

数学图形语言是学生最容易接受和理解的一种表达方式，教师要基于这一特点，引导学生开展图形语言与数学符号语言之间的相互转换。在课堂教学中教师要给予学生图形变换实践操作的机会，使他们在动手实验中探究图形变换中所蕴含的数学变量关系，尝试用符号语言表示图形的变换过程，从而顺利地抽象出符号语言表达形式。

综上所述，培养学生的数学语言表达能力要注重课堂教学过程中的数学表达，引导学生探析数学语言构成成分，发现数学表达中的关键词。要基于数学知识本质，探究不同数学表达形式之间的相互转化关系，通过长期的积累，逐渐提高学生的数学语言表达能力。