再生核Hilbert空间中两阶段稀疏表示目标跟踪算法
2022-05-21朱虎飞丁子豪杨永亮冯旭祥丁大伟
朱虎飞 ,丁子豪 ,杨永亮 ,冯旭祥 ,丁大伟
(1.北京科技大学自动化学院,北京 100083;2.北京理工大学自动化学院,北京 100081;3.中国科学院空天信息创新研究院,北京 100094)
1 引言
目标跟踪是计算机视觉研究领域的热点之一,目标跟踪往往由于复杂的背景图像和目标的运动状态的随机性和不确定性,导致精确的检测与目标跟踪成为一项非常困难的工作[1].鲁棒的跟踪算法在出现环境以及目标外观发生改变的情况下,算法仍然能保持较好的跟踪精度[2-3],如何对目标的外观建模是鲁棒跟踪的关键[4].判别方法和生成方法是当前目标跟踪技术中的使用的两种主要方法[5].判别方法[6-8]将跟踪任务建模为基于二分类器的检测问题,将目标对象与背景进行分离.生成方法[9-11]一般先对目标的外观进行学习获得目标表示模型,然后搜索与该模型最相似的图像区域作为跟踪目标.基于稀疏表示的生成式模型所携带的目标信息更丰富,相比于其他方法能较好的处理视角变化和部分遮挡等问题[11].
近年来,稀疏表示(sparse representation,SR)作为一种高效工具广泛应用于分类[12]、视觉跟踪[11]和人脸识别[13]等领域.Mei和Ling将稀疏表示首次应用至目标跟踪领域,提出了L1目标跟踪器[11],在此基础上研究者们又提出了几种改进的基于稀疏表示的目标跟踪算法.Jia[14]和Wang[15]利用目标的局部信息和空间信息,提出了局部稀疏表示模型.Bao等针对L1跟踪器,添加了关于琐碎模板相关系数的L2范数正则项,从而提高了跟踪精度[16].但是,以上方法都是在数据的原始空间上建立线性稀疏表示模型,而没有考虑到目标形变等其他复杂特性.核方法作为一种非参数化方法,在描述特征空间中数据的非线性关系时,可以有效改善参数化方法的局限[17].因此,Gao等为了捕获图像样本与字典之间的非线性信息,减少特征量化误差,提出了一种核稀疏表示(kernel sparse representation,KSR)方法,并成功应用于图像分类与人脸识别[18].在传统稀疏表示算法中,通常为了检测遮挡而引入琐碎模板.然而琐碎模板的选择主要依赖人工经验,并且会对目标跟踪效果产生较大影响.为了避免琐碎模板的引入,Wang等将核稀疏表示应用在了目标跟踪领域[19].
针对目标跟踪中出现的视觉漂移问题,Wang提出了一种基于局部稀疏表示的两阶段算法,第1阶段使用自适应观测模型来估计初始跟踪结果[15].第2阶段使用静态观测模型来确定最终的跟踪结果.在此基础上,Yan[20]又提出了一种基于核稀疏表示的两阶段算法,并根据在线学习得到的分类器来区分目标和背景.第1阶段利用整体信息估计初始跟踪位置,第2阶段利用局部信息确定最终跟踪目标.但由于Wang和Yan采用的都是判别式的跟踪算法,计算量大,难以满足目标跟踪中实时性的要求.
针对稀疏表示模型的求解,Mei使用了琐碎模板加L1范数最小化求解跟踪目标[11];Xu[21]等人提出了一种L1/2范数最小化方法求解稀疏表示模型,该方法通过迭代的求解L1范数最小化问题实现,另外,使用L1,2也可以得到稀疏表示模型[22-23],而一般情况下单独使用L2范数无法获得稀疏模型.对于核稀疏表示模型,Wang[19]使用了特征空间的L1范数最小化求解核稀疏模型,并提出了基于核的坐标下降法求解最小化问题,但计算量大.
不同于上述工作,本文提出了一种新的基于核的两阶段稀疏表示(two-stage sparse representation,TSSR)目标跟踪算法,基于粒子滤波框架和两阶段稀疏逼近描述,研究了视角变化以及部分遮挡等因素存在下的目标跟踪问题.在第1阶段利用图像样本与字典在原始空间中表示模型估计初始跟踪位置,在第2阶段使用核方法将原始空间映射到高维特征空间(再生核希尔伯特空间),利用核稀疏表示模型求解图像样本与字典之间的非线性关系来确定最终的跟踪目标.同时提出了一种基于核方法的加速近端梯度算法求解特征空间中的范数最小化问题,并通过实验证明了算法的有效性.
2 问题描述
目标跟踪问题通常针对如下系统:
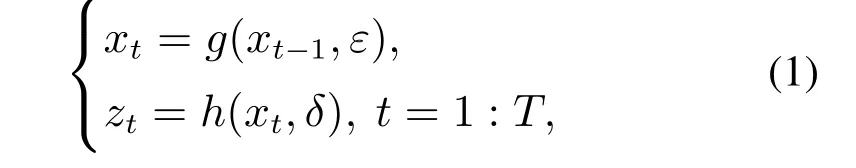
其中:xt−1,xt分别表示第t-1和t时刻跟踪目标的状态,即目标的位置和大小;zt表示从第t时刻目标状态的观测值;ε和δ分别表示系统中的状态转移噪声和观测噪声.
2.1 粒子滤波

但在实际中p(xt|z1:t)可能是未知的,无法直接采样得到有效粒子,通常需要借助重要性采样(sequential importance sampling,SIS)算法.从一个已知的且容易采样的分布q(xt|x1:t−1,zt)中抽样得到粒子,同时粒子的权值更新公式为
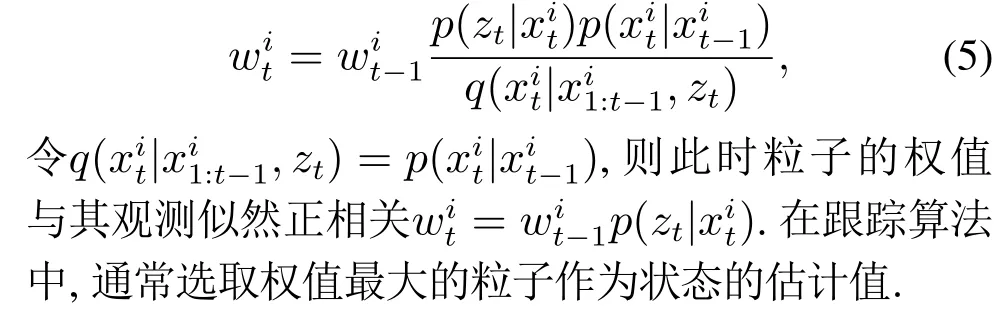
3 稀疏表示
在传统的稀疏表示算法中,将视频图像序列中前几帧包含跟踪目标的人工标注图像区域作为训练集,通过该训练集可以得到由m个模板元素组成的字典D=[d1d2··· dm]∈Rl×m,其中l为模板元素的维数.一个经过向量化处理过的图像样本y ∈Rl×1可以通过字典进行稀疏表示

其中:c=[c1c2··· cm]T∈Rm×1是系数向量,ε表示误差向量.在粒子滤波框架下,式(6)的稀疏表示系数通常通过求解以下L1正则优化问题来得到,即
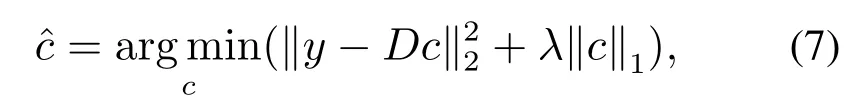
其中λ是一个平衡参数,用于调节正则化的强度.
3.1 两阶段稀疏表示方法
本文提出了一种两阶段的稀疏表示方法,在第1阶段中利用图像样本与字典在原始空间中的线性关系估计初始目标位置,第2阶段利用图像样本与字典在特征空间中的非线性关系确定最终的跟踪位置.该方法的理论框架如图1所示.

图1 两阶段的稀疏表示方法Fig.1 Two-stage sparse representation
3.2 第1阶段:原始空间表示模型
在第1阶段建立图像样本与字典在低维原始空间中的线性表示模型,即式(6).并使用批处理最小二乘方法计算该模型的表示系数c0,即

同时,本文选择高斯函数来设计粒子在原始空间中观测似然,即

3.3 第2阶段:核稀疏表示
本文利用两阶段的核稀疏表示,首先将候选目标被表示为目标模板的线性和非线性组合,然后选取模板重构误差最小的候选目标作为跟踪目标,主要基于以下两点考虑:
1) 稀疏表示模型中的琐碎模板可以有效解决部分遮挡问题[11],琐碎模板的引入给稀疏表示模型的求解带来了较大的计算成本.本文利用核方法建立了高维特征空间中的稀疏表示模型,提出了核稀疏表示,并在模板字典中舍弃了琐碎模板,通过特征提取函数,在核稀疏表示模型中引入对视角变化和部分遮挡不敏感的复杂特征来隐式地表示候选目标,从而避免了在模板字典中引入琐碎模板带来的额外计算成本.
2) 传统的表示模型,将图像样本分解为模板字典中少数原始模板线性组合后的特征,并没有利用到图像样本和模板的复杂特征.核方法可以捕获特征的非线性相似性,相比于稀疏表示,核稀疏表示可以学习到更多判别性的稀疏编码[18].核方法将非线性可分离的特征映射到高维特征空间,在高维特征空间中,相同类型的特征更容易组合在一起,并且不同类型的特征变得线性可分离,在这种情况下,可以更容易地找到信号的稀疏表示,也可以减少重构误差.
3.3.1 核方法
本文在第1阶段的原始空间中,利用候选目标之间线性可分离的特征,对粒子进行筛选.在本阶段使用核方法将候选粒子集与字典集映射到高维特征空间,将候选样本分解为模板字典中少数模板非线性组合后的特征.得到基于核的稀疏表示模型
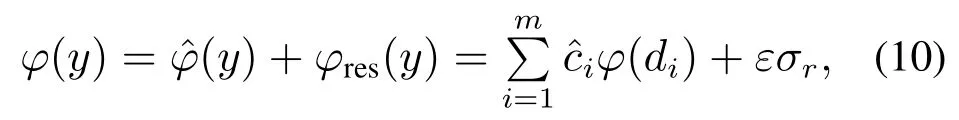
其中:φ(·)表示从低维空间到特征空间的映射,即特征提取函数,φres(y)=εσr为表示残差,且σr是与前m个特征向量φ(di)正交的单位向量.
如图2所示,图2(a)中的红框和蓝框分别框出了精准的和偏差的图像识别结果,图2(c)为模板集中的10个目标模板,图2(b)和图2(d)分别对应精准的和偏差的表示系数.从图2可以看出,精准的图像识别结果对应的表示系数往往是稀疏的,即表示系数向量中只有少量的非零元素,而偏差的图像识别结果对应的系数是非稀疏的.因此,本文通过在求解表示模型过程中添加L1范数惩罚项,控制表示系数的稀疏性.为了防止重构误差过小,出现表示模型过拟合的情况,本文在求解核稀疏表示模型的过程中添加再生核Hilbert空间(reproducing kernel Hilbert space,RKHS)范数用来控制模型的复杂度.在特征空间中,基于核的稀疏表示系数为

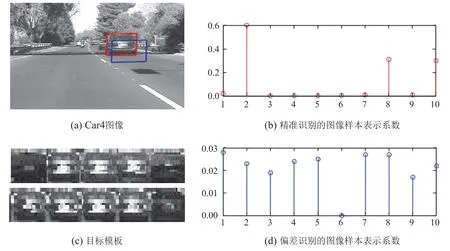
图2 基于目标模板的两种表示方法对比Fig.2 Two representation methods comparison
最后,本文将粒子在原始空间和高维特征空间得到的观测似然相加
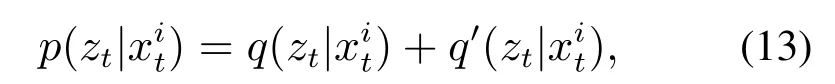
作为图像样本与字典之间的相似性度量,确定最终的跟踪目标.选择字典之间的相似性度量最大的候选粒子作为t时刻的跟踪结果,即
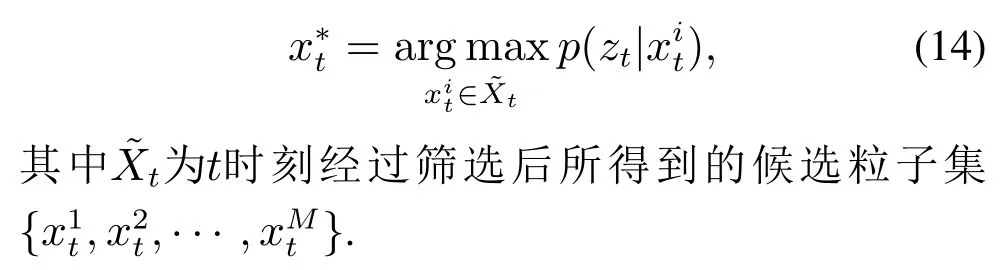
对于式(11)的求解,本文提出了一种新的基于核的加速近端梯度算法,详细推导过程见下一节.
3.3.2 基于核的加速近端梯度算法
对于式(11)中RKHS范数的定义如下:成立.

Mercer定理指出存在一个唯一的再生核Hilbert空间及映射φ(·)与满足上述条件的函数k(x,y)对应.本文利用核稀疏表示学习样本的判别性编码,相比于其他核函数,高斯核函数具有较强的判别能力[24].因此,特征映射之间的内积可以由高斯核函数表示,即
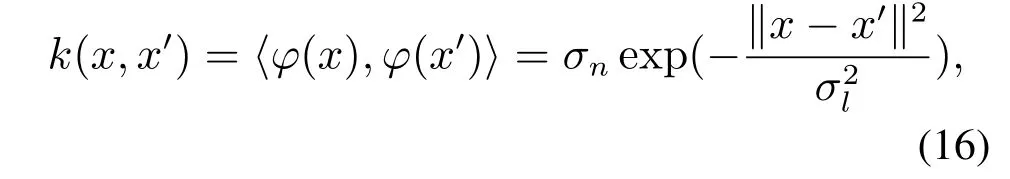
将其带入式(15)得到
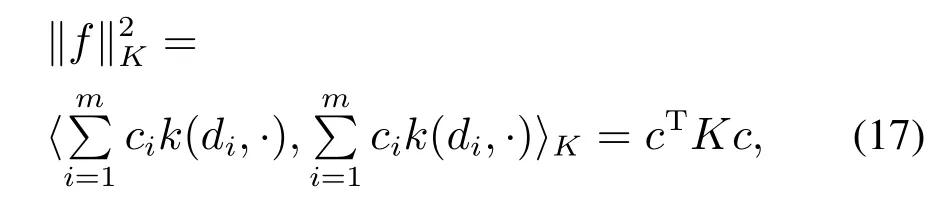
其中K是由核函数生成的核矩阵.接下来,定义F(c)=g(c)+h(c),其中
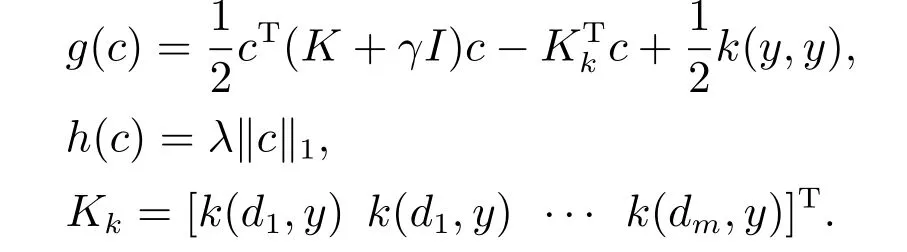
特别地,g(·)是可微凸函数,h(·)是不可微凸函数.其中,g(·)的梯度为
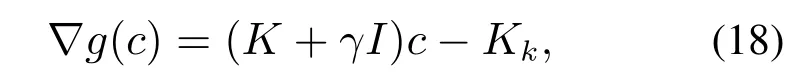
根据文献[25],不可微凸函数h(u)带惩罚因子ρ的邻近算子形式可表示为
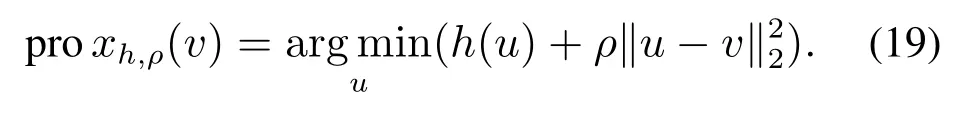
为了简化计算,令ρ=1,定义v=z-η·∇g(z),其中η为步长.由此,核稀疏表示系数的递推公式如下:
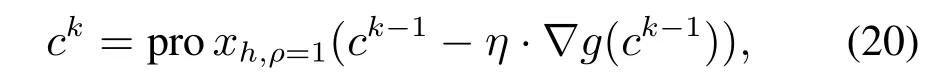
使用软阈值(soft thresholding)方法进行求解可得到
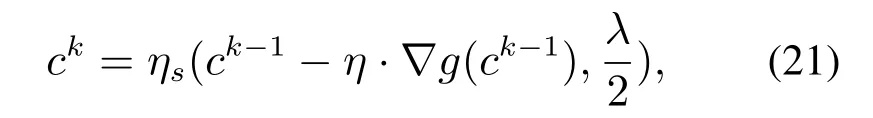
其中ηs(·,·)为软阈值函数,即

sgn(·)为符号函数.为了减少KAPG算法的迭代次数,本文使用了c0作为迭代初值.
综上,本文中使用KAPG算法迭代求解式(11)的伪代码如表1所示.

表1 KAPG求解核稀疏表示Table 1 Solving kernel sparse representation with KAPG
针对加权系数λ和γ,由于它们的信息无法被训练数据集表示,因此本文依靠经验指定加权系数的值,人为地限制函数空间的大小.为此,本文将Car4数据集作为验证集,改变加权系数并进行了多次实验,得到TSSR算法在验证集上的跟踪精度,结果如文中的表2所示,每个表格中的第1行数据为平均中心误差,第2行为平均重叠率.选取λ=0.11和γ=0.11,作为本文算法的超参数.
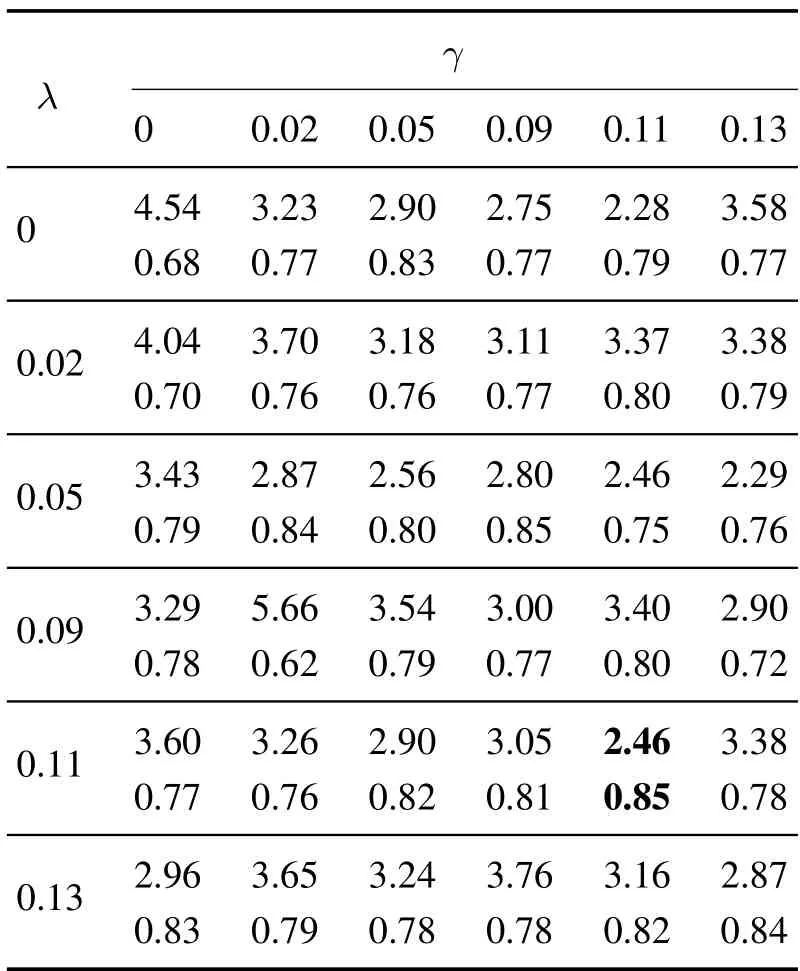
表2 超参数选择Table 2 Hyperparameter selection
4 模板字典更新
在跟踪过程中,为了适应视角变化导致的目标姿态和形状变化,本文提出了在高维特征空间中的模板更新策略,防止跟踪过程发生漂移,在跟踪过程中将跟踪结果作为替代模板加入到字典中.通常认为目标的姿态和形状连续变化,但连续更新模板可能会丢失过去的表观信息,引入过多的噪音,本文通过设立更新阈值的方式来解决这一问题.假设在t时刻的跟踪结果为yt,且yt与模板字典中的第i个模板di的相似度量为

其中的值越大,表明yt与di的相似度越高.
由于字典集中有m个模板,若对每个模板都计算相似性度量,则计算量太大.为此,本文设计第i个模板在t+1时刻对应的贡献度为
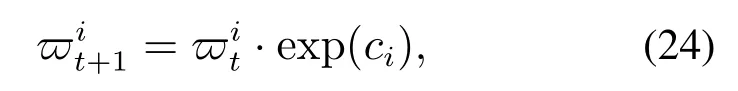
其中:ci表示第i个模板对应的稀疏表示系数,且模板的初始贡献度为=1/m,m为字典中模板的总数.选取在稀疏表示中贡献度最大的模板计算其与跟踪结果yt的相似度量ξ,同时定义模板的更新阈值为τ.当ξ <τ时,用yt替代掉字典中贡献度最低的模板,同时将各模板的贡献度重新设为1/m,否则按式(24)进行贡献度更新.
4.1 两阶段稀疏表示算法框架
本文所提出的再生核Hilbert空间中的TSSR目标跟踪算法在粒子滤波的框架下,使用两阶段的稀疏表示求解粒子的观测似然来确定跟踪目标在每帧图像中的位置和大小信息.其中,在第1阶段稀疏表示算法是在图像样本与字典的低维原始空间求解粒子的观测似然,并根据观测似然对粒子进行筛选得到候选粒子集.第2阶段将候选粒子通过核方法映射到高维特征空间求解候选粒子的观测似然,对粒子进行二次筛选得到最终的结果.并根据当前帧图像的跟踪结果对模板进行更新,提高算法的鲁棒性.综上所述,本文设计目标跟踪算法结构图如图3所示,伪代码如表3所示.
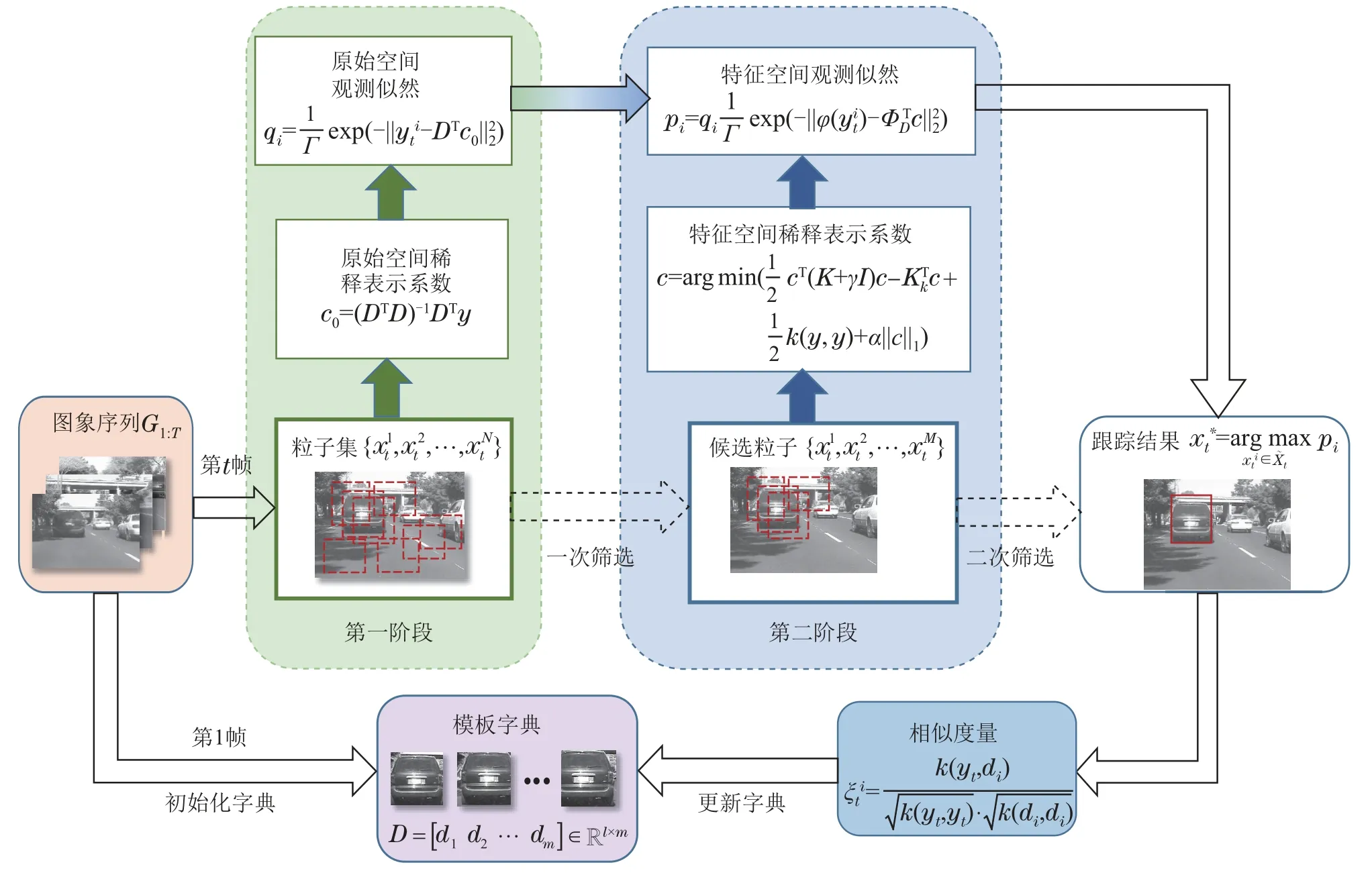
图3 算法流程图Fig.3 Algorithm flow chart

表3 基于核的TSSR目标跟踪算法Table 3 TSSR objective tracking algorithm based on kernel
5 实验结果与分析
为了验证本文所提出的TSSR算法的有效性和鲁棒性,本节选取了6个具有复杂性背景的图像序列1数据集下载网址:http://cvlab.hanyang.ac.kr/tracker_benchmark/datasets.html.,包括Car4,CarDark,Deer,Freeman1,Subway,Walking2.此外,TSSR算法与其他先进的目标跟踪算法进行比较,包括L1跟踪器[16]2L1跟踪器代码下载网址:https://www3.cs.stonybrook.edu/~hling/code_data.htm.、SCM跟踪器[26]3SCM代码下载网址:https://github.com/huchuanlu/12-1.、MTT跟踪器[2]4MTT代码下载网址:https://sites.google.com/site/zhangtianzhu2012/publications.以及基于深度特征的目标跟踪算法Siam-Mask[27]5SiamMask代码下载网址:https://github.com/foolwood/SiamMask..本节实验在Window 10 平台上MATLAB R2017b软件中完成,跟踪结果如图6所示.
在TSSR算法中,设置粒子数为600个,高斯核函数中的常量参数为σn=0.7和=5.算法1中的λ=0.11,γ=0.11,η=0.05,模板更新阈值τ=0.76.在目标与背景具有相似纹理和颜色的情况下,可以适当降低模板的更新阈值,来保证模板中不会出现非目标信息,并且目标模板的初始化与L1跟踪器[11]相同,目标模板数为10个.
5.1 定量分析
本小节通过计算中心定位误差以及重叠率,对上述5个算法在6个数据集上的跟踪实时性以及跟踪效果进行定量分析.其结果分别如图4和图5所示,表4-6分别列出了每种算法在各个数据集上的帧速率、平均中心误差和平均重叠率,跟踪实时性以及跟踪效果最好结果在表4-6中用加粗字体进行标注.
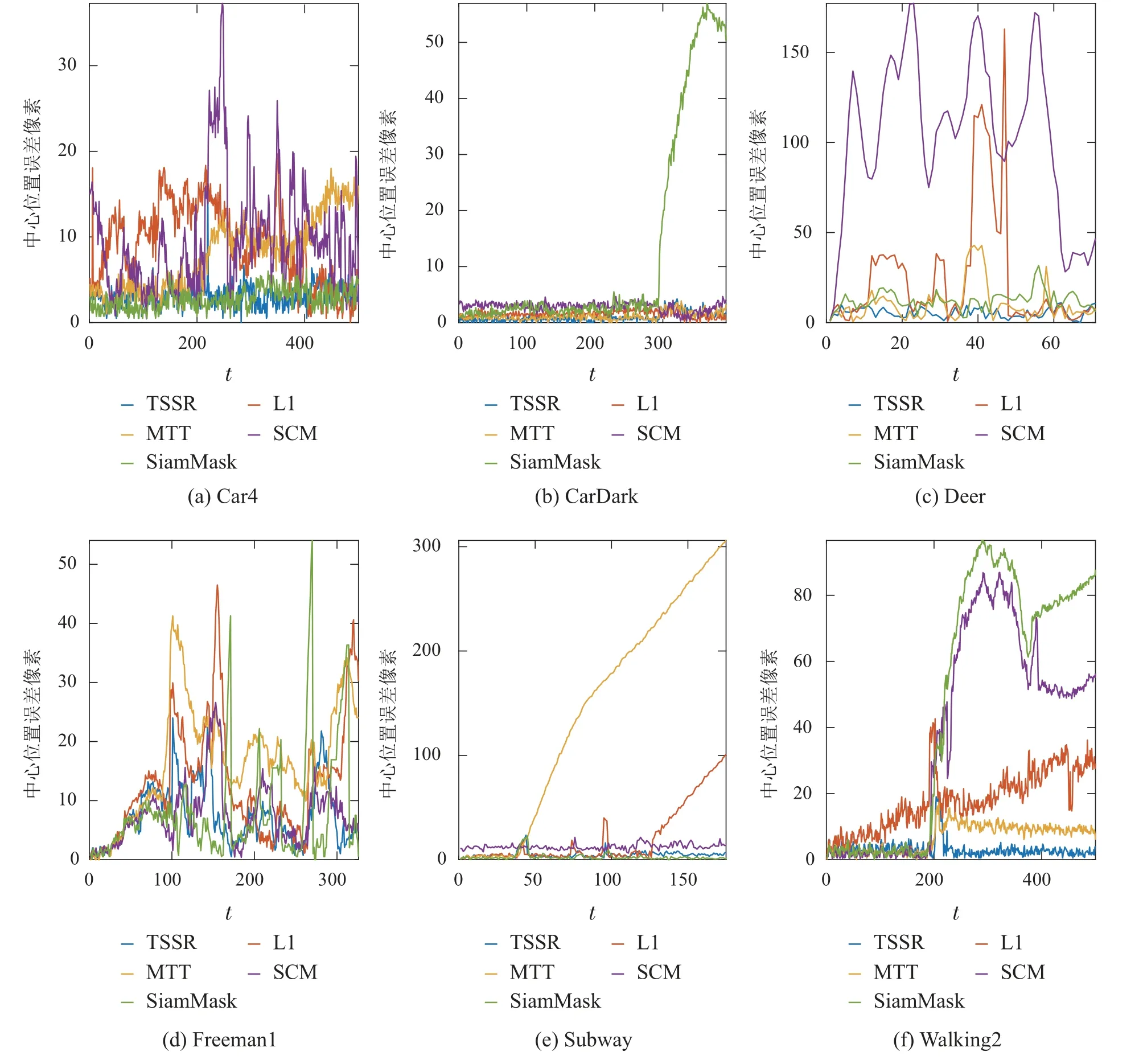
图4 中心误差Fig.4 Center error
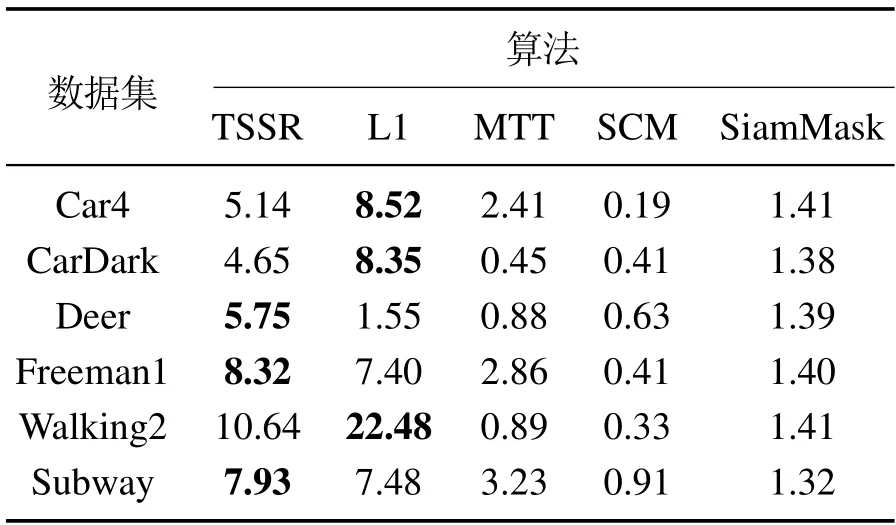
表4 帧速率Table 4 Frames persecond
这些数据集包含了实际情况中的诸多复杂因素,比如视角变化和部分遮挡.视角变化即由于目标与相机之间的相对运动,从而导致目标在不同帧图片之间的外观存在较大的差异.如图6中Car4数据集所示,目标车辆从视野的左侧移动到了右侧,且外观变小;Deer 中的目标发生了旋转;Freeman1中目标人脸的外观在六帧图片之间都存在着较大的差异;Walking2中的目标在视野中由近及远,外观大小也出现了较大变化;Subway中的目标在视野中在从左往右前进的过程中也出现了外观变化.从表5和表6可以看出,本文的算法在存在是视角变化的数据集上平均中心误差分别为2.46,5.41,7.38,3.04,2.53,平均重叠率分别为0.85,0.72,0.45,0.77,0.56.说明本文算法可以很好应对视角变化带来的挑战.
在注重植物选择多样性的同时,还要注重植物种植的层次性,在植物景观中植物的层次结构是非常重要的。大多数的景观忽略了这一点,导致植物景观整体看起来不够灵活或者给人一种混乱感。景观营造较好的模式应是乔木、灌木、草本相结合的立体结构模式。
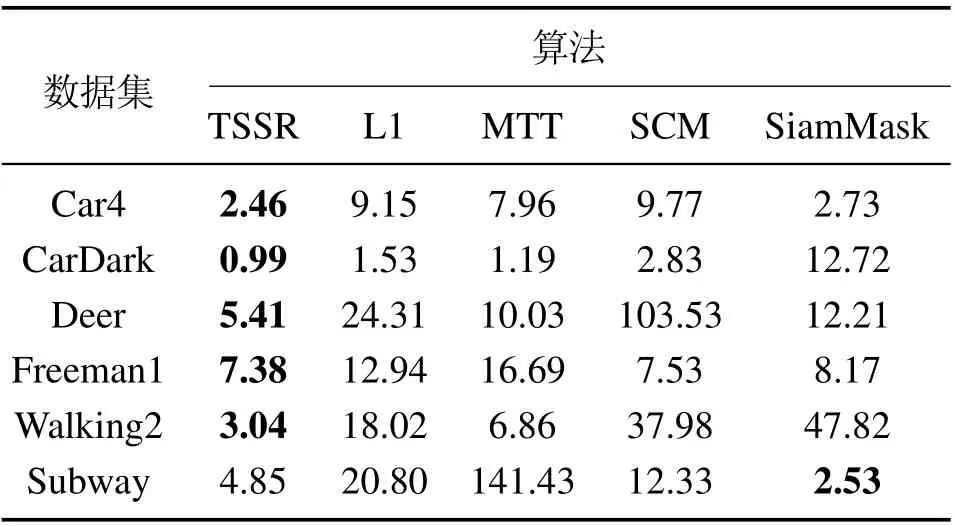
表5 平均中心误差Table 5 Average center error
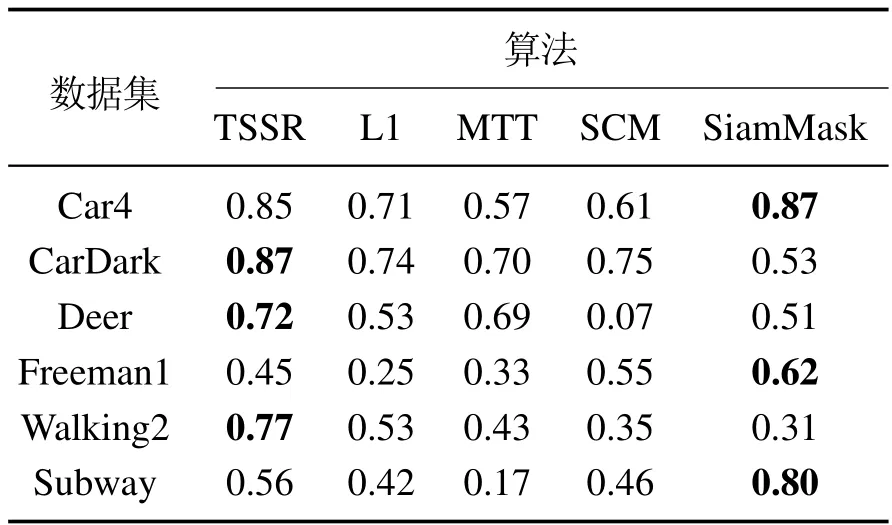
表6 平均重叠率Table 6 Average overlap rate
遮挡即目标的整体或部分被非目标物体遮挡.如图6所示,Freeman1数据集中目标人脸在第302帧被人手遮挡;Walking2的目标在第196,202和218帧图片中被一名男子遮挡;而Subway数据中目标也存在被不同人遮挡的情况.从表5和表6可以看出,本文的算法在存在遮挡的数据集上平均中心误差分别为7.38,3.04,4.85,平均重叠率分别为0.45,0.77,0.56.虽然在这3个数据集上,TSSR的结果稍差于基于深度学习的Siam-Mask算法,但从图6可以看出,SiamMask在Walking2上出现了跟踪失败的情况,因此,本文的算法拥有较好的鲁棒性.
本文利用图像的信息熵来表示图像的复杂度,计算每个数据集中图像的平均熵来度量数据集中的背景复杂度.Car4,CarDark,Deer,Freeman1,Subway以及Walking2数据集的平均熵分别为6.92,6.70,7.29,7.38,7.25,7.46,其中,Walking2数据集的平均熵最高,复杂度也最高,而本文的算法在Walking2数据集上的跟踪效果也优于其他4个算法.
从表4可以看出,本文所提的TSSR算法以及L1跟踪算法在6个数据集上都具有较高的帧速率,但TSSR的帧速率较L1更稳定,所以本文所提算法拥有更好的实时性表现.从表5和表6可以看出,本文所提的目标算法具有较高的帧速率、较低跟踪误差以及较高的重叠率,跟踪效果优于其他4个算法.
5.2 定性分析
为了验证TSSR算法的鲁棒性,利用上述6个数据集,测试了每个算法在出现光照变化、目标尺度变化、遮挡、形变、运动模糊、快速移动、面内旋转、面外旋转、背景杂波等挑战下的跟踪效果,结果如图6所示.
Car4数据集是在一个开放道路上获取的,主要存在2种复杂性挑战:光照变化,目标尺度变化.在图6的第1行显示了4个算法在第91,175,194,223,290,399帧图像的跟踪效果,其中在第175,194,223帧时出现剧烈的光照变化,MTT和SCM的跟踪效果变差,而TSSR,L1以及SiamMask算法跟踪效果没有明显变化,可以较好地抵抗光照变化带来的干扰.

图6 目标跟踪结果Fig.6 Objective tracking results
在CarDark数据集上主要存在2种挑战:光照变化,背景杂波.SiamMask算法在第302帧图像后便不能正确地跟踪目标,而其余4个算法都可以较好地跟踪目标,没有出现目标跟踪失败的情况.此外,从图4和图5可以看出,TSSR算法跟踪效果优于其他算法.

图5 重叠率Fig.5 Overlap rate
Deer数据集上主要存在4种复杂性挑战:运动模糊,快速运动,面内旋转,背景杂波,跟踪难度也比上述Car4和CarDark两个数据集高.从第16,38,42,56帧图像可以看出,SCM和L1算法会出现目标跟踪失败的情况,但TSSR,MTT和SiamMask算法可以始终跟踪上目标,在第38,42帧图像中MTT算法受到背景杂波的干扰,会出现目标跟踪失败的情况,在第56帧时,由于背景杂波的影响,SiamMask算法同样出现跟踪失败的情况.
Walking2数据集主要存在3种复杂性挑战:遮挡,目标尺度变化,背景杂波.相比于Car4和Freeman1数据集,Walking2数据集中目标的比例变化更大,跟踪难度也相应的变大.通过第202帧图像可以看出目标的被遮挡面积超过了目标本身面积的80%,并从第218,235和376帧图像中看出SCM和SiamMask算法出现了目标跟踪失败的情况,L1算法并不能很好的应对目标比例变化的挑战,MTT算法虽然能跟踪上目标,但无法准确选择目标区域,只有TSSR算法表现出了较好的跟踪效果.
在Subway数据上存在2种复杂性挑战:遮挡,形变.并且存在目标被多次遮挡的情况,相比与Walking2,Subway数据集上的遮挡挑战难度更大.从第45帧开始之后的所有帧图像中,MTT算法都未能跟踪到目标.对于其他算法,SiamMask算法在第45帧图像中出现了跟踪失败的情况;L1算法在第166帧图像中出现了跟踪失败的情况,只有TSSR和SCM算法始终可以跟踪上目标,从第51,103,166帧图像可以明显看出,TSSR算法要优于SCM算法.
6 总结
本文针对目标跟踪问题,基于粒子滤波框架,提出了TSSR目标跟踪模型,将跟踪问题转化为在原始空间和特征空间中的两阶段稀疏逼近问题,同时针对在特征空间中的稀疏表示模型,提出了一种基于核方法的加速近端梯度算法.针对目标跟踪中出现的多种干扰,本文通过在特征空间中利用核函数计算当前时刻跟踪目标与模板的相似度量来决定是否更新模板.最后通过对比实验验证了本文所提出的TSSR方法在针对视角变化和部分遮挡因素的鲁棒性.
