新型多旋翼作业型空中机器人自抗扰控制
2022-05-21许昌亮姜遇红周东升廖禄伟张秋雁
许昌亮 ,杨 忠 ,姜遇红 ,徐 浩 ,周东升 ,廖禄伟,张秋雁
(1.南京航空航天大学自动化学院,江苏南京 211106;2.南京航空航天大学无人机研究院,江苏南京 210016;3.贵州电网有限责任公司电力科学研究院,贵州贵阳 550002)
1 引言
高压输电线路通道附近的树木时常会超过安全距离从而引起线路通过树木对地放电,造成停电、火灾等安全事故,给社会生产生活带来了巨大的不便.因此每年电力部门耗费了大量资源用于树障清理工作,目前其主要方式大多使用人力,辅以手锯等简单工具来操作.该种清理方式不仅效率有限,且人的安全无法保证,在我国该类任务所引发的伤亡事故时有发生.故研发并推广一套能够代替人工清理方式的高效、安全的树障清理空中机器人尤为必要.
要设计一款能够进行高效空中作业的机器人,首先想到的是以类似大疆无人机的传统结构多旋翼为飞行平台主体,并装配合适的作业装置.该类能够垂直起降和空中悬停的多旋翼空中机器人具有结构简单和稳定性好等优点,以其为作业平台的应用研究得到广泛关注[1-4].常见多旋翼飞行器的旋翼一般采用平面配置,即旋翼固定在同一平面[5],这使得飞行器需要通过大角度的姿态配合来完成移动,这也是目前制约传统结构旋翼飞行器实现接触作业应用的重要因素.因为在空中机器人进行空中作业的过程中,既需要进行前后平动,又要保持机体姿态稳定来维持作业工具的姿态稳定,这在传统平面配置旋翼构型空中机器人上是无法实现的.在树障清理作业任务中,大幅度的姿态变化将极易导致作业工具卡阻在树障上.所以此控制问题的本质包括两个方面:1)使机器人保持姿态平衡,尤其是保持零俯仰角;2)使机器人较好地抵御作业过程中的外力扰动,维持姿态稳定.
因此本文有必要采用全新构型来克服传统构型中物理缺陷,大致存在两种提高多旋翼空中机器人平动性的方法:一是采用倾转旋翼飞行器[6-8].倾转旋翼飞行器可以通过位置和姿态的解耦控制,满足环境对作业平台的平动性要求.倾转旋翼飞行器虽具有更高的能源利用率,但也存在机械结构复杂的缺点;二是采用非平面旋翼配置,将旋翼翼面定为固定的倾斜方向,通过调节不同方向上旋翼推力的大小,该类全驱动飞行器[5,9-10]可以达到调节总推力和扭矩的方向与大小的目的,提升空中机器人的平动性能.然而,这类飞行器由于各旋翼之间存在较大的内相互作用力,具有较低的能源使用效率,并且前人研究的关注点更多在于提升飞行器的平动性能或某些指标.
作业任务除了对平台的平动性有较高要求之外,机器人平台装载的作业工具引起俯仰和偏航通道的大惯量以及作业时的接触力影响也要求平台具有较强的抗扰能力,除了将平台推力矢量化之外,采用具有抗扰动效率更高的飞行控制策略也受到关注,滑模控制、误差符号函数积分的鲁棒控制算法(robust integral of signum of error,RISE)和自抗扰等控制方法或技术能够较好地抑制来自作业环境或平台内部的干扰[11-15],选择一个合适控制方法首先要明确被控对象和作业任务的特点.本文的课题背景是研发一款作业型空中机器人,可实际工程应用于高压输电线路通道的树障清理.故对于控制算法的要求包括:1)具有较好的抗扰性能来维持机器人在作业过程中接触复杂外力作用时的姿态稳定;2)易于工程实现,这要求算法计算量较小,并可在机载微控制器(microcontroller unit,MCU)上实时运行.
自抗扰控制(active disturbance rejection control,ADRC)技术可以不要求被控对象准确建模,且能够有效抑制系统内外扰动,因为它可以实时估计系统的内部扰动和外部环境未知扰动作用并予以补偿[16-18].而树障清理机器人在作业过程中,接触作业带来的外部作用力对机体是巨大扰动,给姿态稳定控制带来很大挑战.另外,ADRC具有运算量较小的特点,使它易于在MCU上实现实时控制机器人的位姿[19].而且其控制器参数的适应对象范围也较大[20].另外,尚无自抗扰控制方法用于非平面旋翼空中机器人的报道.
基于以上分析,在机器人结构上,本文设计了一种能够用于树障清理作业的空中平台,要求平台能够在悬停的基础上,无需姿态俯仰变化即可实现前进与后退的平移运动.在控制方法上,根据树障清理任务需要,由于非平面多旋翼空中机器人在飞行过程中往往具有较大的内作用力、转动惯量并受到树障接触力干扰,因此为其设计能够估计并抑制扰动的自抗扰飞行控制律.本文的自抗扰形式采用非线性ADRC,非线性ADRC相比线性ADRC的优势在于跟踪精度更高和抗扰能力更强[21].另需说明的是本文采用非线性自抗扰方法有两个考虑:一是自抗扰控制方法的提出者韩京清教授倡导使用非线性自抗扰控制;二是接触式作业树障清理是新的应用场景,其特点是作业环境复杂、扰动强度大,采用非线性自抗扰控制会更为可靠.
本文剩余内容安排:首先详细描述所设计的作业型多旋翼空中机器人构型,并建立机器人数学模型;接着设计空中机器人的位置和姿态跟踪控制律;然后在MATLAB/Simulink中设计数值仿真实验以验证所设计飞行器及其控制律的有效性,同时也通过设计的物理样机验证了本文提出的控制律的良好控制效果;最后一节总结全文.
2 作业型空中机器人结构设计
本节主要介绍空中机器人的新型结构设计.空中机器人进行树障清理作业时需要携带作业机械臂,该机械臂位于机腹正中间,机体轴所在位置.在空中机器人机腹增加一套涵道推进器.
作业平台的外形、各推进器的推力及旋翼旋转的方向、机体坐标系Obxbybzb、世界坐标系Owxwywzw、机械臂和配重(电池)的示意如图1所示,其中Ob位于机体质心.

图1 作业型空中机器人模型示意图Fig.1 The model diagram of the aerial robot with manipulator
由以上图文描述,可以将本文设计的作业多旋翼空中机器人模型抽象为3个部分:1)机腹下方悬挂的两个推进器,对称分布在xb的两侧,能够产生沿轴xb的正反推力,输入量为期望电机转速,输出量为推力和扭矩;2)X模式四旋翼空中机器人载具机身,可以简单抽象为普通X模式四旋翼无人机;3)作业机械臂,由于作业过程中,加装刀锯的机械臂要远离作业对象以保证机身安全,因此这部分带来的影响包括,一是与作业对象接触后,带来反作用力或者称为扰动,二是对四旋翼空中机器人模型参数的影响,导致模型参数中绕机体坐标系yb和zb的转动惯量较普通四旋翼明显增大,增加空中机器人的控制难度.
本文所用部分符号代表的含义如表1所示.

表1 本文常用符号含义Table 1 Explanations of parameters used in this paper
3 作业型空中机器人数学模型
上一节本文完成了机器人的结构设计,在控制律设计之前,有必要对机器人进行动力学建模.
3.1 X模式四旋翼产生的力和力矩
四个旋翼产生的推力与zb平行,指向zb负方向,与转速有如下关系式,其中krf为旋翼升力系数:

因此,四旋翼产生的合力fr有如下表达式:

考虑反扭矩之后,四旋翼系统产生的三轴合力矩与转速存在以下关系,其中lr为各旋翼与质心的距离在xb或yb轴的投影长度(或称为力臂),krm为各旋翼的反扭矩系数.
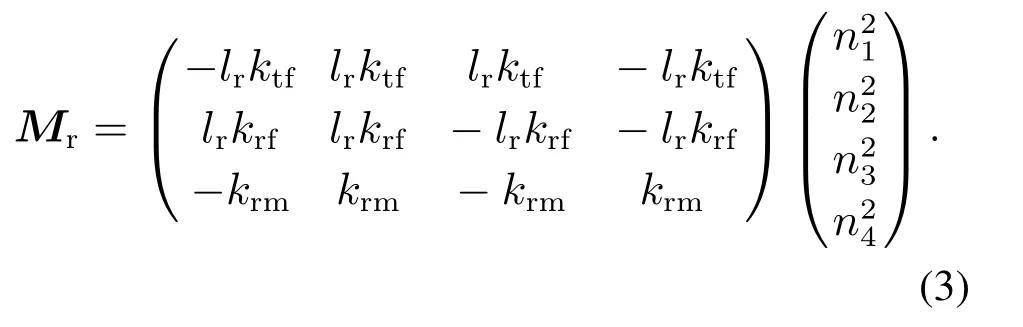
3.2 推进器的力和力矩
推进器产生的推力为f5和f6,它们与推进器电机转速存在关系如下,其中ktf为推进器的推力系数:
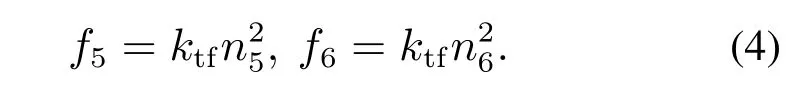
推进器产生的三轴力矩Mt主要由推力不过质心引起的扭矩以及电机反扭矩组成,有如下表达式,其中:lty和ltz分别为两个对称分布的推进器质心与机体质心的距离在yb和zb轴上的投影长度,ktm为推进器的反扭矩系数:
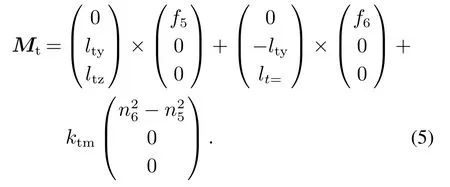
3.3 空中机器人作业负载受力分析
清障空中机器人搭载双刀锯,其进行作业过程中的受力情况如图2所示.
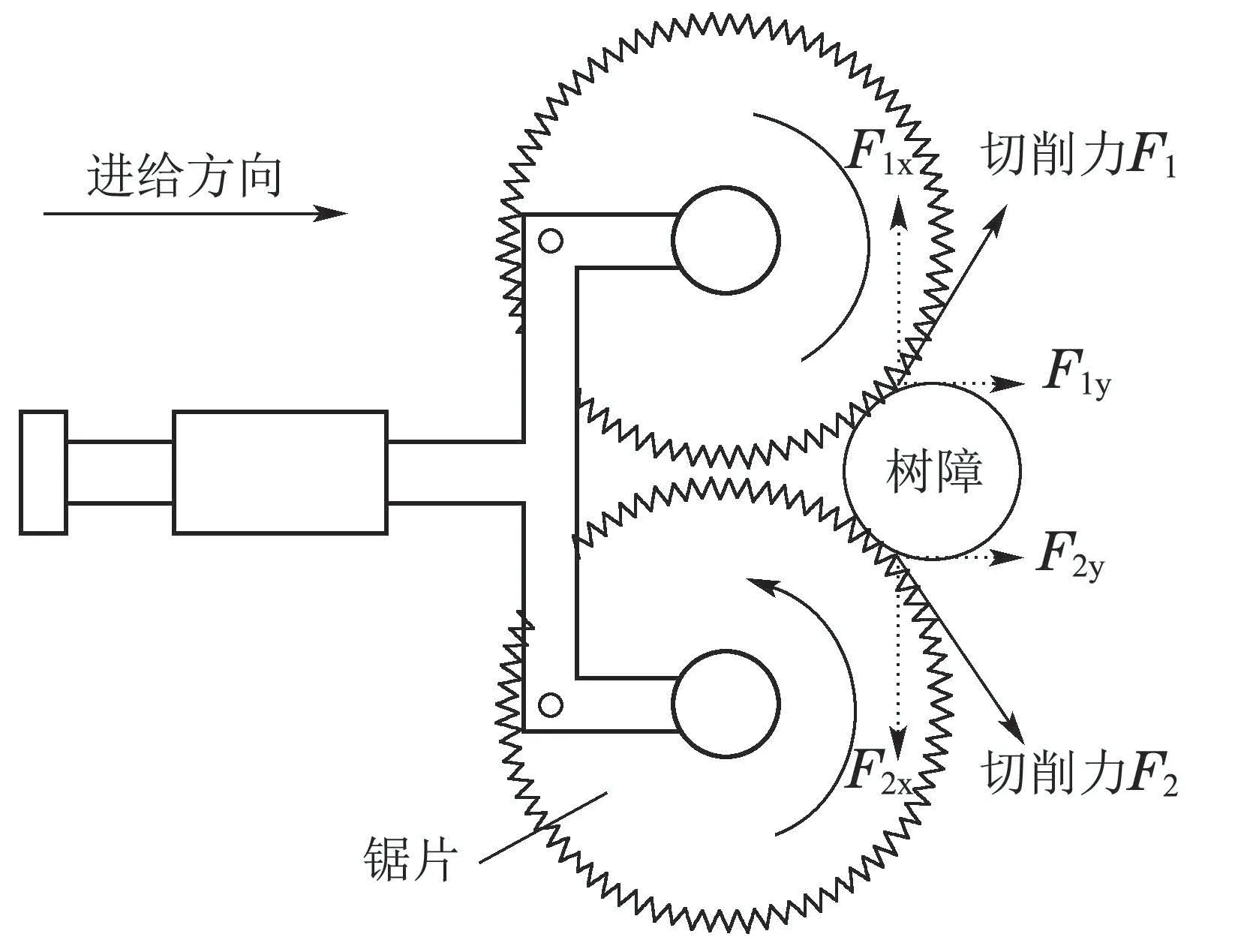
图2 空中机器人作业负载受力分析Fig.2 The force analysis of load during operation
对切削力F1,F2进行分解,其中Fx表示主切削力,Fy表示树枝对接触式作业空中机器人的反作用力.Fx=F1x+F2x,Fy=F1y+F2y.由于Fy过机器人的质心,故不对空中机器人姿态通道造成影响,因此只考虑由主切削力Fx引起的扰动.
主切削力对机器人产生的干扰力矩bmτc如下:

其中:b3=[0 0 1]T,ls为刀锯前端至树障清理空中机器人质心的距离.则有

其中Fx可以根据如下公式计算:
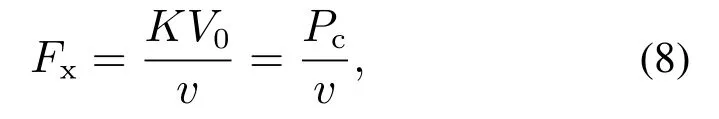
式中:V0表示锯片每单位时间切割的树枝体积,Pc为切割功率,K和v分别为锯片的切割力和线速度.同时

其中P0,Pe分别代表直流电机的空载功率和电磁功率.在实验过程中,利用机载传感器可以直接测量直流电机的电流、电压、转速等参数.然后,结合上述公式,可以计算出扰动力矩的近似值.
3.4 空中机器人的位姿运动模型
综上所述,根据牛顿欧拉运动定律,得到机体位置和姿态的动力学模型如下:
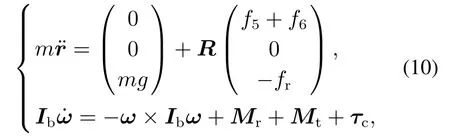
其中:m为机体质量,g重力加速度,Ib为三阶对角矩阵diag{Ix,Iy,Iz}为3阶对角阵,对角元素分别代表平台绕3个机体轴的转动惯量,R为OExEyEzE与Obxbybzb的变换矩阵,表达式如下,其中,为了简化书写,C代表cos,S代表sin.
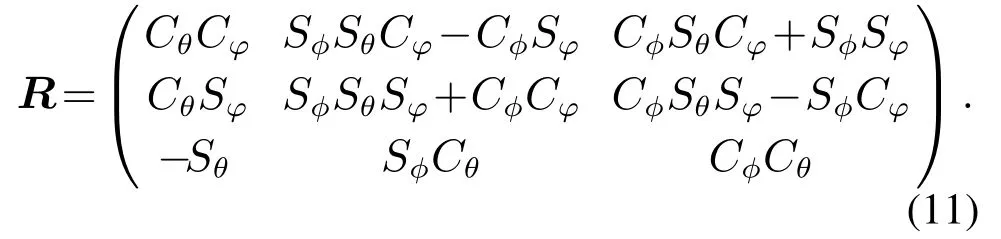
此外,机体的角速率与姿态角变化率存在如下关系:
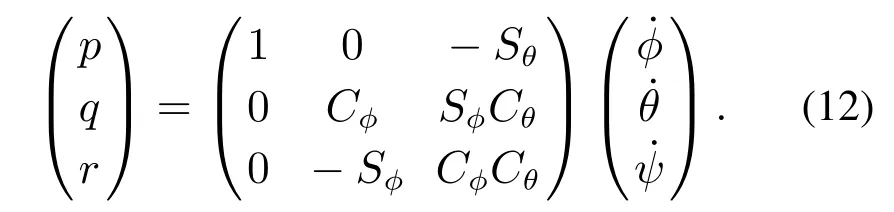
上述各项机体物理参数如表2所示.

表2 空中机器人物理参数Table 2 The physical parameters of the aerial robot
4 自抗扰飞行控制律设计
基于本文引言的分析,本节阐述了采用非线性自抗扰控制方法来实现清障机器人的位姿控制的过程.首先给出控制律的总体框架设计,然后分别从位置和姿态两环来具体实现.之后给出了稳定性证明.
4.1 控制律设计总体描述
控制律采用内外环策略,外环为位置闭环跟踪控制,内环为姿态闭环跟踪控制.
根据位置和姿态的实际值(x,y,z,φ,θ,ψ)和期望值(xd,yd,zd,φd,θd,ψd)产生四旋翼电机和水平推进器电机的期望转速的步骤如下:
步骤1位置跟踪控制律根据(x,y,z)与(xd,yd,zd)计算控制量,代表沿世界坐标系三轴的虚拟作用力.
步骤2允许的俯仰角变化幅度默认为0,当空中机器人处于非作业状态时,可以修改为非0.因此,期望的俯仰角θd为0,期望偏航角ψd由人为设定,一般设置为0.基于此,可以根据动力学方程将变换为(U5,U1,φd),U5为期望两个水平推进器产生的合力,U1为期望四旋翼系统产生的合力.
步骤3姿态跟踪控制律根据实际姿态(φ,θ,ψ)和期望姿态(φd,θd,ψd)产生控制量(U2,U3,U4),分别代表绕机体坐标系下3个坐标轴的虚拟控制扭矩.
步骤4为了使水平推力对平台姿态产生的影响尽可能小,这里令n5和n6相等,并且水平推力引起的力矩MMMt在姿态控制律中被当成扰动由扩张状态观测器(extend state observer,ESO)估计,并在控制律中给予补偿.
步骤5将(U1,U2,U3,U4)根据下式转换为


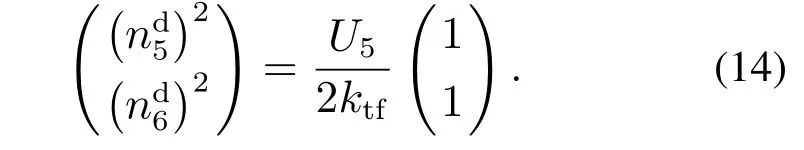
综上所述,控制律的结构如图3所示.
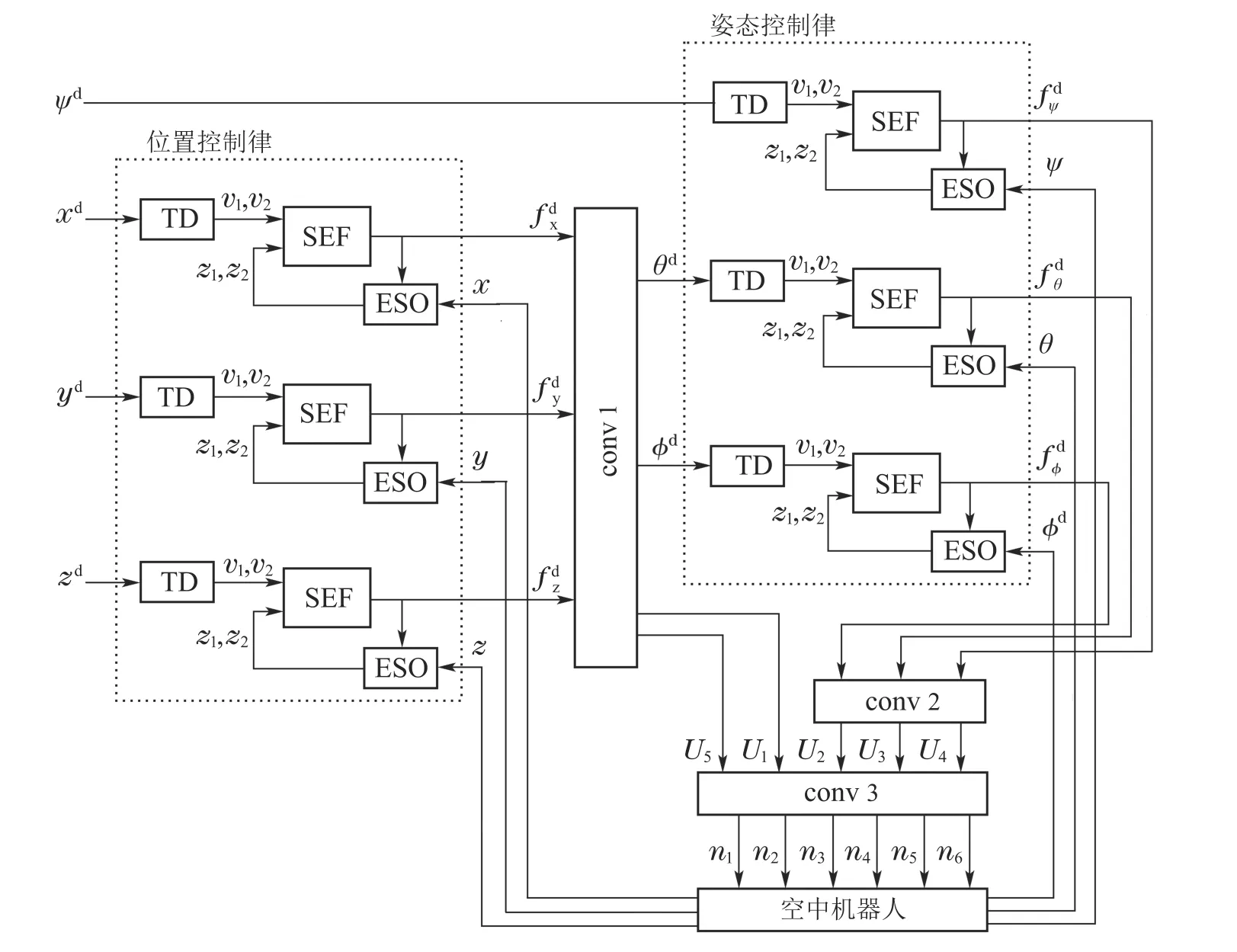
图3 位姿跟踪控制律结构框图Fig.3 The diagram of the control law for the attitude and position tracking
4.2 位置自抗扰控制律
空中机器人位置运动模型的描述形式为多输入多输出(multi-input multi-output,MIMO)系统,为了能够将适用于单输入单输出(single-input single-output,SISO)系统的ADRC应用于设计空中机器人的位置跟踪控制律,这里首先将系统方程的描述形式通过引入虚拟控制量的方式变换为由多个SISO方程组合表达


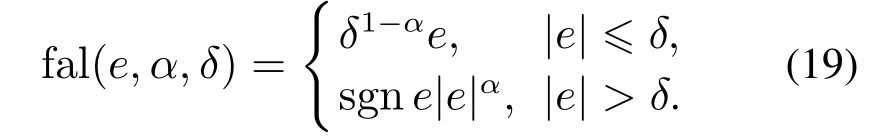
观测器的稳定性和收敛性已经得到证明[22-23],本文将在第4.4节给出闭环稳定性证明.
之后,为参考输入信号采用跟踪微分器(tracking differentiator,TD)设计过渡过程,二阶TD表达式如下:

式中:v1跟踪参考输入xd,(v2,fh)分别是过渡过程v1的一二阶导数,fhan由式(19)表述,该式中(r,h)为可调参数.
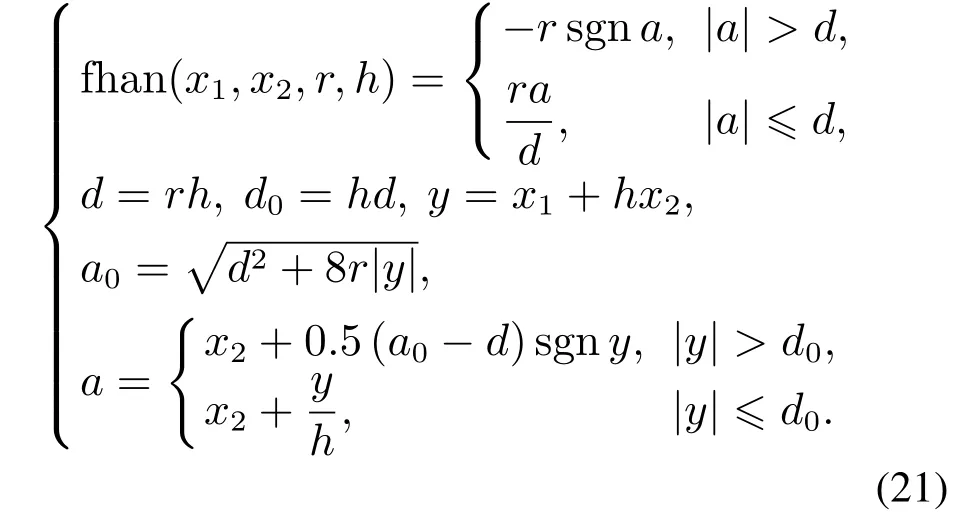
最后,采用如下状态误差反馈律(state error feedback,SEF),其中(r,h)与式(21)参数意义一致,c为阻尼因子也需要调节.
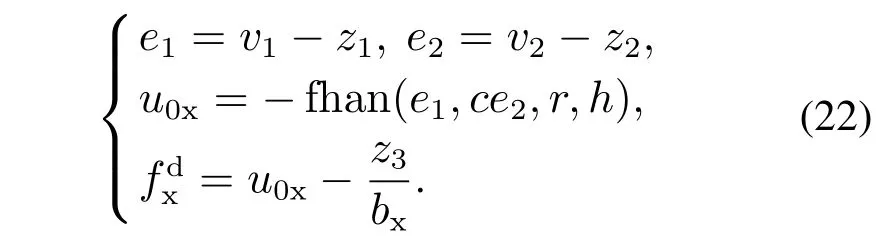
因此该通道控制律的结构如图4所示.
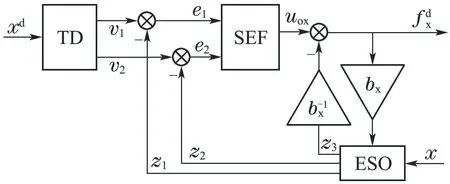
图4 空位置x自抗扰跟踪控制律Fig.4 The control law of position x tracking using ADRC
位置y和z的控制律与x的类似,这里不再详细说明.
4.3 姿态自抗扰控制律
空中机器人角运动方程由(p,q,r)描述,而这里需要实现的是姿态角(φ,θ,ψ)运动控制律,因此需要根据式(12)将角运动方程的状态变量由(p,q,r)转换为(φ,θ,ψ).同时,由于机器人作业过程中不会出现大的姿态波动这里采用小角度假设[12,14],此外,本文采用了ESO估计包括建模不精确部分的内外总扰动,因此这里可以应用空中机器人姿态角小角度变化的假设,从而式(12)可近似为下式:
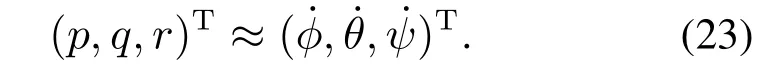
于是角运动方程可改写如下:
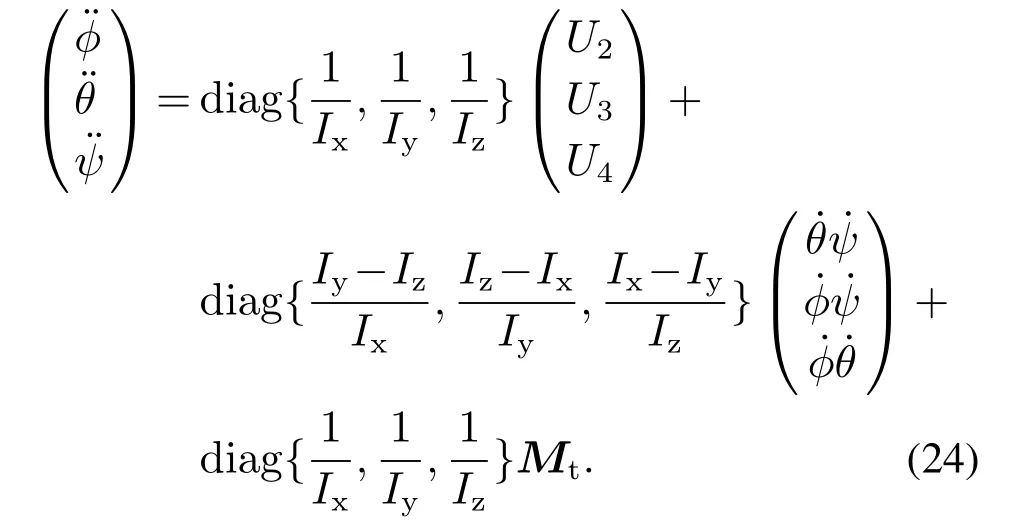
将耦合项、MMMt和可能存在的外部扰动合并作为系统扰动(dφ,dθ,dψ),进一步改写方程式如下:
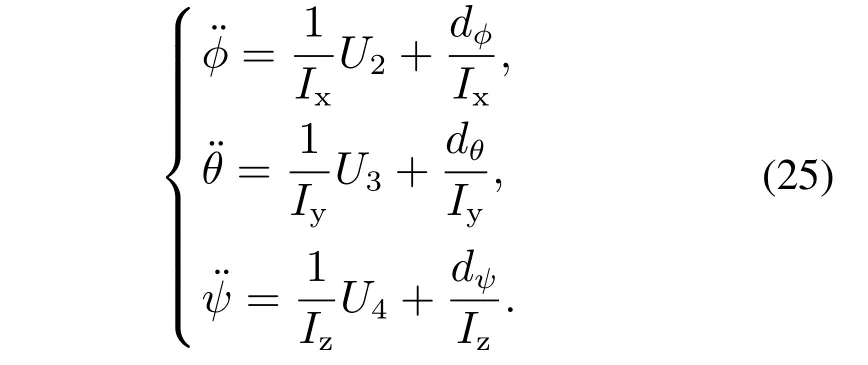
从以上方程式可以看出,该运动方程为SISO形式.因此ADRC适用于设计该子系统的运动控制律.
下面以φ通道为例,说明姿态自抗扰控制律的设计过程.将式(25)中φ相关方程重写如下:
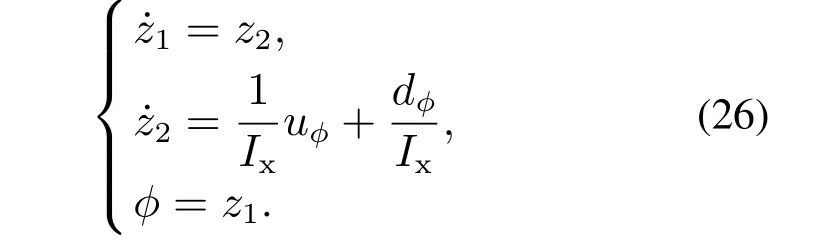
设计离散ESO,其表达式与式(18)类似,只是其中的x(k)变为φ(k).同样地,采用TD为参考输入设计过渡过程,其表达式与式(20)类似,其中x(k)变为φ(k),但是过渡过程的时间应尽可能短,因为过程中需要姿态角φ作为位置的执行器,其具有较快的响应速度可以提高系统稳定性.最后,采用与式(22)类似的SEF.
姿态θ和ψ的ADRC控制律与φ的类似,这里不再具体说明.
4.4 闭环收敛性分析
这里将以位置x通道为例分别证明观测器的收敛性和闭环收敛性.
将含有扰动的动力学方程重写为,其中dx为可能存在的内外总扰动,ux代表.
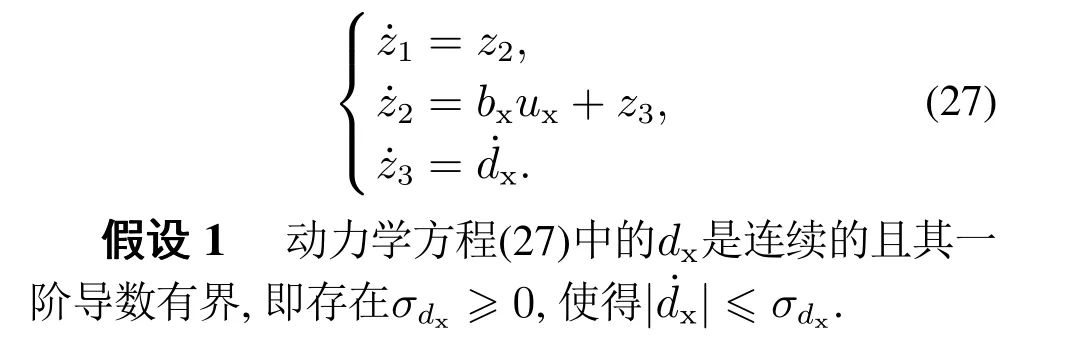

引理2在假设1成立的条件下,观测器误差有界,则存在参数k1>0,k2>0,使系统(33)的跟踪误差有界,即存在σ2>0,使得‖eee‖≤σ2[24].
引理3对于任意有界可测函数xd,存在σ3>0,使得|v1-xd|<σ3[25-26].
推论1在dx连续且一阶导数有界,xd函数可测的条件下,由引理2 和引理3可以推出,存在σ >0,使得|z1-xd|<σ.
5 实验验证研究
为了验证所设计的空中机器人合理性及其控制律的有效性,即前后平移运动无需姿态配合和空中机器人的抗干扰性能,本节安排了仿真实验和物理样机实地作业实验来验证自抗扰控制算法的控制效果.
5.1 仿真实验及结果分析
下面将设计空中机器人一系列仿真实验,分别采用上节所述的ADRC方法和传统控制方法.实验项目包括:机器人位置和姿态系统阶跃响应、轴方向“零俯仰角”平移运动、自抗扰控制律中的ESO估计系统状态和扰动的测试和存在扰动条件下的轨迹跟踪实验.
参数整定是控制器功能实现的重要环节.TD环节有r和h两个可调参数,其中调节过程中可发现如下规律:快速因子r如果变大,则过渡过程一般会缩短,同时h越大,则滤波效果一般会改善,不过会增加相位损失.在ESO环节中,其参数变化常常会造成扰动估计和补偿效果的不同,观测器增益β01,β02,β03可以依靠经验公式来获得理想的整定,另外非线性参数α1,α2,δ可以参考满意值来辅助整定.在SEF环节参数整定中,补偿系数b取决于被控对象的物理模型,在模型未知的情况下进行整定.
仿真过程中,TD参数r都为40000,h为系统采用时间T即0.001;ESO参数
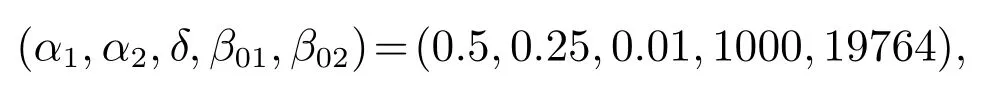
姿态(φ,θ,ψ)和位置(x,y,z)通道ESO的β03分别取值(116280,116280,88207,462920,58278,462920);其余参数如表3所示,此外,虚拟量转换过程用到的参数直接选用相关物理参数.
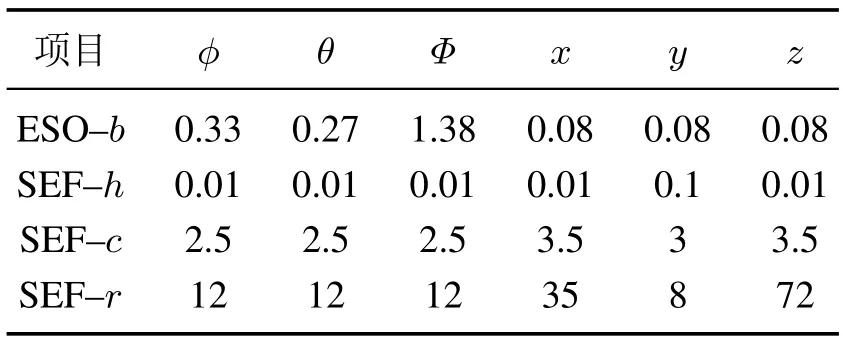
表3 ADRC姿态控制参数Table 3 The parameters of ADRC attitude control
1) 姿态控制律测试.
图5所示为空中机器人的姿态阶跃响应,可以看出姿态3个通道的跟踪控制相比传统方法效果更好.
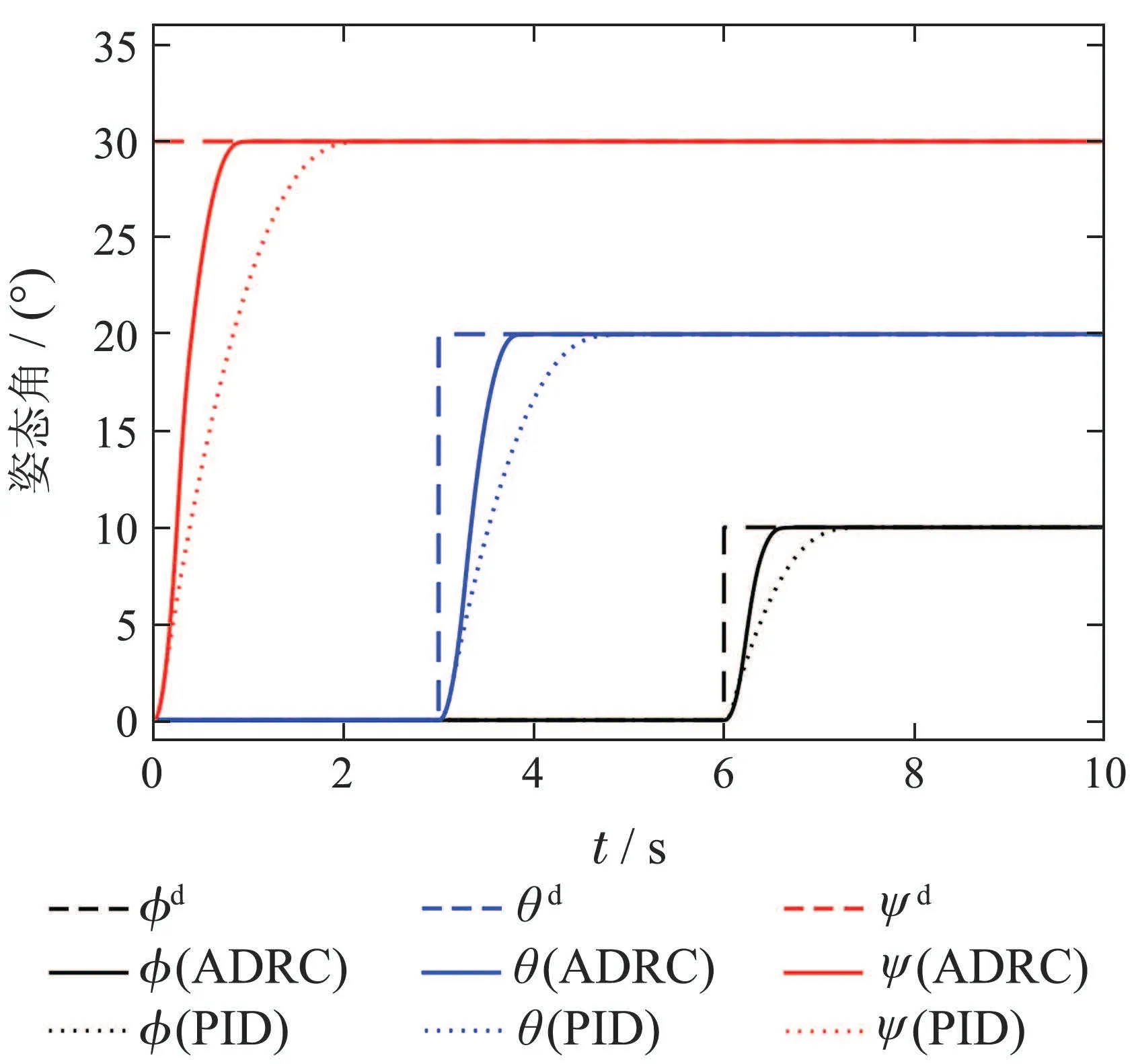
图5 姿态系统阶跃响应Fig.5 The step response of the attitude tracking
2) 位置控制律测试.
图6所示为位置阶跃响应曲线图,3个位置坐标变量分别更好地跟踪了对应的阶跃响应信号,比运用PID方法的效果具有更短的上升时间,从而说明了所设计位置控制律的有效性和优势.同时,为了研究自抗扰控制器在控制能量需求方面的表现,本文给出了本组实验中树障清理空中机器人的控制输入,如图7-8所示.根据旋翼转速与控制能量具有的正相关关系,从图中可以看出,通过与PID控制方法控制输入曲线的对比可以发现,本文所采用的ADRC方法对控制能量的需求比PID控制输入的能量需求稍大,但位置跟踪效果也较好.
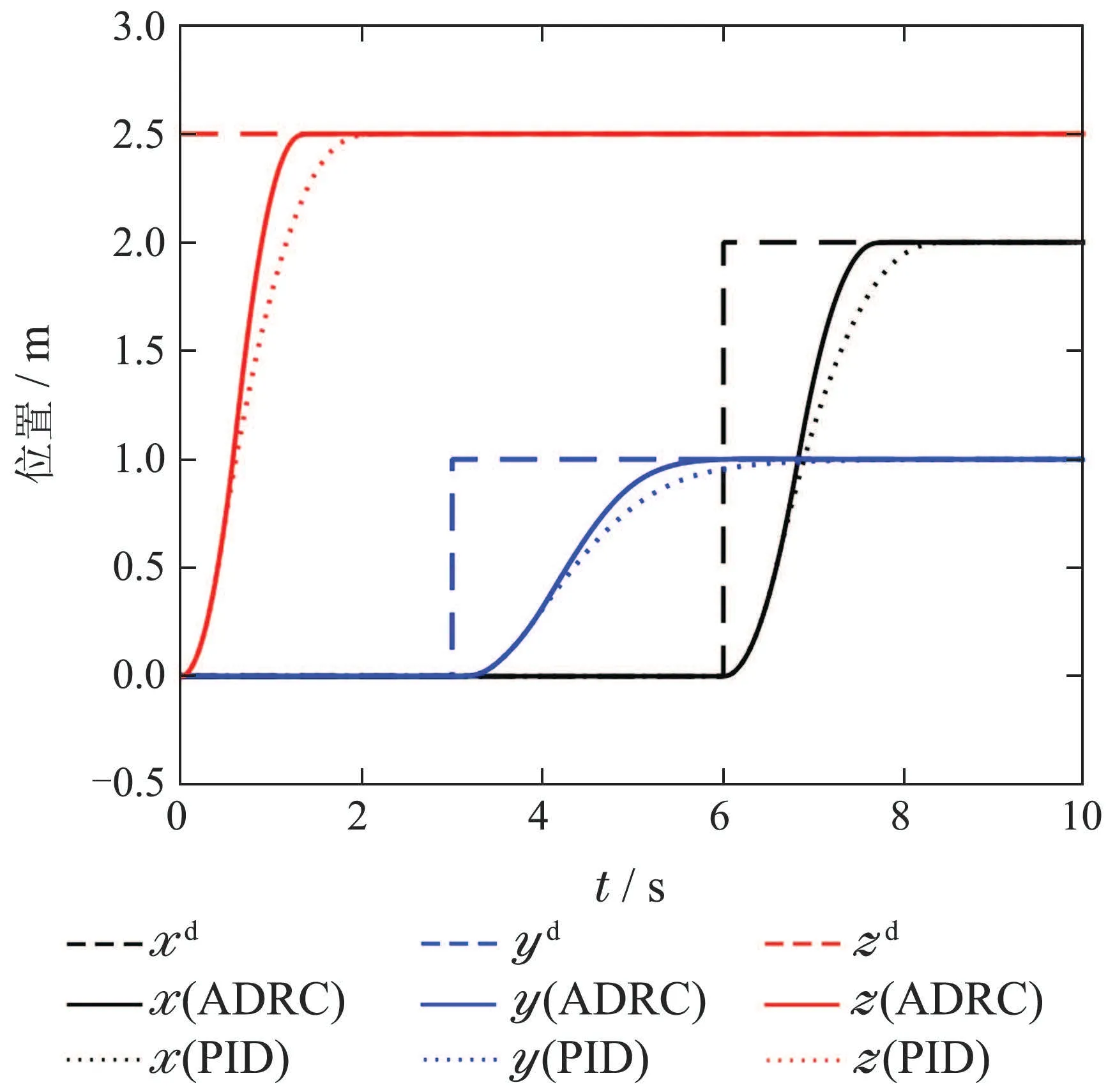
图6 位置系统阶跃响应Fig.6 The step response of the position tracking
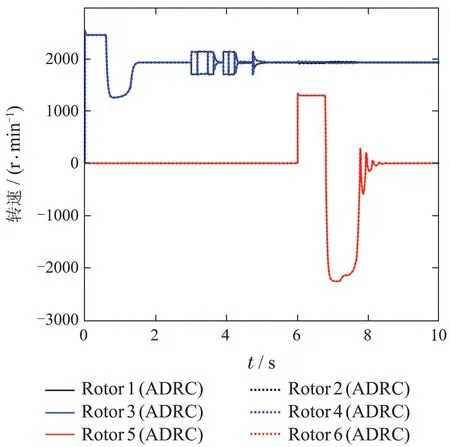
图7 空中机器人旋翼控制输入曲线(ADRC)Fig.7 Control input curve of the aerial robot rotors(ADRC)
3) “零俯仰角”前飞平移运动.
该实验主要验证机器人的平动性能.图9所示为机器人沿位置x前飞运动的情况下,位置和姿态角的变化情况,从上下两幅中可以看出,位置x无需姿态角θ的配合即可完成向前平移运动并准确停车.该实验验证了本文所设计飞行平台的有效性,并满足应用背景需要.其中,位置x变化时,θ发生的微小波动是由于水平推力带来的MMMt需要一定时间才能被ESO检测并补偿.相比之下,使用PID方法所获得的效果明显弱于本文方法,其中前飞平移时俯仰角配合较为明显,“零俯仰”平移效果差强人意.

图8 旋翼控制输入曲线(PID)Fig.8 Control input curve of the aerial robot rotors(PID)
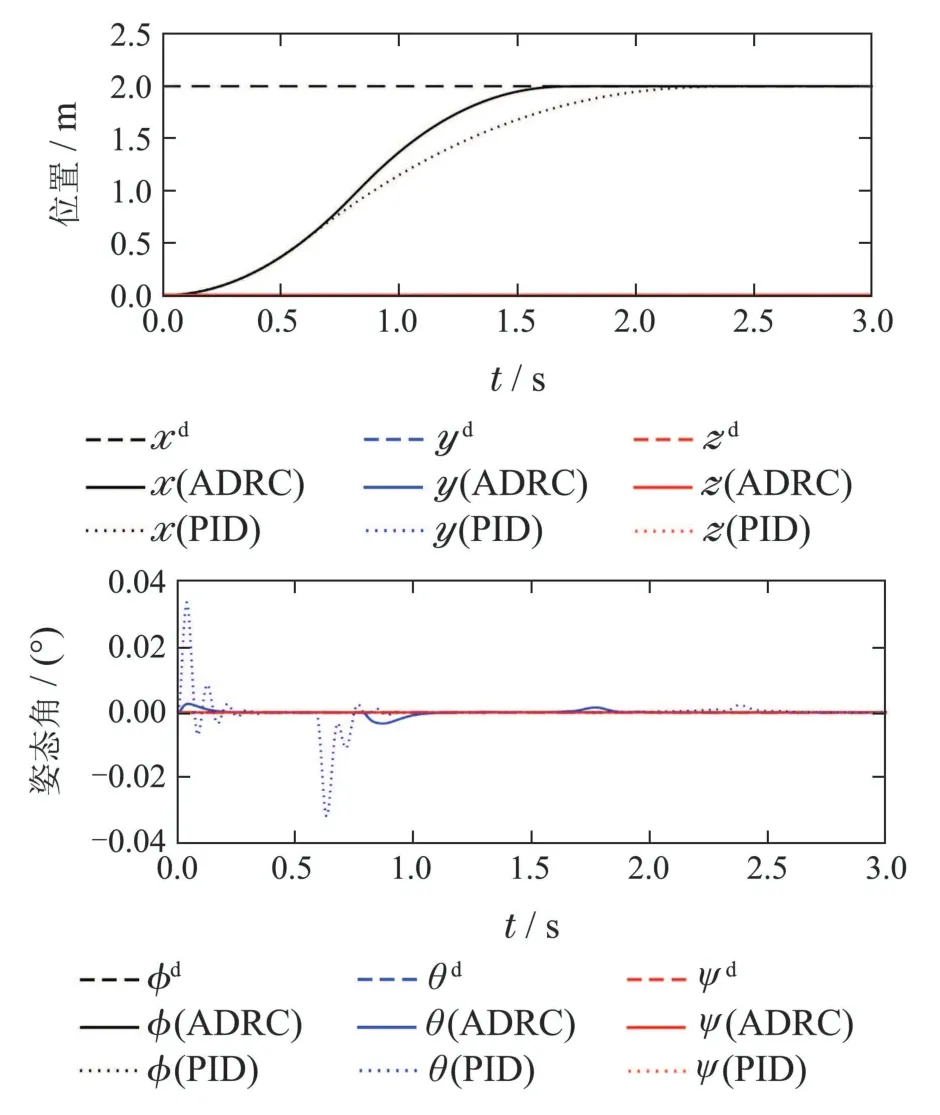
图9 前飞状态下姿态系统阶跃响应Fig.9 The step response of the attitude tracking while flying forward
本实验通过“零俯仰角”前飞平移运动(平动运动)实验验证了水平推力的显著作用.相比于无水平推力部件的传统结构多旋翼,这说明显著发挥了飞行器自身的动力学特性.
4) ESO的扰动估计性能测试.
图10为存在扰动
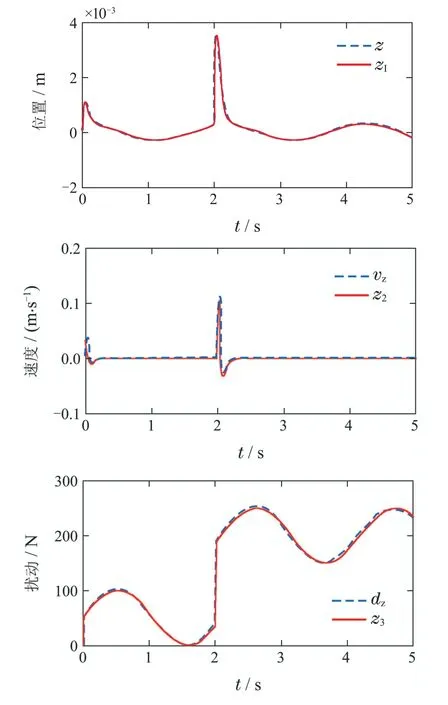
图10 位置z的ESO各状态变化曲线Fig.10 The curves of variables from ESO
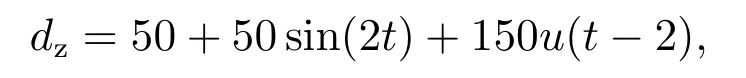
位置z在自抗扰控制律中的ESO分别对位置z、速度vz和扰动的观测值,从图中可以看出,所设计ADRC控制律能够很好地估计并抑制外部扰动力,并且也能够较好地实现对位置及其微分的跟踪.
5) 存在扰动条件的轨迹跟踪.
图11所示为存在扰动
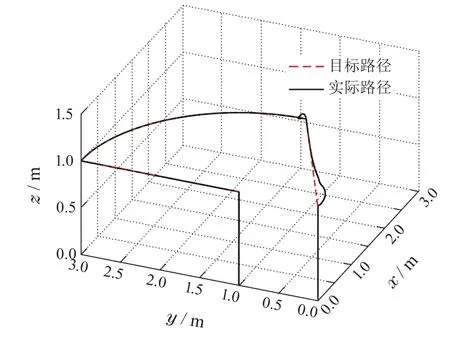
图11 空中机器人路径跟踪曲线Fig.11 The tracking path of the aerial robot
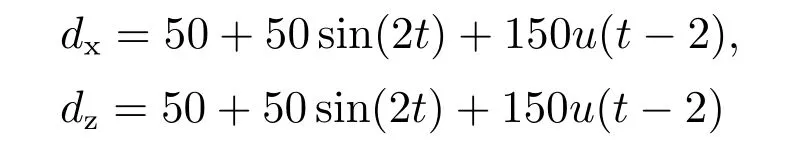
时飞行平台跟踪给定路径的3维飞行轨迹示意图,为了便于观察,这里将位置z数值符号取反,即从负号变为正号.可以看出,即使存在扰动,平台依然能够良好地完成对目标路径的跟踪,说明所设计飞行平台及其控制律具有良好性能.
5.2 物理样机实验及结果分析
为了进一步验证本文的自抗扰控制方法在新型作业型空中机器人上的控制效果,本文开发了一款实验平台样机.该平台样机的飞行控制单元搭载了一款STM32-F427微处理器.本文的自抗扰控制算法以C/C++编程语言的形式植入ArduPilot.为确保获取精确的姿态和位置信息,该平台使用了多传感器融合的方法,其中惯性测量单元(inertial measurement unit,IMU)可获得多达9自由度的运动信息,同时还配备了GPS模块、气压计和超声波传感器.为了获取实验平台的实验数据,该平台安装了一套双向通信无线模块用于平台与地面站的数据传输.
高压输电线路走廊内接近线路安全距离范围内的树障每年都会进行清理.经过统计分析,新长出的树障直径一般不会大于35 mm.故本文设计的树障清理机器人作业工具是根据35 mm以下的枝干切割能力设计的.为了留有设计余量,在本文设计的树障清理实验中,让机器人对一条直径约45 mm的树干进行切割,以进一步挖掘机器人和控制算法的潜能.在实验场地模拟输电线路走廊场景布置了机器人和被清障对象.实验过程如图12所示,它展示了树障清理空中机器人在从平飞状态到切割完成过程中的代表性动作节点.同时通过无线通信模块,本文获取了空中机器人的姿态角数据,并在图13中可视化了机器人在切割前后一个时间段内的俯仰、滚转和偏航角数据.此外图14给出了作业空中机器人在作业时间段由扩张状态观测器实时估计的姿态通道总扰动数据.
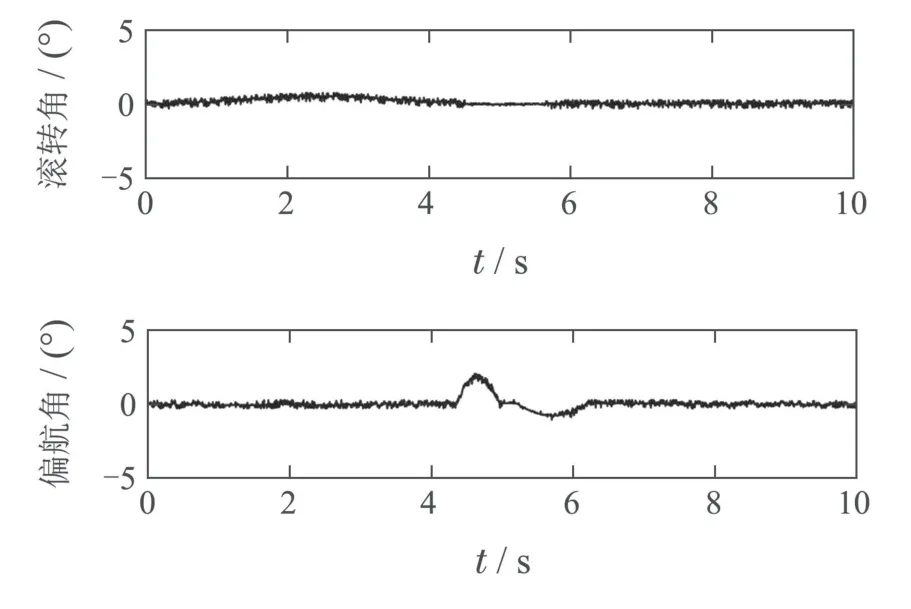
图13 空中机器人作业过程的姿态角数据Fig.13 Attitude angles of the aerial robot during operation
图12(a)中展示了作业型空中机器人作业前的平飞状态,图12(b)展示了机器人正在进行切割作业,该过程中姿态保持平稳,切割作用力的干扰环境下机器人抗扰能力较为理想,图12(c)展示了机器人完成切割的瞬间,锯片以上的树障段与下段分离,倒向前方并自行落向地面,图12(d)展示了此时机器人在突然失去切割接触力后姿态仍然能保持良好的稳定,说明了空中机器人具有不错的抗扰能力.

图12 空中机器人作业过程Fig.12 The operation process of the aerial robot
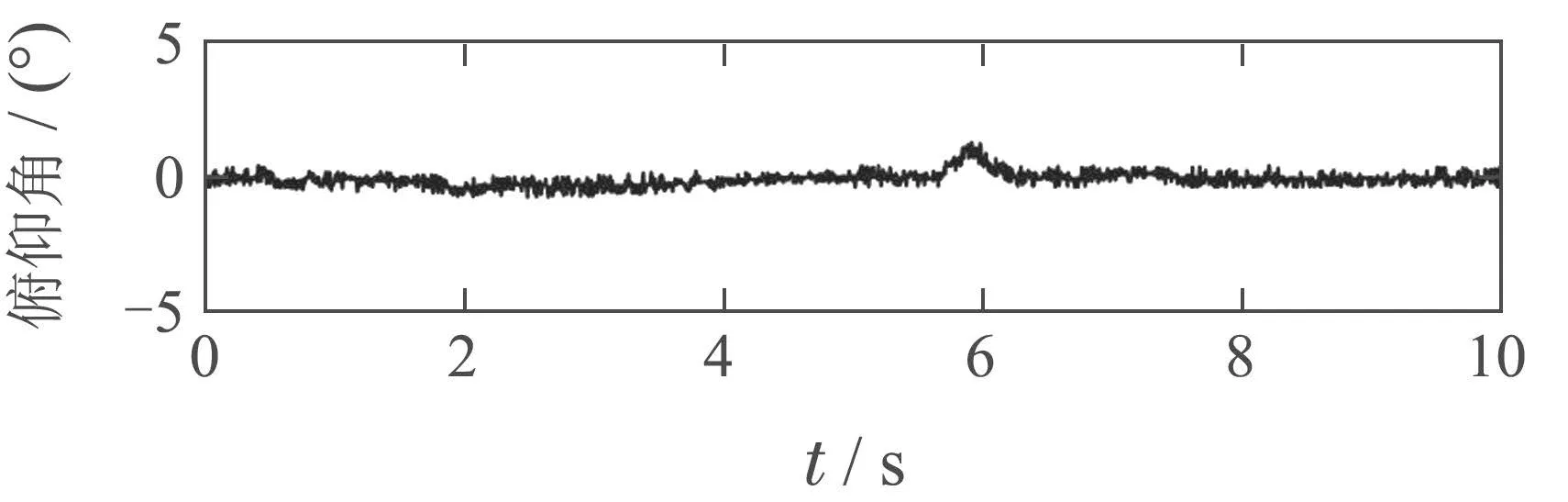
图13中可以发现机器人前进过程中俯仰角始终很小,与第5.1节仿真3中的平动性结果是一致的.
首先手动起飞空中机器人,将其飞行至被清理树障的后方3 m处,开启轨迹跟踪模式,让机器人跟踪轨迹前进并经过切割作业点.从图12-13可以看出,物理样机在自抗扰控制算法的作用下,较为平稳地完成了树障清理任务.得益于其推进器的设计,空中机器人接触树干之前可处于无俯仰角的前进平飞状态,从而实现了“零俯仰前进”的设计目的.空中机器人在4.4 s时刻开始接触待清理的树障,5.7 s 时完成清理,切断的树干自动掉落,此刻俯仰角和偏航角都产生了一定的波动,但自抗扰控制算法实时通过各姿态通道的扩张观测器估计总扰动值(如图14所示),积极地进行了控制补偿,迅速地指令机器人将姿态调整回稳定状态.
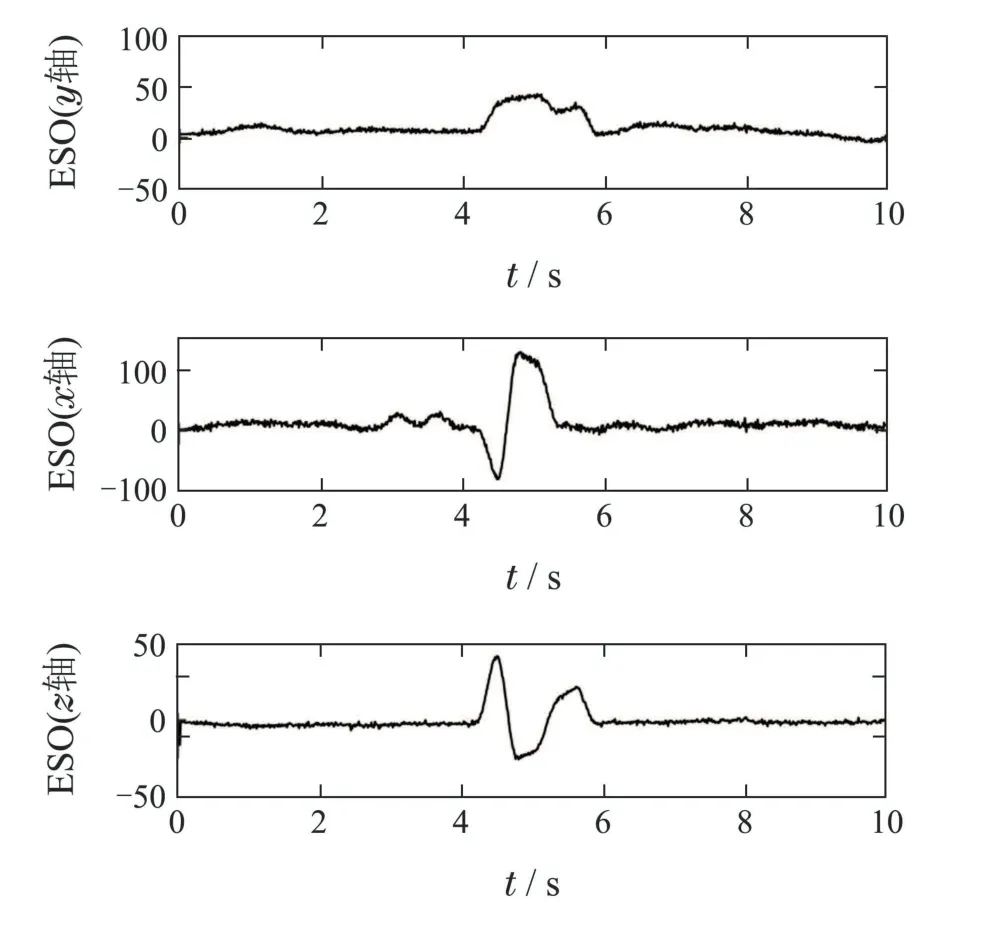
图14 机器人作业过程各通道扰动估计值Fig.14 Estimated values of disturbances in each channel during the robot operation
此外,从滚转角数据中可以发现,切割过程中树障清理空中机器人的滚转角波动减小,这较好地反映了作业锯片被树木夹持过程中空中机器人不易滚转的事实.图15-16分别表示机器人作业过程的位置、速度数据.图17表示机器人作业过程中的旋翼转速数据.物理实验中,外界扰动和系统不确定性因素更多,同时传感器也具有一定的误差,但从采集的数据中可以看出位置跟踪整体有效.
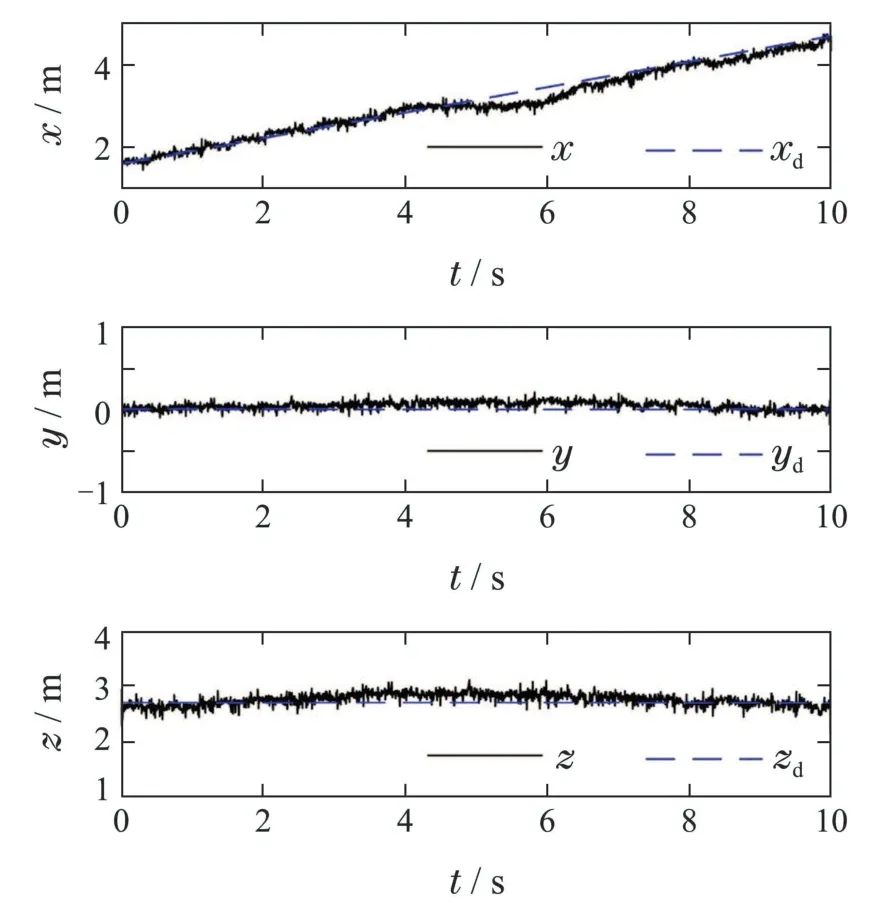
图15 机器人作业过程位置数据Fig.15 Robot position data during robot operation
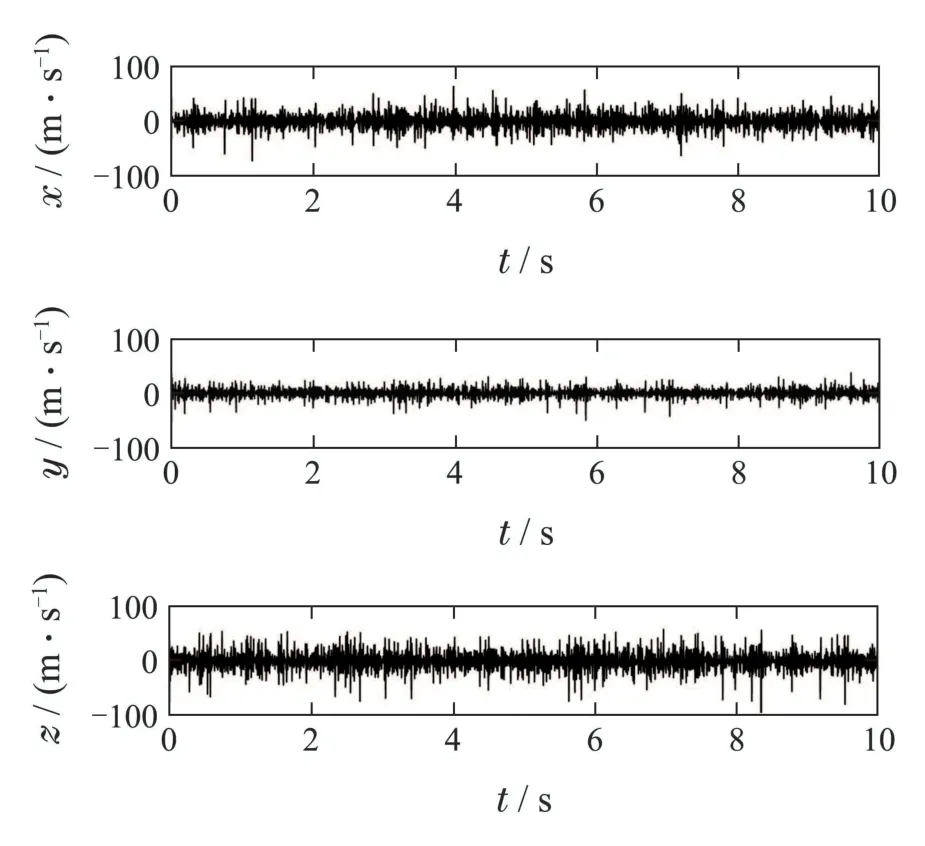
图16 机器人作业过程中速度数据Fig.16 Robot position speed data during robot operation
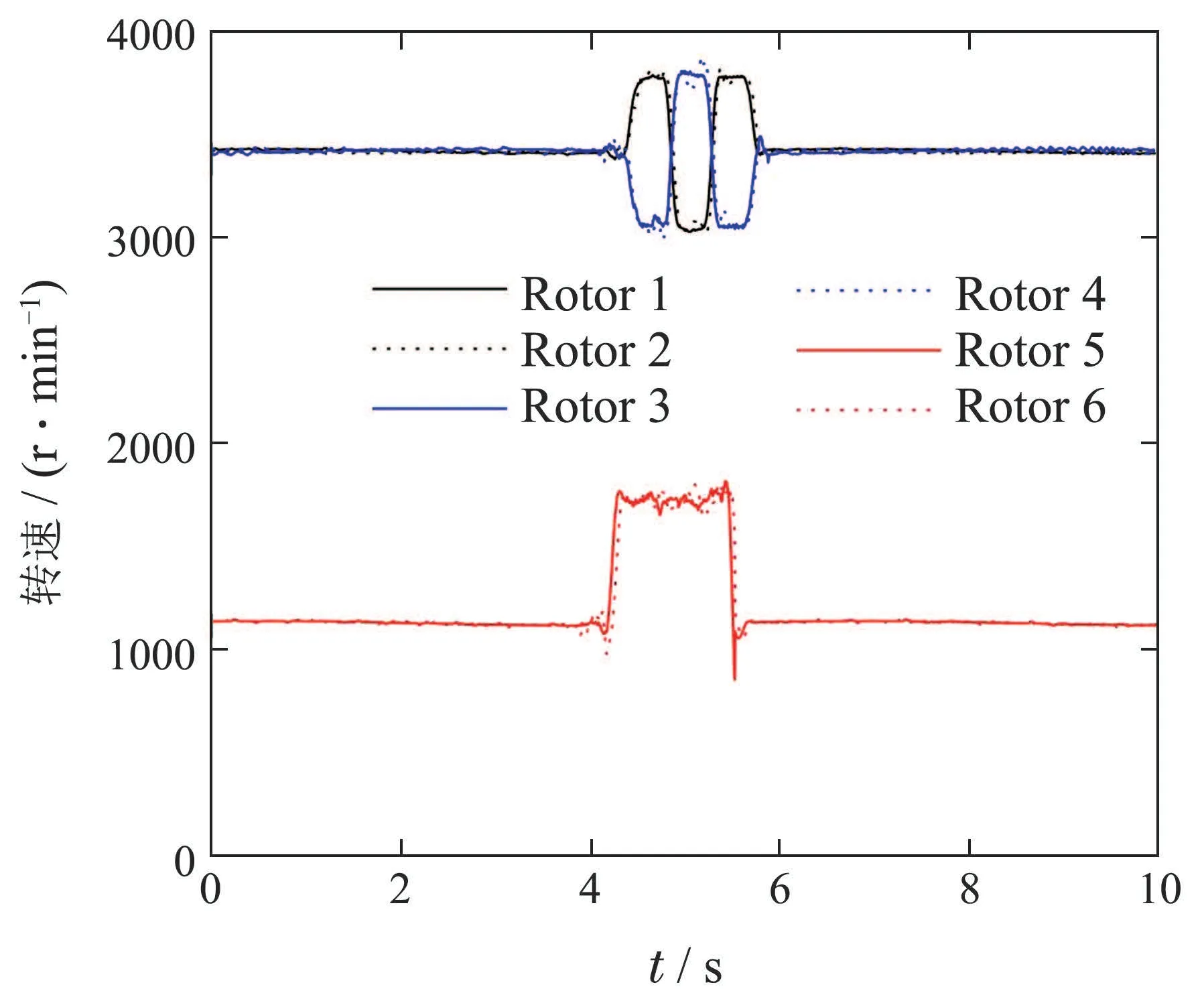
图17 机器人作业过程中的旋翼转速数据(控制输入)Fig.17 Rotors speed data during robot operation (control input)
样机实验结果表明,本文所设计的非平面配置旋翼空中机器人在自抗扰控制律作用下具有良好平动性和抗扰性.
6 结论
本文根据树障清理任务的实际工程需要,提出并设计了一种贴近工程需要的多旋翼空中机器人飞行平台,并为其设计了切实有效的控制分配方式和自抗扰飞行控制律,仿真和物理样机实验结果说明了该空中机器人构型能够满足工程需要,并且所设计自抗扰控制律能够较好地观测并抑制内外总扰动.
本文的研究也验证了非平面多旋翼空中机器人具有较大的内力作用的结论,并且更为直观地说明了采用具有观测器的控制方法进行这类多旋翼空中机器人飞行控制律设计的合理性和必要性.例如:飞行平台产生水平推力的同时也带来了较大的扭矩,对姿态控制产生一定影响,对于不具有观测器的控制律,需要在计算控制量的同时,根据模型给出的方程关系提前对该扭矩进行补偿,增加了控制律的复杂程度和不确定因素.
